文章信息
- 许志华, 吴立新, 刘军, 沈永林, 李发帅, 王然
- XU Zhihua, WU Lixin, LIU Jun, SHEN Yonglin, LI Fashuai, WANG Ran
- 顾及影像拓扑的SfM算法改进及其在灾场三维重建中的应用
- Modification of SfM Algorithm Referring to Image Topology and Its Application in 3-Dimension Reconstruction of Disaster Area
- 武汉大学学报·信息科学版, 2015, 40(5): 599-606
- Geomatics and Information Science of Wuhan University, 2015, 40(5): 599-606
- http://dx.doi.org/10.13203/j.whugis20130444
-
文章历史
- 收稿日期:2013-08-29
2. 中国矿业大学环境与测绘学院, 江苏 徐州, 221116;
3. 中国矿业大学(北京)地球科学与测绘工程学院, 北京, 100083
2. School of Environment Science & Spatial Informatics, China University of Mining and Technology, Xuzhou 221116, China;
3. School of Earth Science and Surveying Engineering, China University of Mining and Technology (Beijing), Beijing 100083, China
近年来,我国重大自然灾害多发、频发,给人民生命财产造成重大损失。低空无人机(unmanned aviation vehicle,UAV)遥感平台具备成本低、机动性强等优势,可快速获取高分辨率遥感影像[1, 2],已成为灾害监测与灾情评估的关键手段[3]。然而,目前UAV搭载光学传感器多用于环境监测与灾害调查[4, 5],在灾害立体测量方面研究较少,传统航空摄影测量理论与方法[6]的应急时效性和机动性不足。为克服现有灾害监测技术数据获取难、后处理时效性低等问题,亟需寻求新的灾害应急监测技术与数据处理方法。
基于视觉的三维重建技术不受物体形状限制,可实现全自动或半自动建模,已成为立体测量的重要研究方向。文献[7]全面介绍了基于视觉三维重建的主要方法及研究现状。分析结果表明,单目视觉方法可采用单视点或多视点的图像进行三维重建,对设备要求简单,成本低,易于实现,具有广阔的应用前景。其中,基于单视点的重建方法,如明暗度法[8]、光度立体视觉法[9]、纹理法[10]、轮廓法[11]等主要通过图像的二维特征(明暗度、纹理、轮廓等)推导出深度信息。该类方法复杂度低,可满足实时重建要求,但均依赖假设条件,通用性差,且受外界条件(如光照、纹理等)的影响,重建效果不稳定;而基于多视点的运动恢复结构(structure from motion,SfM)算法[12],主要利用一系列相互重叠的影像集,通过特征匹配来恢复相机的姿态参数及三维几何信息。该算法在重建过程中可实现相机的自标定,对影像要求低,且不依赖于特定的假设条件,通用性好,目前已得到广泛应用[13, 14, 15, 16]。文献[15]利用固定翼UAV影像和飞控数据,采用SfM算法构建了无地面控制点条件下三维坐标的解算模型,并验证了该模型应用于灾情评估的精度可靠性;文献[16]利用微旋翼UAV搭载数码相机获取滑坡影像,并采用SfM算法生成DEM来监测滑坡移动。但是,SfM算法在特征匹配阶段,目标影像需遍历全局待匹配影像,耗时多,重建效率低,影响了其在灾场快速三维重建方面的实际应用。文献[17]采用图论改进了SfM算法,通过建立匹配影像集的骨架,实现了一日罗马影像重建,但该方法并未减少影像遍历匹配的冗余判断;文献[18]采用GPU并行技术提出了VisualSFM算法,可大幅提高影像三维重建的效率,但该算法在读取高分辨率UAV影像时常需进行降采样处理,易造成信息丢失。此外,针对UAV序列影像,该算法的匹配效率尚有提高空间。
针对上述问题,本文利用UAV飞控系统提供的UAV运动位置、飞行姿态及相机参数信息来判断影像之间的重叠关系,建立影像拓扑关联关系,构建影像匹配索引表,改进SfM算法,通过约束参与特征匹配的影像搜索范围来提升三维重建效率。
1 拓扑-运动恢复结构算法
本文提出的拓扑-运动恢复结构(topology-based SfM,TSfM)算法主要包括分块特征提取、影像拓扑分析、特征匹配及运动恢复结构4个步骤。
1.1 分块特征提取
本文采用SIFT算法[19]提取UAV影像特征点。由于SIFT算法主要针对低分辨、小幅影像,在实际处理高分辨率UAV影像时易出现计算机内存溢出等问题。因此,本文针对UAV影像空间分辨率高、重叠度大的特点,采用影像分块策略的SIFT算法[15]来提取影像特征点。其主要思路为:先将原始影像分成大小相同的图块,分别对影像块依次建立尺度空间,检测极值点,生成特征描述符,并保存子块特征点文件;然后对子块进行合并,将特征点位置转换到原始影像范围内。此外,为确保在图块交界处检测到SIFT特征点,避免特征信息丢失,相邻图块之间需保持一定的重叠度。
1.2 影像拓扑分析
拓扑关系是明确定义空间关系的一种数学方法,常被用来描述并确定空间点、线、面之间的关系及属性,以实现相关的查询和检索。在地理信息系统中,影像拓扑关系属于简单面目标之间的拓扑关系,主要有相离、相接、交叠、相等、覆盖、包含、覆盖于、包含于等。
1) 飞控数据转换。UAV搭载飞控系统,可直接获取摄影曝光时刻影像的空间位置和姿态信息[15]。其中,飞控系统记录的传感器姿态角为IMU本体坐标系在导航坐标系中的侧滚、俯仰和偏航 (Φ,Θ,Ψ),通过5步坐标变换[20]得到地摄坐标系相对于像空间坐标系的外方位角元素(ψ,ω,κ)。
2) 计算影像角点坐标。以某拍照时刻飞机位置在地面的投影作为原点,以飞行航向为X轴,垂直X轴向右为Y轴,大地高方向为Z轴建立地摄坐标系。利用共线方程计算每张影像4个角点的地摄坐标值,则影像集用角点坐标表示为:

其中,n为影像数;Vij表示第i张影像的第j个角点坐标。
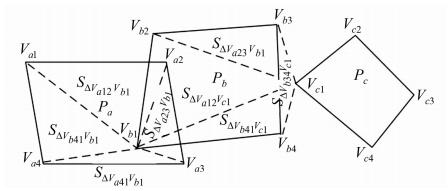
3) 面-点拓扑(包含)分析。利用计算机图形学理论分析影像(面)与其他影像角点(点)的“包含”关系(见式(2))。如图 1所示,T(Pa,Vb1)=1,T(Pb,Vc1)=0。
|
| 图 1 影像拓扑分析示意图 Fig. 1 Diagram of Image Topology Analyzing |
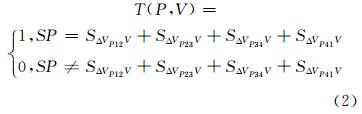
其中,T(P,V)=1为面P与点V的“包含”关系;T(P,V)=0为面P与点V的“非包含”关系。
4) 面-面拓扑分析。面由点顺序连接而成,因此,面-面拓扑关系可依据该面与其他面的角点拓扑关系进行分析。将面-点的“非包含”关系等价为影像间的“非关联”关系,即拓扑相离;将面-点“包含”关系等价为影像间的“关联”关系,即相接、交叠、相等、覆盖、包含、覆盖于、包含于等。据此,影像间的拓扑关系为:
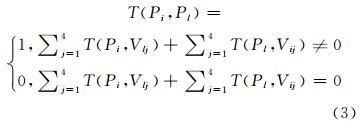
其中,T(Pi,Pl)=1为影像Pi与影像Pl的“关联”关系;T(Pi,Pl)=0为影像Pi与影像Pl的“非关联”关系。如图 1所示,T(Pa,Pb)=1,T(Pb,Pc)=0。
5) 构建影像拓扑关系图。依次判断全体影像之间的拓扑关系,将影像集抽象为点集V′(G),影像间的“关联”关系抽象为边集E(G),构建影像拓扑图为:
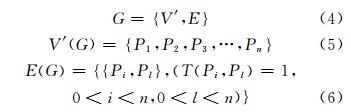
首先,根据目标影像Pm按边集拓扑图E(G)搜索其待匹配影像集TG,用点集图表示为V′(TG)={P1,P2,P3,…,Pm-1},确定其拓扑“关联”影像边集E(TG)={{Pi,Pm},T(Pi,Pm)=1,0<i
其中,fm和fn分别为目标影像Pm和待匹配影像集 TG中的特征点。
最后,采用随机抽取一致性(random sample consensus,RANSAC)策略[21]和8点算法[22]相结合,剔除误匹配点,建立满足对极几何约束[23]的精匹配特征点对集。
设参与匹配的所有影像中,影像的最大关联影像数为 k。最坏情况下,当待匹配的影像数小于k时,认为待匹配的影像全都参与匹配;当待匹配的影像数大于k时,则令实际参与匹配的影像数等于该目标影像的关联影像数(最坏情况下,认为目标影像的关联影像数均为k)。则影像匹配算法的时间复杂度为O(n),公式化表达为:
其中,n为重建影像总数;k为所有重建影像中影像的最大拓扑关联数(常数,且k
设相机参数为C={C1,C2,…Cn},点云坐标为p={p1,p2,…pt}。采用透视投影,将点云坐标投影到像平面坐标系,投影误差为g(C,p)。
其中,n为相机拍摄点位数(即影像总数);t为精匹配特征点个数;若点f在影像i上,ωi,f =1,否则ωi,f =0;||qi,f-r(Ci,pf)||2为点f在相机i投影面上的投影误差。
采用通用稀疏光束法平差(sparse bundler adjustment)[24]逐步迭代,使投影点和观测图像点之间的重投影误差最小,最终解算出相机位置、姿态以及精匹配特征点的三维坐标。
2 算法测试
2.1 测试数据
测试数据来源于山东省临沂市罗庄区(见图 2),该区域地形起伏,因建筑施工多处发生小面积滑坡。实验区航拍采用小型固定翼UAV,搭载传感器为松下DMC-FX75,预设飞行高程195 m,南北飞行4条航带,共56幅影像,影像大小为4 320像素×3 240 像素,影像分辨率约4 cm×4 cm,航拍面积约500×200 m2,航向重叠为90%,旁向重叠为60%。作业时5级风速、多云,飞行不稳,航线不规则。在实验区内均匀布设了7个十字形地面标示点(规格为9 cm×26 cm),并采用GPS RTK(灵锐S86)进行标示点坐标量测,作为后续模型精度评估的控制点。
本文采用TSfM算法对实验区的UAV序列影像进行拓扑分析、特征匹配和三维重建,并与SfM算法对比,分析匹配效率、重建效果及模型精度。
2.2.1 影像拓扑分析
图 3为对航拍影像进行相对定向并转换到地摄坐标系后生成的空间分布图,可见该航线受风影响,导致拍摄角度变化较大,难以通过预设航线判断影像拓扑关系。图 4为依据影像覆盖范围将影像抽象为点,将影像对的“关联”关系抽象为边而建立的影像拓扑关联关系图,表达影像匹配的索引关系。
TSfM算法中参与特征匹配的影像总次数等于有“关联”关系的影像对数目,共310次;而SfM算法采用全局匹配策略,匹配总次数 N=1+2+…+n-1=n×(n-1)/2=1 540次(n=56)。 可见,TSfM算法大幅减少了影像匹配的次数。参与匹配的影像数越多,TSfM算法的效率优势越明显。
2.2.3 算法效率分析
为测试TSfM算法的效率,本文将TSfM算法与SfM算法进行了对比,分阶段测试了特征提取、特征匹配和恢复重建的耗时情况(测试平台为PC,Intel(R) Core(TM)2 Duo CPU,内存2 G,Windows 32位操作系统),结果如表 1所示。其中,为避免处理高分辨率UAV影像出现计算机内存溢出,特征提取阶段均采用分块SIFT算法。结果表明,在影像三维重建过程中,两种算法在影像匹配阶段的耗时均较显著,而在恢复重建阶段耗时 均较少。但是,TSfM算法的匹配效率相对于SfM算法有大幅提高,匹配耗时由8.632 h减少至0.788 h(见表 1),三维重建总耗时减少近8 h,效率提高7倍以上。
图 5为SfM算法和TSfM算法进行单张影像特征匹配的耗时曲线。可见,SfM算法单张影像的匹配耗时在整体上随影像序号的增加呈线性增长趋势,这是由于随着影像序号增加,该影像需遍历的待匹配影像数增多,导致特征点间的冗余匹配次数增加,进而增加匹配耗时;而TSfM算法参与特征匹配的影像数量只与该影像“关联”的影像数有关。图 5中红圈、蓝圈所示影像出现了特征匹配耗时异常,是因为影像地物的复杂性不同及影像与待匹配影像的“关联”影像数不同所致。一般地,影像地物愈复杂,所提取的特征点数愈多;影像与待匹配影像的“关联”拓扑关系数愈多,匹配耗时愈长。
为测试三维重建效果,本文分别对TSfM与SfM算法的三维重建点云进行了对比分析。图 6(a)、6(b)分别为采用SfM算法和TSfM算法重建的三维点云,重建结果均完整保持了实验区域的三维形态。但是,TSfM算法在重建点云数量上相对于SfM算法略有减少(由55 300减少为49 272),所减少的点主要集中在边缘区域(图 6(a)红圈标示)。这是由于在航线的拐点飞机姿态瞬间变化较大(偏航角变化近±180°),致使飞控记录数据误差偏大,部分影像关联拓扑漏判,实际参与匹配的影像数偏少。因此,设置航线时,增大UAV在拐点处的飞行半径,可在一定程度上减小飞控系统的记录误差,从而减小影像关联拓扑的漏判率。
利用飞控数据对点云进行地理注册,将点云转换到WGS-84坐标系。选取均匀布设在实验区的7个地面控制点进行误差分析。
由于灾情应急测量主要侧重于灾情信息获取,相对于灾损地物的绝对位置,灾损对象之间的相对位置及空间关系更为重要[15]。因此,本文重点关注模型的相对误差,通过比较控制点间的相对长度误差(即计算长度与实际长度之差与实际长度的比值)可知,TSfM算法重建模型的相对精度优于4.4%(见图 7),可满足灾害应急条件下灾情评估的需求。
此外,本文也对SfM算法和TSfM算法重建模型的相对精度进行了对比,揭示两者重建模型的相对精度高度一致,表明TSfM算法中引入影像拓扑分析后,减少匹配次数、大幅提高影像匹配效率的同时,并没有损失重建精度。
3 四川芦山地震灾区重建应用
3.1 数据介绍
2013-04-20T08:02,四川省雅安市芦山县(30.3°N,103.0°E)发生Ms 7.0级地震,震源深度13 km。地震发生后,中国科学院遥感与数字地球研究所与中国人民财产保险股份有限公司合作,于2013-04-22下午,利用固定翼UAV对地震重灾区芦山县进行航拍。航拍范围为芦山县太平镇重灾区,作业时3级微风、多云,飞行稳定,平均相对高度500 m,传感器为佳能EOS 5D MarkⅡ数码相机,焦距35 mm,共4条航带,共拍摄187张影像,影像大小为5 616像素×3 744像素,影像分辨率约9 cm×9 cm,航向重叠度为80%,旁向重叠度为60%。
3.2 灾场重建与灾情检测
图 8为采用TSfM算法得到的太平镇重灾区的三维点云。重建结果保持了灾损地物间的空间分布格局,可用于灾情检测与评估[25]。图 8中红框标示区域所示为检测到的3处山体滑坡。
为评估滑坡灾情的影响范围,作者分别利用重建的点云和UAV航拍影像对检测到的3处滑坡体做了对比分析。图 9(a)、图 9(b)分别为利用三维点云(俯视)和UAV航拍影像检测到的山体滑坡(LS1、LS2和LS3)。从空间分布上判断,LS2特征明显、影响范围较大,已造成道路封堵。图 9(c)为利用三维点云生成的滑坡体DSM(点云经地理注册,已转换到用户坐标系),反映了滑坡体分布的三维形态,有助于灾情分析与评估。如LS1红圈标示处局部高程变化明显,且地势较高,为一处新生断崖,推测为大块岩体坍塌所致,尚有潜在滑动危险;LS2黑圈标示处地势较低,且局部高程增大,检测为因岩体滑落导致大量岩体堆积,并有进一步扩大的趋势。
表 2为分别采用UAV航拍影像和三维点云对滑坡灾情定量评估的结果。结果显示,UAV航拍影像评估滑坡体LS1、LS2和LS3的面积分别为417.73 m2、3 443.18 m2和457.12 m2,均小于点云评估结果的826.84 m2、3 993.35 m2和562.76 m2。分析其原因,采用点云评估得到的是滑坡体的表面积,而UAV影像检测的结果是滑坡体的投影面积。显然,利用点云得到的表面积更能体现滑坡体的地形起伏情况,评估结果更准确。此外,本文还利用三维点云评估了3处滑坡体的方量分别为1 613.09 m3、13 453.53 m3和707.40 m3,可为灾情救援提供更可靠的保障。
为进一步验证TSfM算法的高效性,本文同时对芦山震区187张影像进行了效率测试,结果见表 1。可见,影像匹配阶段仍耗时最多,但其占重建总耗时的比重较测试数据的结果明显减少,如SfM算法的匹配耗时比重为0.64(2.861/4.461)小于测试数据的0.95(8.632/9.063)。其主要原因为,芦山震区数据分辨率相对较低,约为9 cm×9 cm,且地物单一,多为植被,细节特征变化较小,导致影像中提取的特征点数(约103/张)远小于测试数据中提取的特征点数(约104/张),单张影像特征匹配次数减少。
尽管如此,TSfM算法的匹配效率相对于SfM算法仍有大幅提高,匹配耗时由2.861 h减少至0.842 h,与参与匹配的影像数成正相关,由17 391次减少至4 975次,效率提升约2.5倍。
4 结 语
本文提出了一种利用影像拓扑关系改进SfM的快速三维重建方法(TSfM)。TSfM方法利用UAV飞控数据来建立影像的拓扑关联关系,并据此来约束特征相似度判断的影像搜索范围,进而构造出基于影像拓扑关联关系的特征匹配模型,减少了匹配次数,简化了影像匹配的算法复杂度。滑坡区UAV影像三维重建实验及对比分析表明,TSfM算法在大幅提高影像匹配效率的同时并不损失重建精度,可服务于灾场快速三维重建。
由芦山地震灾情UAV影像三维重建应用可知,三维重建点云相比二维影像在灾损目标识别、评估灾损量等方面具有明显优势。为进一步提升TSfM算法的能力与可靠性,下一步将借助局部特征相似判断(如色差、直方图核函数等)来约束特征提取的条件,保证影像提取的特征点均匀、可靠,进一步提高匹配效率。此外,在恢复重建阶段,参与重建的影像顺序依赖于匹配特征点的数量,始于精匹配点最多的匹配影像对,并依据其影像连接关系添加影像,从而忽略了影像本身覆盖范围的重要性。因此,如何利用影像拓扑关系来判断影像的重要性,进而指导恢复重建,也是下一步研究的重点。
致谢:中国人民财产保险公司灾害研究中心王平副总经理的帮助及中国科学院遥感与数字地球研究所刘纯波副研究员提供的芦山地震UAV影像。
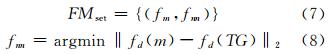
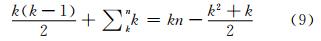
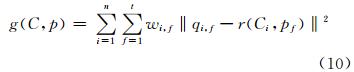

图 2 实验测试区
Fig. 2 UAV Panoramic Image of the Experimental Area
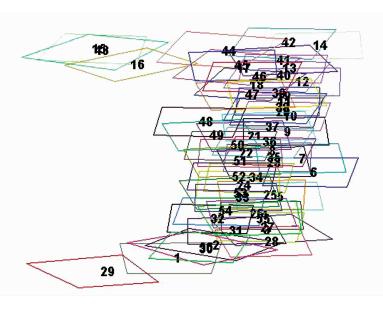
图 3 测试航拍影像的空间分布图
Fig. 3 Spatial Coverage of Experimental Images
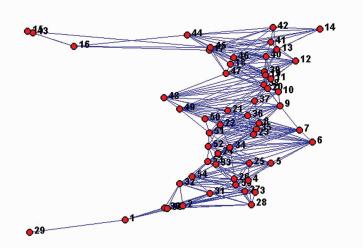
图 4 航拍影像集的拓扑关联关系图
Fig. 4 Topological Conjunction Graph of
the UAV Images
算法耗时
测试数据 芦山震区数据
SfM TSfM SfM TSfM
特征提取
0.409
0.409
0.950
0.950
特征匹配
8.632
0.778
2.861
0.842
恢复重建
0.022
0.021
0.650
0.600
总耗时
9.063
1.208
4.461
2.392
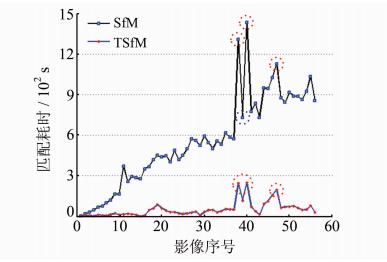
图 5 单张影像特征匹配耗时对比
Fig. 5 Matching Efficiency Comparison on Single Image
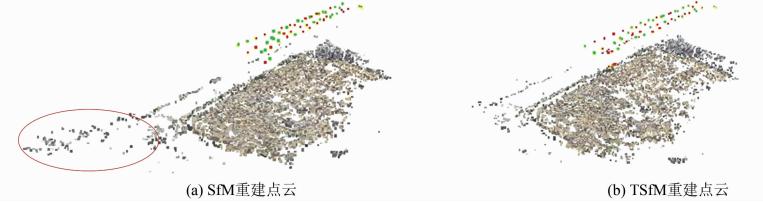
图 6 SfM与TSfM算法三维重建结果对比
Fig. 6 3D Reconstruction Results Comparison from SfM and TSfM Algorithms
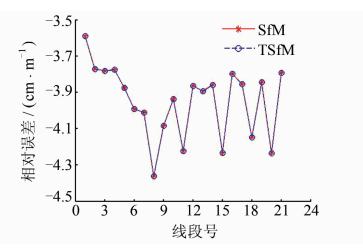
图 7 重建模型的相对精度对比
Fig. 7 Relative Accuracy Comparison on Models
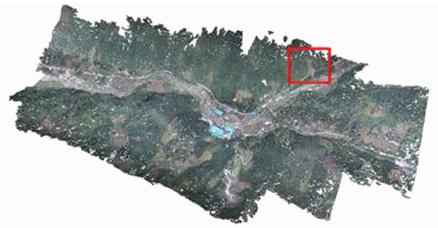
图 8 太平镇地震灾区三维重建结果
Fig. 8 3D Reconstruction of Earthquake-Stricken
in Taiping Town
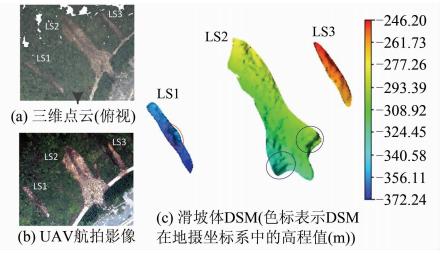
图 9 滑坡检测结果
Fig. 9 Landslide Motoring Results
UAV影像 三维点云
面积/m2 表面积/m2 方量/m3
LS1
417.73
826.84
1 613.09
LS2
3443.18
3 993.35
13 453.53
LS3
457.12
562.76
707.40
| [1] | Yan Lei, Lu Shuqiang, Zhao Hongying, et al. Research on Key Techniques of Aerial Remote Sensing System for Unmanned Aerial Vehicles[J]. Engineering Journal of Wuhan University, 2004, 37(6): 67-71(晏磊, 吕书强, 赵红颖, 等. 无人机航空遥感系统关键技术研究[J]. 武汉大学学报(工学版), 2004, 37(6): 67-71) |
| [2] | Zang Ke, Sun Yonghua, Li Jing, et al. Application of Miniature Unmanned Aerial Vehicle Remote Sensing System to Wenchuan Earthquake[J]. Journal of Natural Disasters, 2010, 19(3): 162-166(臧克,孙永华, 李京, 等. 微型无人机遥感系统在汶川地震中的应用[J].自然灾害学报, 2010, 19(3): 162-166) |
| [3] | Niethammer U, James M R,Rothmund S,et al.UAV-Based Remote Sensing of the Super-Sauze Landslide: Evaluation and Results[J]. Engineering Geology, 2012, 128(1):2-11 |
| [4] | Douterloigne K,Gautama S,Philips W,et al.On the Accuracy of 3D Landscapes from UAV Image Data[C]. IGARSS, Honolulu, Hawaii, USA, 2010 |
| [5] | Gademer A, Petipas B, Mobaied S, et al. Developing a Lowcost Vertical Take off and Landing Unmanned Aerial System for Centimetric Monitoring of Biodiversity the Fontainebleau Forest Case[C]. IGARSS, Honolulu, Hawaii, USA, 2010 |
| [6] | Xiang H T, Lei T, Method for AutomaticGeoreferencing Aerial Remote Sensing Images from an Unmanned Aerial Vehicle (UAV) Platform[J]. Biosystem Engineering, 2011, 108(2): 104-113 |
| [7] | Tong Shuai, Xu Xiaogang, Yi Chengtao, et al. Overview on Vision-Based 3D Reconstruction[J]. Application Research of Computer, 2011, 28(7): 2 411-2 417(佟帅,徐晓刚,易成涛,等.基于视觉的三维技术综述[J]. 计算机应用研究. 2011, 28(7): 2 411-2 417 |
| [8] | Horn B. Shape from Shading: A Method for Obtaining the Shape of A Smooth Opaque Object from One View[D]. Cambridge: Cambridge University, 1970 |
| [9] | Woodham R J. Photometric Method for Determining Surface Orientation from Multiple images[J]. Optical Engineering, 1980, 19(1): 139-144 |
| [10] | Wiktin A. Recovering Surface Shape and Orientation from Texture[J]. Artificial Intelligence, 1981, 17(1-3): 17-45 |
| [11] | Martin W N, Aggarwal J K. Volumetric Descriptions of Objects from Multiple Views[J]. IEEE Trans on PAMI, 1983, 5(2): 150-158 |
| [12] | Snavely N. Scene Reconstruction and Visualization from Internet Photo Collections [D]. Washington: University of Washington, 2008 |
| [13] | Niethammer U, Rothmund S. UAV-Based Remote Sensing of Landslides[C]. International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences Symposium, Newcastle Upon Tyne, UK, 2010 |
| [14] | Rosnell T, Honkavaara E. Point Cloud Generation from Aerial Image Data Acquired by a Quadrocopter Type Micro Unmanned Aerial Vehicle and a Digital Still Camera[J]. Sensors, 2012, 12: 453-480 |
| [15] | Shen Yonglin, Liu Jun, Wu Lixin, et al. Reconstruction of Disaster Scene from UAV Images and Flight-Control Data[J]. Geography and Geo-Information Science, 2011, 27(6): 13-17(沈永林, 刘军, 吴立新, 等.基于无人机影像和飞控数据的灾场重建方法研究[J]. 地理与地理信息科学, 2011, 27(6): 13-17) |
| [16] | Turner D, Lucieer A. Using a Micro Unmanned Aerial Vehicle (UAV) for Ultra High Resolution Mapping and Monitoring of Landslide Dynamics[C]. IGARSS, Melbourne, Austrilia, 2013 |
| [17] | Agarwal S, Snavely N, Simon I, et al. Building Rome in a Day[C]. ICCV, Kyoto, Japan, 2009 |
| [18] | Wu C. Towards Linear-Time Incremental Structure from Motion[C]. 3DV, Seattle, WA, USA, 2013 |
| [19] | Lowe D. Distinctive Image Features from Scale-Invariant Keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91-110 |
| [20] | Liu Jun, Zhang Yongsheng, Wang Donghong, et al. Computing Method of Exterior Orientation Elements of POS AV 510-DC System[J]. Geomatics Technology and Equipment, 2004, 6(4): 43-47(刘 军, 张永生, 王冬红, 等. POS AV510-DG 系统外方位元素的计算方法[J]. 测绘技术装备, 2004, 6(4): 43-47) |
| [21] | Fischler M A,Bolles R C.Random Sample Consensus:A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography[J]. Communications of the ACM,1981, 24(6): 381-395 |
| [22] | Hartley R I. In Defense of the Eight-Point Algorithm[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1997, 19(6): 580-593 |
| [23] | Hartley R, Zisserman A. Multiple View Geometry in Computer Vision[M]. Cambridge, UK: Cambridge University Press, 2000 |
| [24] | Lourakis M, Argyros A. The Design and Implementation of a Generic Sparse Bundle Adjustment Software Package Based on the Levenberg-Marquardt Algorithm[R]. Technical Report 340, Inst.of Computer Science-FORTH, Heraklion, Greece, 2004 |
| [25] | Xu Zhihua, Liu Chunbo, Wang Ping, et al. Airborne Union Observation and Disaster Enhanced Identification of Ms 7.0 Lushan Earthquake[J]. Science and Technology Review, 2013, 31(12): 37-41(许志华, 刘纯波, 王平, 等. 四川芦山Ms7.0级地震空基联合观测与灾情增强识别[J]. 科技导报, 2013, 31(12): 37-41) |
 2015, Vol. 40
2015, Vol. 40



