文章信息
- 马友青, 刘少创, 魏士俨, 李明磊
- MA Youqing, LIU Shaochuang, WEI Shiyan, LI Minglei
- 加权总体最小二乘的地面解析摄影测量算法
- Terrestrial Analytical Photogrammetry with Weighted Total Least Squares
- 武汉大学学报·信息科学版, 2015, 40(5): 594-598
- Geomatics and Information Science of Wuhan University, 2015, 40(5): 594-598
- http://dx.doi.org/10.13203/j.whugis20130387
-
文章历史
- 收稿日期:2013-08-06
2. 中国科学院遥感与数字地球研究所, 北京, 100101;
3. 国家海洋局第三海洋研究所, 福建 厦门, 361005
2. Institute of Remote Sensing and Digital Earth, Chinese Academy of Sciences, Beijing 100101, China;
3. Third Institute of Oceanography, State Oceanic Administration, Xiamen 361005, China
地面摄影测量是通过摄影测量的方法,对近距离目标的外形、形态和几何位置进行确定的技术。与传统摄影测量相比,主要区别为成像方式和平差模型。在成像方式上,传摄影测量像片的主光轴近似位于一个平面内,而且成像区域近似为同等分辨率下。例如,航空摄影测量中为等高度垂直地面成像,近景摄影测量中对大型建筑物的垂直目标物拍照等。而地面摄影测量成像时,摄影主光轴近似平行于地面,远处目标物的成像精度低,近处的精度高。在摄影测量平差模型的角度上,传统摄影测量广泛采用基于高斯马尔科夫模型(GM模型)的最小二乘平差(LS)解,但其前提是偶然误差只存在于观测向量中,系数矩阵不含有误差。然而在实际测量中,观测向量与系数矩阵均存在误差,需要建立更为合理的计算模型。
目前,在解析相对定向理论的拓展方面,文献[1]研究了近景摄影测量中的大角度问题,文献[2, 3]探讨了沿主光轴摄影相对定向、像点上下视差与影像外方位元素间的相关性。在总体最小二乘平差理论(TLS)与摄影测量学等领域,也取得了一些显著的理论成果。文献[4, 5]研究了基于约束条件的加权总体最小二乘(WTLS)方法,文献[6]将WTLS引入到相似变换模型中,文献[7]揭示了TLS与经典平差方法的关系,文献[8]研究了加权情况下附有相对权比的TLS方法,文献[9]将TLS引入到摄影测量学科中的空间后方交会模型。目前的研究成果尚未将TLS理论引入到解析相对定向模型中,基于解析绝对定向模型的TLS解仍需要进一步的探讨。因此,本文以解析相对定向、绝对定向模型为研究对象,尝试将加权总体最小二乘平差理论引入到地面摄影测量立体像对的处理中。
1 基于WTLS原理的相对定向 1.1 相对定向
相对定向是一种获取立体像片的相对方位元素值的解析方法。其基本模型有:连续相对定向和单模型相对定向。设像点上下视差为等权时,其误差方程式为:

各系数的具体表达式参见文献[10]。
在立体相机对地成像时,应用相对定向理论需要考虑远近目标的像点坐标观测权值和系数矩阵 A 的误差。因此,本文将WTLS理论[4]引入到近景摄影测量相对定向模型中,给出了式(1)的WTLS解步骤。
1.2 含误差变量模型的WTLS解
LS方法适用于无噪声系数矩阵、观测向量只包含随机误差的GM模型,依赖于参数的初始值。含误差变量模型[4](errors-in-variables,EIV)认为系数矩阵、观测向量均含有随机误差,采用TLS求解待定参数。在式(1)系数矩阵 A 中,包含了像点坐标观测量、像片内方位元素测量值以及立体模型摄影基线分量BX、BY、BZ,认为像片内方位元素和基线分量为伪随机观测量,因此,A 包含多种随机误差。将式(1)转换为EIV理论模型:
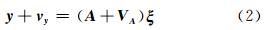
其中,vy为y的残差向量;VA为A 的残差矩阵; ξ 为待求参数向量(u×1);n为同名像点坐标观测的数目。方差模型为:

其中,l为包含A 、 y的扩展观测向量;σ02为中误差; Qll 、 P为其协因数矩阵和权矩阵; QAA 、 Qyy分别为 A和y 的协因数矩阵,QAy为A 、 y相关的协因数矩阵(QAy =Q yA T)。在实际计算中,忽略向量A 、 y的相互关系,将矩阵QAy 、 QyA元素均设为零,根据像点坐标精度给QAA 、 Qyy赋值。
拉格朗日法与奇异值分解是TLS的两种基本解法。设λ为拉格朗日乘积因子向量,则基于拉格朗日法的TLS解表达式[4]为:
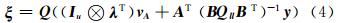
其中, 其中,Δ Pyy = Pyy ( Q -1+ Pyy )-1 Pyy 。在不考虑系数矩阵残差时,式(5)为零 ,即WLS和WTLS解是一致的。
本文采用拉格朗日法,则基于相对定向模型的WTLS迭代解步骤如下。
1) 匹配量测出同名像点,并对像点坐标进行系统误差处理,如相机物镜畸变的补偿。设定定向参数初始值。
2) 按照式(1)逐点计算定向点的上下视差并构建误差方程式。根据GM模型下的LS解,确定式(2) 中 ξ i(i=0)。
3) 根据式(4),确定参数向量 ξ i+1。
4) 若‖ ξ i+1- ξ i‖/‖ ξ i‖<ε不成立,则回归至步骤2;否则,将 ξ i+1确定为待定参数解。其中,ε为阈值,‖·‖表示L2范数。
与基于拉格朗日法的TLS迭代解不同,奇异值分解是一种直接解法[10]。在观测量等精度情况下,对式(2)的增广矩阵[A y]进行奇异值分解:
其中,Σ n×(m+1)=diag(σ1,σ2,…,σi),σi>0(i=1,2,…,m+1)且为[A y]的奇异值。根据文献[9],相对定向参数的表达式为:
其中,vm+1,m+1为矩阵 V 的最后一个元素;参数残差向量为
2 Procrustes理论的绝对定向
2.1 绝对定向
绝对定向实际上是三维相似变换问题,假设有n个空间点,在原坐标系统和目标坐标系统下均有坐标测量值,则有:
其中,1 n×1为元素为1的向量; A 、 Y 为空间点在原坐标系统、目标坐标系统下的坐标矩阵。 T 、λ为平移参数和比例系数; ξ 是由φ、ω、κ三个独立旋转角构成的旋转矩阵。由于 Y 、 A 均含有随机误差,因此依旧引入EIV模型。在参照相对定向模型的WTLS解时,需将绝对定向待求参数构建成单一向量,其系数矩阵表达式较为复杂。利用传统的LS对绝对定向模型进行解算时,误差方程式的系数矩阵也较为复杂,且依赖于待求参数的初始值[10]。由于Procrustes理论[5]在计算三维相似变换模型中具有计算稳定、不依赖于待定参数的初始值即可完成直接计算的特性,避免了单一利用WTLS算法或LS算法进行解算时误差方程式的建立和系数矩阵的复杂计算,因此,本文将Procrustes理论和WTLS解法同时引入到绝对定向模型中。
2.2 基于Procrustes理论的LS解
将式(8)变为 Y 1= Y 2 X3 Tx 1+ 1 x 2 T。其中,x1、 x2 、X 3依次为比例系数、平移向量和旋转矩阵。 Y 1、 Y 2为目标坐标系、原坐标系下的坐标观测量矩阵,设 Y 1残差为 E ,权阵 W =diag(w1,…,wn),则式(8)等同于:
LS解必须满足加权L2范数最小的条件:
令函数L(x1,x 2,X 3)=(1/2)‖ E ‖2。根据文献直接得到平移参数向量为:
比例系数为:
其中,C = I -( 1 T W1 )-1 11 T W 。将计算出来的x1、 x 2代入到L(x1,x 2,X 3),则有:
若使式(10)成立,需使L( X 3)最小,那么应确保式(13)等号右边的第二项最大,即满足分子tr( Y 1T C T WCY 2 X 3T)最大,其分母和等号右边的第一项均为常量。设 M = Y 1T C T WCY 2并对其进行奇异值分解 M = UΣV T,令 K = V T X 3T U ,根据矩阵迹运算的性质,则有:
其中,K =[kii],若 K = I ,那么式(14)等号成立,则有:
式(8)中,设 Y 、 A 的残差分别为 EY 、 EA 。在忽略 T 、λ的情况下将式(8)变换为等精度下的EIV模型:
文献[6]说明了旋转矩阵 ξ 的TLS解,与Procrustes理论下的LS解一致。
在考虑 T 、λ的情况下,设 A ′= A ξ ,再通过式(17)求解 λ[4]:
上述过程均认为观测量为等精度独立观测。在实际测量中,必须引入观测值权值。根据权值矩阵 W n与 残差矩阵逐行乘积的顺序,基于Procrustes理论的WTLS解应满足目标函数的最小化[6]:
并给出绝对定向的WTLS解步骤:
1) 用幂等重心矩阵 B = I n-( 1 nT W n2 1 n)-1·( 1 n 1 nT W n2),重心化 = W n BA ,= W n BY 。
2) 对 AT Y进行奇异值分解 ATY = UΣV T,根据式(15),可以计算出旋转矩阵 ξ = UDV T。一般地,D 为单位阵。
3) 解算式(17)并选择合理的解λ。计算 T =( 1 nT W n2 1 n)-1 1 nT W n2( Y -λ A ξ )。
3 实验与分析
3.1 相对定向算例
算例为地面摄影测量立体像对,左像片内方位元素为(1 194.737 像素,-6.263 像素,-10.715 像素),右像片内方位元素为(1 192.038 像素,-3.027 像素,-5.715 像素)。像点坐标总体量测精度为0.1 像素,且为不等精度独立观测。选择了3对均匀覆盖重叠区域的同名像点,进行了连续和单模型相对定向的最小二乘解 (LS解)、基于奇异值分解的TLS解(TLS解)以及加权总体最小二乘解(WTLS解),结果见表 1、2。
根据目标点距相机的距离与像点坐标精度的关系,近处的像点坐标上下视差观测值精度较高,远处的精度较低。因此,WTLS解中,在将像点坐标上下视差视为伪独立观测值时,其协因数矩阵 Qll 设计为对角阵diag(1,1,100,100,10 000,10 000),阈值ε设置为1.0×1010。 LS解和TLS解中,像点坐标假定为等精度观测,σ0为单位权中误差。
对比表 1、2中的第2~4列,3种解法的定向参数基本一致。表 1中的中误差分别为0.021 406像素、0.020 795 像素、0.013 244 像素,表 2中的中误差分别为0.341 602 像素、0.321 956像素、0.303 82 像素,均说明了WTLS的计算精度要高于LS解和TLS解。因此可引申出WTLS算法更适合地面摄影测量的相对定向模型。
3.2 绝对定向算例
为了验证本文提出的绝对定向模型解法,利用表 1中的同名像点坐标原始数据前方交会出目标点坐标,目标点所在的坐标系称之为原系统坐标系。用两台徕卡TS06全站仪通过前方交会法测量出该6个点在目标系统坐标系下的坐标,仪器的测角精度是2″,点位平面中误差为0.1 mm,高程中误差为0.07 mm。表 3给出了LS解、基于Procrustes算法的LS解(Procrustes解)以及基于Procrustes算法的TLS解(TLS解)和WTLS解的测试结果。
表 3中,LS解收敛次数为6,第2~4列中,假定坐标测量值均为等精度量测;第5列中,目标点坐标为不等精度观测,权值矩阵设计为diag(1.0 1.1 1.13 1.1 1.2 1.1)。
分析表 3中的第2~4行,平移参数ΔX、ΔY、ΔZ在Procrustes解下,其变化幅度为0.1 mm,而在LS解、TLS解以及WTLS解下基本一致,变化的幅度为0.01 mm,这说明比例系数影响了LS解和TLS解的一致性,导致了Procrustes解对计算结果的影响程度,表现为变化幅度较大。由于表 3中第4、5列均考虑了比例系数,减小了其对平移参数的影响,所以计算结果的变化幅度较小。
分析表 3中第5~8行,比例系数、旋转角基本一致。Procrustes解和TLS解均采用式(15)求解旋转角,故其完全相同。依据最后一行,σ0分别为11.592 88 mm、3.420 081 mm、3.113 425 mm和3.434 561 mm,WTLS解的精度最高。说明了相对于LS法,WTLS法在解算绝对定向模型时更为合理。
4 结 语
本文在进行解析相对定向和绝对定向的计算中,首次引入了WTLS和Procrustes理论。通过大量的实验分析,可得出如下结论。
1) 将WTLS算法引入到地面摄影测量解析相对定向中是可行的,且基于奇异值分解的WTLS算法在保证精度的同时,直接计算定向参数。
2) Procrustes理论的WTLS解法可作为地面摄影测量绝对定向模型的一种直接解法,不依赖于待求参数的初始值。
3) 将WTLS理论应用到地面摄影测量解析算法中,其精度和算法效率均高于常规GM模型下的LS解。
下一步的研究将继续拓展应用于相对定向模型的WTLS理论以及其与LS等经典平差方法的精度比较。
 表示Kronecker积; B n×n(u+1)=( ξ T
表示Kronecker积; B n×n(u+1)=( ξ T I n,- I n),I n为单位阵; Q =( A T( BQllB T)-1 A )-1; λ =( BQllBT)-1( y - Aξ ); v =[vA
I n,- I n),I n为单位阵; Q =( A T( BQllB T)-1 A )-1; λ =( BQllBT)-1( y - Aξ ); v =[vA  vy]T= QllB Tλ。 下文给出WTLS解和加权LS解(WLS)的理论联系:
vy]T= QllB Tλ。 下文给出WTLS解和加权LS解(WLS)的理论联系:
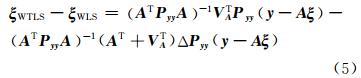

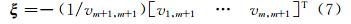
 。其中,vec(·)表示矩阵按行拉伸后的行向量。
。其中,vec(·)表示矩阵按行拉伸后的行向量。
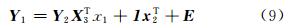
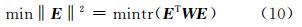
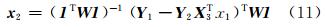
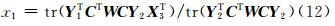
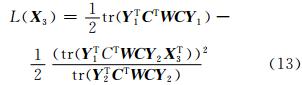
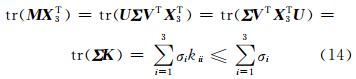

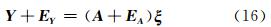

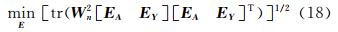
参数
算法
LS解 TLS解 WTLS解
μ/rad
-0.108 818
-0.099 079
-0.101 259
ν/rad
0.002 805
-0.007 604
-0.009 248
φ/rad
-0.005 429
-0.006 219
-0.004 523
ω/rad
-0.003 525
-0.004 886
-0.004 725
κ/rad
0.020 307
0.020 221
0.020 416
σ0/像素
0.021 406
0.020 795
0.013 244
参数
算法
LS解 TLS解 WTLS解
φ1/rad
-0.002 672
0.007 417
0.008 778
φ2/rad
-0.006 793
0.002 221
0.003 896
ω2/rad
-0.004 083
-0.004 903
-0.004 881
κ1/rad
0.108 648
0.098 837
0.099 504
κ2/rad
0.128 946
0.119 044
0.119 814
σ0/ 像素
0.341 602
0.321 956
0.303 820
参数
算法
LS解 Procrustes解 TLS解 WTLS解
ΔX/mm
3 389.731
3 389.785
3 389.731
3 389.726
ΔY/mm
188.563
188.691
188.563
188.546
ΔZ/mm
5 598.983
5 598.441
5 598.983
5 598.984
λ
0.999 661
0.999 664
0.999 664
0.999 638
φ/rad
-0.117 417
-0.117 941
-0.117 941
-0.118 118
ω/rad
0.041 652
0.040 140
0.040 140
0.040 092
κ/rad
0.010 433
0.015 252
0.015 252
0.015 311
σ0/mm
11.592 88
3.434 561
3.420 081
3.113 425
| [1] | Chen Yi, Lu Jue, Zheng Bo. Research on Close-Range Photogrammetry with Big Rotation Angle[J].Acta Geodaetica et Cartographica, 2008, 37(4):458-468(陈义,陆珏,郑波. 近景摄影测量中大角度问题的探讨[J]. 测绘学报,2008,37(4):458-468) |
| [2] | Kang Zhizhong, Zhang Zuxun, Yang FanLin.Relative Orientation and Epipolar Arrangement Based on Forward Moving Image Pairs Along the Optical Axis[J].Acta Geodaetica et Cartographica, 2007, 36(1):56-61(康志忠,张祖勋,阳凡林.基于沿主光轴方向摄影立体像对的相对定向与核线排列[J].测绘学报,2007,36(1):56-61) |
| [3] | Zhang Yongjun, Xiong Jinxin, Xiong Xiaodong, et al. Main Error Source of Vertical Parallax and Compensation Regression Model of POS Data[J]. Acta Geodaetica et Cartographica, 2011, 40(5):604-609(张永军,熊金鑫,熊晓东,等. POS数据的上下视差误差源检测及误差补偿回归模型[J].测绘学报,2011,40(5):604-609) |
| [4] | Fang X. Weighted Total Least Squares: Necessary and Sufficient Conditions, Fixed and Random Parameters[J]. Journal of Geodesy, 2013, 87(8):733-749 |
| [5] | Mahboub V, Sharifi M A. On Weighted Total Least-Squares with Linear and Quadratic Constraints[J]. Journal of Geodesy, 2013, 87(3):279-286 |
| [6] | Mahboub B. On Weighted Total Least-Squares for Geodetic Transformations[J]. Journal of Geodesy,2012,86(5):359-367 |
| [7] | Zhou Yongjun, Zhu Jianjun, Deng Caihua. The Consistency Between Row-Wised Weighted Total Least Squares and Condition Adjustment with Parameters[J]. Acta Geodaetica et Cartographica, 2012, 41(1):48-53(周拥军,朱建军,邓才华.附参数的条件平差与按行独立的加权总体最小二乘平差法估计的一致性研究[J]. 测绘学报,2012,41(1):48-53) |
| [8] | Wang Leyang, Xu Caijun. Total Least Squares Adjustment with Weight Scaling Factor[J].Geomatics and Information Science of Wuhan University, 2011, 36(8):887-890 (王乐洋,许才军.附有相对权比的总体最小二乘平差[J]. 武汉大学学报·信息科学版,2011,36(8):887-890) |
| [9] | Chen Yi, Lu Jue, Zheng Bo. Application of Total Least Squares to Space Resection[J]. Geomatics and Information Science of Wuhan University, 2008, 33(12):1 271-1 274(陈义,陆珏,郑波.总体最小二乘平差方法在空间后方交会中的应用[J].武汉大学学报·信息科学版,2008,33(12):1 271-1 274) |
| [10] | Wang Zhizhuo. Principle of Photogrammetry[M]. Wuhan: Wuhan Technical University Press, 1990(王之卓. 摄影测量原理[M]. 武汉:武汉大学出版社,1990) |
 2015, Vol. 40
2015, Vol. 40



