文章信息
- 刘帅, 朱亚杰, 薛磊
- LIU Shuai, ZHU Yajie, XUE Lei
- 一种结合稀疏表示和纹理分块的遥感影像超分辨率方法
- Remote Sensing Image Super-Resolution Method Using Sparse Representation and Classified Texture Patches
- 武汉大学学报·信息科学版, 2015, 40(5): 578-582
- Geomatics and Information Science of Wuhan University, 2015, 40(5): 578-582
- http://dx.doi.org/10.13203/j.whugis20130385
-
文章历史
- 收稿日期:2013-08-06
2. 北京大学遥感与地理信息系统研究所, 北京, 100871
2. Institute of Remote Sensing and Geographic Information System, Peking University, Beijing 100871, China
高分辨率遥感图像在国民经济建设、城市信息提取、精准农业,以及军事测绘等方面都有着广泛的应用前景[1,2]。遥感图像的空间分辨率是衡量卫星遥感性能的一项主要指标,获取高分辨率图像是我国卫星遥感领域迫切需要解决的关键问题之一。提高遥感图像的空间分辨率最直接的方法就是通过改良硬件来提高分辨率,但这种方法不仅难度大而且成本高,同时改善硬件也不能在短时间内完成。因此,利用超分辨率方法来提高遥感图像分辨率具有重要的现实意义。图像超分辨率是指从观测图像中估计不失真的高分辨率图像的技术,这是一个逆问题,也是非适定数学反问题求解的过程[3]。图像超分辨率的基本思想最初是由Harris于上世纪60年代在单幅图像复原的概念和方法的基础上逐步形成并发展起来的[4]。从80年代后期以来,随着计算机、电子、信号处理技术以及一些优化理论的发展,图像超分辨率问题取得了快速的发展。
就目前的研究成果和应用而言,传统的插值方法不能增加图像的有效信息,随着放大倍数的增加,图像视觉效果较差,且会出现锯齿效应。基于重建的方法研究很多,比较典型的有最大后验概率方法[5]、迭代反向投影法[6]和凸集投影法[7]。由于低分辨率图像不能提供足够的先验信息,在图像分辨率倍数增加的情况下,重建方法的效果也较差。为了提高图像清晰度,需要加入更多的先验知识,因此,基于学习的超分辨率方法应运而生。基于学习的方法首先选定一组高分辨率和低分辨率训练图像集,然后建立这两种训练图像集的对应关系,再由这种对应关系重建高分辨率图像。
稀疏表示理论是一种新颖的基于学习的方法,近年来引起了很多研究者的关注,并在图像处理领域发挥了重要的作用[8,9,10]。图像稀疏表示即在由冗余字典张成的整个信号空间依据稀疏度量标准寻找最优解。本文将稀疏表示理论应用于遥感影像处理,给出了一种结合分块稀疏表示和纹理结构的遥感图像超分辨率方法,并针对遥感影像进行了实验。
1 稀疏表示原理
设 x ∈Rn为图像的向量表示,D ∈Rn×k 表示过完备字典,k为字典中基原子数目,则 x 可由字典D基原子的线性组合表示:
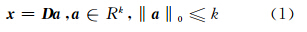
式中,a 是稀疏表示系数,为一仅含有少量非零值的向量;D = D 1 D 2 … D k ,D i∈Rn 。‖a ‖0≤k表示对a 的稀疏约束,用零范数计算向量a 中非零元素的个数。 这样,图像信号可以用一个字典中少量基原子的线性组合来表示。求解稀疏表示系数属于NP问题,大量的研究集中于利用一范优化来近似求解零范数问题,公式可以转化为[11,12]:
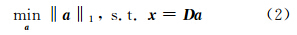
理论上已经证明 a足够稀疏时,上述问题的解是唯一的,且一范代替零范可以有相同的稀疏解。在具体应用建模时,还要考虑到观测图像可能被噪声污染,因此,考虑到噪声因素的图像稀疏表示转变为:
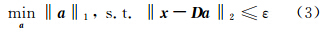
本文在遥感图像应用中引入正则化项,将式(3)转化为凸优化问题:

字典学习是超分辨重构的关键步骤。应用稀疏表示方法,选取训练的高低分辨率遥感图像进行分块,通过对高分辨率遥感图像块样本x = x 1 x 2 … x N 和低分辨率遥感图像块样本y = y 1 y 2 … y N 进行训练,建立二者之间的联系。使图像块 x i和 y i在高分辨率图像字典D x和低分辨率图像字典Dy上有相同的稀疏表示:
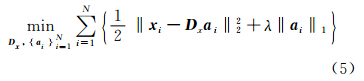
和
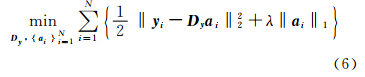
结合这些目标,对以上的公式联合训练,可以写成为:
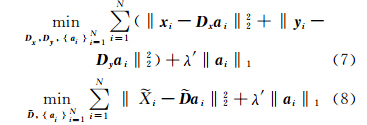
其中,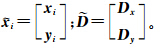
式(8)可以采用 K-SVD算法求解[13],通过k次奇异值分解(SVD)过程实现。
1) 设置随机正则化字典 。
2) 稀疏编码阶段,固定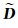 ,求解稀疏表示系数 a i,常用的算法有线性规划方法和贪心算法。 由于线性规划方法在解决规模较大问题时计算复杂度较高,本文采用正交匹配追踪(OMP)求解[14]。
,求解稀疏表示系数 a i,常用的算法有线性规划方法和贪心算法。 由于线性规划方法在解决规模较大问题时计算复杂度较高,本文采用正交匹配追踪(OMP)求解[14]。
3) 字典更新阶段。这一步稀疏表示系数已知,不考虑等号右边第二项,式(8)可以写为:

式中, ;k为字典中原子的个数;a Tk表示系数矩阵a的第k行。限制 Ek为使用原子dk的字典基元集合的列向量,进行SVD分解,E k= UΔ VT,用矩阵U的第一列更新原子dk,用矩阵V 的第一列乘以对角阵的值Δ 1,1更新a kT中的对应元素。
;k为字典中原子的个数;a Tk表示系数矩阵a的第k行。限制 Ek为使用原子dk的字典基元集合的列向量,进行SVD分解,E k= UΔ VT,用矩阵U的第一列更新原子dk,用矩阵V 的第一列乘以对角阵的值Δ 1,1更新a kT中的对应元素。
4) 返回第二步,进行迭代。
算法经过有限次迭代,可获得式(9)的解,从而训练出字典对。
2.2 结合稀疏表示和纹理分块的遥感图像超分辨率
首先根据纹理结构将遥感图像划分成平滑块和非平滑块两类,平滑块与非平滑块的判别采用计算标准差作为阈值,公式为:
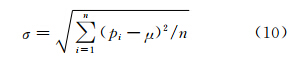
其中,pi为像素值;μ为图像块像素的均值;n为像素点总数。由于平滑块像素值比较平均,直接采用三次卷积的方法就能获得较好的效果,且计算复杂度比较低;对于非平滑块采用稀疏表示的方法重构,这种方法计算复杂度比较高。通过纹理结构的平滑与否来选择超分辨率算法,可以减少超分辨率运算的时间。
在实际的遥感观测中,设y ∈Rm为低分辨率图像块,x ∈Rn为理想的高分辨率图像块, S ∈Rm×n为下采样矩阵, H 为系统观测矩阵, n 为系统噪声,则遥感图像的观测模型可表示为:

忽略系统噪声,非平滑遥感图像块的超分辨率问题可描述为:

由式(1)可 得y的近似 = SHDa ,在 a 充分稀疏的条件下,高分辨率遥感图像块的稀疏表示可由其对应的低分辨率遥感图像块的稀疏表示来表达。由于将低分辨率图像块的细节作为特征重建效果较好,本文使用一阶和二阶梯度提取低分辨率图像块的特征[15]。
对每个低分辨率遥感图块 y i,参考式(4)可以考虑如下优化问题:

其中,Dy为低分辨率图像块的字典,由字典训练得到; a i为遥感图像块的稀疏表示系数; F 为特征提取滤波器。通过式(13),可以得到解 a i。由于低分辨率字典与高分辨率字典是一一对应的,则高分辨率图像 x 的第i个局部块 x i可由高分辨率图像块字典D x表示为 x i=D x a i, a i同时为高低分辨率遥感图像块的稀疏表示系数。如此对每个低分辨率遥感图像块进行处理,便得到高分辨率图像块 x 。
在对每个遥感图像块都处理完成后,组成高分辨率遥感初始图像 X 0= x i ki=k 。由于重构的图像可能不满足条件式(4),忽略系统噪声 n ,设置全局约束条件:

式中,S 是下采样矩阵; H 为系统观测矩阵;最后输出的是超分辨率重构图像 X 。
3 实验与结果分析
遥感图像的局部结构存在着共同的纹理、边界等细节信息,因此可以利用稀疏表示的方法通过字典学习建立高低分辨率图像块之间的联系,求出图像块稀疏表示系数,从而重构高分辨率遥感图像。首先以离线的方式进行字典学习,随机提取10 000块高分辨率遥感图像块,经过下采样后得到低分辨率遥感图像块,形成高、低分辨率遥感图像块对,放大因子取3,训练出的字典 D x和 D y 均包含1 024个原子。重构时选取输入图像为原始全色遥感影像中的植被区域和建筑区域的裁剪图像,将建筑和植被影像下采样成低分辨率图像,遥感图像块选取5×5的大小进行实验,块间最大重叠。根据遥感图像纹理统计信息,将图像块分成平滑块和非平滑块两大类。平滑块直接采用双三次卷积重构,非平滑块根据字典学习阶段求得的冗余字典以及稀疏表示系数。计算低分辨率图像块对应的高分辨率图像块,最后将所有的高分辨率图像块合成最终的高分辨率图像。为了验证遥感图像超分辨率的效果,本文采用的测试数据是WorldView-2卫星全色影像(见图 1),字典学习的图像也取自Worldview-2卫星高分辨率影像。本文算法运行软件环境为Matlab,硬件环境为CPU Intel i5 1.70 GHZ,内存4 GB。

|
| 图 1 实验图像 Fig. 1 Experimental Images |
本文对利用双线性插值(Bilinear)算法、双三次卷积(Bicubic)算法、Yang算法[12]和本文算法得到的遥感图像超分辨率效果进行了比较。实验分别从超分辨率遥感图像的视觉效果、均方根误差(root mean square error,RMSE)和峰值信噪比(peak signal to noise ratio,PSNR)三个方面来评价结果。实验中采用建筑和植被两影像进行测试,图 2和图 3分别是建筑影像与植被影像超分辨率效果,由图 2、3中可以看出,双线性插值算法和双三次卷积算法重构的图像细节模糊,存在过度平滑现象,Yang算法获得的图像比前两种算法清晰,但计算复杂度较高,平均计算时间较长。比较而言,本文算法有较好的整体视觉效果,且重构的速度比Yang算法要快,重构一幅图像平均时间约24.7 s。

|
| 图 2 4种算法对建筑影像超分辨重构效果 Fig. 2 Super-resolution Reconstruction Building Images Using Four Algorithms |

|
| 图 3 4种算法对植被影像超分辨率重构效果 Fig. 3 Super-resolution Reconstruction Vegetation Images Using Four Algorithms |
尽管通过视觉观察比较直接,但其易受人主观因素的影响。客观评价通常考察重构图像与理想图像之间的偏差程度,偏差越小,说明重构的效果越好。表 1给出了利用以上4种算法重构影像的RMSE和PSNR的比较。 从表 1中可以看出,本文算法重构建筑影像的RMSE值比其他算法小,说明本文算法超分辨率结果相对于原始高分辨率影像的偏差较小,而PSNR值则明显高于其他算法。对于植被影像,本文算法效果略低于Yang算法,但计算时间比Yang算法短。总体上,本文算法能较好地重构高分辨率影像的细节和纹理特征 。
| 算法 | 建筑影像 | 植被影像 | ||
| RMSE | PSNR | RMSE | PSNR | |
| Bilinear | 16.801 | 23.624 | 85.260 | 9.516 |
| Bicubic | 15.420 | 24.369 | 86.184 | 9.422 |
| Yang算法 | 13.687 | 25.405 | 88.099 | 9.231 |
| 本文算法 | 13.461 | 25.549 | 87.493 | 9.291 |
本文将稀疏表示理论应用于遥感图像超分辨率重构。通过训练获取高、低分辨率图像块的字典对,对需要重构的低分辨率遥感图像分块,根据纹理结构划分为平滑块和非平滑块。对非平滑块,通过学习获取遥感图像块的稀疏表示系数,并与高分辨率字典结合重构出高分辨率遥感图像块,对平滑块直接采用双三次卷积的方法重构。实验结果说明稀疏表示方法在视觉效果、均方误差和峰值信噪比三个方面都优于传统插值方法。稀疏表示方法有较好的遥感影像超分辨率效果,能较好地重构高分辨率影像的细节和纹理信息,为后续的遥感图像处理和信息提取奠定了良好的基础。
| [1] | Huang X, Zhang L. An SVM Ensemble Approach Combining Spectral, Structural, and Semantic Features for the Classification of High-Resolution Remotely Sensed Imagery [J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(1): 257-272 |
| [2] | Zhang Qian, Huang Xin, Zhang Liangpei. Multiscale Image Segmentation and Classification with Supervised ECHO of High Spatial Resolution Remotely Sensed Imagery [J]. Geomatics and Information Science of Wuhan University, 2011, 36(1):117-121 (张倩, 黄昕, 张良培. 多尺度同质区域提取的高分辨率遥感影像分类研究 [J]. 武汉大学学报·信息科学版, 2011, 36(1): 117-121) |
| [3] | Dong W, Zhang L, Shi G, et al. Image Deblurring and Super-resolution by Adaptive Sparse Domain Selection and Adaptive Regularization [J]. IEEE Transactions on Image Processing, 2011, 20(7): 1 838-1 857 |
| [4] | Harris J. Diffraction and Resolving Power[J]. Journal of the Optical Society of America, 1964, 54(7): 931-936 |
| [5] | Shen Huanfeng, Li Pingxiang, Zhang Liangpei. Adaptive Regularized MAP Super-Resolution Reconstruction Method[J]. Geomatics and Information Science of Wuhan University, 2006, 31(11): 949-952 (沈焕锋, 李平湘, 张良培. 一种自适应正则MAP超分辨率重建方法 [J]. 武汉大学学报·信息科学版, 2006, 31(11): 949-952) |
| [6] | Irani M, Peleg S. Improving Resolution by Image Registration [J]. CVGIP: Graphical models and Image Processing, 1991, 53(3): 231-239 |
| [7] | Stark H, Oskoui P. High-Resolution Image Recovery from Image-Plane Arrays, Using Convex Projections [J]. Journal of the Optical Society of America A, 1989, 6(11): 1 715-1 726 |
| [8] | Lan Chengdong, Chen Liang, Lu Tao. Face Super-resolution Using Sparse Representation with Position Weights[J]. Geomatics and Information Science of Wuhan University, 2013, 38(1): 27-30 (兰诚栋, 陈亮, 卢涛. 利用位置权重稀疏表示的人脸超分辨率算法 [J]. 武汉大学学报·信息科学版, 2013, 38(1): 27-30) |
| [9] | Song Xiangfa, Jiao Licheng. Classification of Hyperspectral Remote Sensing Image Based on Sparse Representation and Spectral Information[J]. Journal of Electronics & Information Technology, 2012, 34(2): 268-272 (宋相法, 焦李成. 基于稀疏表示及光谱信息的高光谱遥感图像分类 [J]. 电子与信息学报, 2012, 34(2): 268-272) |
| [10] | Lian Qiusheng, Zhou Ting. Adaptive Compressed Imaging Algorithm Combined the Sparse Representation in the Dictionaries with Non-Local Similarity[J]. Acta Electronica Sinica, 2012, 40(7): 1 416-1 422(练秋生, 周婷. 结合字典稀疏表示和非局部相似性的自适应压缩成像算法 [J]. 电子学报, 2012, 40(7): 1 416-1 422) |
| [11] | Tropp J A. Just Relax: Convex Programming Methods for Identifying Sparse Signals in Noise [J]. IEEE Transactions on Information Theory, 2006, 52(3): 1 030-1 051 |
| [12] | Yang J, Wright J, Huang T, et al. Image Super-Resolution as Sparse Representation of Raw Image Patches [C]. IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, 2008 |
| [13] | Aharon M, Elad M, Bruckstein A. K-SVD: An Algorithm for Designing Overcomplete Dictionaries for Sparse Representation [J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4 311-4 322 |
| [14] | Needell D, Vershynin R. Signal Recovery From Incomplete and Inaccurate Measurements Via Regularized Orthogonal Matching Pursuit [J]. IEEE Journal of Selected Topics in Signal Processing, 2010, 4(2): 310-316 |
| [15] | Hong C, Dit-Yan Y, Yimin X. Super-Resolution through Neighbor Embedding [C]. IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Washington D C, USA, 2004 |
 2015, Vol. 40
2015, Vol. 40


