文章信息
- 郑肇葆, 潘励, 郑宏
- ZHENG Zhaobao, PAN Li, ZHENG Hong
- 应用图像关联度的图像模糊分类
- Application of Image Correlation Degree to Image Fuzzy Classification
- 武汉大学学报·信息科学版, 2015, 40(5): 574-577
- Geomatics and Information Science of Wuhan University, 2015, 40(5): 574-577
- http://dx.doi.org/10.13203/j.whugis20140736
-
文章历史
- 收稿日期:2014-10-08
2. 武汉大学电子信息学院, 湖北 武汉, 430072
2. Electronic Information School, Wuhan University, Wuhan 430072, China
图像纹理分类是图像自动解译的关键技术,早在二十多年前,文献[1]利用“Tuned” 纹理模板与原始图像作卷积,求得能反映纹理特征的纹理能量,进行图像的纹理分类。图像纹理分类的质量取决于最优“Tuned”纹理模板的获得。之后,如何获得最优“Tuned”模板的研究引起从事图像自动解译科研人员的注意,先后出现了产生纹理“Tuned”模板的遗传算法[2]、产生“Tuned”模板的Bayesian Networks方法[3]、产生最佳“Tuned”模板的蜜蜂交配算法[4]等。随着确定最佳“Tuned”模板方法的改进,纹理图像分类的质量得到提高。但是一个最佳“Tuned”模板只适用于特定的一组图像,假定是居民地图像,则山地、水田这组图像的分类计算量较大。最近十余年出现了基于模糊规则和模糊推理的图像分类方法[5\|6]。这一类图像模糊分类是建立在知识库、规则库的基础上的,而知识库和规则库的建立不是一件容易的事。本文提出的图像模糊分类方法无须建立知识库和规则库,而是借助模糊计算中关联度的概念来实现图像的模糊分类。
1 应用图像关联度的图像模糊分类 1.1 基本思想
首先,对待分类图像计算出每幅图像的灰度或其他纹理特征的均值;然后,根据特征均值的大小将图像分成几类,假定分成3类(即有3类不同属性的图像),每类图像数量假定为n1、n2、n3。计算每类图像的特征均值,接着计算每幅图像相对3个类别的关联度,所谓关联度,它反映一幅图像与所在类别和其他两个类别关系密切的程度。在这个基础上,分别计算每个类别中所有图像关联度的均值和标准差σ,计算每幅图像的关联度与该类图像关联度均值之差Δi。若Δi>2σ,则该图像“离开”该类别;否则,“保留”在该类别中。“离开”图像应进入哪一类别由该图像相对另两类的关联度决定,哪一类的关联度大就进入那一类。每幅图像都要经过“保留”与“离开”的检查,这样的检查意味着图像再分类。
1.2 图像与图像类别的关联度
假定有3组图像1、2、3组成一个组合,每组图像的像幅数分别为n1、n2、n3,每组图像纹理特征均值分别为mean1、mean2、mean3。
计算每幅图像纹理特征相对3组图像纹理特征均值之差,即第一组图像特征相对第一、二、三组特征均值的差为 d1(i1,1)、d1(i1,2)、d1(i1,3):

式中,Rbs(i1,1)表示第一组图像中第i1幅图像的纹理特征;d1(i1,1)、d1(i1,2)、d1(i1,3)分别表示第一组图像中第i1幅图像特征与第一组图像特征均值之差的绝对值、与第二组图像特征均值之差的绝对值、与第三组图像特征均值之差的绝对值。
类似地,有:
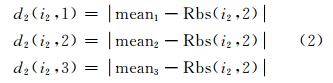
式中,Rbs(i2,2)表示第二组中第i2幅图像的纹理特征;d2(i2,1)、d2(i2,2)、d2(i2,3)分别表示第二组图像中第i2幅图像特征与第一组图像特征均值、第二组图像特征均值、第三组图像特征均值之差的绝对值。

式中符号与式(1)、式(2)中相应的符号有类似的意义。
接着可以计算每幅图像相对三组图像的每一组的关联度。第一组中每幅图像相对三个组的关联度为R1(i1,1)、R1(i1,2)、R1(i1,3):
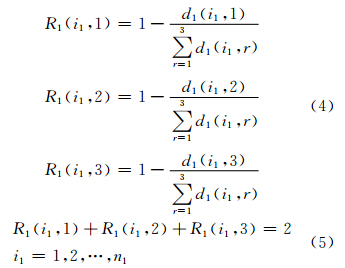
式中,R1(i1,1)表示第一组中第i1幅图像相对第一组的关联度;类似地,R1(i1,2)、R1(i1,3)表示第一组中第i1幅图像相对第二、三组的关联度。式(4)中右方第二项的分母表示第i1幅图像特征与3个组图像特征均值之差的代数和。式(5)表示关联度一个特征,即一幅图像相对3组图像的3个关联度之和等于2。
类似式(4),可以求得第二组、第三组中每幅图像相对三个组的关联度为R2(i2,1)、R2(i2,2)、R2(i2,3)和R3(i3,1)、R3(i3,2)、R3(i3,3)。
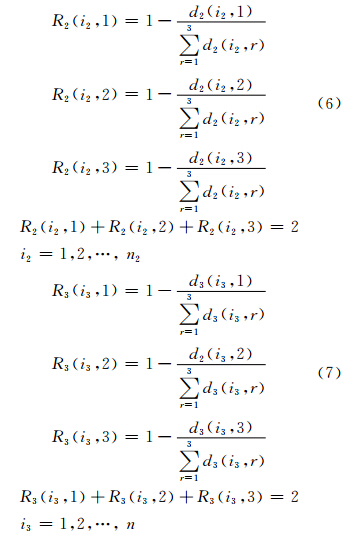
1) 对每幅待分类的图像,计算它的分形维特征[7]和能量特征[2]。
2) 按特征(分形维)的大小,将图像分成3类,假定待分类图像有3类。
3) 假定3类图像的像幅数分别为 n1、n2、n3,计算每一类图像特征的特征均值,它们分别为mean1、mean2、mean3。
4) 按式(1)、(2)、(3),分别计算每幅图像与一、二、三类图像特征均值的差d1(i1,1)、d1(i1,2)、d1(i1,3),d2(i2,1)、d2(i2,2)、d2(i2,3),d3(i3,1)、d3(i3,2)、d3(i3,3)。
5) 按式(4)~(7)分别计算每幅图像与一、二、三类图像的关联度R1(i1,1)、R1(i1,2)、R1(i1,3),R2(i2,1)、R2(i2,2)、R2(i2,3)和R3(i3,1)、R3(i3,2)、R3(i3,3)。
6) 计算3类图像在各自类别中关联度的均值f1、f2、f3和相应的标准差σ1、σ2、σ3。即从R1(i1,1)(i1=1,2,…,n1)中计算均值f1、标准差σ1。从R2(i2,2)(i2=1,2,…,n2)和R3(i3,3)(i3=1,2,…,n3)中计算相应均值f2、f3和相应标准差σ2、σ3。
7) 确定每幅图像是否归属于当前所在的类别。分别计算每个类别中每幅图像的关联度与该类图像关联度均值之差:
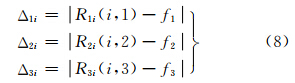
式中,R1i(i,1)、R2i(i,2)、R3i(i,3)分别表示第一、二、三类中每幅图像的关联度; f1、f2、f3分别表示第一、二、三类中图像关联度均值;Δ1i、Δ2i、Δ3i分别表示三类图像中每幅图像在所在类别中关联度与所在类别图像关联度均值之差。
如果Δ1i>2σ1,则第一类中第i幅图像“离开”第一类;类似地,如果Δ2i>2σ2、Δ3i>2σ3,则第二、三类中相应图像应该离开所在类别。相反地,如果Δ1i≤2σ1、Δ2i≤2σ2、Δ3i≤2σ3,相应图像都应“保留”在所在类别中。
8) 离开所在类别的图像应进入哪个类别应看该图像相对另两类的关联度,关联度值大的,就划入相应类别。
以上计算对所有待分类的图像都执行一次,分类过程完成一次迭代,这时3个类别中图像与开始的图像划分相比不一样。在新划分的情况下,进入第二次迭代,重复步骤3~8的过程,直至不再产生“离开”情况为止,计算结束。
从上述计算过程可以看出,图像的“保留”与“离开”,离开后图像的“再归类”,都与图像的关联度密切相关。关联度的计算属于模糊计算的范畴。另一点应注意的是,图像是否保留在相应类别中决定相应的“2σi”,σi在每次迭代中是变化的,不是常量,是模糊的,所以本文提出图像分类是模糊分类。
2 实验与分析 为了验证本文提出的图像分类方法的可行性,采用航空影像(18 cm×18 cm)进行分类实验。实验图像中,灌木52幅,居民地23幅,河流35幅,水田13幅,山地21幅,共5类不同地物。实验将5类不同的地物图像分为3个不同的组合,它们是灌木、居民地、河流组合,灌木、山地、水田组合和山地、河流、水田组合。从实验中可以得到以下结论。
1) 不同图像组合方式,图像分类效果不同。从表 1中3个不同组合分类的情况可以看出,灌木图像在第1、2组合中正确识别率分别为44/52和52/52;河流图像在第1、3组合中正确识别率分别为26/35和35/35;山地图像在第2、3组合中正确识别率分别为20/21和21/21;水田图像在2、3组合中正确识别率为13/13和11/13。应将图像特征均值差异大的图像放在一个组合中,容易得到较好的分类效果。
| 灌木 居民地 河流 | 灌木 山地 水田 | 山地 水田 河流 | |
| 正确识别率 | 44/52 22/23 26/35 | 52/52 20/21 13/13 | 21/21 11/13 35/35 |
2) 采用不同的图像特征(分形维,图像能量),图像分类效果不同。比较表 1与表 2的分类结果可以看出,采用分形维特征的图像分类效果优于采用能量特征的分类结果。本文用来计算图像能量特征的模板不是最优“Tuned”模板,而是随机的。
| 灌木 居民地 河流 | 灌木 山地 水田 | 山地 水田 河流 | |
| 正确识别率 | 47/5 2 21/23 21/35 | 40/52 21/21 13/13 | 21/21 13/13 28/35 |
3) 采用本文提出的方法进行图像分类的结果如表 3所示。
| 灌木 | 河流 | 山地 | 水田 | 居民地 | |
| 准确率 | 52/52=1.0 | 35/35=1.0 | 21/21=1.0 | 13/13=1.0 | 22/23=0.96 |
4) 与几种优化“Tuned”模板的图像分类结果相比,本文提出的关联度图像分类结果有一定的优势。
由表 4中对比结果可见,本文提出的图像模糊分类方法是可行、有效的。在多种不同地物图像分类时,如何快速得到最佳地物图像搭配组合,有待进一步研究。
| [1] | You J, Cohen H A. Classification and Segmentation of Rotated and Scaled Textured Images Using Texture "Tuned" Mask[J]. Pattern Recognition, 1993, 26(2): 245-258 |
| [2] | Zheng Zhaobao, Zheng Hong. Genetic Algorithm for Producing Texture "Tuned" Masks[J]. PR & AI, 2001, 14(1):119-122(郑肇葆,郑宏. 产生纹理"Tuned"模板的遗传算法[J]. 模式识别与人工智能,2001, 14(1):119-122) |
| [3] | Zheng Zhaobao, Pan Li, Yu Xin. Bayesian Networks for Producing Texture "Tuned" Masks[J]. Geomatics and Information Science of Wuhan University, 2006, 31(4): 304-307(郑肇葆,潘励,虞欣. 产生 "Tuned"模板的Bayesian Networks 方法[J].武汉大学学报·信息科学版,2006, 31(4):304-307) |
| [4] | Zheng Zhaobao. Honey-Bee Mating Optimization Algorithm for Producing Better "Tuned" Masks[J]. Geomatics and Information Science of Wuhan University, 2009,34(4):387-390 (郑肇葆.产生最佳"Tuned"模板的蜜蜂交配算法[J].武汉大学学报·信息科学版,2009,34(4):387-390) |
| [5] | Cordón O. A Proposal on Reasoning Method in Fuzzy Rule-Based Classification System[J]. International Journal of Approximate Reasoning, 2009, 20: 21-45 |
| [6] | Sanz J A. IVTURS: A Linguistic Fuzzy Rule-Based Classification System Based on a New Interval-Valued Fuzzy Reasoning Method With Tuning and Rule Selection[J]. IEEE Transactions on Fuzzy Systems, 2013, 21 (3): 399-411 |
| [7] | Zheng Zhaobao, Huang Guilan. Using Least Square Method for Texture Classification of Aerial Image and Analysing Some Relative Problems[J]. Acta Geodaetica tt Cartographica Sinica,1996,25(2):21-26 (郑肇葆,黄桂兰. 航空影像纹理分类的最小二乘法和问题分析[J].测绘学报,1996,25(2):21-26) |
 2015, Vol. 40
2015, Vol. 40


