文章信息
- 杨晟炜, 刘真, 吴明光, 张桢杰
- YANG Shengwei, LIU Zhen, WU Mingguang, ZHANG Zhenjie
- 一种基于特征光谱匹配的多色分色方法
- Color Separation Method Based on Characteristic Spectrum Matching for Multi-color Reproduction
- 武汉大学学报·信息科学版, 2015, 40(4): 563-568
- Geomatics and Information Science of Wuhan University, 2015, 40(4): 563-568
- http://dx.doi.org/10.13203/j.whugis20130345
-
文章历史
- 收稿日期:2013-07-23
2. 上海理工大学出版印刷与艺术设计学院, 上海, 20009;
3. 南京师范大学虚拟地理环境教育部重点实验室, 江苏 南京, 210046
2. College of Communication and Art Design, University of Shanghai for Science & Technology, Shanghai 200093, China;
3. Key Laboratory of Virtual Geographic Environment of Ministry of Education, Nanjing Normal University, Nanjing 210046, China
自然界物体的光谱反射曲线具有唯一性,通过光谱匹配复制得到的印刷品,在任何光源和观察条件下,都可以保持与原稿一致准确的颜色效果。多色印刷增加了可复制的光谱组合,扩大了色域,因此,基于光谱的多色复制技术已经成为了当前研究的热点。但多色复制会使颜色在光谱表征和油墨配比的转换模型变得复杂。当前研究普遍采用子空间划分的方法处理多基色复制问题,色差精度不高且效率较低。文献[1]提出,在所测得色彩的分光光谱数据中,对色彩特征表达最关键的光谱为特征光谱。因此,将特征光谱应用于分色过程可以有效提高色彩复制的效率。
在特征光谱研究方面,文献[2]提及,色彩特征波段数目越多,色彩空间表达或描述的精度越高。文献[3]指出,在实际应用中,光谱的低阶导数处理更有效。文献[4]提出了利用主成分分析法(PCA)提取光谱特征的方法和基色估计算法。在光谱分色方面,文献[5, 6]提出了改进的胞元搜索算法,并将色域划分为若干个三色与四色的子空间再进行分色转换。文献[7]研究了多色复制中光谱冗余的问题。文献[8, 9, 10]提出了根据色度角进行子空间判断的方法。以上研究没有将特征光谱的研究与多色分色算法相结合,分色算法都是基于全波段进行的;其次,在多色分色的过程中采用遍历子空间求解的方法,计算量很大。
针对以上问题,本文在利用光谱导数法对多色印刷的特征光谱进行提取的基础上,提出了基于特征光谱阈值范围的匹配方法,将其应用于多色印刷的分色过程;并提出了基于特征光谱和子空间判断的多色分色算法,有效地提高了色彩转换的精度和效率。 1 特征光谱提取和匹配
图 1中两条复制光谱与目标光谱的RRMS均为0.003 4,但复制光谱1的色差为3.83,复制光谱2的色差为0.11。从图 1中可以看出,在420~460 nm之间,复制光谱2与目标光谱更接近。因此,分析光谱中对于颜色复制更加重要的波段对提高光谱分色精度有着重要的意义。
 |
| 图 1 目标光谱与复制光谱对比图Fig. 1 Spectrum Comparison Diagram Between Desired and Reproduction Spectrum |
光谱导数变换是指对目标反射或透射光谱的数学模拟和不同阶数导数的计算,通过计算,能快速确定光谱转折点以及最大、最小反射或透射率的波长位置。光谱导数变换能够提取不同的特征光谱参数,如波长位置、峰值等,还能够根据需要来分解或叠合相关波段,进一步提取各种目标参数[1]。一般情况下离散光谱的导数如式(1)所示:
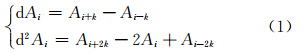
式中,Ai为第i个波段的光谱反射率;k为波长索引的间隔,通常为1。
测量每种彩色基色的单色梯尺获得原始光谱反射率,再对其进行一阶和二阶导数变换,提取以下两类波段为特征波段: ① 一阶导数产生明显的波峰和波谷的波段,这些波段原始光谱反射率变化最快; ② 一阶导数约等于0的波段,通过对应波段二阶导数的正负情况,可以判断这些波段原始光谱反射率是否达到了极大值或极小值。 1.2 特征光谱匹配
光谱匹配的前提是利用一种有效便捷的方法来表示光谱曲线,本文采用多阈值的光谱曲线编码方式。由于一阶和二阶导数曲线值有正有负,因此阈值划分是将整个值域在正值域和负值域内分别平均划分为N个分区,阈值为各分区的间隔点,将光谱反射率按照阈值范围进行编码:
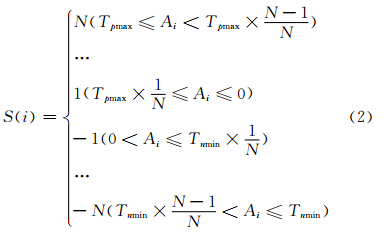
式中,S(i)是第i个特征光谱波段的编码;Ai是该波段的光谱反射率;T为阈值;Tpmax为正值域的最大值;Tnmin是负值域的最小值;N为分区数。整个光谱值域共分为2N个区间。
由于不同的网点面积率的基色叠加形成的色块在各个波段反射的光谱程度不同,其一阶导数和二阶导数的值域也不同,因此我们可以提取各子空间内所有色块的一阶导数和二阶导数经过编码后的编码范围,表示该子空间所能复制的颜色特征。曲线编码范围的提取算法如式(3):
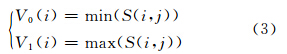
式中,V0(i)表示所有色块第i个特征光谱波段编码的最小值;V1(i)表示所有色块第i个特征光谱波段编码的最大值;S(i,j)是第j个色块第i个特征光谱波段的编码。
特征光谱匹配时,比较样本颜色导数光谱曲线与特征光谱编码范围的相似性,相似性的衡量尺度类似于二进制编码间的Hamming距离,如式(4)~(5)所示:

式中,D(i)、A(i)分别表示样本曲线第i个特征光谱波段的距离和编码,编码在特征光谱编码范围内时距离为0,在范围外则距离为1;n为特征波段的数量。由于不同颜色的特征波段数量不同,所以光谱的距离D为各波段距离之和与特征波段数量的比值,距离越大表示两个曲线间的光谱形状差异越大。 2 基于特征光谱匹配的分色算法
现有研究通常将色彩空间划分为若干个三色或四色子空间来解决多基色色彩转换模型复杂的问题,位于每个空间内的颜色由构成该空间的基色进行复制。以本文采用的HPZ3200 CMYKRGB七色喷墨打印机为例,为了尽可能多地表现可复制的光谱范围,根据各基色在Lab空间中的位置,将打印机可复制的色域分为CGYK、YRMK、MBCK、CMYK、RGBK 5个四色子空间和BCG、GYR、RMB 3个三色子空间。在进行分色时,针对目标色样点,基于色度方式的色彩转换模型,根据颜色的色相角判断目标颜色所在的子空间[8, 9, 10]。但基于光谱的色彩转换模型在子空间判断上相对复杂,现有研究均采用遍历子空间求解的方式,计算量很大,约为经过子空间判断的N倍(N为子空间的数量),转换效率极低。因此,使用从特征光谱匹配的角度寻找子空间判断的方法以及将特征光谱用于分色的算法,能够显著提高光谱色彩转换的精度和效率。 2.1 子空间特征光谱编码范围提取
通过前期研究可以发现,不仅不同子空间的特征光谱编码范围差异较大,同一个子空间内的特征光谱编码范围变化也比较大,如图 2所示。
 |
| 图 2 CGYK子空间色块光谱一阶导数曲线 Fig. 2 First Derivative Spectrum of CGYK Sub Space |
图 2是CGYK子空间不同面积率叠加色块的一阶导数,图 2(a)中色块满足黄基色网点面积率大于青基色网点面积率大于绿基色网点面积率的条件,图 2(b)中色块满足黄基色网点面积率小于青基色网点面积率小于绿基色网点面积率的条件,所有色块的黑基色网点面积率为0。将整个值域按照式(2)所述划分为6个区间,可以看出,当网点面积率的比例不同时,一阶导数的值域范围变化较大。例如在500 nm处,图 2(a)的值域范围为1~3,图 2(b)中则为1~2;在650 nm处,图 2(a)的值域为正,而图 2(b)的值域为负。
因此,为了提高子空间特征光谱编码范围提取的准确性,在每个子空间打印不同网点面积率叠印的色块,并按照三个彩色基色网点面积率的比例划分,分别依式(2)、式(3)提取一阶和二阶导数的编码范围,即每个子空间提取6组特征光谱编码范围。 2.2 光谱分色算法
光谱分色采用胞元N值修正的光谱纽介堡方程(CYNSN)[11, 12],算法流程如图 3所示。
 |
| 图 3 光谱分色算法流程图Fig. 3 Algorithm Flow of Spectral Color Separation |
首先将目标光谱反射率进行子空间判断,找出符合条件的K个候选子空间,在每个候选子空间中分别基于全波段和特征波利用反向CYNSN模型求解油墨配比,再利用正向CYNSN模型预测这2K组油墨配比的理论光谱反射率,计算其与目标光谱反射率之间的RRMS和色差ΔE,若存在油墨配比满足RRMS小于0.01,ΔE小于1.5,则选择符合条件的油墨配比中RRMS最小的一组为最优解,若不满足这个条件,则增大子空间判断的容差,重复进行子空间判断和求解的过程,直到K为最大值,即遍历所有子空间为止。
子空间的判断过程和准则如下。
1) 根据式(2)将目标光谱反射率进行编码;
2) 根据式(4)分别计算目标光谱编码与各个子空间特征光谱编码范围的距离。其中各子空间的特征光谱编码范围按照§2.1提取,子空间的距离为一阶导数曲线的距离与二阶导数曲线的距离之和;
3) 将目标光谱与各子空间的距离升序排列。其中每个子空间取6组配比的最小距离作为目标光谱与该子空间的距离;
4) 假设最小距离为Dmin,由于目标光谱与各子空间之间的距离可能相同或相近,因此选择距离在[Dmin,Dmin+2]之间的子空间为候选子空间;
5) 按照本文所述进行反解和最优解判断,若无法获得最优解,则扩大步骤4)的距离候选范围,直到遍历所有子空间为止。 3 实验结果与分析
实验采用HPZ3200 CMYKRGB七色喷墨打印机,分为CGYK、YRMK、MBCK、CMYK、RGBK共5个四色子空间和BCG、GYR、RMB共3个三色子空间,每个子空间训练样本由各基色以0、20、40、60、80、100为油墨覆盖率排列组合而成,即四色子空间1 296个,三色子空间216个;测试样本由各基色以0、25、50、75、100排列组合而成,即四色子空间625个,三色子空间125个。 3.1 特征光谱分色精度分析
在每个子空间内,分别基于全波段和特征波段求解测试样本对应的油墨配比,按照求解的结果重新打印测试样本,测量并计算测试样本与求解样本的RRMS和色差,实验结果如表 1所示。
| 子空间 | RRMS | ΔE*ab(D50,2°) | ||||||
| 特征波段 | 全波段 | 特征波段 | 全波段 | |||||
| Mean | Max | Mean | Max | Mean | Max | Mean | Max | |
| CGYK | 0.004 3 | 0.034 4 | 0.004 4 | 0.026 6 | 1.42 | 5.12 | 1.51 | 8.83 |
| YRMK | 0.005 5 | 0.061 1 | 0.004 4 | 0.022 3 | 2.13 | 8.60 | 2.12 | 27.19 |
| MBCK | 0.004 6 | 0.020 9 | 0.004 4 | 0.023 3 | 1.73 | 7.82 | 1.77 | 14.17 |
| CMYK | 0.004 1 | 0.027 1 | 0.003 8 | 0.026 9 | 1.37 | 4.67 | 1.26 | 10.10 |
| RGBK | 0.003 8 | 0.027 8 | 0.003 4 | 0.024 3 | 0.79 | 3.74 | 0.81 | 5.26 |
| BCG | 0.002 9 | 0.015 0 | 0.002 7 | 0.013 8 | 0.71 | 4.66 | 0.72 | 6.78 |
| GYR | 0.003 0 | 0.015 3 | 0.003 4 | 0.023 2 | 1.21 | 4.95 | 1.14 | 9.65 |
| RMB | 0.004 0 | 0.018 3 | 0.003 5 | 0.012 9 | 1.02 | 4.72 | 1.03 | 8.89 |
从表 1可以看出,总体来说,基于特征光谱求解油墨配比的RRMS精度略低于基于全波段求解的RRMS精度,但都达到了较高的精度。而在色差精度方面,不同子空间基于特征光谱与全波段求解的平均色差各有优势,但基于特征光谱求解的最大色差远小于基于全波段求解的色差。通过分析得出两个结论: ①基于特征波段的分色在保证RRMS精度的前提下,能够有效提高色差精度,尤其是最大色差;②无论RRMS还是色差都是基于全波段计算的,因此部分颜色基于全波段分色的精度高于特征波段求解。由此可知,将基于特征波段分色与基于全波段分色相结合可以得到更好的结果。 3.2 多色分色精度与效率分析
针对每个子空间,将该子空间的测试样本和其余子空间的测试样本分别与该子空间的特征光谱编码范围依式(4)、(5)进行相似性匹配判断。由于每个子空间的特征光谱波段数不同,故按照光谱距离占最远距离的百分比进行数据统计,结果见表 2。
| 子空间 | 相同子空间样本 | 其余子空间样本 | ||
| Dmean | Dmax | Dmean | Dmax | |
| CGYK | 2.70 | 10 | 13.50 | 43.33 |
| YRMK | 3.11 | 15.38 | 8.15 | 38.46 |
| MBCK | 6.27 | 22.35 | 24.63 | 52.94 |
| CMYK | 4.39 | 13.33 | 11.41 | 33.33 |
| RGBK | 4.26 | 15.79 | 7.46 | 34.21 |
| BCG | 2.05 | 15.63 | 18.89 | 53.13 |
| GYR | 2.86 | 37.50 | 17.40 | 53.13 |
| RMB | 4.72 | 20.59 | 20.93 | 67.65 |
从表 2可以看出,相同子空间的测试色块与该子空间特征光谱编码范围的平均距离约为2%~6.5%,而不同子空间的测试色块平均距离约为7.5%~24%,是相同子空间的3倍以上,而最大距离约为34%~67%,同样是相同子空间的 3倍以上。这说明利用特征光谱的距离进行子空间的判断是可行的。需要强调的是,其余子空间的测试样本中去除了625个与本子空间重叠的色块,若包含这些色块,则第三列的平均距离会减小。
在每个子空间内随机生成100个色块,共800个色块作为测试样本二。将测试样本二的光谱反射率分别按照三个流程求解油墨配比,流程一为§2.2所述流程,流程二按照文献[6]中的算法,遍历所有子空间分别求解墨水配比,并通过预测算法预测其与测试样本的RRMS,选择预测RRMS最小值对应的子空间和墨水配比作为结果。其中流程二基于全波段求解,流程一在反向CYNSN求解的过程中,采用郭晋一提出的胞元搜索算法[6]。流程三按照严爱国提出的基于色度的子空间判断方法判断色块所在子空间[8]的方法,在目标子空间内按照基于色度的方法求解墨水配比。光源选择D50,观察者选择2°视场。按照求解的结果重新打印测试样本,测量其光谱反射率,计算测试样本与求解样本的RRMS和色差,以及每个色块的求解次数,实验结果如表 3所示。
| 流程 | 求解次数 | RRMS | ΔE*ab(D50,2°) | ||
| Mean | Max | Mean | Max | ||
| 流程一 | 52.1 | 0.003 4 | 0.029 0 | 0.98 | 4.29 |
| 流程二 | 112 | 0.003 3 | 0.023 3 | 1.37 | 7.61 |
| 流程三 | 30.6 | 0.013 6 | 0.289 7 | 0.86 | 4.18 |
表 3的数据表明,本文提出的基于特征波段和全波段相结合的分色方法,平均RRMS为0.003 4,最大RRMS为0.029 0,略大于流程二,而平均色差0.98,最大色差4.29均优于流程二的结果。从运算量的角度考虑,使用本文采用的郭晋一的胞元搜索算法[6],每个四色或三色子空间需要选择最优的17个或9个胞元进行油墨配比的反解,所以对于每一个色块,流程二需要进行112次运算。本文提出的算法在每一个子空间分别基于特征波段和全波段进行分色,若按照遍历子空间的方式,则需要224次运算,但通过优化采用基于特征光谱匹配的子空间判断方法之后,平均仅需要52.1次运算,约为流程二的46%,在保证了分色精度的前提下,显著提高了分色的效率。与基于色度的流程三相比,流程一平均色度大于流程三的0.86,但平均RRMS远小于流程三的0.013 6,这符合基于光谱的色彩转换和基于色度的色彩转换的原理。同时,由于在一个子空间内进行了两次反解,计算量略大于流程三的30.6次。考虑到这只是在光源D50,2°视场下的结果,当光源和观察者改变时,结果也会发生变化。因此可认为,基于色度的子空间判断方法不适用于基于光谱的色彩转换。 4 结 语
本文在分析特征光谱的提取和匹配的基础上,分析了在光谱分色流程中进行子空间判断的流程和判断准则,同时将基于特征波段和全波段的分色方法进行了结合,提出了改进的分色算法流程。实验结果表明,提取的特征光谱编码范围能够显著代表各个子空间的光谱特征,特征波段和全波段相结合的分色方法在保证了RRMS精度的基础上,大大提高了色差的精度。而子空间判断算法显著降低了分色的运算次数,避免了遍历子空间造成的极大的计算量,具有较高的实用性。
| [1] | Wang Qiang. The Study on Color Management Mechanism of Spatial Information[D]. Wuhan:Wuhan University, 2005(王强. 空间信息的色彩管理机制研究[D]. 武汉:武汉大学, 2005) |
| [2] | Li A, Lennie P. Mechanisms Underlying Segmentation of Colored Textures[J]. Vision Research, 1997, 37(1):83-97 |
| [3] | Cloutis E A. Review Article Hyperspectral Geological Remote Sensing:Evaluation of Analytical Techniques[J]. International Journal of Remote Sensing, 1996, 17(12):2 215-2 242 |
| [4] | Tzeng D Y, Berns R S. A Review of Principal Component Analysis and Its Applications to Color Technology[J]. Color Research & Application, 2005, 30(2):84-98 |
| [5] | Wang Binyu, Xu Haisong, Luo M R. Color Separation Criteria for Spectral Multi-ink Printer Characterization[J]. Chin. Opt. Lett., 2012, 1:13 301-13 304 |
| [6] | Guo Jinyi, Xu Haisong, Luo M R. Novel Spectral Characterization Method for Color Printer Based on the Cellular Neugebauer Model[J]. Chin. Opt. Lett., 2010, 11:1 106-1 109 |
| [7] | Rosen M, Hattenberger E, Ohta N. Spectral Redundancy in a 6-ink Inkjet Printer[J]. Proc. of PICS, 2003:236-243 |
| [8] | Zhu Ming, Liu Zhen, Chen Guangxue.Research on Six-color Separation Model Based on Subarea Neugebauer Equations[J]. Acta Optica Sinica, 2011, 31(7):0733001(朱明, 刘真, 陈广学. 基于分区纽阶堡方程的6色印刷分色模型研究[J]. 光学学报, 2011, 31(7):0733001) |
| [9] | Yan Aiguo. Research on Neugebauer Multi-color Separation Based on Double Subarea Modification[D]. Nanjing:Nanjing Forestry University, 2012(严爱国. 基于双分区修正的纽介堡多色分色研究[D]. 南京:南京林业大学, 2012) |
| [10] | Wang Yifeng, Zeng Ping, Wang Ying. Multi-channel Printer Characterization Based on Gamut Partition[J]. Acta Electronica Sinica, 2010, 38(3):507-511(王义峰, 曾平, 王莹. 基于色域划分的多通道打印机色彩校正[J]. 电子学报, 2010, 38(3):507-511) |
| [11] | Wang B, Xu H, Luo M R, et al. Maintaining Accuracy of Cellular Yule-nielsen Spectral Neugebauer Models for Different Ink Cartridges Using Principal Component Analysis[J]. JOSA A, 2011, 28(7):1 429-1 435 |
| [12] | Urban P, Grigat R R. Spectral-based Color Separation Using Linear Regression Iteration[J]. Color Research & Application, 2006, 31(3):229-238 |
 2015, Vol. 40
2015, Vol. 40



