文章信息
- 张凯, 赵建虎, 张红梅
- ZHANG Kai, ZHAO Jianhu, ZHANG Hongmei
- 一种基于M估计的水下地形抗差匹配算法
- Robust Underwater Terrain Matching Navigation Based on M Estimation
- 武汉大学学报·信息科学版, 2015, 40(4): 558-562
- Geomatics and Information Science of Wuhan University, 2015, 40(4): 558-562
- http://dx.doi.org/10.13203/j.whugis20130011
-
文章历史
- 收稿日期:2013-04-07
2. 山东科技大学测绘科学与工程学院, 山东 青岛, 266590;
3. 武汉大学动力与机械学院自动化系, 湖北 武汉, 430072
2. School of Geomatics, Shangdong University of Science and Technology, Qingdao 266590, China;
3. School of Power and Mechanical, Wuhan University, Wuhan 430072, China
水下地形匹配是一种较好的水下辅助导航手段[1]。 在辅助INS导航过程中,水下地形匹配的精度和可靠性是影响导航性能的一个重要因素。水下地形匹配导航在航测深数据信息量、匹配区海床地形变化特征显著程度等方面均影响匹配结果的精度和可靠性[2, 3, 4, 5]。地形变化复杂时,匹配结果可靠性高;但当匹配区地形相似度较高时,匹配结果易出现误匹配,降低了匹配导航解的稳健性。针对这一问题,不少学者开展了相关研究[4, 5, 6],Nygren[4]提出通过航行较长路线或基于面海床信息获取技术,增加地形匹配中观测量,降低误匹配出现的概率,同时使用误匹配诊断方法来剔除潜在的误匹配结果的方法,实现稳健可靠的地形匹配导航。然而,受测深设备性能、测深过程中浮游物等因素的影响,在航测深数据中常伴随有粗差或渐进性系统误差。对于连续分布异常,现有滤波方法及基于人机交互的滤波方法均难以很好地判别该异常为实际地形还是异常测深;此外,受海流、潮汐潮流等因素的影响,局部海床地形可能发生变化,致使当前海床地形与已有海底地形模型存在差异。这些均改变了地形匹配中随机噪声模型的特点,可能导致匹配结果错误[4]。针对该问题,本文从稳健估计角度出发,提出一种基于M估计的抗差匹配算法,以期削弱海床地形模型和在航测深数据中粗差对水下地形匹配的影响,提高匹配导航解的稳健性。 1 水下地形导航算法原理
水下地形匹配首先根据当前位置信息,基于一定的误差估计(如4 σ准则),概略框定匹配搜索区;然后借助一定的匹配算法(如相关匹配算法),通过遍历、比较地形观测值和海床地形模型,将最为相似的位置作为载体当前位置。
匹配导航的函数模型可描述为[6]:
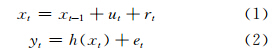
式中,rt~N(0,σt)为传递噪声;et为测量噪声。
式(2)为高斯-马尔柯夫(GM)模型。式中,h(xt)代表当前位置估值xt在地形模型h(·)中对应的水深值;et表示yt的测量噪声,通常为白噪声,et~N(0,σe)。当t时刻有多个地形观测值{yit,i=1,…,N},且观测值的协方差矩阵为 C 时,该时刻载体位置xt基于yt的极大似然估计为:

式中,矩阵 C 通常为对角阵,其对角线上的元素为观测值所对应的观测方差。式(3)表明,GM模型下,位置xt的极大似然估计与最小二乘估计一致,此时的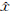 ML将具有最优统计性质,为最优线性无偏估计。
ML将具有最优统计性质,为最优线性无偏估计。
当单次地形匹配中地形测量值数量N较大时,地形匹配结果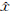 ML趋近于高斯分布[4]。
2 基于 M估计的地形匹配算法
ML趋近于高斯分布[4]。
2 基于 M估计的地形匹配算法
当数据中存在粗差时,最小二乘估计将会产生极大偏差。为消除该问题带来的影响,给出一种基于稳健M估计的抗差水下地形匹配算法。
稳健统计学认为粗差的出现是由于理想正态分布受到了污染或干扰,此时的误差真实分布用污染分布来描述[7]:
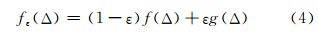
式中,ε为污染率,即粗差出现的概率;f(Δ)为理想情况下的正态分布;g(Δ)为粗差分布函数。
式(4)中,某种估计所能承受的ε越高,则该估计越稳健。统计学理论用ε的最大值作为衡量算法稳健性的标准,并把这一最大值称为崩溃点值。当数据中不含粗差时,估计方法的结果越接近最小二乘估计,则该方法的效率越高。统计学理论使用渐进效率来衡量稳健估计的有效性。
在进行最小二乘估计时,需要最小化的目标函数为:
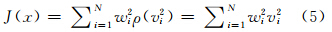
式中,vi为对应于第i个观测值的估计残差,所对应的崩溃点值为1/N,而渐进效率为1。
在稳健估计中,相应的目标函数则改为增长速度较慢的ρ函数,以牺牲一部分渐进效率为代价,提高估计结果的稳健性。为了提高匹配算法的抗差性和匹配结果的稳健性,采用Huber型ρ函数作为地形匹配结果稳健性的判断函数[7]:
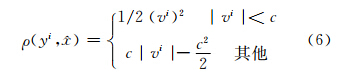
Huber型ρ函数是一个连续对称的凸函数,其一阶导函数表示为:
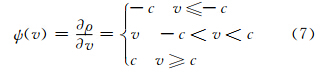
基于Huber型ρ函数的估计称为M估计。M估计在有效限制粗差影响的同时,对高斯分布噪声有较高的估计效率(当取c=1.57时,Huber型ρ函数对应的渐进效率达到最小二乘估计的95%)。M估计所对应的目标函数为非线性函数,必须使用数值计算方法进行迭代计算,本文采用迭代加权最小二乘法(IRLS)来进行计算[8]。
IRLS通过残差vi的幅度来调整权值wi0,以降低粗差的权重。因此初值的选择十分关键。如果直接使用最小二乘估计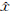 LS作为初值
LS作为初值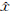 0,由于粗差会在
0,由于粗差会在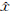 LS中产生蒙影(mask)效果,即残差vi最大的位置不一定是粗差的位置,则IRLS的计算结果仍不稳健。为此,本文以残差平方中位数最小(least median of squares,LMS)作为评判准则,对初始匹配位置
LS中产生蒙影(mask)效果,即残差vi最大的位置不一定是粗差的位置,则IRLS的计算结果仍不稳健。为此,本文以残差平方中位数最小(least median of squares,LMS)作为评判准则,对初始匹配位置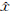 0进行估计[9]。
0进行估计[9]。
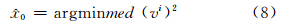
LMS估计具备较高的稳健性,其崩溃点值接近0.5。 LMS估计效率虽相对较低,但非常适合用于粗差探测[10]。
若yi为水深观测值,j为迭代次数,则基于M估计的抗差水下地形匹配步骤如下。
1) 借助实测地形数据和框定的搜索区背景海床地形数据,开展首次匹配,根据式(8)估计载体位置 x的初值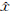 0;
0;
2) 利用初值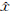 0计算各观测值yi的残差vi0=yi-h(x0)i,进而计算权值:
0计算各观测值yi的残差vi0=yi-h(x0)i,进而计算权值:
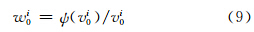
3) 根据迭代式
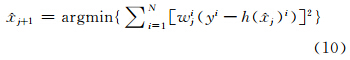
重新进行地形匹配,计算匹配位置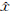 j+1;
j+1;
4) 重复步骤2)~3),直至相邻两次迭代计算的载体位置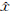 n和
n和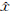 n+1满足设定的限差ε为止。
自此,获得了载体当前或然位置:
n+1满足设定的限差ε为止。
自此,获得了载体当前或然位置:

以上算法借助式(6)中的Huber型ρ函数实施定权约束,式(9)实施位置确定加权控制。对于测量或地形模型因素引起的较大残差,通过反复迭代不断约束其权值,削弱其在载体位置确定中的影响,确保了最终载体位置确定的稳健性,提高了匹配解的抗差性。 3 误匹配的检验
Nygren指出[4],水下地形匹配中,当潜航器航行于地形变化特征区时,随着测深数据量的不断增加,匹配结果的概率分布趋近于高斯分布(图 1(a)),误匹配出现的几率将以指数速度下降;但当载体航行于海床变化平缓区、相似区或贫特征区时,因匹配精度接近,遍历匹配结果中常会出现多个峰值(图 1(b)),进而导致匹配结果可能存在多解性,甚至误匹配。为此,Nygren提出通过构建式(12)的概率统计量ξ来判断误匹配:
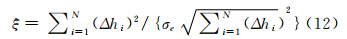
式中,Δhi为相似地形之间的地形差异。
 |
| 图 1 单峰和多峰概率分布Fig. 1 Probability Distribution (Single Peak and Multimode) |
当误匹配的概率ξ大于指定阈值时,将不使用本次匹配结果进行量测更新。
在基于M估计的稳健地形匹配中,将式(12)相应调整为:
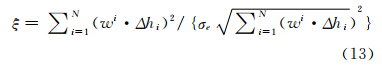
式中,wi为由式(9)计算得到第i个观测值所对应的权值。 4 实验结果及分析
为了验证本文所述方法的有效性,以渤海湾 某水域多波束测深实测数据为背景场(图 2),进行仿真实验。实验背景区域为面积3 km × 7 km的实测海底地形。水下载体航迹由图 2中黑色曲线表示,航迹由A点出发,到B点结束。在航行过程中,载体每隔60 m使用多波束测深系统进行海底地形测量,声呐系统的波束数为121,同时通过压力深度仪测量载体深度。在仿真中,声呐中的测量误差设置为测量距离的1%,,背景场地 形图噪声误差水平设为0.2 m,深度仪测量误差 设为水深的0.3%。INS中的漂移误差设为航行距离的1%,载体在水平方向上的搜索半径设置为50 m。
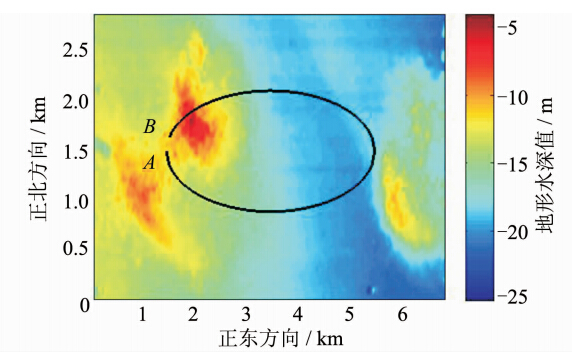 |
| 图 2 实验区域水下地形背景场及实验航迹Fig. 2 Background Seabed Terrain and Sailing Track |
1) 背景地形和测深观测数据中均不含粗差
分别使用传统相关匹配算法和本文抗差匹配算法,沿航迹进行匹配实验,两种算法的匹配误差分布如图 3(a)所示。可以看出,两种方法的匹配结果误差分布基本一致,匹配误差均值分别为4.72 m和5.06 m。
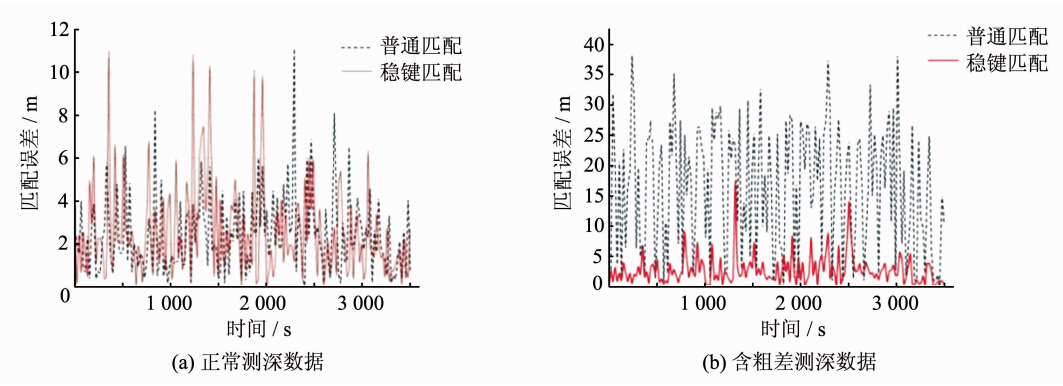 |
| 图 3 正常测深和含粗差测深数据情况下两种方法匹配误差比较Fig. 3 Two-method Matching Errors with Normal Data and Abnormal Data |
2) 测深观测数据中含有粗差
在测深观测数据中附加污染率为5%,大小为0.5 m的粗差,然后沿航迹匹配,两种匹配算 法匹配误差分布如图 3(b)所示。在此种污染水平下,粗差对测量值的均值和方差影响较小。以某历元测量值为例,正常测量值的均值和标准差分别为-0.02 m和0.26 m,添加粗差后为0.01 m和0.28 m。添加粗差后传统匹配算法匹配结果受到严重影响,而本文方法却取得了较好的匹配精度。
3) 背景地形模型中含有粗差
为搜索区地形模型附加污染率为5%,大小为0.5 m的粗差,沿航迹地形匹配,两种方法匹配结果如图 4(a)所示。
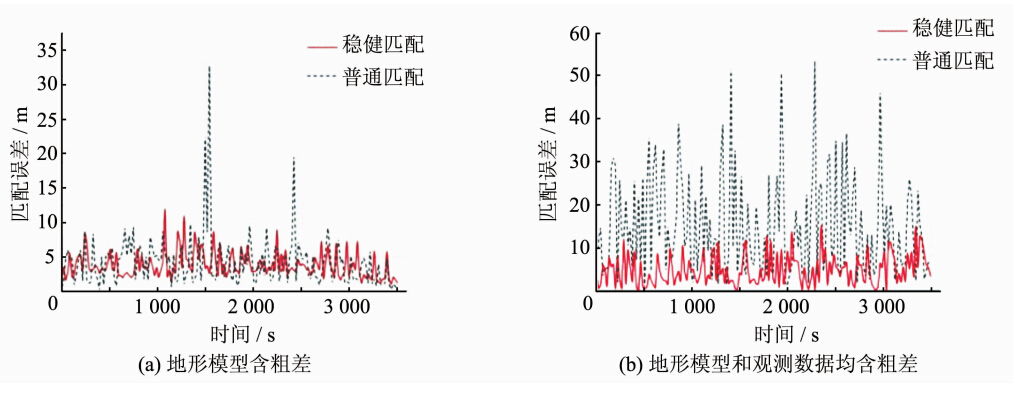 |
| 图 4 地形模型含粗差时与地形模型和观测数据均含粗差时两种算法结果比较Fig. 4 Impacts of Outliers in the Terrain Map and Both Measurement and the Terrain Map |
可以看出,稳健地形匹配仍然表现出了良好的抗差性,而传统地形匹配算法结果出现了较大匹配误差,但是其受影响程度明显小于图 3(b)中情况。这是由于当粗差在搜索范围内随机分布时,其出现于真实匹配位置的几率相对较小,因此对地形匹配的影响较观测数据要小得多。而当粗差出现于地形观测值中时,由于作为匹配标准的地形观测值已经严重背离了真实地形,因此匹配位置会受粗差的影响在搜索范围内随机漂移。但当粗差出现在载体真实位置对应的背景地形时,匹配结果会被粗差“挤压”到真实位置附近不含粗差且与真实位置对应地形最相近的区域。而稳健地形匹配算法中,由于含有粗差的观测值或者背景地形值在匹配过程中被降权,削弱了粗差对匹配结果的影响。
4) 地形模型和测深观测数据中均含粗差
为测深观测数据和搜索区地形模型附加污染率为5%,大小为0.5 m的粗差,沿航迹地形匹配,两种方法匹配结果如图 4(b)所示。可以看出,稳健匹配算法和传统匹配算法的匹配结果与图 3(b)相似,但传统算法匹配结果表现出了很强的波动性,稳健匹配算法则受粗差的影响不明显。
为了比较不同情况下粗差对不同算法匹配结果的影响,将粗差污染率固定为5%,大小为0.5 m时,对两种算法匹配结果进行统计,结果如表 1所示。
| 数据 | 匹配方法 | Max/m | Min/m | Mean/m | STD/±m |
| 背景和实测数据正常 | 传统 | 11.10 | 0.42 | 4.72 | 3.35 |
| 稳健 | 11.01 | 0.14 | 5.06 | 3.17 | |
| 实测数据中含有粗差 | 传统 | 70.71 | 1.09 | 21.09 | 10.09 |
| 稳健 | 16.51 | 0.57 | 5.39 | 2.76 | |
| 背景地形数据中含有粗差 | 传统 | 32.71 | 0.19 | 6.73 | 3.84 |
| 稳健 | 12.01 | 1.08 | 5.16 | 1.96 | |
| 背景和实测数据均含有粗差 | 传统 | 53.25 | 0.85 | 17.93 | 11.45 |
| 稳健 | 14.39 | 0.85 | 5.27 | 3.59 |
从表 1中可以看出,污染率一定时,地形观测数据中粗差对匹配结果的影响较显著;无论哪种情况下,本文算法均取得了较好的匹配结果。
增加地形测量值中的粗差比例,提高数据污染率,基于本文算法开展匹配实验,给出不同污染 率下的地形匹配精度,如图 5所示。从图 5可以看出,随着污染率的增加,稳健地形匹配算法匹配结果的均方根误差也随之增加,但即使观测数据污染率达到45%,匹配算法仍可以给出具有较高精度的匹配定位结果,进一步证明该匹配算法的稳健性。
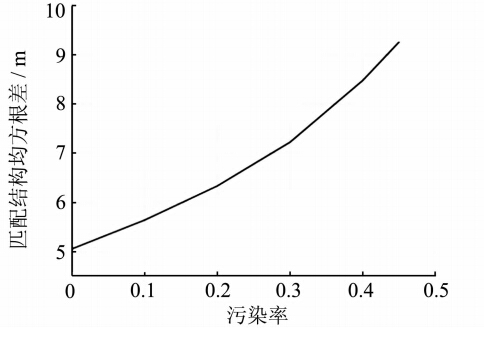 |
| 图 5 污染率与地形匹配精度关系图Fig. 5 Variation of Accuracy when Contamination Rate Changes |
在水下地形匹配辅助导航中,地形测量值和地形模型中的粗差(异常值)会引起错误的地形匹配结果,进而影响辅助导航的精度和可靠性。本文基于M估计,给出一种稳健地形匹配算法,具有较好的抗差性,显著削弱了粗差对地形匹配结果的影响,提高了匹配解的精度和可靠性,并得到了仿真实验的验证。
| [1] | Zhang Feizhou, Lv Wenfang. Simulation Research on Matching Algorithm of Autonomous Underwater Navigation System[J]. Geomatics and Information Science of Wuhan University, 2003, 28(2):153-157 (张飞舟, 侣文芳. 水下无源导航系统仿真匹配算法研究[J]. 武汉大学学报·信息科学版, 2003, 28(2):153-157) |
| [2] | Zhao Jianhu, Wang Shengping, Wang Aixue. Study on the Selection of the Geomagnetic Adaptable Matching Area Based on the Geomagnetic Co-occurrence Matrix[J]. Geomatics and Information Science of Wuhan University, 2011, 36(4):235-239 (赵建虎, 王胜平, 王爱学. 基于地磁共生矩阵的水下地磁匹配适配区选择[J]. 武汉大学学报·信息科学版, 2011, 36(4):235-239) |
| [3] | Bergman N, Ljung L. Terrain Navigation Using Bayesian Statistics[J]. Control Systems, IEEE, 1999, 19 (3):33-40 |
| [4] | Nygren I, Jansson M.Terrain Navigation for Underwater Vehicles Using the Correlator Method[J]. IEEE Journal of Oceanic Engineering, 2004, 29:906-915 |
| [5] | Anonsen K B. Advances in Terrain Aided Navigation for Underwater Vehicles[D]. Norway:Norwegian University of Science and Technology, 2010 |
| [6] | Meduna D K. Terrain Relative Navigation for Sensor-limited Systems with Application to Underwater Vehicles[D].USA:Stanford University, 2011 |
| [7] | Huber P J, Huber P, Statisticien M, et al. Robust Statistical[M]. New York:Wiley, 1981 |
| [8] | Street J O, Carroll R J, Ruppert D.A Note on Computing Robust Regression Estimates via Iteratively Reweighted Least Squares[J]. The American Statistician, 1988, 42:152-154 |
| [9] | Rousseeuw P J. Least Median of Squares Regression[J]. Journal of the American Statistical Association, 1984, 79:871-880 |
| [10] | Gandhi M A, Mili L. Robust Kalman Filter Based on a Generalized Maximum-likelihood Type Estimator[J]. IEEE Transactions on Signal Processing, 2010, 58 (5):2 509-2 520 |
 2015, Vol. 40
2015, Vol. 40


