文章信息
- 何海清, 黄声享, 陈婷
- HE Haiqing, HUANG Shengxiang, CHEN Ting
- 一种顾及粗差的径向神经网络高程曲面拟合法
- Gross Error Considered Height Surface Fitting Using Radial Neural Network
- 武汉大学学报·信息科学版, 2015, 40(4): 547-551
- Geomatics and Information Science of Wuhan University, 2015, 40(4): 547-551
- http://dx.doi.org/10.13203/j.whugis20130041
-
文章历史
- 收稿日期:2013-04-11
2. 武汉大学测绘学院, 湖北 武汉, 430079;
3. 武汉大学水利水电学院, 湖北 武汉, 430072
2. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China;
3. School of Water Resources and Hydropower, Wuhan University, Wuhan 430072, China
高程曲面拟合法对建立数字高程模型来说至关重要。研究者提出了许多拟合数学模型,常用的具有代表性的模型主要包括多项式曲面拟合、多面函数法曲面拟合、移动法曲面拟合和神经网络拟合模型等。其中,神经网络高程拟合的研究较为广泛,张昊等[1]验证了神经网络拟合高程比常用的二次多项式曲面拟合法精度高、效果好;缪报通等[2]从应用结果证实径向神经网络方法适用于解决曲面离散点集的光滑插值,且比传统样条方法更优;宋雷等[3]研究神经网络拟合大地水准面;张正禄等[4]利用神经网络对监测点位移进行建模;何海清等[5]通过比较分析验证了利用径向神经网络能对大坝碾压摊铺层高程进行高精度拟合等。径向神经网络(radial basis function neural network)拟合的高程曲面经过所有的高程训练样本点,是精确的拟合方法,但由于其进行高程曲面拟合时未顾及粗差的影响,若存在粗差,可能影响整个拟合精度。
本文提出了顾及粗差的径向神经网络高程曲面拟合法。该方法首先通过径向神经网络拟合含粗差高程点,并将各格网点程映射到影像的灰度值,引入高斯差分( Difference of Gaussian,DoG)极值检测法与最小二乘移动曲面拟合法来探测与修正粗差,然后再次对粗差修正后的高程样本点进行径向神经网络拟合,取得了比未顾及粗差的径向神经网络拟合法更优的精度和较理想的拟合结果。 1 顾及粗差的径向神经网络高程曲面拟合 1.1 径向神经网络原理
径向神经网络是一种利用径向基函数(radial basis functions,RBF)作为激活函数的人工前向神经网络,包括输入层、非线性RBF激活函数的隐含层、线性输出层等。如图 1所示,输入层模型化为一个实数向量X∈RD,输出层为输入向量的标量函数f:RD→R。
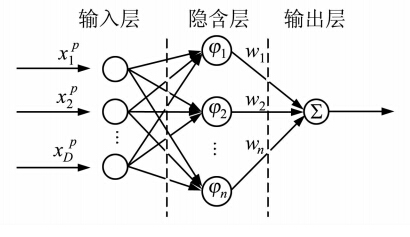 |
| 图 1 RBF神经网络原理图Fig. 1 Principle of RBF |
在多维空间n个数据点的精确插值中,每一数据点都需有D维的输入矢量xp= xpi:i=1,…,D 映射到对应的目标输出tp,目标函数为:
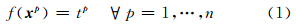
在RBF方法中,各数据点对应n个基函数φ ‖x-xp‖ ,φ · 为线性函数,‖x-xp‖表示数据点x与第p个数据点xp的欧氏距离。输出函数f(x)为一系列RBF函数的加权线性组合,其函数表达式为[6]:
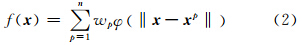
式中,wp为各数据点的权值,则第q点的插值表达式为:
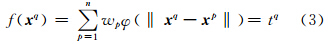
令向量t={tq},w ={wp},Φ ={φ(‖xq-xp‖)},则式(3)可简化为:

式中,若Φ为可逆矩阵,则权矩阵 w 解算表达式为:

当权值求出后,f(x)的 值表示连续的拟合曲面。RBF主要包括高斯函数、复二次函数、薄板样条函数等。本文采用复二次函数作为径向基函数拟合高程,可获得较好的拟合效果[5, 7]。若Φ不为方阵,则无法利用式(5)解出权矩阵,因此,采用权值学习简单、整体性较强[6]的梯度下降算法来求解权值。定义权值目标函数为:
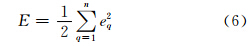
式中,eq为输入第q个样本时的误差;设yq为第q个样本期望输出值,定义
eq=yq-f(xq)=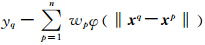 ),权值的调整公式为:
),权值的调整公式为:
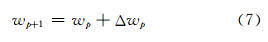
式中,
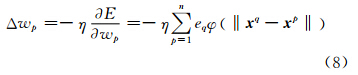
式中,η为学习速率(0<η<1),通过迭代运算直至E收敛求出权值。 1.2 粗差探测与修正
不存在粗差时,径向神经网络拟合法可获得较高精度的高程曲面[5];若训练样本数据中存在粗差,曲面也将经过粗差点,因而粗差结果可能影响高程曲面精度。在常用的方法中,直接利用格网点高程值即可进行粗差分析;然而,由于高程样本点可能是不规则数据,采用一定范围内或一定数量的邻近高程点数据来分析粗差,粗差探测结果会因高程数据结构的不同而有所差异。文献[8]针对规则或不规则的高程样本点数据,提出了相应的曲面拟合方法,但没有同时较好兼容这两种数据结构的方法。为使高程曲面拟合对不同结构的样本点数据具有更强的适应性,本文将径向神经网络拟合的曲面格网高程转换为影像来处理,相应的高程值映射到影像灰度值,高程曲面范围内数据都转化为规则的影像栅格灰度值。粗差点在影像以灰度作为z值的三维显示中表现为明显的尖峰或凹陷即局部极大值。 在i行j列,高程值Zi,j与影像灰度值gi,j映射关系为:
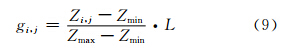
式中,Zmax、Zmin分别为高程最大与最小值;L为影像灰度等级,一般为8 bit影像即L=255(灰度值范围为0~255)。粗差点在局部高程异常,破坏了地形表面的连续性,与周围高程点形成较大的反差,成为特征点[9],因此可通过特征点检测方法来探测粗差点,将粗差点视为噪声。
由于径向神经网络拟合曲面中的粗差点在灰度影像中灰度值会发生剧烈变化,这些特征点具有很好的稳定性和抗干扰性,利用DoG极值检测法可检测出这类特征点[10]。因此,本文采用DoG极值检测算法在一定尺度范围内搜索粗差点。该算法可增强特征,通过锐化高频信息增强数字影像的边缘和细节。由于粗差点类似噪声,为高频信息,DoG后会增强噪声,有利于稳健地检测出粗差点位。DoG的计算公式为:
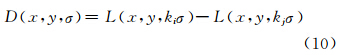
式中,L x,y,kσ 为原始影像I x,y 在尺度参数为kσ的高斯函数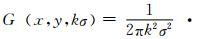
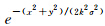 窗口内的卷积运算,即
窗口内的卷积运算,即

式中,表示卷积。
如图 2所示,在DoG内提取各像素局部3×3窗口内的极值点,判断该窗口中心像素是否是极值点(极大值或极小值),从而确定特征点。
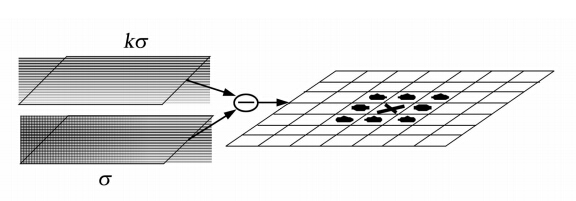 |
| 图 2 DoG局部极值检测Fig. 2 Peaks Detection from DoG |
为了进一步精化极值点在影像中的空间位置,需对空间函数D (x,y,σ) 进行泰勒二次展开,采用二次曲面拟合法解算极值点坐标的修正量,从而实现对已检测到的极值点位置精化。D (x,y,σ)泰勒展开式为:
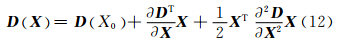
式中,X = (x,y,σ) T为极值点坐标的修正向量;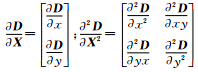 。对式(12)求导计算极值点修正量 为:
。对式(12)求导计算极值点修正量 为:
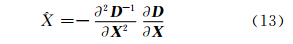
将 代入式(12)可得:
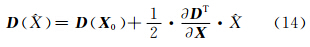
若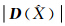 小于给定的阈值DT,则剔除该极值点。极大值点对周围局部高程值的影响半径r计算公式为:
小于给定的阈值DT,则剔除该极值点。极大值点对周围局部高程值的影响半径r计算公式为:
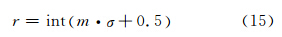
式中,int表示取整;σ为影像的初始尺度,常取值为1.6。极值点周围所有点灰度均值 与中误差gstd.表达式为:
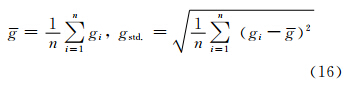
以高斯差分极值点为中心,m以固定步长1(即m0=3,m1=m0+1,m2=m0+2,…)增加半径r,若在增加范围内(即环形区域)的灰度均值go与中误差gstd° .满足:
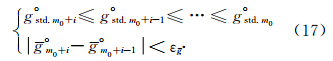
式中,m0,…,m0+i-1,m0+i每一步长内(即环形区域)的灰度中误差g° std.趋向收敛,且相应的均值g° m0+i与 g° m0+i-1之差小于阈值ε °,则终止扩大范围确定半径r=int m0+i ·σ+0.5 。
在半径r内,若极值点的灰度值g的残差gresidual= g-g>k·gstd.(k常取值为3,即3倍中误差)时,则把该极值点视为粗差点。
为修正粗差点位样本高程值,避免其对周围高程点插值时产生的“污染”,选取半径r范围内局部窗口的数据点,采用最小二乘移动曲面函数插值来修正样本点高程:
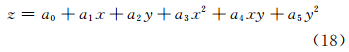
式中,z为高程值;ai为待定参数;(x,y)为数据点坐标。列出误差方程:

式中,V = [v1 v2 … vn] T(n为半径r范围内的高程训练样本点数);X为待定参数矩阵;
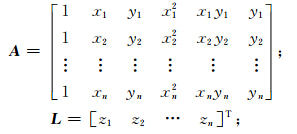
利用间接平差列法方程求出式(19)的最小二乘解:
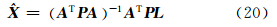
式中,P为单位权矩阵。
在粗差点位以移动曲面插值得到高程值替换该点位邻近的高程训练样本点,进而修正原始样本点高程粗差,然后再次利用径向神经网络对粗差修正后的高程样本点进行曲面拟合,实现可抵抗粗差的高程曲面拟合。 2 实验结果及分析
为验证本文高程拟合算法的有效性,采用Leica TCA2003测量机器人实测的连续表面离散高程点数据进行实验,共有1 200个三维坐标数据点,高程z值范围为288~293 m,区域大小为300×300 m。为了便于对比分析,对该数据加入若干粗差,用径向神经网络和本文算法对含粗差的数据点进行高程拟合。同时,利用径向神经网络对无粗差的数据点进行高程拟合,三种方法高程拟合曲面见图 3~5。含有粗差的情况下,径向神经网络拟合的高程曲面有一些毛刺、尖峰和凹陷,表面不光滑,与无粗差径向神经网络拟合的曲面有明显差异,抵抗粗差能力较弱;而本文算法拟合的高程曲面较为连续、平滑,无明显尖峰或凹陷,与无粗差径向神经网络拟合的曲面较为接近。采用15个实测高程数据点作为检核点评估本文算法的精度(表 1)。含粗差径向神经网络拟合的精度为0.38 m,最大残差0.85 m,外符合精度远低于无粗差时高程拟合精度,仅为其1/2.5,而本文算法精度为0.16 m,最大残差为0.35 m,与无粗差高程拟合精度较为接近,可见本文高程曲面拟合法能探测与剔除粗差,得到了较为理想的拟合结果和较高的精度。
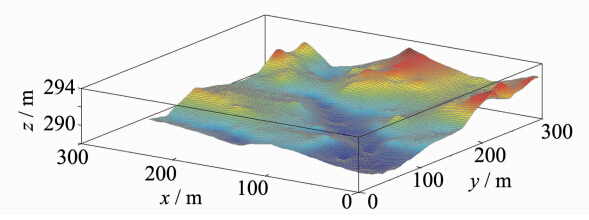 |
| 图 3 径向神经网络拟合(无粗差)Fig. 3 Radial Neural Network in Height Fitting Without Gross Error |
| 检核点 | 无粗差点 | 含粗差点 | |
| 径向神经网络 | 径向神经网络 | 本文算法 | |
| ck1 | -0.05 | 0.16 | -0.07 |
| ck2 | 0.11 | 0.27 | 0.09 |
| ck3 | 0.08 | 0.85 | 0.10 |
| ck4 | 0.13 | -0.25 | 0.12 |
| ck5 | -0.21 | -0.29 | -0.22 |
| ck6 | 0.07 | 0.31 | 0.12 |
| ck7 | -0.05 | -0.17 | -0.09 |
| ck8 | -0.14 | -0.43 | -0.17 |
| ck9 | -0.12 | 0.19 | -0.12 |
| ck10 | 0.31 | 0.44 | 0.35 |
| ck11 | 0.22 | 0.72 | 0.19 |
| ck12 | -0.03 | -0.1 | -0.10 |
| ck13 | 0.07 | 0.18 | 0.08 |
| ck14 | 0.17 | 0.11 | 0.15 |
| ck15 | 0.20 | 0.33 | 0.21 |
外符合精度: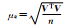 | 0.15 | 0.38 | 0.16 |
| 注:v=z检核点-z拟合点。 | |||
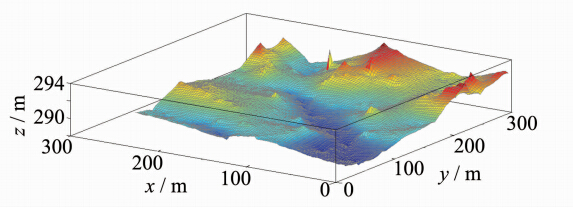 |
| 图 4 径向神经网络拟合(含粗差)Fig. 4 Radial Neural Network in Height Fitting with Gross Error |
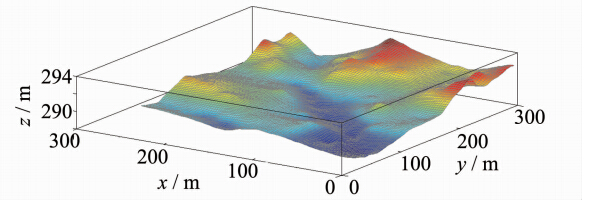 |
| 图 5 本文方法(含粗差)Fig. 5 Robust Radial Neural Network in Height Fitting with Gross Error |
径向神经网络高程拟合曲面经过所有训练样本点,对于无粗差存在的情况,径向神经网络高程拟合法可得到较为理想的高程曲面,但对于粗差,抵抗能力较弱。本文通过影像高斯差分算法探测粗差,结合最小二乘移动曲面法修正粗差值,进而利用径向神经网络拟合高程。通过Leica TCA2003实测数据进行拟合实验,高程拟合曲面的外符合精度为0.16 m,与无粗差高程拟合精度相近,明显减小了粗差对拟合产生的影响,能抵抗训练样本点中粗差的干扰,具有较强的可靠性和实用性。
| [1] | Zhang Hao, Wang Qijie, Zhu Jianjun, et al. Influence of Sample Data Preprocessing on BP Neural Network-based GPS Elevation Ftting[J]. Journal of Geodesy and Geodynamics, 2011, 31(2):125-128(张昊, 王琪洁, 朱建军, 等. 样本数据预处理对基于BP神经网络的GPS高程拟合的影响[J]. 大地测量与地球动力学, 2011, 31(2):125-128) |
| [2] | Miao Baotong, Chen Falai. Application of Radius Basis Function Neural Networks in Scattered Data Interpolation[J]. Journal of China University of Science and Technology, 2001, 31(2):135-142(缪报通, 陈发来. 径向基函数神经网络在散乱数据插值中的应用[J]. 中国科学技术大学学报, 2001, 31(2):135-142) |
| [3] | Song Lei, Fang Jian, Zhou Xuhua, et al. Application of Bayesian Regulation BP Neural Network Tofit Two Kind Quasigeoid[J]. Geomatics and Information Science of Wuhan University, 2009, 34(5):552-555 (宋雷, 方剑, 周旭华, 等. Bayesian正则化BP神经网络拟合两类似大地水准面[J]. 武汉大学学报·信息科学版, 2009, 34(5):552-555) |
| [4] | Zhang Zhenglu, Wang Xiaomin, Deng Yong, et al. Application of Fuzzy Neural Network in Deformation Analysis and Prediction[J]. Geomatics and Information Science of Wuhan University, 2010, 35(1):7-8(张正禄, 王小敏, 邓勇, 等. 模糊神经网络在变形分析与预报中的应用研究[J]. 武汉大学学报·信息科学版, 2010, 35(1):7-8) |
| [5] | He Haiqing, Huang Shengxiang, Wu Gen. Height Fitting by Radial Neural Network for the Construction Quality Control of Face Rockfill Dam[J]. Geomatics and Information Science of Wuhan University, 2012, 37(5):594-597(何海清, 黄声享, 伍根. 碾压施工质量监控的径向神经网络拟合高程研究[J]. 武汉大学学报·信息科学版, 2012, 37(5):594-597) |
| [6] | Marcek M, Marcek D. Granular RBF Neural Network Implementation of Fuzzy Systems:Application to Time Series Modeling[J]. Multiple-Valued Logic and Soft Computing, 2008, 14(3/5):401-414 |
| [7] | Tang Zesheng. Visualization of 3D Data Field[M].Beijing:Tsinghua University Press, 1999(唐泽圣. 三维数据场可视化[M]. 北京:清华大学出版社, 1999) |
| [8] | Yang Xiaoyun, Gu liya, Cen Minyi, et al. A Method Based Fitting of Moving Quadric Surface with Variable Windows for Detecting Gross Errors in Irregular DEM[J]. Acta Geodaetica et Cartographica Sinica, 2005, 34(2):148-153(杨晓云, 顾利亚, 岑敏仪, 等. 基于不同大小窗口的移动曲面拟合法探测不规则DEM粗差的一种方法[J]. 测绘学报, 2005, 34(2):148-153) |
| [9] | Shan Jie. An Interactive Method for Blunder Detection in DEM Data[J]. Journal of PLA Institute of Surveying and Mapping, 1993, 2:28-31(单杰. 一种交互式DEM粗差检测方法[J]. 解放军测绘学院学报, 1993, 2:28-31) |
| [10] | Lowe D G. Object Recognition from Local Scale- Invariant Features[C]. The IEEE International Conference on Computer Vision, Kerkyra, Greele, 1999 |
 2015, Vol. 40
2015, Vol. 40


