文章信息
- 于男, 程鹏飞, 成英燕
- YU Nan, CHENG Pengfei, CHENG Yingyan
- 基于地表负载一阶变化反演季节性地球形变
- Seasonal Earth Deformation from the Change of the Degree-1 Surface Mass Load
- 武汉大学学报·信息科学版, 2015, 40(4): 540-546
- Geomatics and Information Science of Wuhan University, 2015, 40(4): 540-546
- http://dx.doi.org/10.13203/j.whugis20130367
-
文章历史
- 收稿日期:2014-10-15
2. 中国测绘科学研究院, 北京, 100830;
3. 国家测绘产品质量检验测试中心, 北京, 100830
2. Chinese Academy of Surveying and Mapping, Beijing 100830, China;
3. National Quality Inspection and Testing Center for Surveying and Mapping Products, Beijing 100830, China
在漫长的时间里,地球表面液体层的质量是守恒的,其在地表的再分布周期从1 d~1 a不等,与地球的自转(来自太阳的热量驱使大气)和公转(每年的全球水循环)相关[1]。对于一个弹性地球来说,地表液体层的质量再分布势必会引起固体地球的形变[2]。从全球范围来看,如果地表液体层由于季节性循环主要集中在北半球,导致北半球的负载增加,则北半球被挤压,南半球扩张,反之亦然,这就是季节性地球形变的原因。
目前,对于弹性地球形变的研究,传统上习惯使用Farrell的表面负荷理论即负载勒夫数理论。该理论广泛应用于大气层和水体等负载模型的理论建模中。1972年,Farrell首次对弹性地球进行建模,阐述了地球的形变响应是由地表负载所引起的引力位变化的球谐分量的函数[3]。随着地球模型研究的不断深入和完善,SNREI模型逐渐成为人们普遍接受的“标准地球模型”。在这个模型下,地球是对称、非旋转、完全弹性和各向同性的,当其表面负载发生变化的时候,固体地球会产生静态形变[4, 5]。Blewitt首次利用地表引力位一阶球谐分量的变化和负载勒夫数理论,通过GPS数据反演得到了季节性的地球形变[6]。孙付平等利用GPS和VLBI组合的站坐标、站速度,采用Delaunay算法生成的三角形来逼近地形表面,研究了地球的表面积、体积及它们的变化趋势。结果表明,目前地球半径每年大约缩短3~4 mm,地球整体上处于压缩变形中[7, 8]。申文斌等基于ITRF2000框架的671个台站,利用同样的方法研究得到地球目前正处于南胀北缩的状态中,但地球整体处于膨胀状态[9]。此外,夏一飞等研究了日月引潮力以及变化着的地球自转惯性离心力的作用下所产生的地球周期性弹性形变[10];徐建桥等研究了地球固体部分对液核动力学效应引发的核幔边界和内核边界上压力和引力扰动的形变响应[11]。 1 弹性地球形变与地球参考框架原点
国际地球参考框架的原点定义在整个地球系统的质量中心(CM),由于地球整体在惯性空间下不受外力作用,所以CM的位置并不会因为地球表面的质量再分布而产生变化,变化的是固体地球质量中心(CE)。虽然参考框架的原点定义在CM,但实际上却是通过与CE相差只有2%的固体地球外表面的几何中心(CF)来实现的[1, 2]地表质量再分布,CF框架点是由地球表面覆盖的统一的、无限多的点构成的,这些点的运动也需要考虑。实际上可以通过在全球建立合适密度的观测站来实现,使用GPS易于实现。
地表液体层质量再分布的过程会通过两种方式影响到大地测量网络:1)伴随地表质量再平衡的过程所产生的CE相对于CM的位移,即地心运动,其对ms级地球参考框架所造成的影响是不容忽视的[12];2)地表跟踪站本身伴随着固体地球形变而产生的位移[1, 12]。基于此,如果能够得到地表跟踪站的精确位置变化,应用相应的弹性地球负载模型,就可以探索固体地球的弹性形变机制。目前的研究表明,地表负载的一阶变化项与地表负载的质量中心和地心直接相关,而高阶项与负载的质量中心之间的关系尚不明确,所以本文只讨论一阶负载下的地球弹性形变。 2 负载力矩理论及其与弹性地球形变的关系 2.1 负载力矩的基本理论
由于整个地球系统在惯性空间下的运动是不受外力的,即满足动量守恒的条件,因此伴随地表质量再分布的过程有:
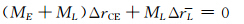
式中,ΔL是地表液体层的质量中心在CE框架下的位置变化;ML为地表液体层的质量;ME为固体地球的质量;则CE相对于CM的变化为:

负载力矩矢量被定义为:

应用“负载力矩”理论可以更加方便地研究地表负载变化驱使固体地球形变的机制。 2.2 负载力矩理论反演弹性地球形变的方法
由于地表质量再分布所引起的CE相对于CM的位置变化会导致地球表面引力位发生变化,其一阶分量的球谐函数可以表示为:

式中,Ω为地理位置(纬度φ,经度λ); (Ω)是径向单位向量; g 为地表重力加速度。式(2)是一个纯粹的球谐函数,可以直接应用负载勒夫数理论。根据负载勒夫数理论,CE框架下地球表面位移ΔSh(Ω)(径向),ΔSl(Ω)(切向)可以表示为:
<
(Ω)是径向单位向量; g 为地表重力加速度。式(2)是一个纯粹的球谐函数,可以直接应用负载勒夫数理论。根据负载勒夫数理论,CE框架下地球表面位移ΔSh(Ω)(径向),ΔSl(Ω)(切向)可以表示为:
<
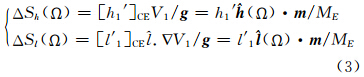
式中,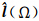 是切向单位向量;地表梯度算子
是切向单位向量;地表梯度算子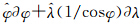 ;此处使用Farrell的负载勒夫数模型[4]:
;此处使用Farrell的负载勒夫数模型[4]:
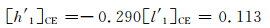
理论上,CF框架原点满足地球表面位移场的积分为0的条件,这与沿着各个轴向的投影的无网络变换是一致的。CE框架的最大不足之处在于它不可以被直接观测。而CF框架与CE框架特别近似,相比之下,CF框架更方便于实际观测[13],CE框架更适合于理论研究。若将CF框架与CE框架进行严格比较,则需要一个从CE框架到CF框架的坐标转换。根据Blewitt的负载勒夫数转换理论,CF框架下的负载勒夫数与CE框架下的负载勒夫数之间的关系为[2]:
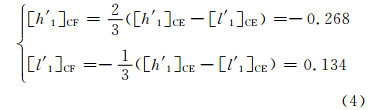
CF框架下地表某处点位位移(为了看起来更简洁,这里省略了Ω):

因此,CF框架下地表GPS测站的位移 [Δs]CF=(Δsx,Δsy,Δsz)T可以表示为:
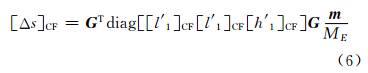
式中,G 是3×3维的将地心坐标转换为地面(东西、北南、垂直)坐标的雅可比矩阵:
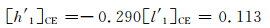
事实上,由于框架点全球分布的不均匀性,地球参考框架从本质上来说只是 CF框架的一个近似,实际上为CN(the center of network)框架,即由地面网实现的参考框架。利用GPS数据得到的[Δs]CF是CN框架下测站的形变,而式(6)直接采用的是CF框架下的负载勒夫数,这个误差可以通过附加平移参数t来减弱或消除[14]:

因此,通过计算全球范围内的GPS跟踪站的位移[Δ s]OBS,就可以通过式(7)计算得到“地表负载力矩” m ,进而探索固体地球形变规律;相反,如果地表负载变化能够被建模,我们也可以通过式(7)计算得到由于弹性地球形变而造成的测站位移。
2.3 最小二乘法的设计矩阵
根据式(7),其未知参数矩阵为:
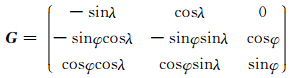
设计矩阵为:

国际 GNSS服务(IGS)每星期为用户提供精确的IGS跟踪站坐标及变化率,这为利用IGS数据探索固体地球形变提供可能。截至目前,IGS共有11个分析中心,GPS卫星跟踪网中共有856个跟踪站[15]。利用这些可靠的数据源,可以精确解算地表负载力矩,进而研究固体地球形变机制。本文选择IGS05框架的132个框架点(图 1),利用IGS重新处理得到的近10 a的igl周解数据[16](共522周),反演得到了近10 a地球表面负载力矩变化的时间序列(图 2)。图 2中mx、my、mz的方向与WGS-84定义的XYZ三轴方向一致,igl解在数据处理时根据阈值剔除了质量不好的测站,较为完善地考虑了各种突变,同时,igl解准确合理地消除了由板块运动、冰后回弹等引起的测站位置的长期变化,剔除了仪器变动和同震位移等引起的测站位置突变。
 |
| 图 1 IGS05框架的132个框架点Fig. 1 132 Sites of the IGS05 Reference Frame |
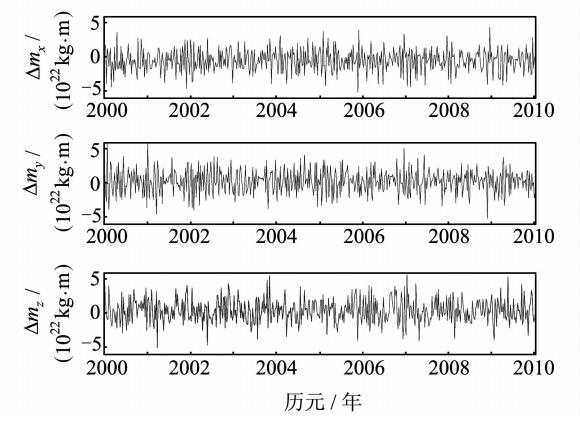 |
| 图 2 近十年地表负载力矩变化 Fig. 2 The Variations of Load Moment in Recent Ten Years |
为了计算负载力矩时间序列能量谱密度并确定其主要周期,对mx、my、mz序列分别进行傅里叶变换,得到其功率谱(图 3)。功率谱密度越大,说明该频率对负载力矩分量的贡献就越大,因此可由图 3确定负载力矩各分量的主频率。
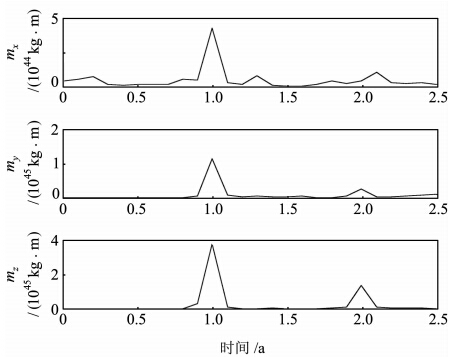 |
| 图 3 地表负载力矩时间序列的功率谱分析Fig. 3 The Power Spectrum Analysis of Load Moment Time Series |
计算分析表明:负载力矩各分量都有明显的年周期变化和相对较弱的长周期变化,mx方向有一个1.3 a和一个2.1 a的周期,my和mz均有一个2 a周期。由于反演的数据源采用的是周解,相当于采样率为一周,因此还不足以发现更短的周期。 4.2 负载力矩时间序列的回归分析
本文负载力矩时间序列m(t)的回归模型定义为:
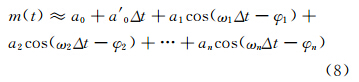
式中,a0为偏差;a′0为变化趋势项;ωn为不同周期变化的角频率;an和φn为相应周期变化的振幅和相位;Δt=ti-t0,本文中t0=2 000.0。
根据式(8),计算得到三个方向负载力矩时间序列的周年项振幅和相位,并将本文估计结果和Blewitt的实验结果分别列于表 1。
| 负载力矩 | mx | my | mz | |||
| 振幅/1022 kg·m | 相位/(°) | 振幅/1022 kg·m | 相位/(°) | 振幅/1022 kg·m | 相位/(°) | |
| 本文实验结果 (2000.0~2010.0) | 3.0±0.2 | 37±3 | 0.6±0.2 | 336±2 | 3.7±0.2 | 60±2 |
| Blewitt实验结果 (1995.642~ 2001.046) | 2.0±0.2 | 86±3 | 2.9±0.2 | 345±3 | 6.6±0.1 | 56±1 |
根据负载力矩各方向的周年相位,我们可以大致推断出负载力矩每年在地表的运动轨迹(图 4)。分析表 1中mz方向的相位可知,北半球地表负载力矩的最大值出现在每年的2、3月份,而南半球出现在8、9月份;结合表 1和图 4可知,地表负载力矩的最小值分别于5月和11月出现在古巴和印度尼西亚附近;每年的6~11月地表负载力矩主要集中在南半球,而12~5月主要集中在北半球,其中12月份出现在中国境内,这个时候地表负载力矩对中国范围的影响相对来说最为明显;此外,无论南北极点,其地表负载力矩最大值均出现在各自的冬季,中国也是如此。
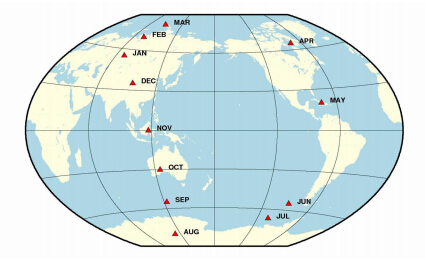 |
| 图 4 每年负载力矩在地球表面的运动轨迹Fig. 4 Annual Trajectory of the Load Moment on the Earth Surface |
为了更加深入研究地表负载力矩对中国范围 内测站的影响,选择09年12月的地表负载力矩时间序列,利用式(7)反算中国境内6个IGS站(BJFS、SHAO、WUHN、LHAZ、URUM、KUNM)的位移,结果列于表 2。
| 位移 | BJFS | SHAO | WUHN | LHAZ | URUM | KUNM |
| √ B2+ΔL2Δ | 0.281 1 | 0.179 1 | 0.172 7 | 0.181 7 | 0.275 8 | 0.180 6 |
| 0.354 1 | 0.193 1 | 0.179 5 | 0.181 4 | 0.336 2 | 0.188 3 | |
| 0.352 6 | 0.261 5 | 0.199 6 | 0.234 3 | 0.374 8 | 0.164 5 | |
| 0.400 7 | 0.236 6 | 0.193 3 | 0.201 3 | 0.395 6 | 0.205 0 | |
| ΔH | -0.469 5 | -0.573 4 | -0.605 6 | -0.307 6 | -0.521 8 | -0.636 9 |
| -0.370 3 | -0.511 5 | -0.593 1 | -0.390 9 | -0.510 6 | -0.614 4 | |
| -0.381 6 | -0.638 9 | -0.621 8 | -0.414 4 | -0.493 1 | -0.771 6 | |
| -0.557 2 | -0.372 7 | -0.661 4 | -0.324 8 | -0.420 8 | -0.403 0 | |
| 注:因为本文负载力矩时间序列是由周解反演得到的,故由负载力矩反算得到的测站位移均有4部分,其位移和即为整月IGS站的位移。 | ||||||
由表 2可知,由于地表负载力矩的作用,中国范围内的IGS站在12月份会下降2 mm左右,同 时伴有1 mm左右的水平位移。 4.4 分析与讨论
与Blewitt实验结果相比,本文估计的mx方向相位比Blewitt的结果要小,振幅与Blewitt的结果基本一致; my和mz方向相位与Blewitt的结果符合较好,振幅均比Blewitt的结果小得多。
分析认为,造成与Blewitt结果振幅相差较大的原因是Blewitt反演的数据源时间跨度为1995.642~ 2001.046,要早于本文数据源2000.0~2010.0,且时间跨度较短;本文所选用的测站坐标统一归算到ITRF05框架,其数据处理所采用模型的精度及接收机质量较Blewitt所使用的ITRF97框架的站点均有显著提高;此外,Blewitt选取的站点是3个IGS分析中心的66个GPS跟踪站(图 5),而本文选取的站点是IGS05框架的132个框架点(图 1),测站分布更广,更均匀,尤其在海洋上也有一定的观测资料,较之Blewitt的数据源更加稳定可靠。最后,Blewitt的模型中没有加入平移参数来削弱CN框架和CF框架之间的误差。
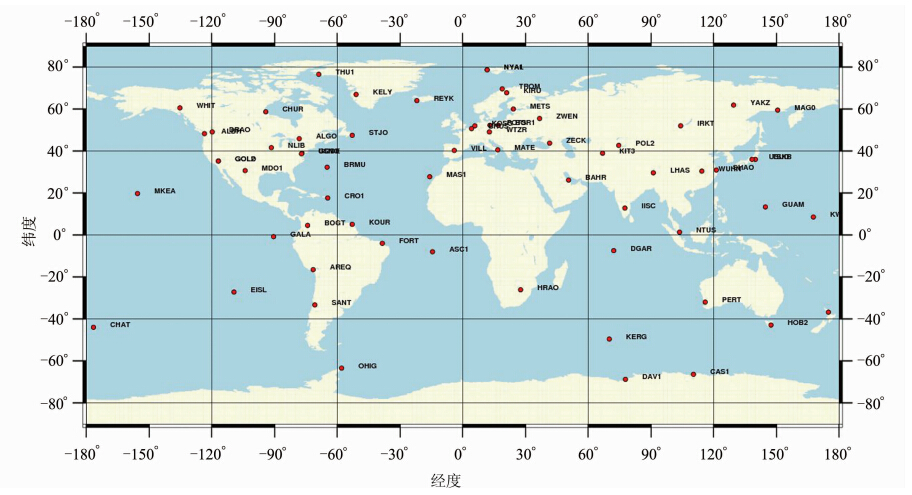 |
| 图 5 Blewitt实验数据源的测站分布Fig. 5 The Distribution of Blewitt’s Experimental Data Source |
本文利用IGS数据反演得到的季节性固体地球形变机制与已知的地球物理知识基本相符。研究结果显示,每年的2、3月份北半球地表负载最大,而8、9月份南半球地表负载最大;12月份地表负载力矩出现在中国境内,这将会造成中国范围的测站在水平和垂直方向分别产生1 mm和 2 mm左右的位移。因此,季节性固体地球形变对我国mm级CGCS2000框架的影响是不容忽视的。
地表液体层的质量再分布与地心运动密切相关,因此深入研究季节性固体地球形变对于季节性地心变化的研究具有十分重要的借鉴意义。
随着IGS服务的不断完善和发展,GPS对固体地球物理过程研究的意义越来越重大,然而GPS也有自身的缺陷,即IGS其跟踪站主要集中在陆地,占地球面积70%的海洋却缺少足够的观测资料;此外GPS跟踪站在陆地上的分布南北半球也不均匀,这会对单独使用GPS数据反演地表负载力矩的精度带来影响。如何将海洋数据和GPS数据融合来研究地表负载力矩,是下一步本文需要研究的内容。
| [1] | David A, Lavalle'e, Tonie van D, et al. Geocenter Motions from GPS:A Unified Observation Model[J]. Journal of Geophysical Research, 2006, 111:B05405 |
| [2] | Blewitt G. Self-consistency in Reference Frames, Geocenter Definition, and Surface Loading of the Solid Earth[J]. J. Geophys. Res., 2003, 108(B2):210-220 |
| [3] | Farrell W E. Deformation of the Earth by Surface Loads[J].Reviews of Geophysics and Space Physics, 1972, 10(3):761-797 |
| [4] | Diziewonski A, Anderson D L. Preliminary Reference Earth Model[J]. Phys. Earth Planet. Inter., 1981, 25:297-356 |
| [5] | Lambeck K. Geophysical Geodesy:The Slow Deformations of the Earth[M]. New York:Oxford Univ Press, 1988 |
| [6] | Blewitt G, Lavalle'D, Clarke P, et al. A New Global Mode of Earth Deformation:Seasonal Cycle Detected[J]. Science, 2001, 294(5 550):2 342-2 345 |
| [7] | Sun Fuping, Zhao Ming, Ning Jinsheng, et al. Detection of the Asymmetry of Global Tectonic Change Based on Space Geodetic Data[J].Chinese Science Bulletin, 1999, 44(20):2 225-2 229(孙付平, 赵铭, 宁津生, 等. 用空间大地测量数据检测地球的非对称性全球构造变化[J].科学通报, 1999, 44(20):2 225-2 229) |
| [8] | Sun Fuping, Zhu Xinhui, Wang Ren, et al. Detection of Changes of the Earth's Volume and Geometry by Using GPS and VLBI Data[J].Chinese Journal of Geophysic, 2006, 49(4):1 015-1 021(孙付平, 朱新慧, 王刃, 等. 用GPS和VLBI数据检测固体地球的体积和形状变化[J].地球物理学报, 2006, 49(4):1 015-1 021) |
| [9] | Shen Wenbin, Zhang Zhenguo. Detecting the Earth Expansion Effect Based on Space-geodetic Data[J]. Science of Surveying and Mapping, 2008, 33(3):5-6(申文斌, 张振国. 利用空间大地测量数据探测地球膨胀效应[J].测绘科学, 2008, 33(3):5-6) |
| [10] | Xia Yifei, Xiao Naiyuan, Ding Yuerong. The Deformation of the Elastic Earth and the Station Displacements[J]. Acta Astronomica Sinica, 1988, 29(3):278-286(夏一飞, 肖耐园, 丁月蓉. 弹性地球形变和台站位移[J].天文学报, 1988, 29(3):278-286) |
| [11] | Xu Jianqiao, Sun Heping. Earth's Deformation due to the Dynamical Perturbations of the Fluid Outer Core[J]. Acta Seismologica Sinica, 2002, 24(4):397-406(徐建桥, 孙和平. 液核动力学扰动引起的地球形变[J].地震学报, 2002, 24(4):397-406) |
| [12] | Song Shuli, Zhu Wenyao, Xiong Fuwen, et al. Construction of mm-level Terrestrial Reference Frame[J]. Chinese Journal of Geophysics, 2009, 52(11):2 704-2 711(宋淑丽, 朱文耀, 熊福文, 等. 毫米级地球参考框架的构建[J].地球物理学报, 2009, 52(11):2 704-2 711) |
| [13] | Dong D, Dickey J O, Chao Y, et al.Geocenter Variations Caused by Atmosphere, Ocean, and Surface Ground Water[J].Geophys. Res.Lett., 1997, 24:1 867-1 870 |
| [14] | Davies P, Blewitt G. Methodology for Global Geodetic Time Series Estimation:A New Tool for Geodynamics[J].J. Geophys. Res., 2000, 105(B5):11 083-11 100 |
| [15] | Jan K. A Guide to Using International GNSS Service(IGS) Products, Geodetic Survey Division, Natural Resources Canada[OL].ftp://igscb.jpl.nasa.gov/components/IGSProducts_user_v17.pdf, 2009 |
| [16] | Steigenberger P, Romero I, Fang P. Reprocessing Issues, Standardization, New Models[C]. IGS Workshop 2006, Darmstadt, Germany, 2006 |
 2015, Vol. 40
2015, Vol. 40


