文章信息
- 杜玉军, 王甫红, 王泽民, 刘万科
- DU Yujun, WANG Fuhong, WANG Zemin, LIU Wanke
- 导航卫星自主定轨星座旋转误差的地面校正算法
- A Correction Algorithm of Constellation Rotation Error in Autonomous Navigation Using Ground Stations
- 武汉大学学报·信息科学版, 2015, 40(4): 534-539
- Geomatics and Information Science of Wuhan University, 2015, 40(4): 534-539
- http://dx.doi.org/10.13203/j.whugis20140506
-
文章历史
- 收稿日期:2014-07-09
2. 武汉大学中国南极测绘研究中心, 湖北 武汉, 430079
2. Chinese Antarctic Center of Surveying and Mapping, Wuhan University, Wuhan 430079, China
卫星导航定位中所使用的导航电文通常是由地面监控系统生成和上传的,在战争中,如果地面监控系统全部被摧毁,卫星导航系统将很快陷入瘫痪。虽然卫星上存储有长期的广播星历,但星历的精度随着预报时间迅速下降,将会导致用户无法准确定位。为此,GPS组建初始,美国就开始研究自主定轨技术(或称自主导航)[1, 2],即导航卫星通过星间测距和数据交换,对星上存储的长期预报星历进行自动更新,使导航系统具备自主运行和服务能力,从而提高导航系统的战时生存能力。
然而在自主定轨中,地球定向参数EOP(Earth Orientation Parameters)的预报误差和星座整体在空间的任何进动均无法通过星间测距得到修正,这会造成自主定轨中出现系统性的旋转误差,严重影响用户导航定位的精度[1]。星座旋转问题本质上是由于缺少与地面相关的基准造成的,因而可以通过引入外部基准解决,如采用星地联合定轨[3]、增设地面锚固站[4]等方法。采用这一类方法可以解决星座旋转问题,但要求地面设备不断与卫星通信,降低了系统的自主性,且战时容易暴露目标。另外有学者提出通过校正的方法消除星座旋转的影响,如利用精度较高的短期预报EOP对卫星坐标或定位结果进行修正[5],或根据单点定位的误差来消除ΔΩ的影响[6]。这类方法简单有效,但前者依赖于其他EOP观测手段或数据源,在战时将受到极大限制;而后者由于仅考虑了ΔΩ的影响,不够完善,且校正结果容易受到观测条件和数据质量的影响。
本文提出一种基于区域常规地面站双频伪距观测值的星座旋转误差校正的滤波算法,该算法可以有效地校正星座旋转误差,简单易行,且在使用时具有较好的隐蔽性和独立性。通过星间仿真数据结合星地实测数据的分析,验证了该方法的可行性。 1 星座旋转误差的来源分析
在自主定轨中,如果只考虑星间相对观测,不可避免地会出现秩亏问题,使得星座的整体“漂移”不可观测,而这一现象集中体现在在轨道升交点赤经Ω上[7]。由于Ω比较容易进行长期预报[8],因而可以通过对其预报值进行合理约束,来解决秩亏的问题。卫星的各个轨道参数中,除了Ω外,其他参数的误差均可以通过星间测距得到修正。而如表每颗卫星的Ω预报值中均含有同一偏差ΔΩ时,并不影响星间测距值,因而无法得到修正。这部分误差便取决于Ω的预报精度,在自主定轨中表现为导航星座绕地球自转轴(Z轴)整体旋转ΔΩ角[6, 7]。表 1给出了GPS星座60 d的Ω预报精度(RMS值)及在赤道处对应的轨道误差。预报轨道以2012年2月1日0时的IGS精密星历为初值,通过轨道积分得到,顾及以下摄动力模型:地球引力采用EGM2008 12*12阶重力场模型,日月引力根据DE406星表计算日月位置,固体潮采用简易模型,太阳光压采用ECOM模型。从表 1可以看出,Ω预报误差随着时间逐渐积累,到第60 d时达到50 mas左右,相对应的轨道误差约为6 m。对于60 d的长期预报,Ω的精度已经很高,但仍会对自主定轨造成一定的影响。
| 积分天数 | Ω预报精度 /mas | 轨道误差 /m |
| 1 | 0.98 | 0.1 |
| 5 | 2.46 | 0.3 |
| 10 | 5.08 | 0.7 |
| 20 | 15.82 | 2.0 |
| 40 | 34.64 | 4.5 |
| 60 | 49.93 | 6.4 |
另外,自主定轨所生成的星历要经过从天球参考系CRS(Celestial Reference System,惯性系)到地球参考系TRS(Terrestrial Reference System,地固系)的转换,其转换关系通过一组EOP参数来描述,主要包括岁差和章动参数、极移参数以及UT1-UTC参数等。惯性系到地固系的转换关系为:
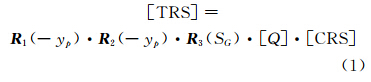
式中,[TRS]和[CRS]分别为卫星在地固系和惯性系下的坐标;R1、R2、R3分别代表关于X、Y、Z轴的旋转矩阵;xp、yp为极移参数;SG为格林尼治真恒星时角,是UT1-UTC的函数;[Q]为岁差-章动矩阵。
其中,岁差和章动参数有比较精确的长期预报模型,例如 IAU2000A模型的长期预报精度可达0.2 mas[9],模型预报误差对GPS轨道只有0.03 m左右的影响,在自主定轨中可以不予考虑;对于极移和UT1-UTC参数,由于受多种激发源的影响,变化极为复杂,很难长期准确地预报。表 2给出了IERS Annual Report 2012中EOP预报误差的RMS[10]以及可能对GPS造成的轨道误差。从表 2中可以看出,EOP参数的预报误差随时间逐渐增大,在预报90 d时,两个极移参数的误差分别达到22.1 mas和24.4 mas,可对GPS卫星造成3 m左右的轨道误差;而UT1-UTC的预报误差可达10.8 ms,这将引起赤道处的GPS轨道21 m左右的误差。
| 预报天数 | xp /mas | 轨道误差 /m | yp /mas | 轨道误差 /m | UT1-UTC /ms | 轨道误差 /m |
| 1 | 0.35 | 0.05 | 0.25 | 0.03 | 0.063 | 0.1 |
| 5 | 2.01 | 0.3 | 1.35 | 0.2 | 0.256 | 0.5 |
| 10 | 3.92 | 0.5 | 2.76 | 0.4 | 0.662 | 1.3 |
| 20 | 7.52 | 1.0 | 5.66 | 0.7 | 2.22 | 4.3 |
| 40 | 13.7 | 1.8 | 11.3 | 1.5 | 5.77 | 11.1 |
| 90 | 22.1 | 2.8 | 24.4 | 3.1 | 10.8 | 20.9 |
当导航系统进入自主定轨模式后,地面至卫星的上行通信链路中断,卫星无法对EOP参数进行更新,只能使用长期预报EOP。随着预报时间的增长,EOP精度逐渐下降,必然导致自主定轨精度的下降。由式(1)可知,EOP的预报误差将反映在三个旋转矩阵中,因而不可避免地导致星座旋转误差。从表 2中还可以看出,UT1-UTC所引起的轨道误差较极移参数大一个数量级,是主要误差源。根据式(1),UT1-UTC的误差同样 也会引起星座绕地球自转轴(Z轴)的整体旋转。
综合可知,引起星座旋转的主要误差源是轨道升交点赤经的系统偏差ΔΩ和EOP参数的预报误差;星座整体旋转主要体现在关于地球自转轴(Z轴)的旋转,由ΔΩ和EOP中UT1-UTC参数的预报误差共同引起,两者无法区分;极移参数的预报误差会引起星座关于X、Y轴的旋转,但量级相对较小。 2 星座旋转误差滤波校正算法
2.1 观测方程和状态方程
在某一时刻,卫星i到测站j之间的伪距观测方程为:

式中,ρij为伪距观测值;XiS和XR,j分别为卫星i和测站j的三维坐标向量;dTR,j和dTiS分别为接收机和卫星钟差;dIonoji和dTropji分别为电离层和对流层延迟;c为光速;εij为观测噪声。
当存在星座旋转时,根据导航电文计算的卫星坐标(记为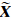 iS)并不是真实坐标,而需要进行一个旋转变换,即:
iS)并不是真实坐标,而需要进行一个旋转变换,即:
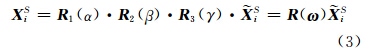
式中,ω =(α,β,γ)为旋转误差的三维矢量,由前面的分析可知α和β对应于xp、yp的预报误差,而γ对应于(ΔΩ+ΔSG)。这时观测方程应为:
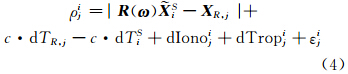
以ω为待估量,顾及接收机钟差,可以利用最小二乘方法求解。在本文中,对于观测方程中的各项误差,对流层延迟采用Saastamoinen模型进行改正;考虑到实时性和改正效果,电离层延迟采用双频模型进行改正;卫星钟差仍使用广播星历中的二项式钟差模型。
受卫星数量、几何分布以及观测质量等影响,单历元旋转估值中会有噪声。由于Ω和EOP预报误差随时间的变化较为平缓,不会出现高频振荡,可以将在短时间内的变化视为随机误差,采用随机游走模型进行卡尔曼滤波估计,其状态方程为:

式中,X=[α β γ dTR,j]为待估状态; w 为过程噪声;Φ为状态转移矩阵,对于随机游走模型来说,Φ = I为单位阵。
EOP预报误差和ΔΩ在短时间内变化很小,对于本文的算例,两者每天的变化不超过3 mas,因而在一天之内可以近似地将ω视为常数,每天观测一组参数即可。在实际使用时,可采取两种方案:① 每天进行一次旋转参数的滤波更新,并通过网络、广播等方式发布给用户进行改正;② 用户提前自行测定旋转参数,在接下来的一天之内用这组参数进行校正,测定旋转参数时需要对每个历元进行滤波更新,直到收敛为止。用户在定位时,需首先按照式(3)中的关系对自主定轨的星历进行校正。 2.2 地面站的数量要求论证
根据旋转矩阵的正交性,即R(ω)·R(ω)T= I ,观测方程(4)还可以表示为:

这说明,如果不对星座进行校正,旋转误差将反映在定位结果中。设这个坐标矢量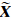 R=R(ω)TXR,j,则有:
R=R(ω)TXR,j,则有:
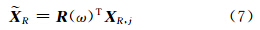
对于ω为小角度的情况,不难推出:

式(8)矩阵秩亏(秩亏数为1),说明当式(7)中只有一组方程时,即仅用一个测站是无法求解三维旋转参数的,至少需要两个测站。
由§1讨论可知,星座关于X、Y轴的旋转分量α、β相对较小,因而可以忽略这两个参数,只估计γ,这样只用一个测站也可以消除大部分旋转误差;如果条件允许,可以同时使用两个地面站进行观测,求解三个旋转分量,实现较完善的校正。 3 仿真验证及结果分析
本文以GPS为例进行了自主定轨的仿真。仿真时间为2010-6-10~2012-8-8,约化儒略日(MJD)为55358~55416,选取未发生轨道机动和时钟调整的25颗卫星组成仿真星座,根据文献[11]中的算法,按照TDMA(时分多址)制式仿真生成星间观测数据,并利用自主研制的软件进行自主定轨。星间测距的间隔为5 min,测量噪声为0.3 m(1 σ)。自主定轨考虑的动力学模型与§1中轨道积分所采用的模型相同。自主定轨中EOP参数采用IERS发布的Bulletin A预报产品。地面站观测数据选取了北京(BJFS)和上海IGS跟踪站(SHAO)的双频伪距实测数据,采样间隔为30 s。
分别采用§2.1中的两种校正方案进行星座旋转的校正处理。方案一:分别选用一个站(BJFS)和两个站(BJFS+SHAO),仅在每日零时进行旋转参数的滤波更新,用户采用最近一次的滤波结果进行旋转校正。当采用一个站时,只估计关于Z轴的旋转分量,而当采用两个站时,估计三维旋转参数。方案二:用户从某一时刻开始对各历元进行连续的滤波处理,收敛后在不超过1 d的时间内使用这一组参数进行旋转校正。考虑到实用性,方案二只讨论一个站的情况。
3.1 方案一
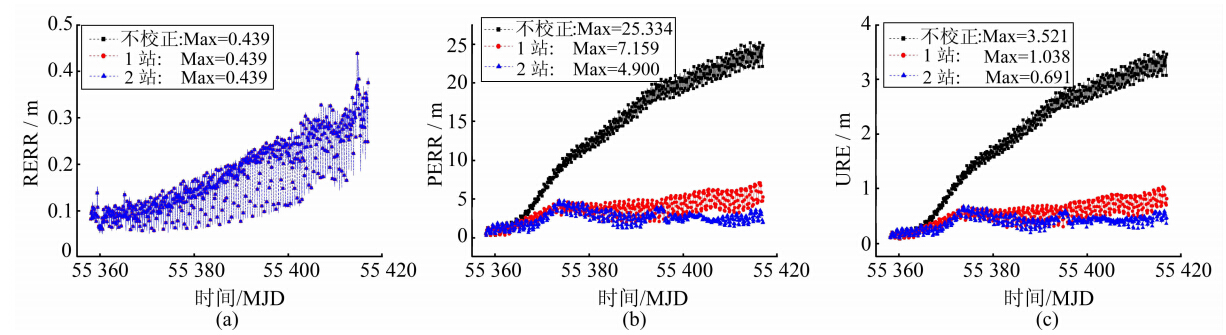
以IGS精密星历作为真值,根据文献[1]中的方法 统计旋转误差校正前后星座的径向误差RERR、平面误差PERR(切向和法向综合误差)和用户测距误差URE(user range error),指轨道误差和卫星钟差投影到用户测距方向的综合误差,用于评定轨道精度,结果如 图 1所示。可以看到,如果不进行旋转校正,自主定轨的精度随时间逐渐下降,在60 d内全星座平面误差PERR可以达到25 m以上,URE可达3.5 m;由于星座旋转只会造成卫星轨道在切向和法向上的误差,而不会对径向产生影响,径向误差RERR在60 d内不超过0.5 m,相对于星座旋转的误差,可以忽略不计。
 |
| 图 1 自主定轨星座旋转校正前后轨道精度统计Fig. 1 Autonomous Navigation Accuracy Achievable With and Without Rotation Correction |
利用区域地面站的伪距观测值对星座旋转进行校正,采用一个地面站时,仅考虑星座绕Z轴的旋转,即可大幅度地提高轨道的精度,星座的PERR减小到7.2 m以下,URE在1.1 m以内,说明采用本文方法可以有效地消除自主定轨的星座旋转误差;采用两个地面站时,可以同时估计旋转的三个分量,因而相比采用一个地面站时校正效果更优,星座的PERR和URE分别减小到5 m和0.7 m以下;而对于RERR,是否进行旋转校正,没有任何影响。 3.2 方案二
对于方案二,本质上与方案一采用一个地面站的情况相同,区别仅在于要事先进行多个历元的观测,并且需要一定的收敛时间。图 2给出了自主定轨第60 d(2012-8-8)旋转参数滤波估值的时间序列,滤波起始时刻为零时,初值为0。为了便于比较,用黑色实线标出了方案一使用一个测站的旋转估值,虚线标出了收敛时间。可以看出,采用该方案估计星座旋转参数,以0为初 值,经过大约20 min即可以收敛。选择收敛后(如第25 min)的估值对自主定轨的星历进行较正,统计当天校前正后的平均PERR、RERR和URE,并与方案一同一天的结果进行比较,结果如表 3所示。
 |
| 图 2 方案二旋转参数滤波估值的时间序列Fig. 2 Time Series of Rotation Estimation Achievable with Case 2 |
| 校正方案 | RERR | PERR | URE |
| 自主定轨(不校正) | 0.310 | 23.652 | 3.292 |
| 方案一(1个站) | 0.310 | 5.947 | 0.883 |
| 方案二(1个站) | 0.310 | 6.317 | 0.931 |
从表 3中可以看到,采用方案二对星座旋转进行校正,也可以有效消除星座旋转误差。对第60 d的自主定轨星历进行校正后,平均PERR为6.317 m,URE为0.931 m,相对于校正前的23.652 m和3.292 m,精度提高了将近3倍;两种校正方案的校正效果差异很小。由此可见,用户可以使用一台接收机独立、有效完成自主定轨星座旋转的校正,说明此种方法较为实用,尤其在战时等特殊情况下,将具有很强的应用价值。
3.3 单点定位验证
为了进一步验证校正算法对用户导航定位的影响,采用自主定轨第60 d武汉IGS站(WUHN)的实测数据,分别采用IGS精密星历、自主定轨星历以及通过不同方案校正后的星历进行伪距单点定位,并将定位结果与测站的精确坐标进行比较,统计N、E、U三个方向的均值误差和标准差,结果如表 4所示。单点定位中电离层和对流层改正模型与§2.1中的描述一致。
| 方案 | 均值误差/m | 标准差/m | ||||
| N | E | U | N | E | U | |
| IGS精密星历 | 0.560 | -0.223 | 3.700 | 1.918 | 1.307 | 4.211 |
| 自主定轨(不校正) | 1.058 | 6.263 | 3.808 | 1.993 | 1.421 | 4.296 |
| 方案一(2个站) | 0.414 | -0.366 | 3.806 | 1.993 | 1.421 | 4.296 |
| 方案一(1个站) | 1.058 | -0.462 | 3.808 | 1.993 | 1.421 | 4.296 |
| 方案二(1个站) | 1.058 | -0.615 | 3.808 | 1.993 | 1.421 | 4.296 |
均值误差和标准差分别反映了定位结果的系统误差和随机误差。可以看到,对于本算例中不同星历定位的结果,U方向的精度是基本一致的,这主要是由于星座旋转并不对高程方向造成影响;同时,各方向的标准差也几乎相同,说明星座旋转主要对定位结果造成系统误差;利用未经校正的自主定轨星历进行单点定位,在N、E两方向上分别存在1.058 m和6.263 m的均值误差,与用IGS精密星历定位的结果相比存在明显的系统性偏差,在E方向上尤为显著,这也反映了星座旋转主要是绕地球自转轴的旋转,验证了本文前面的分析。利用本文提出的算法,使用两个测站校正星座旋转,对N、E方向的定位精度都有提高,校正后的定位精度与IGS精密星历参与定位的精度相当;而使用一个测站校正星座旋转,只对E方向有明显改进,较使用两个测站的方案略差;方案二与方案一使用一个测站的改正效果相当。 4 结 语
本文对自主定轨星座旋转误差的来源进行了分析,在此基础上提出一种利用区域地面站的伪距观测值校正星座整体旋转误差的算法,通过仿真实验,得出如下结论。
1)导航卫星进行长时间自主定轨时,星座旋转误差随时间不断积累,造成轨道切向和法向的误差,进而使用户定位在平面方向产生系统性偏差;轨道升交点赤经的系统偏差ΔΩ和EOP预报误差是星座旋转的主要误差源,主要引起星座绕地球自转轴(Z轴)的旋转,因而在定位中对E方向的影响更为显著;
2)根据本文算法,利用少数区域地面站的伪距观测值可以估计并校正自主定轨的星座旋转误差,但至少需要两个测站才能估计旋转的三个分量;
3)采用两个测站可以较为完善地校正星座旋转,对于本文算例,星座的PERR误差由25 m以上减小到5 m以下,URE由3.5 m提高到0.7 m以内;用校正后的星历进行伪距单点定位可以达到与用IGS精密星历定位相当的精度;
4)如果仅估计绕Z轴的旋转分量,采用一个测站即可以校正大部分旋转误差,校正后星座的PERR误差优于7.2 m,URE在1.1 m以内;使用一个测站校正星座旋转,只能改善E方向的定位精度,校正效果略差,但用户使用一个接收机就可以完成旋转的校正,有更强的实用性。
| [1] | Ananda M P, Bernstein H, Cunningham K E, et al. Global Positioning System (GPS) Autonomous Navigation [C]. IEEE Position Location and Navigation Symposium, Las Vegas, NV, 1990 |
| [2] | Rajan J A. Highlights of GPS II-R Autonomous Navigation [C]. ION 58th Annual Meeting/CIGTF 21st Guidance Test Symposium, Albuquerque, NM, 2002 |
| [3] | Liu Wanke, Gong Xiaoying, Li Zhenghang, et al. Combined Orbit Determination of Navigation Satellites with Cross-link Ranging Observations and Ground Tracking Observations [J].Geomatics and Information Science of Wuhan University, 2010, 35(7):811-815 (刘万科, 龚晓颖, 李征航, 等. 综合星间和地面测距数据的导航卫星联合定轨[J]. 武汉大学学报·信息科学版, 2010, 35(7):811-815) |
| [4] | Rajan J A, Brodie P, Rawicz H. Modernizing GPS Autonomous Navigation with Anchor Capability[C]. ION GPS/GNSS 2003, Portland, OR, 2003 |
| [5] | Li Zhenghang, Gong Xiaoying, Liu Wanke, et al. Correction of Earth Orientation Parameter Error in AOD of Navigation Satellite[J]. Journal of Geodesy and Geodynamics, 2012, 32(6):71-75 (李征航, 龚晓颖, 刘万科, 等. 导航卫星自主定轨中地球定向参数误差的修正[J]. 大地测量与地球动力学, 2012, 32(6):71-75) |
| [6] | Li Zhenghang, Lu Zhenzhu, Liu Wanke, et al. Method for Eliminating Systematic Error ΔΩ and Δt in Autonomous Orbit Determination of Navigation Satellites [J]. Geomatics and Information Science of Wuhan University, 2007, 32(1):27-30 (李征航, 卢珍珠, 刘万科, 等. 导航卫星自主定轨中系统误差ΔΩ和Δt的消除方法[J]. 武汉大学学报·信息科学版, 2007, 32(1):27-30) |
| [7] | Liu Lin, Liu Yingchun. Rank Deficiency About Crosslink Relative Measurement in Autonomous Navigation [J]. Journal of Spacecraft TT&C Technology, 2000, 29(3):13-16 (刘林, 刘迎春. 关于星–星相对测量自主定轨中的亏秩问题[J]. 飞行器测控学报, 2000, 29(3):13-16) |
| [8] | Chen Jinping, Jiao Wenhai, Ma Jun, et al. Autonav of Navigation Satellite Constellation Based on Crosslink Range and Orientation Parameters Constraining [J]. Geomatics and Information Science of Wuhan University, 2005, 30(5):439-443(陈金平, 焦文海, 马骏, 等. 基于星间测距/轨道定向参数约束的导航卫星自主定轨研究[J]. 武汉大学学报·信息科学版, 2005, 30(5):439-443) |
| [9] | McCarthy D D, Petit G. IERS Conventions (2003) [OL]. http://www.iers.org/ERS/EN/Publications/TechnicalNotes, 2004 |
| [10] | Wolfgang R D, Daniela T. International Earth Rotation and Reference Systems Service (IERS) [OL]. http://www.iers.org/IERS/EN/Publications/AnnualReports, 2014 |
| [11] | Wang Fuhong, Liu Wanke, Lin Xiaojing. Distributed Autonomous Orbit Determination of Global Navigation Constellation via Inter-Satellite Pseudo-Ranging Measurements [C].The 2nd China Satellite Navigation Conference(CSNC2011), Shanghai, 2011(王甫红, 刘万科, 林晓静. 分布式导航卫星自主定轨滤波算法与模拟分析[C]. 第二届中国卫星导航学术年会(CSNC2011), 上海, 2011) |
 2015, Vol. 40
2015, Vol. 40



