文章信息
- 唐卫明, 徐坤, 金蕾, 文雪中
- TANG Weiming, XU Kun, JIN Lei, WEN Xuezhong
- 北斗/GPS组合伪距单点定位性能测试和分析
- Test and Analysis of BeiDou/GPS Combined Pseudo-range Point Positioning Performance
- 武汉大学学报·信息科学版, 2015, 40(4): 529-533
- Geomatics and Information Science of Wuhan University, 2015, 40(4): 529-533
- http://dx.doi.org/10.13203/j.whugis20130361
-
文章历史
- 收稿日期:2013-07-26
2. 重庆市勘测院, 重庆, 400020
2. Chongqing Survey Institute, Chongqing 400020, China
GPS能为全球用户提供高精度的导航定位服务,但在观测条件较差时,其可见卫星数、定位精度和可用性都有所下降[1, 2]。北斗卫星导航系统(BDS)已正式向我国及周边地区提供区域服务,作为全球GNSS的重要组成部分,北斗与GPS的联合定位和导航也将是未来GNSS的重要发展方向[3]。
受限于北斗的建设过程,此前众多学者对其进行的研究多基于仿真系统,并不能完全反映系统真实性能[4, 5, 6]。随着北斗区域服务的正式开放,利用北斗和GPS组合定位也进入了利用实测数据分析论证的新阶段。本文利用北京、武汉测站的BDS/GPS双系统观测数据,研究BDS/GPS组合伪距单点定位对单一系统定位精度和可用性等的改善情况。 1 BDS/GPS伪距单点定位联合解算 1.1 时间基准与坐标基准
BDS与GPS是两个独立的导航系统,它们的时间系统不同步,确定卫星轨道的坐标框架也不同。北斗时(BDT)与GPS时(GPST)均采用原子时时间基准。BDT起始历元为2006年1月1日协调世界时(UTC)0时0分0秒,GPST起始历元为1980年1月6日UTC 0时0分0秒,由于UTC闰秒,BDT与GPST之间在周秒部分总有14 s的差异。又由于BDT与GPST二者原子时的维持存在差异,故BDT与GPST除了周秒相差14 s以外,还存在微小的同步误差。BDS广播星历坐标系采用CGCS2000,GPS广播星历坐标系为WGS84,二者定义一致,但框架实现有差异[7, 8]。在坐标系的实现精度范围内,CGCS2000和WGS84坐标一致,在cm级精度的数据处理过程中,无需考虑坐标系差异引起的结果偏差[9]。
本文研究对象为伪距单点定位,其精度受限于广播星历和伪距观测的精度而较低,故在数据处理过程中,忽略了BDT与GPST之间除了整秒以外的微小同步误差,也不考虑坐标系不同引起的结果偏差。
1.2 数学模型
GPS和BDS伪距单点定位的观测方程分别为:
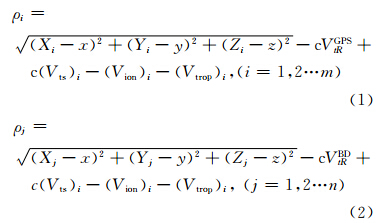
式中,下标i、j分别表示GPS、BDS卫星序号;(x,y,z)为测站坐标;(Xi,Yi,Zi)和(Xj,Yj,Zj) 分别表示GPS和BDS卫星坐标;VtRGPS 和VtRBD分别表示GPS和BDS的接收机钟差;Vts、Vion、Vtrop 分别表示卫星钟差、电离层延迟和对流层延迟;ρ 表示伪距;c表示真空中光速[8]。
将观测方程(1)、(2)在测站近似坐标(x0,y0,z0)处用泰勒级数展开,得到误差方程:
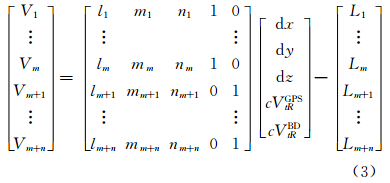
式中,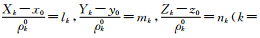 nk
(k=1,2,…,m+n) 为从测站近似位置至卫星k方向的方向余弦;ρ0k为信号发射时刻第k颗卫星至测站近似位置的几何距离;dx、dy、dz为测站坐标的改正数;常数项为:
nk
(k=1,2,…,m+n) 为从测站近似位置至卫星k方向的方向余弦;ρ0k为信号发射时刻第k颗卫星至测站近似位置的几何距离;dx、dy、dz为测站坐标的改正数;常数项为:
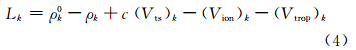
设式(3)系数矩阵为B,待估未知数矩阵为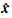 ,常数阵为L ,观测值权阵为P,由最小二乘估计可得:
,常数阵为L ,观测值权阵为P,由最小二乘估计可得:
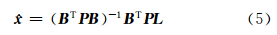
待估参数中含3个坐标差参数和两个接收机钟差参数,理论上至少需要观测两个系统的至少5颗卫星才能求解。
本文仅使用BDS的B1和GPS的L1频率进行单频伪距定位,电离层延迟改正使用CODE的球谐函数模型[8],对流层延迟改正使用简化的Hopfield模型[10],观测值定权方式采用简单的卫星高度角定权。且为了更方便地分析BDS、GPS、BDS/GPS三种模式定位差异,将BDS与GPS观测值视为等权,即不再根据卫星系统进一步定权。 2 实测数据测试分析
本文数据来源于北斗跟踪站实验网中的北京站(BJF1)和武汉站(CENT),数据包含2013年1月23日全天采样间隔为1 s的BDS和GPS双系统观测数据。根据卫星方位角剔除部分观测卫星,模拟多种遮挡环境。按方位角剔除观测卫星条件如下:
1) 无遮挡:不剔除卫星。
2) 半边天空遮挡。 ① 东:剔除方位角为0°~180°的卫星; ② 南:剔除方位角为90°~270°的卫星; ③ 西:剔除方位角为180°~360°的卫星; ④ 北:剔除方位角为0°~90°和270°~360°的卫星。
3) 城市街道/峡谷。 ① 东西向:剔除方位角为0°~45°、135°~225°、315°~360°的卫星; ② 南北向:剔除方位角为45°~135°、225°~315°的卫星。 2.1 可 见卫星数和PDOP值
当观测卫星数目较多时,空间较好的卫星几何分布可使位置精度因子(PDOP)值较小,定位精度提高[11]。根据程序计算结果,BDS、GPS、BDS/GPS三种定位模式在各环境类型下的可见卫星数在1 d内的平均值如表 1所示。
| 站点 | 模式 | 无遮挡 | 半边天遮挡 | 街道/峡谷 | ||||
| 东 | 南 | 西 | 北 | 东西 | 南北 | |||
| 北京 | BDS | 9.57 | 5.96 | 1.66 | 3.60 | 7.91 | 4.59 | 4.98 |
| GPS | 8.54 | 4.04 | 4.70 | 4.50 | 3.84 | 5.60 | 2.94 | |
| B/G | 18.1 | 10.0 | 6.36 | 8.11 | 11.8 | 10.2 | 7.93 | |
|
武 汉 | BDS | 9.92 | 6.06 | 2.05 | 3.86 | 7.87 | 4.45 | 5.48 |
| GPS | 8.64 | 4.14 | 4.84 | 4.50 | 3.80 | 4.51 | 4.12 | |
| B/G | 18.6 | 10.2 | 6.88 | 8.36 | 11.7 | 8.96 | 9.60 | |
| 注:B/G为BDS/GPS的缩写,表示BDS/GPS组合系统,下文同。 | ||||||||
表 1中,在无遮挡环境下,北京、武汉两站组合系统平均可见卫星数均超过了18颗,且BDS平均每个历元比GPS多观测1颗卫星。遮挡半边天环境下,GPS可见卫星数较无遮挡时近似减半,在4个方向遮挡的平均值均为4颗左右;组合系统在西、南面遮挡后可见卫星平均不到9颗,BDS在南面遮挡后平均值锐减至1~2颗;城市街道/峡谷中,BDS在两个走向中都能平均观测到5颗左右卫星,南北走向的平均值均比GPS大。
遮挡南面时BDS可见卫星数骤减至1~2颗,这是因为BDS采用了GEO和IGSO卫星对我国及周边地区实施了区域增强[7],其中5颗GEO卫星在赤道上空,无遮挡时在区域内长期可见。北京、武汉两测站地处北半球,当遮住测站南面半边天时,这5颗GEO卫星都不可见,此时BDS可见卫星数锐减,大部分时段甚至不能达到4颗星,无法完成定位。而GPS采用MEO卫星,在全球分布较为均匀,所以各方向遮挡时卫星数变化也较均匀。
由于组合系统的可见卫星较单一系统增多,组合系统的PDOP值较单一系统有所减小。表 2给出了各环境下两站观测卫星PDOP值在(1,3)和(1,10)区间分布的百分比。
| 范围 | 模式 | 无遮挡 | 半边天遮挡 | 街道/峡谷 | |||||
| 东 | 南 | 西 | 北 | 东西 | 南北 | ||||
| 北京 | <3 | BDS | 98.7 | 0 | 0 | 0 | 40.3 | 10.9 | 0 |
| GPS | 98.0 | 4.1 | 2.7 | 3.4 | 3.9 | 45.5 | 5.7 | ||
| B/G | 100 | 28.6 | 6.9 | 17.2 | 91.0 | 94.3 | 26.0 | ||
| <10 | BDS | 100 | 76.5 | 0 | 23.8 | 96.3 | 85.3 | 56.1 | |
| GPS | 100 | 50.4 | 68.7 | 65.6 | 50.9 | 93.7 | 26.0 | ||
| B/G | 100 | 100 | 81.2 | 92.8 | 100 | 100 | 94.1 | ||
| 武汉 | <3 | BDS | 99.6 | 0 | 0 | 0 | 44.5 | 2.7 | 2.3 |
| GPS | 96.7 | 6.8 | 4.8 | 1.8 | 1.3 | 20.2 | 23.0 | ||
| B/G | 100 | 32.8 | 13.9 | 18.6 | 91.6 | 76.2 | 64.2 | ||
| <10 | BDS | 100 | 84.0 | 1.2 | 25.7 | 98.4 | 79.2 | 69.6 | |
| GPS | 100 | 56.0 | 80.4 | 62.2 | 46.1 | 73.4 | 53.4 | ||
| B/G | 100 | 100 | 88.6 | 90.4 | 100 | 100 | 99.8 | ||
表 2显示,无论在何种环境条件下,组合系统PDOP值在(1,3)区间的百分比都比BDS、GPS单系统要大,其中无遮挡环境下组合系统PDOP值小于3的比例达到了100%;组合系统PDOP值即使在东、北面遮挡以及东西向街道/峡谷环境下,小于10的比例也达到了100%,在西面遮挡和南北向街道/峡谷环境下小于10的比例超过了90%,在南面遮挡环境下小于10的比例超过了80%。 2.2 定位精度和可用性
本文在进行精度分析时,将各历元解算坐标与测站真值的偏差换算为站心直角坐标方向(N,E,U)后,重点对平面(H)和高程(U)方向的偏差进行分析,其中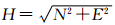 。三种定位模式在不同环境类型下的定位偏差如图 1所示(限于篇幅,仅给出北京站分析结果,武汉站结论一致)。
。三种定位模式在不同环境类型下的定位偏差如图 1所示(限于篇幅,仅给出北京站分析结果,武汉站结论一致)。
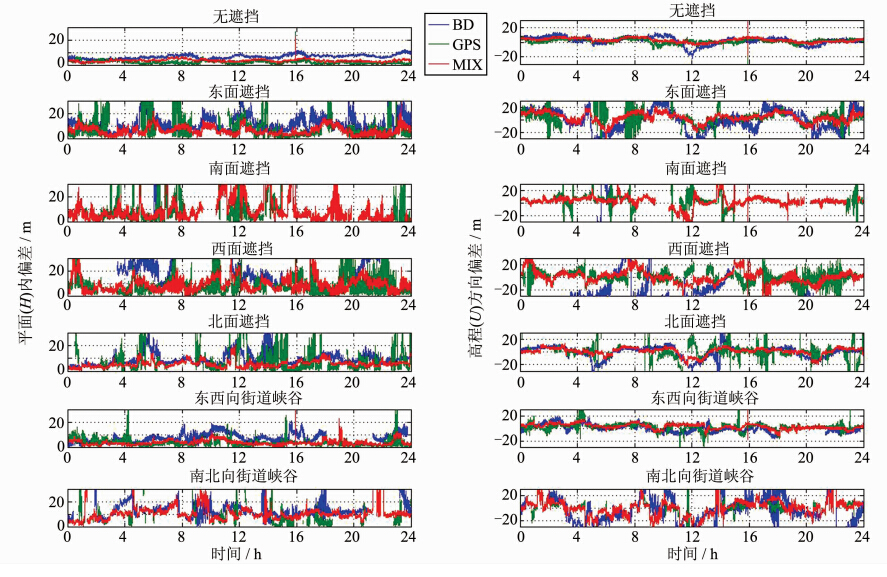 |
| 图 1 BJF1在平面(左)和高程(右)方向的定位偏差Fig. 1 Positioning Bias of BJF1 in Horizontal Plain (left) and Elevation (right) |
经计算,北京站在无遮挡环境下,BDS、GPS、BDS/GPS在 1 d内平面方向定位偏差的RMS值分别为6.71 m、2.40 m、3.59 m,在高程方向定位偏差的RMS值分别为5.72 m、3.18 m、3.84 m,结合图 1中第一行的两幅图也可知,GPS定位偏差最小,BDS/GPS次之,BDS最大。造成此现象的原因为:BDS测距精度和信号稳定性比GPS略差,且BDS内部不同种星座的测距精度和多路径效应也有差别;而在BDS/GPS联合解算时将BDS与GPS观测值视为等权,不精确的随机模型导致组合定位结果精度低于GPS[12]。
半边天遮挡环境下,图 1中BDS在东、北面遮挡后可定位历元都占总历元的100%,西面遮挡后可定位历元减至54.7%,南面遮挡后骤减至4.5%;GPS在4个方向的遮挡可定位历元都超过了60%;BDS/GPS仅南面遮挡后可定位历元为90%,其他方向都为100%。以BDS可见卫星数最少和最多的南面、北面遮挡为例,南面遮挡后GPS和BDS可定位历元在平面和高程方向偏差的RMS值都大于100 m,而组合系统在平面和高程方向分别为16.3 m和9.4 m;北面遮挡后,GPS在平面和高程偏差的RMS值仍大于100 m,而BDS则分别减小到13.3 m和11.3 m,组合系统分别减小到6.1 m和5.9 m。结合表 1,因为南、北面遮挡后GPS可见卫星减半至4颗左右,导致无法定位或定位结果很差,而北斗卫星在测站南面分布较多,北面遮挡对BDS定位影响较小。组合系统定位精度随着组合卫星数的增加而提高。
街道/峡谷环境下,图 1显示东西走向定位精度优于南北走向,结合表 2中东西向PDOP值在(1,3)和(1,10)的百分比普遍大于南北向可知,东西向可见卫星比南北向具有更好的几何分布。
表 3按照5个精度等级统计了北京站在不同环境下三种定位模式的三维导航可用性指标。本文中统计的导航可用性即为定位三维偏差在特定精度范围内的历元数占全部观测历元的百分比。
| 精度 /m | 模式 | 无遮挡 | 半边天遮挡 | 街道/峡谷 | ||||
| 东 | 南 | 西 | 北 | 东西 | 南北 | |||
| BDS | 2.9 | 1.48 | 0.01 | 0.03 | 1.6 | 1.8 | 0.3 | |
| ≤5 | GPS | 76.40 | 16.9 | 24.3 | 16.4 | 20.4 | 47.6 | 9.3 |
| B/G | 60.74 | 22.0 | 23.4 | 8.6 | 19.0 | 44.7 | 2.9 | |
| BDS | 80.04 | 22.8 | 0.5 | 2.0 | 51.1 | 51.0 | 6.3 | |
| ≤10 | GPS | 99.95 | 37.7 | 57.4 | 53.6 | 38.5 | 87.7 | 19.2 |
| B/G | 99.75 | 57.2 | 58.1 | 48.6 | 81.6 | 91.3 | 27.1 | |
| BDS | 99.93 | 64.2 | 1.2 | 7.1 | 87.5 | 85.2 | 45.7 | |
| ≤20 | GPS | 99.99 | 56.3 | 77.9 | 78.4 | 51.0 | 94.8 | 25.4 |
| B/G | 99.99 | 96.0 | 76.5 | 84.9 | 99.0 | 100 | 80.4 | |
| BDS | 100 | 98.6 | 1.8 | 34.0 | 99.1 | 85.3 | 80.0 | |
| ≤50 | GPS | 100 | 65.0 | 85.4 | 87.7 | 61.0 | 96.4 | 27.7 |
| B/G | 100 | 100 | 87.5 | 99.5 | 100 | 100 | 97.6 | |
| BDS | 100 | 100 | 2.5 | 50.9 | 99.6 | 85.3 | 86.0 | |
| ≤100 | GPS | 100 | 66.8 | 87.4 | 88.9 | 62.8 | 96.7 | 28.1 |
| B/G | 100 | 100 | 90.6 | 100 | 100 | 100 | 98.9 | |
首先从环境类型来分析。在无遮挡环境下,北京站10 m精度内的GPS、北斗/GPS可用性已经达到了99%以上,北斗在20 m精度内也已经达到99.9% 以上,且三种定位模式在50 m精度内的可用性都达到了100%。半边天遮挡时,西、南面遮挡后,北斗在100 m精度内可用性仅分别为50.9%和2.5%,而东、北面遮挡后可用性分别为100%和99.6%,表现出了极大的向异性;受北斗可见卫星数影响,组合系统在南面遮挡后100 m精度内的可用性仅为90.6%,其他三面的遮挡都为100%。街道/峡谷环境下,三种定位模式在东西走向的可用性普遍大于南北走向,主要是由于东西向可见卫星具有更好的几何分布。
从定位精度来分析,在5 m、10 m精度级别,北斗可用性均相对较小,且当GPS观测卫星数较多时,GPS可用性比组合系统稍大,当GPS观测卫星数较少时,GPS可用性比组合系统差;在50 m、100 m精度级别,观测卫星数差异导致的三种定位模式可用性有了较明显的差别,组合系统的可用性比北斗和GPS都有了显著提高,且除了较特殊的南面遮挡外,组合系统可用性都达到了97%以上,在100 m级别的可用性接近100%。 3 结 语
本文在多种模拟遮挡环境下将BDS/GPS联合解算结果与BDS、GPS单系统在可见卫星数、PDOP值、定位精度、可用性等方面进行了对比分析,初步结论如下:①BDS/GPS组合系统能大大增加单一系统的观测卫星数,改善卫星空间分布,能有效减小系统PDOP值。②当测站南面遮挡严重时,北斗卫星观测将受到很大影响,造成北斗系统无法定位或定位精度大大降低,在100 m导航精度内可用性不超过10%。③在遮挡环境下,导航精度级别内,BDS/GPS组合系统有效提高了单系统的导航可用性,在50m精度内历元可用性提升至97%以上(南面遮挡除外),南面遮挡时在100 m精度内历元可用性提升至90%以上,且有效地提高了定位精度。
| [1] | Pirti A. Accuracy Analysis of GPS Positioning near the Forest Environment[J]. Croatian Journal of Forest Engineering, 2008, 29(2):189-199 |
| [2] | Wang Zemin, Meng Yang, Wu Yue, et al. DOP for GPS, Galileo and Combination Navigation System[J]. Geomatics and Information Science of Wuhan University, 2006, 31(1):9-11(王泽民, 孟泱, 伍岳, 等. GPS、Galileo及其组合系统导航定位的DOP值分析[J]. 武汉大学学报·信息科学版, 2006, 31(1):9-11) |
| [3] | Yang Yuanxi. Progress, Contribution and Challenges of Compass/Beidou Satellite Navigation System[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1):1-6(杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报, 2010, 39(1):1-6) |
| [4] | Chen H C, Huang Y S, Chiang K W, et al. The Performance Comparison Between GPS and BeiDou-2/Compass:A Perspective from Asia[J]. Journal of the Chinese Institute of Engineers, 2009, 32(5):679-689 |
| [5] | Yang Xinchun, Li Zhenghang, Wu Yun. The Performance Analysis of Constellation and XPL for Compass[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40:68-72(杨鑫春, 李征航, 吴云. 北斗卫星导航系统的星座及XPL性能分析[J]. 测绘学报, 2011, 40:68-72) |
| [6] | Han Yanben, Ma Lihua, Qiao Qiyuan, et al. Selection of Satellite Constellation Framework of CAPS[J]. Science in China, 2009, 3:458-471(韩延本, 马利华, 乔琪院, 等. 中国区域卫星定位系统星座布局的选择[J]. 中国科学, 2009, 3:458-471) |
| [7] | China Satellite Navigation Office, BeiDou Navigation Satellite System Signal in Space Interface Control Document Open Service Signal B1I (Version 1.0)[R]. Beijing:China Satellite Navigation Office, 2012(中国卫星导航系统管理办公室. 北斗卫星导航系统空间信号接口控制文件公开服务信号B1I(1.0 版)[R]. 北京:中国卫星导航系统管理办公室, 2012) |
| [8] | Kong Xiangyuan, Guo Jiming, Liu Zongquan. Foundation of Geodesy[M]. Wuhan:Wuhan University Press, 2005(孔祥元, 郭际明, 刘宗泉.大地测量学基础[M]. 武汉:武汉大学出版社, 2005) |
| [9] | Wei Ziqing. China Geodetic Coordinate System 2000 and Its Comparison with WGS84[J]. Journal of Geodesy and Geodynamics, 2008, 28(5):1-5(魏子卿. 2000中国大地坐标系及其与WGS84的比较[J]. 大地测量与地球动力学, 2008, 28(5):1-5) |
| [10] | Wei Ziqing, Ge Maorong. Mathematic Model of GPS Relative Positioning[M]. Beijing:Surveying and Mapping Press, 1998(魏子卿, 葛茂荣. GPS相对定位的数学模型[M]. 北京:测绘出版社, 1998) |
| [11] | Liu Huijie, Zhang Naitong. Research on Constellation Visibility for Global Navigation Satellite System[J]. Systems Engineering and Electronics, 2000, 22(5):23-25(刘会杰, 张乃通. 全球导航卫星系统的星座可见性研究[J]. 系统工程与电子技术, 2000, 22(5):23-25) |
| [12] | Deng Chenlong, Tang Weiming, Liu Jingnan, et al. Reliable Single-epoch Ambiguity Resolution for Short Baselines Using Combined GPS/BeiDou System[J]. GPS Solutions, DOI 10.1007/s10291-013-0337-5 |
 2015, Vol. 40
2015, Vol. 40


