文章信息
- 汤青慧, 唐旭, 崔晓晖, 胡石元, 刘耀林
- TANG Qinghui, TANG Xu, CUI Xiaohui, HU Shiyuan, LIU Yaolin
- 基于动态通达网络模型的最优航程规划方法
- Optimal Voyage Planning Strategies Based on a Dynamic Access Network Model
- 武汉大学学报·信息科学版, 2015, 40(4): 521-528
- Geomatics and Information Science of Wuhan University, 2015, 40(4): 521-528
- http://dx.doi.org/10.13203/j.whugis20140387
-
文章历史
- 收稿日期:2014-05-15
2. 武汉大学资源与环境科学学院, 湖北 武汉, 430079;
3. 武汉大学国际软件学院, 湖北 武汉, 430079;
4. 纽约理工学院工程与计算机科学系, 美国 纽约, 11360
2. School of Resource and Environment Science, Wuhan University, Wuhan 430079, China;
3. International School of Software, Wuhan University, Wuhan 430079, China;
4. School of Engineering and Computing Science, New York Institute of Technology, New York 11360, US
目前,每年约70亿吨的货物(约占全球贸易总量的90%)通过海洋运输,船舶租金和燃料等成本每天累积成千上万美元[1],航线安全和高效的重要性不言而喻。从文献[2, 3, 4, 5]可以看出,航程规划一直是近20年来海洋运输的研究热点。
根据环境信息和船舶状况,航程规划可分为静态规划和动态规划两类[6]。静态规划主要是基于已知的海域港口、地形和水深等信息,以避让静态碍航物与实现最短航线设计为目标。典型算法包括基于网格数据的邻域二分查找方法[7]、惩罚算法[8]、迷宫算法[9],基于矢量数据和空间几何解析[10]的航路二叉树[11]及递归改进搜索算法[12]、遗传算法[13],基于已知经验航线网络的A*算法[14]、Dijkstra算法[15]等。环境不变性是静态规划的前提假设,故前述研究仅限于起航前的计划航线搜索及优化。动态规划则需要考虑水文气象、突发事件等环境综合因素进行最优航线设计。但综合分析动态规划相关的随机动态网络规划方法[16]、船舶失速数值方法[17]以及基于滚动时域的启发式遗传搜索算法[18]等典型方法可知,环境因素及其动态变化产生的碍航特征并未得到系统分析,且实际航行中对计划航线进行动态修正和决策的场景研究也较少见。
安全性、可达性和经济性是航程计划制定时需要综合考虑的要素。本文通过将经验航线与海域实时动态环境信息叠加,构建包含时序禁航信息的动态通达网络模型,在此基础上考虑航速、油耗等船舶航行能力约束,按照“优度递减”的策略设计一种海域环境变化情景下的最优航程动态规划方法,为航船舶的续航、改航和停靠等后续航程计划的制定提供决策支持。 1 动态通达网络模型 1.1 动态通达网络定义
动态通达网络是在由港口集、经验航线集构建的静态网络基础上,叠加海域中灾害性天气和管制等海域限制因素对局部航线的通行影响,拓扑重构得到的弧段具有动态通达特征的一种网络模型。动态通达网络G(V,E)的要素定义如下:
1) 网络结点集V。V中的网络结点vi是港口集H[港口编号]、航线集L自身的交点集K[航线编号1,航线编号2]、航线集L与碍航区O的交点集B[碍航区编号]等三类点集的并集,其属性项定义为vi[结点编号,类型编码,港口编号,航线编号1,航线编号2,碍航区编号,影响碍航区序列]。其中,根据结点来源,类型编码分别用“H”、“K”和“B”区分,影响碍航区序列则以“,”为分隔符存储多个包含结点的碍航区编号,其他属性项内容则分别与3类点集的对应属性项内容一致。
2) 网络弧段集E。E中的网络弧段ei是航线集L[航线编号]中航线被结点集合K、B分割后生成的航线段,其属性项定义为ei[弧段编号,结点编号1,结点编号2,航线编号,弧段长度,禁航时段序列]。其中,结点编号1和结点编号2分别存储弧段端点对应的结点编号;航线编号则与弧段所在航线的对应属性一致;禁航时段序列采用分隔符“;”将多个碍航区的分段影响时间信息连接成一维序列化字符串存储,而单个禁航时段的具体格式为“(序号,碍航区编号,禁航开始时间,禁航结束时间)”。
由定义可知,动态通达网络模型实现了空间拓扑及环境影响等多源信息的网络集成,除了具备静态网络中的结点-弧段拓扑关系外,网络结点来源具有多样性,网络弧段通达具有动态性。这使得本文研究的航程决策分析区别于传统静态航线网络分析。 1.2 碍航区多边形提取
碍航区指对船舶安全通行产生影响而需要避离的障碍区域,其动态变化是导致航线通达性改变的主要因素。根据碍航区是否具有空间移动性,将其分为静止碍航区和移动碍航区。
1) 静止碍航区。根据出现时间的持续性,静止碍航区分为临时性和永久性两类。前者如军事禁航区、季节性渔场、能见度管制等,后者如岛礁、浅滩、沉船等。提取这些区域边界的特征点地理坐标,生成静止碍航区多边形集合 Os={ois,1≤i≤m}。m为静止碍航区个数,ois的生存周期为[ttk,tke]。
2) 移动碍航区。台风等极端天气在空间上沿可预测方向以一定的作用半径移动,进而形成移动碍航区OD={oDk,1≤k≤n}(n为碍航区中心个数)。移动碍航区的描述参数包括初始时刻中心坐标(φk,λk)、影响半径rk、移向Ck、移速vk,其在时段[tsk,tke] 的空间影响范围可以通过移动轨迹缓冲带计算得到的多边形来表示。
1.3 动态通达网络建立
动态通达网络的实时构建是快速、有效整合航程规划所需信息的基础算法,是将碍航区与静态航线网络叠加,确定航线禁止航行时间段的过程,具体如图 1所示。
 |
| 图 1 动态通达网络的建立流程Fig. 1 Building Processes of Dynamic Access Network |
动态通达网络建立包括4个技术环节:(1)静态网络构建。将港口间所有航线进行相交运算得到交点集 K和航线段集合L1,与港口集H一起构建静态网络。(2)碍航区分割航线。将静态碍航区和动态碍航区的多边形与航线段集合L1进行叠加,对如下两种情况分别进行处理:① 多边形包含航线段:将对应碍航区的[碍航区编号]直接添加到航线段端点的属性项[影响碍航区序列]中;② 多边形与航线段相交:生成交点集B和打断相交航线,航线段集合L1变为L2,将对应碍航区的[碍航区编号]直接赋予交点的[碍航区编号]并同时将其添加到多边形包含的航线段端点属性项[影响碍航区序列]中。(3)航线网络拓扑重构。将三类点集H、K和B合并生成网络结点集V,将航线段集合L2作为网络弧段集E,搜寻网络弧段ei起始、终止结点的[结点编号]分别存入属性项[结点编号1]和[结点编号2]中,实现网络拓扑的构建。(4)弧段禁航时序提取。根据弧段[结点编号1]和[结点编号2]在V中检索对应结点,提取结点的[影响碍航区序列]。当同一碍航区编号在起始和终止结点的[影响碍航区序列]中都出现时,表明该航线段受到碍航区影响。当影响碍航区为静态时,在该弧段的[禁航时段序列]中添加一个根据碍航区编号和其生存周期[tsk,tke]生成的禁航时段。当影响碍航区为动态时,则需要考虑其预报的移动特性计算影响弧段的禁航时段。
如图 2所示,以碍航区轨迹线上的点 (φk,λk)为中心,rk为影响半径做缓冲区C,分别计算C与弧段进入相切的时间ts(图 2(a))和离开相切的时间te(图 2(c)),向该弧段[禁航时段序列]中添加时间段为[ts,te]的禁航时段。
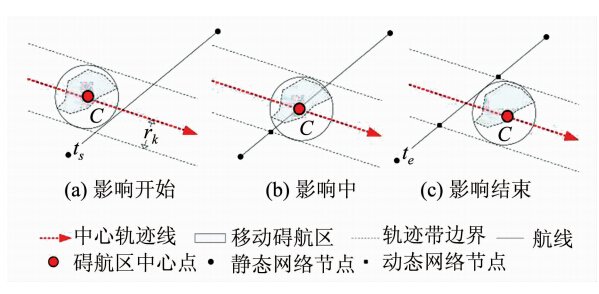 |
| 图 2 移动碍航区影响弧段的禁航时段Fig. 2 Time Segment of Sailing Prohibited by the Influence of Mobile Obstacle |
局部海域变化情景下的航程规划的实质是按照一定的约束准则在动态通达网络G(V,E)中开展路径寻优,并设计4类优度逐级递减的航程规划方案判别的算法过程。
1) 规划参数的初始化。除了需要按§1中 方法构建动态通达网络 G(V,E)外,还需要以下 规划参数:① 计划航线Lp即G(V,E)中连接出发港hs和目的港ht的路径;② 决策时点,为获取气象信息进行决策分析的时点t0,对应时点船的空间位置P0;③ 舰船性能参数,主要指船舶的续航能力:假设船舶油储备量为Q,以经济航速V航行的单位油耗为F(V),则续航能力A=Q/F(V)。
2) 三种约束准则建立。为实现航程安全性、可达性和经济性,航线规划需遵循三个准则。(1) 航线通达准则:保证船舶到达新规划航线中每个航段的起始端点时,航段都是通畅的;(2)续航约束准则:新规划航线总长度不得超过舰船的续航能力;(3)航线择优准则:新规划航线应是所有可选航线中最短的。
3) 优度递减决策过程。沿计划航线继续前行(续航)、选择新的最短绕行航线(改航)、选择最佳邻港进行停靠搜索(停靠)或原地等待救援是4类优度递减的船舶应对极端天气的决策策略。最优航程规划的决策过程遵循“择优不成则退而求其次”的原则进行。
具体技术流程如图 3所示。
 |
| 图 3 最优航程规划的技术流程图Fig. 3 Technology Flowchart for Optimal Voyage Planning |
如图 3所示,最优航程规划流程中总共包括航程通达性的判断算法、航线改变局部绕行算法、最短绕行航线搜索算法和最佳停靠邻港搜索算法等4个算法。 2.2.1 航程通达性的判断算法
航程通达性判断是确定船舶经过航线上任一弧段时,航行是否受到碍航区影响的过程,这是决定后续航程是否需要调整的重要依据。具体方法如下:(1)设拟航行航线的航线段序列为 Ek{e1,e2,…,ek},初始化ei通达性指示变量flagi=0;(2)设当前船位为P0,航速为V,决策转向时间为t0,计算当前船位P0沿航线到航线段ei起点的累计距离Di,则船舶到达时间为t1= t0+ Di/V;(3)设航线弧段ei的长度为di,则船舶离开航线段终点的时间t2= t1 +di/V,确定航线段ei的拟通行时段Ti[t1,t2];(4)提取航线段ei的[禁航时段序列],分段解析获取禁航时间段序列F{F1,F 2,…,F t},循环判断Ti与Fi的时间区间是否相交,如果相交,则令flagi=1;(5)对航线所有航线段进行步骤(2)~(4)的计算判断,并对所有flagi值(1≤i)求并,若结果为1,航程不通达,反之,通达。
2.2.2 航线改变局部绕行算法航线改变局部绕行算法是要在避开碍航区O的情况下,获取船舶位置P0的多条邻近航线,并确定邻近航线上距离P0最近的点构成转向点集合S。参照文献[10]思想,设计算法如下:(1)以当前位置P0为中心,选取一个较小的半径做缓冲区,获取邻近航线段集合Lk{l1,l2,…,lk};(2)在邻近航线段li上取P0的最近点P1,以连线P0P1作为可航渡的测试线;(3)如果连线 P0P1与O中碍航区均不相交,则船舶可以直接通过P0P1绕行到航线段li上;否则,在距P0最近的碍航区om的边界上寻找一个点Pt,使P0P1与P0Pt之间的方位差最大,由Pt替代P0,递归进行步骤(3),直到P0P1之间不存在碍航区;(4)记录所有邻近航线上距离P0最近的点P1i到S中,为最短绕行航线搜索算法提供基础数据。
2.2.3 最短绕行航线搜索算法最短绕行航线搜索算法主要是在§2.2.2局部绕行计算结果的基础上,求解船舶位置P0到目的港ht的最短可通达航线。具体方法如下。
1) 对任一航线转向点P1i,在动态通达网络G(V,E)上采用图论中深度优先遍历算法(DFS)[19],搜索P1i至目的港ht的所有路径,按照§2.2.1算法对所有路径进行通达性判断,形成可连通的路径集合Ri。
2) 在集合Ri中检索长度最短的路径,将路径长度与§2.2.2中计算得到的对应P0P1i长度相加,得到P0-P1i-ht的最短航线距离。
3) 对集合S{P11,P12,…,P1k}中所有邻近航线转向点都按照步骤(1)~(2)计算,得到P0- P1i -ht的最短航线距离,建立最短航线集合SL,从中找出最短者为船舶位置P0到目的港ht的最短可通达航线Sl。
4) 比较Sl航线长度d与船舶续航能力A。如果d
最佳停靠邻港搜索算法在续航能力不足绕行失败的情况下执行,目的在于确定一个最佳停靠港口供船舶增加补给,以保证船舶有足够的续航能力沿绕行航线到达目的港。一般基于两个原则进行邻港的搜索:(1)宽度搜索优先原则:分别在§2.2.3的最短航程集合Se中每一条路径上,搜寻距离船舶位置 P0最近的网络结点(类型编码=“H”);(2)深度搜索优先原则:在§2.2.3的最短可通达航线Sl上,搜寻距离船舶位置P0最近的网络结点(类型编码=“H”)。 2.3 方法实现
采用ESRI的Personal GeoDatabase存储本文涉及的底图、静态网络、碍航区、动态通达网络等数据,并使用ArcMap建立工程OVPS.mxd进行数据组织。利用C#和ArcObjects开发组件DANM.dll实现本文研究的规划算法,并在ArcMap中打开OVPS.mxd和加载DANM.dll执行规划方法的实验。 3 实验与分析 3.1 场景模拟
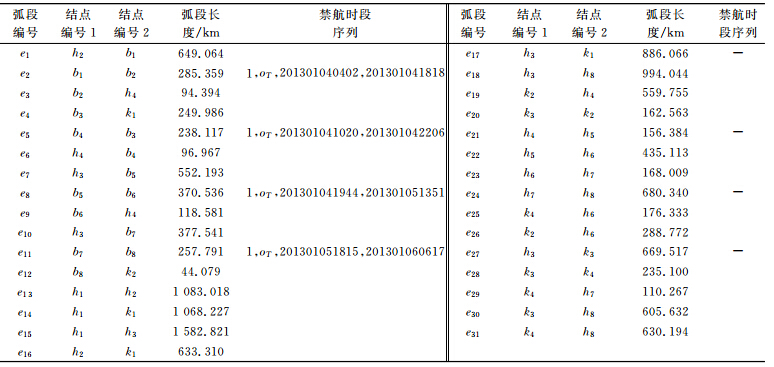
1) 静态航线网络。本文以东南亚海域为例,根据大洋航路图、航路设计图等资料选取香港( h1)、马尼拉(h2)、胡志明(h3)、哥打基纳巴卢(h4)、文莱(h5)、诗巫(h6)、古晋(h7)、新加坡(h8)8个主要港口和连接港口的15条已知经验航线。其中,航线l(h1,h4)与l(h2,h3)、l(h3,h6)与l(h4,h8)、l(h3,h7)与l(h4,h8)、l(h3,h7)与l(h6,h8)分别相交于k1、k2、k3、k4。构建的静态航线网络(见图 4(a))包括网络结点12个(H类8个和K类4个)、网络弧段23条,拓扑信息如表 1所示。
 |
| 图 4 船舶航程规划的场景数据及规划结果Fig. 4 Scene Data and Results of Ship Voyage Planning |
| 弧段编号 | 起结点 | 终结点 | 弧段编号 | 起结点 | 终结点 |
| 11 | h1 | h2 | 113 | h5 | h6 |
| 12 | h1 | k1 | 114 | h6 | h7 |
| 13 | h1 | h3 | 115 | h7 | h8 |
| 14 | h2 | k1 | 116 | k2 | h4 |
| 15 | h3 | k1 | 117 | k3 | k2 |
| 16 | h2 | h4 | 118 | h6 | k4 |
| 17 | h4 | k1 | 119 | h3 | k3 |
| 18 | h3 | h4 | 120 | k3 | k4 |
| 19 | h3 | k2 | 121 | k4 | h7 |
| 110 | k2 | h6 | 122 | h8 | k3 |
| 111 | h3 | h8 | 123 | k4 | h8 |
| 112 | h4 | h5 |
2) 碍航区域数据。以2013年菲律宾西部海域苏禄海海面生成的台风“清松”为例,参数为:1月3日20时,台风中心位置(9.1°N,119.5°E);预计1月7日20时,台风中心位置(6.2°N,108.1°E),根据航迹计算公式推算得到台风未来96 h的移动方向 C为 75 °SW、平均移速v为18.8 km/h,7级风圈半径约为120 km(见图 4(b))。
3) 动态通达网络。按§1所述方法将台风运动轨迹带与静态航线网络叠加,得到包含20个网络结点(H类8个、K类4个、B类8个)、31条网络弧段(4条受碍航区影响)的动态通达网络(见图 4(b)),拓扑信息如表 2所示。
4) 舰船计划航线。某船从新加坡( h8)至香港(h1),计划航线由弧段e30、e20、e19、e6、e5、e4、e14 顺次连接而成。航速35 km/h,单位油耗2.491 7 t/h,续航能力A为2 500 km(见图 4(a))。
5) 决策时点与需求。以船舶接收到台风预报信息的时间1月3日08:00为决策时点,对应的决策船舶位置为P0(见图 4(b)),现需要基于前述数据信息对船舶未来航程进行规划。 3.2 规划结果
1) 计划航线通达判断。计划航线上弧段 e5(b4 b3)受台风影响,禁航时段为(201301041020,201301042206),从P0至b4、b3 的航线长度分别为1 010.524 8 km、1 248.641 6 km;船舶从P耗0航至b4、b3时分别为28 h 43 min、35 h 29 min,在e5拟通行时段为(201301041242,201301041929)。对比禁航和通行时段,可知时间重叠。据§2.2.1算法知该计划航线受台风影响不可通行。
2) 最短绕行航线搜索。按照§2.2.2算法,在P0点以半径150 km搜索得到邻近航 线Lk{e18,e30}并确定对应转向点集合S{ P0,P1}。按照§2.2.3算法,对P0至目标港口h1的100条连通航线进行通达性判断,获取59条通达航线中最短的航线A:P0-k3-h3-h1(见图 4(c));对P1点至目标港口h1的122条连通航线进行通达性判断,选取88条通达航线中最短的航线B:P1-k4-k3-h3-h1(见图 4(d))。将两条最短航线加入最短绕行航线集Se,比较长度得到最佳绕行航线为P0-k3-h3-h1(表 3),绕行长度为2 443.57 km。
| 序号 | 邻近航线 | 转向点P | DP0-P/km | 连通路径途经结点 | 目的港 | dP-h1/km | ∑ d/km | 是否选择 |
| ① | e18(k3-h8) | P0 | 0 | k3-h3 | h1 | 2 443.57 | 2 443.57 | √ |
| ② | e30(k4-h8) | P1 | 138.49 | k4-k3-h3 | h1 | 2 717.33 | 2 855.82 |
3) 最佳停靠邻港搜索。船舶满载续航能力2 500 km,在h8P0段已航行414.4 km,而上一步计算的最佳绕行航线长2 443.57 km,大于剩余续航能力2 085.6 km,因此应考虑选择合适邻港停靠增加补给。由§2.2.4算法,按照深度优先原则在最佳绕行航线P0-k3-h3-h1上搜索距离P0最近的港口为h3,得到P0-k3-h3长度为1 275.16 km,满足船舶的续航能力。因此,该船应执行停靠h3增加补给后续航到达h/1的方案。 4 结 语
海域水文和气象信息很难做出长期准确的预报,基于可预报的海域环境动态变化信息,获取后续的最优航程计划是远洋航行和海洋指挥救援的重要技术需求。本文构建的动态通达网络模型很好地描述了军事禁航区、季节性渔场、能见度管制等临时性的和岛礁、浅滩、沉船等永久性的静止碍航区以及台风等极端天气形成的移动碍航区对航线网络的动态阻隔影响特征。在此基础上,按照“优度递减”策略设计的包含计划航线通达分析(续航决策)、最短绕行航线搜索(改航决策)、最佳停靠邻港搜索(停靠决策)等步骤的最优航程规划方法,顾及了航线通达、续航可行和航线最短等约束,很好地模拟了实际航行中因为规避环境动态变化影响对计划航线进行动态修正的决策场景。本文方法能够实现航程安全性、可达性和经济性的最佳结合,实验算法也验证了规划技术路线的可操作性。后续研究中,将综合考虑碍航区动态变化、大风浪中船舶失速、船舶停靠等候避让决策等多种要素的综合影响,使航程规划方法更加科学、合理。
| [1] | UUCTAD. Review of Maritime Transportation, Technical Report[R]. UNCTAD, 2009 |
| [2] | Ronen D. Ship Scheduling:the Last Decade [J]. European Journal of Operational Research, 1993, 71(3):325-333 |
| [3] | Ronen D. Cargo Ships Routing and Scheduling:Survey of Models and Problems [J]. European Journal of Operational Research, 1983, 12(2):119-126 |
| [4] | Christiansen M, Fagerholt K, Ronen D. Ship Routing and Scheduling:Status and Perspectives [J]. Transportation Science, 2004, 38(1):1-18 |
| [5] | Christiansen M, Fagerholt K, Nygreen B, et al. Handbooks in Operations Research and Management Science[M].Germany:Springer-Verleg, 2007 |
| [6] | Metea M B. Planning for Intelligence Autonomous Land Vehicles Using Hierarchical Terrain Representation [C]. IEEE Int. Confon on Robotics and Automation, Raleigh, North Carolina, 1987 |
| [7] | Li Yuanhui, Pan Mingyang, Wu Xian. Automatic Creating Algorithm of Route Based on Dynamic Grid Mode[J]. Journal of Traffic and Transportation Engineering, 2007, 7(3):34-39(李源惠, 潘明阳, 吴娴. 基于动态网格模型的航线自动生成算法[J]. 交通运输工程学报, 2007, 7(3):34-39) |
| [8] | Rafal S. A New Method of Ship Routing on Raster Grids, with Turn Penalties and Collision Avoidance[J]. The Journal of Navigation, 2006, 59(1):371-384 |
| [9] | Chang, K Y, Jan G E, Parberry I. A Method for Searching Optimal Routes with Collision Avoidance on Raster Charts[J]. The Journal of Navigation, 2003, 56(3):371-384 |
| [10] | Zhang Lihua, Zhu Qing, Liu Yanchun, et al. A Method for Automatic Routing Based on ECDIS[J]. Journal of Dalian Marine University, 2007, 33(3):109-112 (张立华, 朱庆, 刘雁春, 等. 电子海图平台下的航线自动设计方法[J]. 大连海事大学学报, 2007, 33(3):109-112) |
| [11] | Wang Zhu, Li Shujun, Zhang Lihua, et al. A Method for Automatic Routing Based on Route Binary Tree[J].Geomatics and Information Science of Wuhan University, 2010, 35(4):407-410 (汪柱, 李树军, 张立华, 等. 基于航路二叉树的航线自动生成方法[J]. 武汉大学学报·信息科学版, 2010, 35(4):407-410) |
| [12] | Cao Hongbo, Zhang Lihua, Jia Shuaidong, et al. An Improved Method for Automatically Building Shortest Route Based on Electronic Chart[J].Geomatics and Information Science of Wuhan University, 2011, 36(9):1 107-1 110(曹鸿博, 张立华, 贾帅东, 等. 电子海图最短距离航线自动生成的改进方法[J].武汉大学学报·信息科学版, 2011, 36(9):1 107-1 110) |
| [13] | Chen Huafeng, Ye Shiping, Huang Zhicai, et al. Ocean Scientific Survey Route Designing Method Syncretizing Triangulated Irregular Networks and Genetic Algorithm[J]. Journal of Zhejiang University(Engineering Science), 2009, 43(11):1 951-1 957 (陈华锋, 叶时平, 黄智才, 等. 融合不规则三角网和遗传算法的大洋科考航线设计方法[J]. 浙江大学学报(工学版), 2009, 43(11):1 951-1 957) |
| [14] | Wang Dechun, Chen Limin, Zhang Xiaofang. Selecting Ship's Optimum Route Using A* Algorithm[J]. Journal of Qingdao University (Natural Science Edition), 2005, 18(4):10-13 (王德春, 陈利敏, 张孝芳.基于A*算法的舰船最佳航线选择[J].青岛大学学报(自然科学版), 2005, 18 (4):10-13) |
| [15] | Wu Fengping, Zhu Baochun. A Method to Select Ship's Minimum-Propbability Line[J]. Jounal of Hohai University, 2001, 29 (1):77-79 |
| [16] | Bijlsma S J.On the Applications of the Principle of Optimal Evolution in Ship Routing[J].Journal of the Institute of Navigation, 2004, 51(2):93-100 |
| [17] | Li Yuanlin, Chen Hongbin. Design of Optimum Ship Route Using Weather Routing Techniques[J]. Journal of South China University of Technology(Natural Science), 1997, 25(12):65-69 (李远林, 陈宏彬.船舶最佳气象航线的设计[J].华南理工大学学报:自然科学版, 1997, 25(12):65-69) |
| [18] | Kang M H, Choi H R, Kim H S, et al. Development of a Maritime Transportation Planning Support System for Car Carriers Based on Genetic Algorithm[J]. Applied Intelligence, 2012, 36:585-604 |
| [19] | Wang Guiping, Wang Yan, Ren Jiachen. Graph Theory Algorithm Theory, Implementation and Applications [M]. Beijing:Peking University Press, 2011(王桂平, 王衍, 任嘉辰. 图论算法理论、实现及应用[M]. 北京:北京大学出版社, 2011) |
 2015, Vol. 40
2015, Vol. 40