文章信息
- 刘爱龙, 杜清运, 张东, 蔡忠亮, 李鹤元
- LIU Ailong, DU Qingyun, ZHANG Dong, CAI Zhongliang, LI Heyuan
- 嵌入式环境下全球尺度瓦片地图数据组织与索引机制
- Organization and Indexing Mechanism for Global Tile Map Data Under Embedded Environment
- 武汉大学学报·信息科学版, 2015, 40(4): 516-520
- Geomatics and Information Science of Wuhan University, 2015, 40(4): 516-520
- http://dx.doi.org/10.13203/j.whugis20140415
-
文章历史
- 收稿日期:2014-05-27
2. 地理信息工程国家重点实验室, 陕西 西安, 710054;
3. 西安测绘研究所, 陕西 西安, 710054;
4. 解放军信息工程大学地理空间信息学院, 河南 郑州, 450052
2. State Key Laboratory of Geo-information Engineering, Xi'an 710054, China;
3. Xi'an Research Institute of Surveying and Mapping, Xi'an 710054, China;
4. Institute of Geospatial Information, Information Engineering University, Zhengzhou 450052, China
瓦片地图是嵌入式地理信息系统中主要的一种地图数据类型,嵌入式环境下瓦片地图数据组织受到系统资源有限的限制。如何高效地进行组织和存储是嵌入式地理信息系统需要重点研究和解决的问题。
目前嵌入式地图数据组织模型研究主要集中于矢量数据组织[1, 2]方面。在瓦片数据组织方面,文献[3]给出了一种基于NoSQL数据库,以单个瓦片为单元对数据进行存储和检索的方法;文献[4]基于云计算环境提出了遥感影像瓦片数据组织模型,这些研究大都基于服务器端。文献[5]在嵌入式环境下,针对局部区域影像提出了基于四叉树索引的遥感影像瓦片金字塔数据模型。在全球尺度数据组织方面,作为三维数字地球表达的基本数据模型[6],全球离散网格模型是研究的一个热点。它用拟合格网来表达地球表面[7],对格网的剖分主要采用两种方式,一种基于正多面体和规则形状进行剖分[8, 9],另一种采用经纬度格网对地球表面进行划分[10, 11]。全球离散网格主要面向三维球面剖分,应用也以遥感信息多尺度表示与管理为主[12]。基于正多面体网格的分割方法具有层次性、全球连续性、可无限细分、不会改变形状等优点,但其地址码与地理坐标映射计算比较复杂,无法完全适应计算资源有限的嵌入式环境。基于经纬度的网格划分受球面影响,网格从低纬到高纬形状变化较大,难以适应以二维瓦片地图应用为主的嵌入式环境。
本文主要基于低功耗、电磁兼容且对操作系统与器件国产化有特殊要求的嵌入式环境进行研究,解决在内存、计算资源普遍较低的情况下,全球范围矢量地图和影像地图的栅格瓦片数据高效组织与调度。
1 嵌入式环境下瓦片数据组织约束模型
嵌入式系统具有内核小、实时性和可靠性要求高等特点,需尽可能地对系统软硬件进行裁剪[13],因此其内存、计算、存储和显示等系统资源非常有限。这种资源有限性使全球尺度瓦片地图数据的存储、快速检索和显示受到了较大约束。
按照嵌入式环境资源有限性与瓦片组织需求之间的关系,可定义如下约束模型:
定义1 嵌 入式资源限制条件变量U为一个五元组:
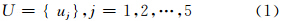
式中,u1表示嵌入式环境有限的内存资源限制;u2表示低主频的计算资源限制;u3表示较小的屏幕显示资源限制;u4表示数据读取速率限制;u5表示外部存储资源限制。
定义2 全球瓦片数据组织需求变量D为一个四元组
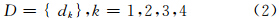
式中,d1表示瓦片可视化的多分辨率需求;d2表示全球瓦片TB级大数据量需求;d3表示几万到上百万的瓦片数量需求;d4表示瓦片数据快速检索与调用需求。
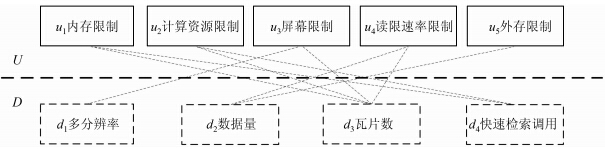
图 1给出了U、D之间的约束关系,按照约束关系,瓦片数据组织约束模型可定义如下:
|
| 图 1 瓦片数据组织约束关系模型 Fig. 1 Restrictive Relation Model of Tile Map Data Organization |
定义3 瓦片数据组织约束关系模型R
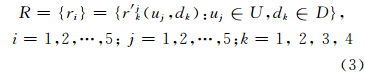
式中,ri表示有效约束关系,它由r′jk (uj,dk )决定,即第j个资源限制变量与第k个应用要求变量之间的关系决定。按照有效关系,可将约束关系归为5类。
1) r1{u1 |d3,d4},表示内存资源限制u1与调入内存瓦片数量d3、快速检索调用d4之间的约束关系。
2)r2{u2 |d3,d4},表示计算资源限制u2与瓦片数量d3、快速检索调用d4之间的约束关系。
3)r3{u3 |d1,d3},表示屏幕资源限制u3与瓦片多分辨率d1、瓦片数量d3之间的约束关系。
4)r4{u4 |d2,d3},表示数据读取速率u4与瓦片总数据量d2、瓦片数量d3之间的约束关系。
5) r5{u5 |d2},表示外存容量u5与总数据量d2的约束关系,可表示为 5 ≥ 2,即外存必须满足存储数据量要求。
2 嵌入式瓦片数据组织模型
瓦片金字塔组织模型是一种多分辨率层次模型[14],从瓦片金字塔的底层到顶层,分辨率越来越低,地理范围不变。这是一种较好的解决思路,但在资源有限的嵌入式环境下,不同的分级、分块策略和存储、检索机制会对效率和可视化效果产生非常大的影响。本文以分层、分块的金字塔模型为基础,按照上述限制条件,以栅格瓦片数据为例讨论数据组织模型,使其满足嵌入式环境下快速显示和层级间平滑过渡的要求。
2.1 瓦片数据逻辑组织模型
本文组织模型主要针对瓦片地图的二维可视化表达,瓦片地图采用球体-Mercator投影,投影后在纬度±85.05°进行切割,使全球成为在经纬度两个方向像素相等的正方形,并以20级不同的尺度和分辨率来分别构建。瓦片分割采取四象限递归“金字塔”剖分方式,按照式(4)的分割计算方法,对栅格数据进行分割组织。
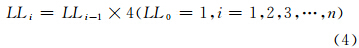
对全球框架下的单一类型瓦片数据,采用分级、分块的逻辑组织策略,以“瓦片集-放大层级-瓦片数据(行、列序)”的方式组织。其中,瓦片数据集包括各个层级全球范围的瓦片数据,瓦片按不同等级依次存储。
针对约束关系对 r1、r3和r4展开分析,可知嵌入式设备内存与显示范围有限,确定瓦片数据分块大小是问题的关键。
不考虑检索时间,调用和显示瓦片的数据量是影响可视化效率的主要因素。在内存资源 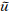 1与可用计算资源
1与可用计算资源 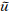 2一定时,设屏幕为正方形、瓦片尺寸为s,则需调用的瓦片数据量
2一定时,设屏幕为正方形、瓦片尺寸为s,则需调用的瓦片数据量 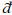 3与屏幕分辨率
3与屏幕分辨率 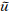 3、瓦片尺寸s存在如下关系:
3、瓦片尺寸s存在如下关系:
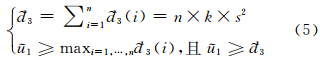
式中,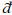 3(i)为需调入内存的第i个瓦片数据量; k为在忽略不同复杂程度瓦片数据变化情况下的单位面积瓦片数据量;n为需调用的瓦片个数,可表示为:
3(i)为需调入内存的第i个瓦片数据量; k为在忽略不同复杂程度瓦片数据变化情况下的单位面积瓦片数据量;n为需调用的瓦片个数,可表示为:
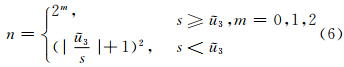
式(6)中,m的值取决于瓦片范围与屏幕显示范围的关系。
设E为屏幕有效显示数据量比例,则
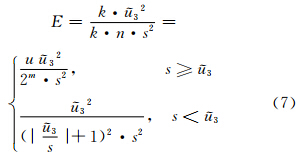
当s≥ 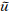 3时,采用悲观策略,m取最大值,E=1/4×
3时,采用悲观策略,m取最大值,E=1/4× 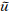 32/s2。由式(7)可推出,瓦片尺寸s越大,则有效显示比例越小,显示效率越低。若瓦片过小,则瓦片量呈几何倍数增长,根据约束关系r1、r2和r4,此时需降低瓦片检索和读取效率。依据嵌入式设备分辨率,瓦片大小取128像素×128像素或256像素×256像素,无效数据量对显示效率影响均在可容忍范围。瓦片的检索和读取效率,可通过高效的编码索引和存储机制来解决。
32/s2。由式(7)可推出,瓦片尺寸s越大,则有效显示比例越小,显示效率越低。若瓦片过小,则瓦片量呈几何倍数增长,根据约束关系r1、r2和r4,此时需降低瓦片检索和读取效率。依据嵌入式设备分辨率,瓦片大小取128像素×128像素或256像素×256像素,无效数据量对显示效率影响均在可容忍范围。瓦片的检索和读取效率,可通过高效的编码索引和存储机制来解决。
2.2 瓦片数据编码索引机制
受限制模型R中的限制关系r1和r2影响,瓦片数据的检索算法不能过于复杂。本文设计了二维线性编码方案对数据块进行编码,在提高检索效率的同时,减少检索的计算量。其基本思想为:将每一个既定等级栅格数据矩阵的左上角设为原点,垂直向下(向南)为Y轴方向,平行向右(向东)为X轴方向。则每个栅格块的编码可表示为 Lev-Ycol-Xraw,其中,Lev为级数,Ycol为该栅格块在Y轴的行数,Xraw为该块在X轴的列数,数值保持定长方式。
本文采用二维线性编码方式,使不同级次的栅格瓦片位置关系变得简单。瓦片的相邻层级间的缩放关系为编码的位移运算,平移对应编码的整数加减运算,可极大提高瓦片的计算速度和查询效率,较好地解决了 r1和r2的限制。
2.3 瓦片数据物理存储模型
限制关系r1、r2和r4存在如下关系: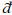 4→
4→ 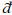 3/
3/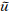 2,即瓦片检索调用效率
2,即瓦片检索调用效率 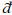 4与瓦片数量
4与瓦片数量 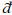 3成正比,与可用计算资源
3成正比,与可用计算资源 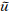 2成反比,在内存资源
2成反比,在内存资源 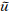 1和数据读取速率
1和数据读取速率 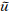 4一定时,瓦片数量越大,检索调用效率越低。
4一定时,瓦片数量越大,检索调用效率越低。
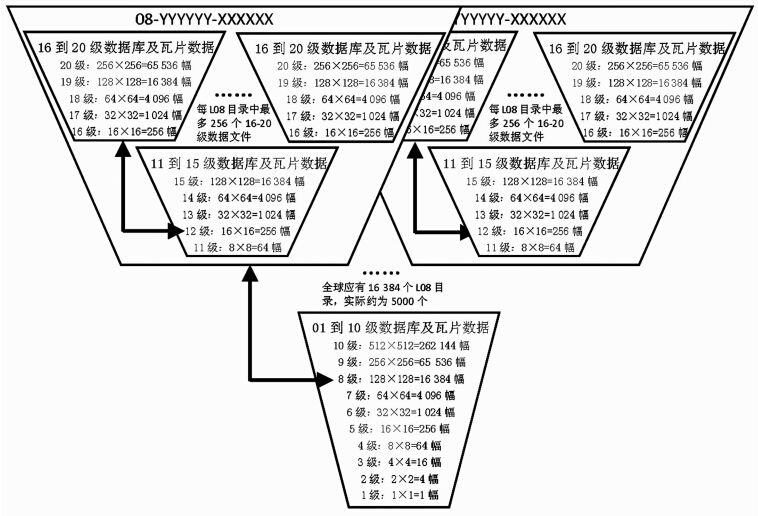
针对此限制关系,本文设计了基于范围的整合存储模型,对数据文件整合存储,使每个数据包中的瓦片数据量基本相同,减少巨量小文件对系统检索效率的影响。其基本思想为:将全球瓦片数据按照一定规则分割成若干数据库文件存储,并将不同数据库目录和文件跨卷存储到嵌入式设备和大型储存设备中,不同类型的瓦片数据采用统一的数据结构、文件格式和管理策略进行存储,以便更新嵌入式设备中的瓦片数据。图 2为物理存储模型示意图。
|
| 图 2 瓦片地图数据物理存储模型 Fig. 2 Physical Model of Tile Map Data Organization |
在图 2中,全球01~10级的某一类瓦片数据整合为一个嵌入式数据库文件,位于整个瓦片“金字塔”结构的底部;全球第11~20级的某一类瓦片数据被分为16 384个区域(称为L08数据库目录),每一个区域对应08级一个数据瓦片所覆盖的区域;在每一个L08数据库目录中,属于该范围的第11~15级瓦片数据存储为1个嵌入式数据库文件;而属于该范围的第16~20级瓦片数据按照L12瓦片覆盖范围被分割为256个嵌入式数据库文件,具体的文件数量由该区域高分辨率数据覆盖率决定,最多为256个。
3 实验与分析
本文提出的瓦片地图数据组织模型和索引机制在嵌入式测绘导航服务项目中得到检验和应用。采用的嵌入式终端为定制的北斗用户终端,主频为800 MHz,内存为512 MB,外存为容量64 GB SD卡,屏幕分辨率为1 024像素×768像素。实验数据包括全球区域1~13级栅格瓦片(影像图、线划图)数据,总数据量为51.3 GB,瓦片采用256像素×256像素大小分块。表 1为不同复杂度(数据量)瓦片平均每秒调用和显示效率实验结果。图 3为不同层级瓦片调用和显示效率实验结果,图 4为可视化效果。
| 不同复杂度单个瓦片平均数据量/KB | 每s调用瓦片数量/个 | 平均每s显示瓦片数量/个 |
| 65(较复杂) | 105 | 43 |
| 28(中等复杂) | 200 | 62 |
| 12(较简单) | 310 | 95 |
|
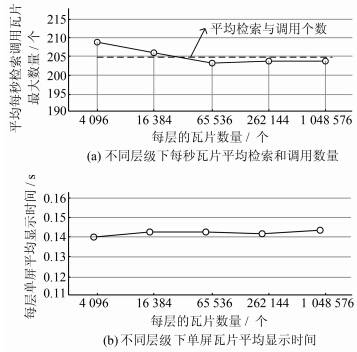
| 图 3 瓦片检索调用和显示效率 Fig. 3 Efficiency of Tile Map Query and Display |
|
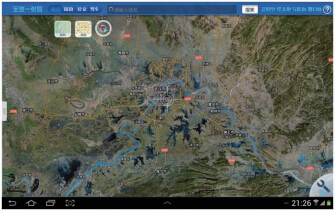
| 图 4 瓦片数据显示效果 Fig. 4 Effect Display of Tile Map |
从表 1可看出,瓦片数据量越大,则每秒检索与调用的瓦片数量越少。在瓦片平均数据量在65 KB的实验条件下,单个瓦片的平均检索与调用时间为0.009 s,每屏调用与显示平均时间为0.28 s;在瓦片平均数据量为12 KB的实验条件下,单个瓦片的平均检索与调用时间为0.003 s,每屏调用与显示平均时间为0.13 s。瓦片数据量对调用的结果产生较大影响的原因主要是由于嵌入式环境数据读取I/O速率的限制,使得数据量差异越大,读取时间差异越大。
图 3(a)为不同层级下平均每秒检索和调用的瓦片数量。结果表明,由于采用分包存储策略,不同层级瓦片所在数据包的文件大小均在1 GB 左右,因此不同层级瓦片每秒平均调用的瓦片数量均在205个左右,说明了该模型在检索和调用方面的均衡和高效性;图 3(b)为不同层级下单屏瓦片地图显示平均时间,在瓦片平均 数据量为30 KB左右时,不同层级的每屏瓦片调用和显示平均时间在0.142 s左右,满足漫游对连续性的要求。
图 4为影像瓦片地图可视化效果图。由图 4可以看出,本文采用的数据分级方式,能够比较清晰地展示地图内容。
表 2为在相同的实验环境下,本文模型与文献[5]中四叉树金字塔组织模型瓦片检索与调用的对比实验结果。
| 瓦片数量 | 本文方法 | 四叉树金字塔方法 |
| 4 096 | 207 | 142 |
| 16 384 | 206 | 113 |
| 65 536 | 204 | 96 |
| 262 144 | 204 | 74 |
表 2表明,在检索调度的效率方面,本文的瓦片组织模型明显优于文献[5]方法。本文模型的检索调度效率受瓦片数量影响不大,文献[5]中的模型随瓦片数量的增加,效率下降较明显。
上述实验表明,本文提出的瓦片地图数据组织模型能够比较好地适应计算和显示资源有限的嵌入式环境,显示效果和效率符合移动环境下用户地图阅读和浏览的要求。
4 结 语
针对内存、计算和屏幕资源都有限的嵌入式环境,本文在分析和构建嵌入式环境对瓦片数据组织约束模型的基础上,提出了一种满足资源有限环境的瓦片地图数据组织模型,并以栅格瓦片数据为例,阐释了模型的合理性和可行性。实验表明,该模型对嵌入式环境具有较好的适应性。本文所提出的瓦片数据组织模型可为嵌入式环境下移动地理信息应用提供一种有效的解决方案。
| [1] | Kashyap R L, Mohan L. An Object-oriented Knowledge Representation for Spatial Information[J]. IEEE Transaction on Software Engineering, 1988, 516:674 -681 |
| [2] | Hu Zeming, Yue Chunsheng, Wang Zhigang. Hybrid Model Design of Multiscale Map Data on Embedded GIS[J]. Journal of Information Engineering University, 2007, 8(4):493-496(胡泽明, 岳春生, 王志刚. 嵌入式GIS多比例尺地图数据混合组织模型设计[J]. 信息工程大学学报, 2007, 8(4):493-496) |
| [3] | Chen Chao, Wang Liang, Yan Haowen, et al. A Map Tiles Data Storage Technology Based on NoSQL[J]. Science of Surveying and Mapping, 2013, 38(1):142-143(陈超, 王亮, 闫浩文, 等. 一种基于NoSQL的瓦片地图数据存储技术[J].测绘科学, 2013, 38(1):142-143) |
| [4] | Lai Jibao, Luo Xiaoli, Yu Tao, et al. Remote Sensing Data Organization Model Based on Cloud Computing[J]. Computer Science, 2013, 40(7):80-83 (赖积保, 罗晓丽, 余涛, 等. 一种支持云计算的遥感影像数据组织模型研究[J]. 计算机科学, 2013, 40(7):80-83) |
| [5] | Wang Tao, Deng Xueqing, Dai Chenguang, et al. A Remote Sensing Image Data Model for PDA and Its Display Algorithm[J]. Science of Surveying and Mapping, 2009, 34(2):184-186(王涛, 邓雪清, 戴晨光, 等. 一种用于PDA的遥感影像数据模型及其显示算法研究[J]. 测绘科学, 2009, 34(2):184-186) |
| [6] | Goodchild M F. Discrete Global Grids:Retrospect and Prospect [J]. Geography and Geo-Information Science, 2012, 28(1):1-6 |
| [7] | Bai Jianjun, Zhao Xuesheng, Chen Jun. Indexing of Discrete Global Grids Using Linear Quadtree[J]. Geomatics and Information Science of Wuhan University, 2005, 30(9):805-808(白建军, 赵学胜, 陈军. 基于线性四叉树的全球离散格网索引[J]. 武汉大学学报·信息科学版, 2005, 30(9):805-808 |
| [8] | Alborzi H, Samet H. Augmenting SAND with a Spherical Data Model [C]. The First International Conference on Discrete Global Grids, Santa Barbara, 2000 |
| [9] | White D. Global Grids from Recursive Diamond Subdivisions of the Surface of an Octahedron or Icosahedrons[J]. Environmental Monitoring and Assessment, 2000, 64(1):93-103 |
| [10] | Ottoson P, Hauska H.Ellipsoidal Quadtrees for Indexing of Global Geographical Data[J]. Int. J. Geographical Information Science, 2002, 16(3):213-226 |
| [11] | Tobler W, Chen Z.A Quadtree for Global Information Storage[J].Geographical Analysis, 1986, 18(4):360-371 |
| [12] | Tong Xiaochong, Ben Jin, Zhang Yongsheng. Expression of Spherical Entities and Generation of Voronoi Diagram Based on Truncated Icosahedron DGG[J]. Geomatics and Information Science of Wuhan University, 2006, 31(11):966-970(童晓冲, 贲进, 张永生, 等. 基于二十面体剖分格网的球面实体表达与Voronoi图生成[J]. 武汉大学学报·信息科学版, 2006, 31(11):966-970 |
| [13] | Zhang Dong, Qian Depei, Wang Jiayao, et al. Map Data Denotation and Parallel Display Algorithm in Embedded Navigator[J]. Geomatics and Information Science of Wuhan University, 2007, 32(4):343-346(张东, 钱德沛, 王家耀. 嵌入式环境下导航地图数据表示和并行调度显示算法[J]. 武汉大学学报·信息科学版, 2007, 32(4):343-346) |
| [14] | Du Qingyun, Yu Changbin, Ren Fu. Organization Tile Map Data Based on Nested Pyramids Model[J]. Geomatics and Information Science of Wuhan University, 2011, 36(5):564-567 (杜清运, 虞昌彬, 任福. 利用嵌套金字塔模型进行瓦片地图数据组织[J]. 武汉大学学报·信息科学版, 2011, 36(5):564-567 |
 2015, Vol. 40
2015, Vol. 40


