文章信息
- 袁胜古, 潘俊, 应荷香, 王密
- YUAN Shenggu, PAN Jun, Ying Hexiang, WANG Mi
- 一种改进的GVF蛇模型水域矢量边界更新方法
- A Method of Water Vector Edge Updating Based on Improved GVF Snakes Model
- 武汉大学学报·信息科学版, 2015, 40(4): 503-509
- Geomatics and Information Science of Wuhan University, 2015, 40(4): 503-509
- http://dx.doi.org/10.13203/j.whugis20140026
-
文章历史
- 收稿日期:2014-01-07
2. 地球空间信息技术协同创新中心, 湖北 武汉, 430079;
3. 浙江省地理信息中心, 浙江 杭州, 310012
2. Collaborative Innovation Center for Geospatial Technology, Wuhan University, Wuhan 430079, China;
3. Geomatics Center of Zhejiang Province, Hangzhou 310012, China
矢量边界数据是GIS(地理信息系统)数据库的重要组成部分,其现势性是GIS有效运行的前提。由于经济发展及自然环境的变化,地表不断发生变化,GIS矢量数据需要及时更新以满足生产建设的需要。传统的基于人工进行矢量边界数据的更新方法既费时又昂贵。由于遥感影像现势性越来越高,基于遥感影像对GIS数据库中矢量边界数据更新的方法越来越受到重视,利用遥感影像并结合已有GIS矢量数据对GIS数据进行更新也成为一个热点研究领域[1, 2, 3, 4, 5]。
蛇模型可以将图像数据、初始边界、理想边界以及先验知识结合起来进行演化,使初始边界演化收敛于理想边界,适合利用历史矢量边界数据与现有遥感影像对矢量边界数据进行更新[6]。利用GIS中历史矢量边界数据作为蛇模型初始边界位置,结合现势性更高的遥感影像,通过初始边界位置的演化实现矢量边界数据的更新。Fortier等[7]使用已有GIS道路数据为初始边界位置,结合高分辨率遥感影像,采用蛇模型对道路数据库进行修正与更新。韩敏等[8]提出了一种分组式蛇模型的GIS矢量边界更新方法。唐伟等[9]使用梯度向量流(gradient vector flow,GVF)蛇模型解决传统蛇模型道路凹陷位置有效逼近问题,实现了道路轮廓提取。周毅等[10]基于高分辨率DEM数据,使用坡面汇流方向场改进蛇模型中的梯度矢量流场,提出了一种改进的蛇模型黄土地形沟沿连接算法。以上方法在使用蛇模型或GVF蛇模型中,大多使用单波段信息,或者将多波段影像转化为亮度图像后再处理,没有完全利用多波段的色彩信息,在计算梯度时可能会出现偏差,最终造成蛇模型或者GVF蛇模型不能收敛到目标边缘,不能准确反映地物的真实边界。针对这个问题,本文提出了一种改进的GVF蛇模型水域矢量边界更新方法。
1 GVF 蛇模型的数学模型描述
经典蛇模型可以使用如下参数方程来表示[6]:
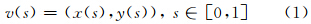
蛇模型的思想是设计一个平面曲线泛函,使目标轮廓曲线为该泛函的最小值。 Kass等人设计能量泛函如下:
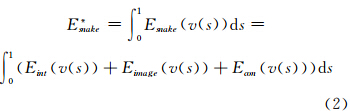
式中,Eint(v(s)为内部能量;Eimage(v(s))为图像能量;Econ(v(s))为条件能量;一般把Eimage(v(s))与Econ(v(s))统称为外部能量。内部能量定义如下:

式中,vs(s)和vss(s)分别表示v(s)的一阶导数和二阶导数;α(s)和β(s)分别为一阶导数和二阶导数的权重参数,用于控制曲线的连续性和光滑性。
为了解决经典蛇模型对初始轮廓敏感、捕捉范围小等缺点,Xu[11, 12]提出了GVF 蛇模型,定义了新的外力场,即梯度向量流场,用于替代Kass蛇模型中的外力场,GVF以求取泛函ε最小值来获取:

式中,V=(u(x,y),v(x,y))为梯度向量流场;f为图像边缘图;∇f为图像边缘图梯度。通过分析文献[11, 12]对于GVF的定义可以看出,当∇f比较小时,能量函数主要由第一项μ(u2x+u2y+v2x+v2y)向量场的偏微分平方和决定;当∇f比较大时,能量函数由第二项 |∇f| 2 |V-∇f| 2决定。实质上,GVF 就是在边缘处保留原外力场的基础上,进行平滑扩散,从而增大了捕捉范围。参数μ越大,GVF越平滑,捕捉范围也就越大。
根据变分法,求解式(4)泛函最小值,即求解欧拉方程组:
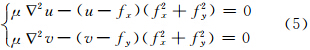
式中,fx与fy分别为图像边缘图水平与垂直方向的梯度,即∇f=(fx,fy)。
2 改进GVF 蛇模型边界更新方法
GVF蛇模型一般用于灰度图像,对背景与目标分明的图像具有非常好的效果。本文所使用遥感影像为彩色影像,若是简单地将彩色影像变换为灰度影像,不能取得好的效果。因为彩色影像变换为灰度影像后,原有彩色影像中由于颜色差异形成的边缘在灰度影像中可能不能识别或者不明显。这种情况下计算的GVF场不能很好反映原始彩色影像中的梯度场。
为了解决此问题,本文结合彩色边缘算法对GVF 蛇模型中的GVF场泛函进行改进,即对式(4)中图像边缘图f进行重新定义。传统方法图像边缘图对单波段或者灰度图像使用边缘检测算子得到,如拉普拉斯算子等;本文方法图像边缘图对彩色图像使用Cervenka彩色边缘算子得到,进而计算∇f[13]。对于具有真彩色信息的遥感影像,由于计算梯度时直接利用了彩色信息,避免了彩色图像转换为灰度图像时可能的边缘损失,因此采用该方法计算获得的GVF场能更真实地反映彩色影像的梯度场,更好地指引蛇模型收敛于影像的真实边缘。
本文采用的基于相关系数法的Cervenka彩色边缘提取算子对彩色边缘敏感,在遥感影像上能得到非常好的效果,且能处理三波段或者更高波段的影像。它由Cervenka[14]在1987年提出,邻域大小2像素×2像素×n,其中2像素×2像素邻域与Roberts梯度算子邻域相似。设 (i,j)代表同一坐标(i,j)下所有n个光谱分量图像像素亮度的算术平均值,fr是第r个光谱分量的亮度。像素(i,j)处的边缘检测算子的结果由式(6)的最小值给出:
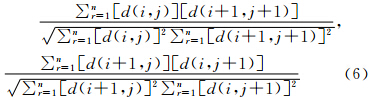
式中,d(k,l)=fr(k,l)- (k,l)。此边缘检测算子的设计原理实际为求相邻像素三波段像素值的相关系数,在2像素×2像素的区域中,将相关系数小的作为边缘的检测结果,值越小,为边缘的可能性越大。
本文提出的改进GVF 蛇模型水域矢量边界更新方法流程图如图 1所示。

|
| 图 1 改进的GVF蛇模型水域矢量边界更新流程 Fig. 1 The Flowchart of Water Vector Edge Updating of Improved GVF Snakes |
1) 依据水域矢量数据,通过矢量数据与影像数据地理位置信息,在遥感图像上初始化水域矢量边界初始位置。
2) 依据水域矢量边界数据,提取影像上对应矢量边界矩形区域影像,对其求取Cervenka彩色边缘图。
3) 使用Cervenka彩色边缘图求式(5)中水平与垂直梯度fx与fy,使用前向欧拉法求解式(5),求取梯度向量流场。
4) 使用GVF 蛇模型对初始水域边界进行变形演化,最终演化收敛曲线即为精确的水域矢量边界轮廓。
3 实验结果与分析
为了验证本文方法的效果,本文进行了大量实验。实验中,使用C++编写了相应算法。实验环境为Inter(R) Core i3,CPU 3.07 GHz,6.00 GB内存,Windows 7.0操作系统。本文给出了其中两组数据的实验情况,数据一为城市湖泊数据,影像数据大小为972 像素×988 像素,数据二为山区湖泊数据,影像数据大小1 163 像素×1 117 像素。其中实验数据的影像数据为2012年WorldView卫星拍摄的2.5 m分辨率三波段真彩色数据,格式为ErdasIMG;边界矢量数据为2010年人工矢量化的边界矢量图,格式为Shapefile。
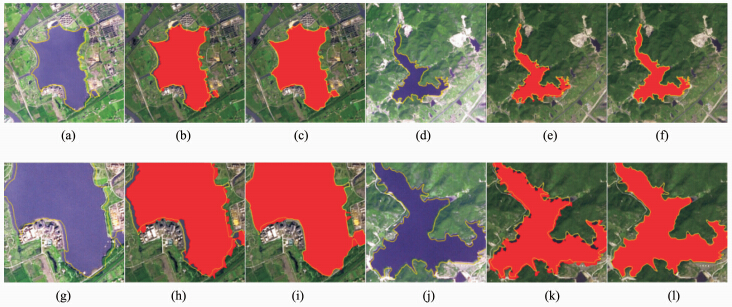
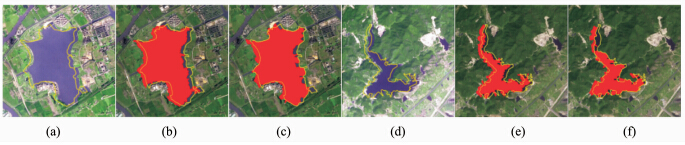
为了进一步验证本文方法的稳定性,实验中还将初始矢量数据分别向右、向左进行水平移动,每隔5个像素做一组实验,最远向右或向左水平移动30个像素,每组数据共进行了13组实验,并与Xu[11, 12]提出的原有传统GVF蛇模型进行了对比实验。图 2与图 3分别为初始边界整体水平右移15个像素与初始边界整体水平左移30个像素的实验结果图。在图 2与图 3中,图(a)、(d)分别为数据一与数据二初始边界与原图叠加效果图,图(b)、(e)分别为数据一与数据二传统GVF蛇模型提取边界所包含区域(红色区域)与人工提取真实边界(黄色细线)叠加效果图,图(c)、(f)分别为数据一与数据二改进GVF蛇模型提取边界所包含区域(红色区域)与人工提取真实边界(黄色细线)叠加效果图。图 2(g)~2(l)为图 2(a)~2(f)中黑色虚线框范围局部放大图。
|
| 图 2 传统与改进GVF蛇模型结果对比图(右移15像素) Fig. 2 The Updating Results of the GVF Snakes and the Improved GVF Snakes Model(15 Pixels to Right) |
|
| 图 3 传统与改进GVF蛇模型结果对比图(左移30像素) Fig. 3 The Updating Results of the GVF Snakes and the Improved GVF Snakes Model (30 Pixels to Left) |
为了进一步验证,将本文方法与四元数法和数学形态学法进行对比实验。由于本文方法使用已有水域矢量边界数据作为GVF蛇模型的初始位置,通过蛇模型演化实现水域提取,不能直接与四元数法和数学形态学法进行比较。为了和本文方法在同等条件下进行比较,使用四元数和形态学方法求取梯度,然后结合GVF 蛇模型进行水域提取,保证其流程与本文方法的一致性。对于四元数算法,本文选择了基于四元数旋转的方法[15];对于数学形态学方法,本文选择了基于马氏距离的形态学方法[16],其中数学形态学方法中,结构元素选择了边长为3的方形模板。
为了进一步从定量的角度对本文方法进行评价,采用定位准确度作为精度评价指标,将定位准确度计算中的错提像元个数、漏提像元个数、正确提取像元个数、实际像元个数、错提率以及漏提率都列出来,以便更详细地描述定位准确度。其中错提率、漏提率以及定位准确度定义如式(7)。并与传统GVF 蛇模型算法、四元数算法以及数学形态学算法进行了对比。同时,还对比了4种算法的耗时情况。
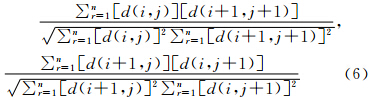
本文算法与传统GVF 蛇模型算法、四元数算法以及数学形态学算法的定量对比实验结果如表 1(由于篇幅原因只列出了数据一的结果,且表格中只列举了每平移10个像素的实验结果),其中平移距离正负数分别表示水平右移与左移;精度评价中所需的参考真实矢量边界信息是采取人工数字化水域矢量边界方式获得的,数字化结果见图 2(b)、2(c)、2(e)、2(f)、2(h)、2(i)、2(k)与图 2(l)中的黄色细线。
| 平移距离(像素) | 方法 | 错提像元个数 | 漏提像元个数 | 正确提取像元个数 | 实际像元个数 | 漏提率/(%) | 错提率/(%) | 时间/s | 定位准确度/(%) |
| 0 | 原有 | 8 885 | 2 481 | 208 137 | 210 618 | 4.22 | 1.18 | 67.82 | 94.60 |
| 四元数 | 5 043 | 2 167 | 208 451 | 210 618 | 2.39 | 1.03 | 77.95 | 96.58 | |
| 形态学 | 2 785 | 2 520 | 208 098 | 210 618 | 1.32 | 1.20 | 72.59 | 97.48 | |
| 本文 | 2 887 | 2 294 | 208 324 | 210 618 | 1.37 | 1.09 | 68.73 | 97.54 | |
| -10 | 原有 | 11 459 | 11 791 | 198 827 | 210 618 | 5.44 | 5.60 | 65.27 | 88.96 |
| 四元数 | 8 353 | 1 708 | 208 910 | 210 618 | 3.97 | 0.81 | 77.86 | 95.22 | |
| 形态学 | 4 084 | 2 558 | 208 060 | 210 618 | 1.94 | 1.21 | 72.28 | 96.85 | |
| 本文 | 4 279 | 2 267 | 208 351 | 210 618 | 2.03 | 1.08 | 68.47 | 96.89 | |
| -20 | 原有 | 19 673 | 18 452 | 192 166 | 210 618 | 9.34 | 8.76 | 66.74 | 81.90 |
| 四元数 | 18 861 | 3 870 | 206 748 | 210 618 | 8.96 | 1.84 | 77.56 | 89.21 | |
| 形态学 | 10 498 | 7 222 | 203 396 | 210 618 | 4.98 | 3.43 | 71.9 | 91.59 | |
| 本文 | 11 842 | 2 831 | 207 787 | 210 618 | 5.62 | 1.34 | 68.39 | 93.03 | |
| -30 | 原有 | 25 867 | 26 006 | 184 612 | 210 618 | 12.28 | 12.35 | 65.57 | 75.37 |
| 四元数 | 26 821 | 18 531 | 192 087 | 210 618 | 12.73 | 8.80 | 78.22 | 78.47 | |
| 形态学 | 19 616 | 19 213 | 191 405 | 210 618 | 9.31 | 9.12 | 72.27 | 81.56 | |
| 本文 | 18 407 | 15 116 | 195 502 | 210 618 | 8.74 | 7.18 | 69.01 | 84.08 | |
| 10 | 原有 | 6 801 | 11 752 | 198 866 | 210 618 | 3.23 | 5.58 | 66.00 | 91.91 |
| 四元数 | 6 311 | 1 760 | 208 858 | 210 618 | 3.00 | 0.84 | 78.36 | 96.17 | |
| 形态学 | 2 997 | 2 886 | 207 732 | 210 618 | 1.23 | 1.37 | 72.13 | 97.21 | |
| 本文 | 3 229 | 2 353 | 208 265 | 210 618 | 1.53 | 1.12 | 69.31 | 97.35 | |
| 20 | 原有 | 15 787 | 16 909 | 193 709 | 210 618 | 7.50 | 8.03 | 66.60 | 84.48 |
| 四元数 | 13 501 | 3 892 | 206 726 | 210 618 | 6.41 | 1.85 | 79.16 | 91.74 | |
| 形态学 | 10 640 | 6 052 | 204 566 | 210 618 | 5.05 | 2.87 | 72.48 | 92.07 | |
| 本文 | 10 200 | 3 189 | 207 429 | 210 618 | 4.84 | 1.51 | 68.02 | 93.64 | |
| 30 | 原有 | 23 819 | 23 752 | 186 866 | 210 618 | 11.31 | 11.28 | 66.94 | 77.41 |
| 四元数 | 22 619 | 15 434 | 195 184 | 210 618 | 10.74 | 7.33 | 76.74 | 81.93 | |
| 形态学 | 21 594 | 13 571 | 197 047 | 210 618 | 10.25 | 6.44 | 72.2 | 83.30 | |
| 本文 | 21 252 | 10 987 | 199 631 | 210 618 | 10.09 | 5.22 | 68.56 | 84.69 |
图 4为表 1定位准确度的图形化表示,图 4(a)为数据一对比图,图 4(b)为数据二对比图,图中黑色、红色、蓝色以及绿色曲线分别表示原有、本文改进、四元数以及数学形态学方法曲线。

|
| 图 4 四种算法定位准确度对比图 Fig. 4 The Location Accuracy Results of the Four Methods |
表 1表明,在算法效率方面,本文方法比原有方法耗时稍长,比四元数法与数学形态学法耗时要短。两组数据26组对比实验表明,本文方法比传统方法平均耗时约长2.90%,主要是由于Cervenka彩色边缘的求取计算量比较大。四元数法比本文方法耗时约长11.52%,主要是由于四元数法需要进行双次卷积运算。数学形态学法比本文方法耗时约长4.09%,主要是由于数学形态学法需要求取方差与协方差矩阵,并且求其逆矩阵。
图 4、表 1表明,当初始边界距真实边界距离增加时,原有方法与改进方法定位准确度都会下降。对于原有方法,当初始边界距真实边界大于15像素时,定位准确度平均下降至77.63%;对于改进方法,当初始边界距真实边界大于25像素时,其定位准确度平均下降至78.20%。显然,此时两种方法得到的结果都不能满足矢量更新的要求。但是相比原有方法,本文算法能得到更好的定位准确度,平均比原有方法高9.05%,特别是在左右偏离25个像素范围内,原有方法随着偏离距离增加,精度下降迅速,平均降低至66.90%,而本文改进算法由于采用彩色边缘图计算梯度向量流场,能更好地反映影像中地物的实际边缘梯度,平均定位准确度还能达到86.30%,这也说明本文方法更稳健,在一定范围内对初始边界不敏感。本文算法在定位准确度上比四元数法精度高2.10%,在处理效率上比其快11.52%。对于数学形态学法,本文算法在定位准确度上虽然只比其精度高0.95%,但在处理效率上比其快4.09%,而且对于形态学法,其定位准确度与处理效率都取决于结构元素与矢量排序算法的选择,具有比较大的不确定性。
图 4、表 1表明,初始边界偏离真实边界较远时,由于蛇模型方法存在局部收敛性的限制,本文方法效果虽然优于传统方法,但也不理想。通过实验分析,本文方法适用于初始边界偏离真实边界20个像素以内的情况。当初始边界偏离真实边界较远时,在实际应用中,对于地理坐标不匹配造成的平移,可以考虑在算法中增加用户可以指定的初始化平移参数来减小初始边界偏离真实边界的距离;对于初始边界偏离真实边界没有整体偏移规律或者缺少初始矢量边界数据的应用,可以考虑人工初始化边界。由于本文算法有大约20个像素的适应性,其初始化工作比传统的人工数字化有很大优势,因此可在保证精度的前提下,大量节省工作量。
对于上文中初始边界偏离真实边界较远的两种情况,分别使用原有方法与本文方法进行实验,其精度与效率评价结果如表 2所示。其中,数据一初始边界为原矢量数据整体右移50个像素后再下移40个像素的边界;数据二初始边界则为原矢量数据整体左移45个像素后再上移65个像素的结果。
表 2表明,当初始边界偏离真实边界较大时,在实际应用中,对于由地理坐标不匹配造成的平移,可以通过在算法中增加用户可以指定的初始化平移参数来减小初始边界偏离真实边界的距离。与原有GVF蛇模型算法相比,本文算法在牺牲不到2%效率的基础上,精度比原有方法平均提高了18.86%;对于初始边界偏离真实边界没有整体偏移规律或者缺少初始矢量边界数据的应用,通过人工进行初始边界的初始化。由于本文算法有大约20个像素的适应性,其初始化工作与传统的人工数字化相比具有更高的效率,且能达到较高的精度。与原有GVF蛇模型算法相比,本文算法在牺牲不到2%效率的基础上,精度比原有方法平均提高5.86%。综上所述,相比原有GVF蛇模型方法,在牺牲不到3%处理效率的基础上,本文方法在定位准确度与搜索范围上有较大优势;相比四元数与数学形态学法,本文方法在定位准确度上有一定优势,在处理效率上有较大优势,且本文方法在求取梯度图时不需要做参数选择,具备更好的适应性。
| 数据 | 偏离情况 | 方法 | 错提像元个数 | 漏提像元个数 | 正确提取像元个数 | 实际像元个数 | 漏提率/(%) | 错提率/(%) | 时间/s | 定位准确度/(%) |
| 数据一 | 右移50像素,下移40像素 | 原有 | 797 | 29 667 | 180 951 | 210 618 | 0.38 | 14.09 | 66.63 | 85.54 |
| 本文 | 2 642 | 3 118 | 207 500 | 210 618 | 1.25 | 1.48 | 67.79 | 97.27 | ||
| 无规律像素,人工初始化像素 | 原有 | 8 574 | 3 697 | 206 921 | 210 618 | 4.07 | 1.76 | 65.68 | 94.17 | |
| 本文 | 2 960 | 2 238 | 208 380 | 210 618 | 1.41 | 1.06 | 67.33 | 97.53 | ||
| 数据二 | 左移45像素,上移65像素 | 原有 | 3 090 | 24 901 | 86 488 | 111 389 | 2.77 | 22.35 | 162.45 | 74.87 |
| 本文 | 3 214 | 4 138 | 107 251 | 111 389 | 2.89 | 3.71 | 165.53 | 93.40 | ||
| 无规律,人工初始化 | 原有 | 12 621 | 1 919 | 109 470 | 111 389 | 11.33 | 1.72 | 161.16 | 86.95 | |
| 本文 | 3 334 | 3 111 | 108 278 | 111 389 | 2.99 | 2.79 | 163.46 | 94.21 |
本文由彩色边缘出发,对传统GVF蛇模型中梯度向量流场的生成进行改进,提出了一种改进基于彩色边缘的GVF蛇模型算法,并将其应用到基于遥感真彩色影像的水域矢量边界更新中。该方法将已有水域矢量边界数据作为GVF蛇模型初始位置,通过轮廓演化实现水域矢量边界更新。与原有方法对比试验表明,对于初始边界距真实边界不同距离情况,由于本文方法充分利用了真彩色遥感影像的梯度信息,相比传统GVF蛇模型具有更好精度,且在初始边界距真实边界一定范围内,对初始边界位置不敏感,可以完成水域矢量边界的更新任务。与四元数及数学形态学方法对比实验表明,本文方法在定位准确度与处理效率上有一定优势,且在求取梯度图时不需要进行参数选择。
由于蛇模型方法存在局部收敛性,在初始边界偏离真实边界较远时,本文方法虽然比传统方法要好,但结果也不理想。通过实验分析,本文方法适用于初始边界偏离真实边界20个像素以内的情况。下一步需要研究如何克服蛇模型的局部收敛性限制,进一步提高蛇模型搜索范围。
| [1] | Fan Dazhao, Zhang Yongsheng, Lei Rong, et al. Research on Automatic Updating of GIS Data[J].Science of Surveying and Mapping, 2005, 30(3):15-18 (范大昭, 张永生, 雷蓉, 等. GIS数据自动更新技术的研究[J]. 测绘科学, 2005, 30(3):15-18) |
| [2] | Zhang Xiaodong, Li Deren, Gong Jianya, et al. A Change Detection Method of Integrating Remote Sensing and GIS[J]. Geomatics and Information Science of Wuhan University, 2006, 31(3):265-269(张晓东, 李德仁, 龚健雅, 等. 遥感影像与GIS分析相结合的变化检测方法[J]. 武汉大学学报· 信息科学版, 2006, 31(3):265-269) |
| [3] | Zhang Jianqing, Dong Ming, Zhang Hongwei. Automatically Registration of TM Image and GIS Vector Data[J]. Geomatics and Information Science of Wuhan University, 2005, 30(11):950-954(张剑清, 董明, 张宏伟. TM影像与GIS矢量数据的自动配准[J]. 武汉大学学报· 信息科学版, 2005, 30(11):950-954) |
| [4] | Bonnefon R, Dherete P, Desachy J. Geographic Information System Updating Using Remote Sensing Images[J]. Pattern Recognition Letters, 2002, 23(9):1 073-1 083 |
| [5] | Mena J B. State of the Art on Automatic Road Extraction for GIS Update:A Novel Classification[J]. Pattern Recognition Letters, 2003, 24(16):3 037-3 058 |
| [6] | Kass M, Witkin A, Terzopoulos D. Snakes:Active Contour Models[J]. International Journal of Computer Vision, 1988, 1(4):321-331 |
| [7] | Fortier M A, Ziou D, Armenakis C, et al. Automated Correction and Updating of Road Databases from High-resolution Imagery[J]. Canadian Journal of Remote Sensing, 2001, 27(1):168-174 |
| [8] | Han Min, Sun Yang. A Method of Vector Edge Updating Based on Grouping Snake Model in GIS[J].Acta Geodaetica et Cartographica Sinica, 2009, 38(2):168-174(韩敏, 孙杨. 一种基于分组式蛇模型的GIS矢量边界更新方法[J]. 测绘学报, 2009, 38(2):168-174) |
| [9] | Tang Wei, Zhao Shuhe. Road Extraction in Quaternion Space from High Spatial Resolution Remorely Sensed Images Basing on GVF Snake Model[J]. Journal of Remote Sensing, 2011, 15(5):1 041-1 052(唐伟, 赵书河. 基于GVF和Snake模型的高分辨率遥感图像四元数空间道路提取 [J]. 遥感学报, 2011, 15(5):1 041-1 052) |
| [10] | Zhou Yi, Tang Guoan, Xi Yu, et al. A Shoulder-lines Connection Algorithm Using Improved Snake Model[J]. Geomatics and Information Science of Wuhan University, 2013, 28(1):82-85(周毅, 汤国安, 习羽, 等. 引入改进蛇模型的黄土地形沟沿线连接算法[J]. 武汉大学学报· 信息科学版, 2013, 28(1):82-85) |
| [11] | Xu C, Prince J L. Gradient Vector Flow:A New External Force for Snakes[C]. IEEE Computer Society Conference, San Juan, Argentina, 1997 |
| [12] | Xu C, Prince J L. Prince. Snakes, Shapes, and Gradient Vector Flow[J]. Image Processing IEEE Transactions on, 1998, 7(3):359-369 |
| [13] | Yang L, Meer P, Foran D J. Unsupervised Segmentation Based on Robust Estimation and Color Active Contour Models[J]. Information Technology in Biomedicine, IEEE Transactions on, 2005, 9(3):475-486 |
| [14] | Cervenka V, Charvat K. Survey of the Image Processing Research Applicable to the Thematic Mapping Based on Aerocosmic Data[C]. Technical Report, Geodetic and Carthographic Institute, Prague, Czechoslovakia, 1987 |
| [15] | Sangwine S J. Colour Image Edge Detector Based on Quaternion Convolution [J]. Electronics Letters, 1998, 34(10):969-971 |
| [16] | Al-Otum H M. Morphological Operators for Color Image Processing Based on Mahalanobis Distance Measure[J].Optical Engineering, 2003, 42(9):2 595-2 606 |
 2015, Vol. 40
2015, Vol. 40



