文章信息
- 岳林蔚, 沈焕锋, 袁强强, 张良培, 兰霞
- YUE Linwei, SHEN Huanfeng, YUAN Qiangqiang, ZHANG Liangpei, LAN Xia
- 基于双边结构张量的局部自适应图像超分辨率重建
- A Bilateral Structure Based Local Adaptive Regularization for Super-resolution
- 武汉大学学报·信息科学版, 2015, 40(4): 493-497
- Geomatics and Information Science of Wuhan University, 2015, 40(4): 493-497
- http://dx.doi.org/10.13203/j.whugis20130324
-
文章历史
- 收稿日期:2013-07-13
2. 武汉大学资源与环境科学学院, 湖北 武汉, 430079;
3. 武汉大学测绘学院, 湖北 武汉, 430079;
4. 武汉大学数学与统计学院, 湖北 武汉, 430079
2. School of Resource and Environmental Science, Wuhan University, Wuhan 430079, China;
3. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China;
4. School of Mathmatics and Statistics, Wuhan University, Wuhan 430079, China
图像超分辨率重建技术通过对多幅具有互补信息的低分辨率观测图像进行处理,获得一幅或多幅较高分辨率的图像[1]。近年来,对超分辨率重建“软件”算法的研究越来越受到关注,已成为图像处理领域最活跃的研究方向之一[2]。
由于空间域超分辨率重建方法具有诸多优势,目前,国内外学者已经发展了多个空域处理的框架,主要包括非均匀内插[3]、凸集投影(POCS)[4]、迭代反投影[5]、最大似然估计(ML)[6]、最大后验概率估计(MAP)[7]等。在这些研究框架中,MAP方法由于理论支持严谨,有较强的融入空间先验约束的能力,可将病态问题转化成有唯一解的代价函数最优化问题,应用最为广泛。国内外学者基于MAP框架发展了多种图像超分辨率重建方法,广泛应用在遥感[8]、导航[9]和医学图像[10]处理等多个领域。
在MAP框架中,先验模型对图像重建具有重要的影响[11]。拉普拉斯[12]、高斯-马尔柯夫先验模型[13]等L2范数先验主要对图像施加平滑约束,易产生图像过平滑的现象;而以总变差(TV)先验[14]和双边总变差(BTV)先验[15]为代表的L1范数先验则更侧重边缘的保持,但噪声较强时会在平滑区域形成阶梯效应。近年来发展的混合范数先验结合L1和L2范数的优势和不足,利用影像局部空间信息对不同区域采用不同的范数进行处理,取得了较好的效果。Huber-Markov先验模型[16]是一种分段的混合范数先验模型,可以对平滑区域和边缘区域进行不同的处理,在去除噪声的同时保护图像的边缘信息。然而,Huber-Markov模型在噪声较强的情况下依然缺乏稳健性;并且,由于Huber模型属于典型的混合范数问题,其非线性特征使得模型的求解效率不高。
本文引入双边结构张量对先验函数进行L1范数与L2范数的分段,构建一种局部自适应的先验模型,有效提高了重建模型的稳健性;同时,引入迭代重加权的思想,将模型的混合范数先验转换到L2范数,基于预条件共轭梯度方法进行图像的快速、精确求解。
1 基于MAP的局部自适应超分辨率重建框架 1.1 重建模型
超分辨率图像重建是一个典型的逆问题,可以将低分辨率影像的形成过程理解为将高分辨率图像通过包括几何运动、光学模糊、亚采样及附加噪声的降质过程,得到如下模型:
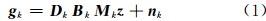
式中,z 表示所求的高分辨率图像;g k表示用于重建的某一幅低分辨率图像(k为图像编号);Mk、Bk、 D k和 n k分别表示几何运动矩阵、模糊矩阵、亚采样矩阵和附加噪声。由模型(1)可以看出,超分辨率重建模型的求解就是已知降质后图像,尽可能重建出高分辨率图像的过程,是一个大型的病态逆问题[17]。这样的欠定问题很难直接进行精确求解,需要借助先验知识,采用有效的正则化约束来稳定求解的过程,MAP是一个广泛应用的求解框架。
令 W k= D k B k M k,通过贝叶斯原理可以得到一般的MAP代价函数:
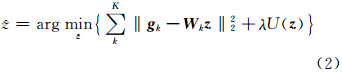
式(2)主要由三个部分组成:第一项为数据一致性约束项,描述模型误差;第二项U( z )表示的是先验项,决定求解的稳定性和唯一性;而正则化参数λ用来控制两项之间的平衡关系。
1.2 基于双边结构张量的局部自适应先验
Huber-Markov模型采用4个方向上的梯度信息作为图像同质和异质区域的分段标准。但是在噪声较强的情况下,方向梯度在同质区域内对噪声非常敏感,稳定性较差。本文引入一种较为稳健的判别测度——双边结构张量[18],并联合传统模型中4个方向的二阶梯度算子进行图像平滑和边缘区域的判别,从而构建局部自适应的先验模型。
双边结构张量同时考虑像素周围梯度信息和像素之间的欧几里德距离关系。首先利用水平和垂直两个方向的梯度信息,对一定窗口大小内的每一个像素,构造结构张量矩阵:

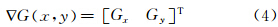
双边结构张量结合了空间距离式(5)和梯度距离式(6),对结构张量矩阵进行加权,能够更准确地排除噪声的影响,用来衡量图像局部的平滑程度[18]:

式中,dsi表示窗口w内像素(xi,yi)和中心像素(xo,yo)的欧几里德距离;dgi表示像素之间水平、垂直两个梯度方向的距离。可以定义权值系数:

这里的系数Q用来归一化权值,表示为:

因此,双边结构张量矩阵可以定义为:
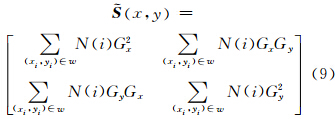
双边结构张量同时考虑图像局部块的空间距离和梯度距离的信息,相比单方向梯度作为判别标准更为稳健。本文中采用的分段方式是采用双边结构张量和4个方向平滑测度联合判别的方法,可以将先验项表示为:

式中,dtc( z )表示像素周围4个方向的二阶梯度。C为一个集簇(本文中取中心像素周围3×3的邻域系统,而C为图像上集簇的集合)。 这里的Lp范数不再单一取决于4个方向上的梯度。当像素双边结构张量值以及方向梯度同时小于阈值时,则视为平滑区域,用L2范数处理;而其余区域用L1范数处理,保持细节信息。本文将决定每个像素集簇C的范数p的函数定义为:
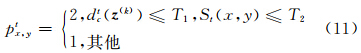
通过这种方式,将双边结构张量信息和4个方向的梯度信息结合起来,共同参与图像局部自适应处理的过程,从而增强在噪声情况下先验项重建的鲁棒性。结合局部自适应先验,所要求解的最小化能量函数可以表示成:

快速、稳定的数值求解方法对于重建模型十分关键[15]。迭代重加权范数(iteratively reweighted norm,IRN)算法的主要思想是通过选取合适的权系数矩阵,将不定范数问题转换为等价的L2范数问题,这样可以通过常规求解方法来优化目标泛函。经过证明,迭代加权变换后的方程解最终收敛于代价函数的极小解[19]。本文的先验模型可以构造权系数矩阵进行线性化:
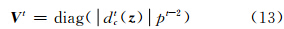
式中,p由阈值T1和T2决定,即模型的能量函数转换为:

至此,本文所求解的问题变为求常规L2范数的最小化最优解。对这个能量函数进行最小化求解时,需要求得其拉格朗日方程,然后优化求解:

式中,L z表示先验项求导之后的线性系数矩阵。本文采用基于带状近似逆条件( FBIP)的预条件共轭梯度法对模型进行求解[14]。
2 实 验
本文主要通过两组实验验证算法的有效性。采用的图像是Cameraman(大小为200 像素×200 像素)和Lena(大小为256像素×256像素),分别对图像添加不同程度的噪声和模糊,经过降质可得到4幅具有亚像元位移的模拟图像。
4幅图像采用的亚像元位移分别为(0,0)、(0,0.5)、(0.5,0)、(0.5,0.5),在下述各种模型中均仅考虑全局运动模型,降采样因子设为2。 在实验中,我们采用峰值信噪比(peak signal to noise ratio,PSNR)、相关系数(correlation coefficient,CC)和结构相似性指数(structure similarity image measure,SSIM)作为重建图像的评价标准。通常,PSNR、CC和SSIM的值越大,表示重建结果越理想。 2.1 实验结果的精度评价
首先对Cameraman图像(图 1(a))降采样,然后分别对图像添加均值为0,方差为0.001~0.005(归一化后)的高斯噪声,得到5组低分辨率图像序列。然后用本文算法对其进行超分辨率重建,同时将其与拉普拉斯先验和Huber-Markov先验以及双边总变差先验(BTV)处理的结果进行对比分析。

|
| 图 1 原始高分辨率图像 Fig. 1 The Original High Resolution Images |
表 1给出了部分实验具体的评价指标结果,图 2给出了视觉效果比较,图 3描述了几种方法定量评价指标的变化趋势。通过实验结果可以看出,拉普拉斯先验在保证细节信息的前提下,在图像的平滑区域残留了大量噪声;传统的HMRF模型能够在去除噪声的基础上保持边缘细节,但对噪声较为敏感,会产生分段判别的误差,导致平滑区域噪声残留;BTV先验具有较好的抑制噪声和保持图像边缘的能力,但在有噪声时会在平滑区域产生边缘效应,从而影响重建结果;本文方法能够在边缘保持和噪声去除两者之间达到较好的平衡效果,定量指标在各种噪声情形下都有稳定的提高。
| 噪声方差 | 评价指标 | 拉普拉斯先验 | HMRF先验 | BTV先验 | 本文方法 |
| SSIM | 0.729 | 0.860 | 0.881 | 0.906 | |
| 0.001 | PSNR | 26.837 | 28.486 | 28.790 | 29.047 |
| CC | 0.993 5 | 0.995 6 | 0.995 8 | 0.996 0 |

|
| 图 2 0.001高斯噪声情况下重建结果 Fig. 2 Reconstruction Results for Cameraman with Gaussian Noise (0.001) |

|
| 图 3 不同噪声情况下Cameraman重建结果比较 Fig. 3 Comparison for Reconstruction Results for Cameraman Under Different Noise Case |
第二组实验采用纹理更加丰富的Lena图像,按照相似的处理方式得到降质之后的序列图像,并添加方差为0.001和0.005的高斯噪声。由于模拟实验中PSF的大小通常视为已知,因此,在这组实验中加入大小为3像素×3像素,方差为1的高斯模糊。表 2给出了几种方法的定量评价结果。实验证明,考虑模糊的情形下,先验函数依然有效。
| 噪声方差 | 评价指标 | 拉普拉斯先验 | HMRF先验 | BTV先验 | 本文方法 |
| SSIM | 0.779 | 0.821 | 0.821 | 0.838 | |
| 0.001 | PSNR | 28.073 | 28.552 | 28.660 | 28.831 |
| CC | 0.977 9 | 0.980 0 | 0.980 5 | 0.981 3 | |
| SSIM | 0.709 | 0.739 | 0.761 | 0.780 | |
| 0.005 | PSNR | 26.313 | 26.682 | 26.905 | 27.137 |
| CC | 0.966 3 | 0.966 1 | 0.970 7 | 0.972 2 |
为了验证求解算法的效率,将本文提出的快速求解算法与传统手动调试步长的梯度下降法进行了比较。主要通过评价指标PSNR和相对残差的变化情况,比较算法的收敛时间和迭代次数,验证迭代重加权求解的精度和速度。
本文选取了Cameraman序列影像中噪声方差为0.001的一组实验,通过比较Huber-Markov模型用最速下降梯度法直接求解,以及迭代重加权范数结合预条件共轭梯度法求解这两种情况的收敛速度,来验证本文优化算法的求解优势。在这里,采用相对残差 dt=‖∇E(zn)‖/‖∇E(z0)‖来作为判别收敛的残差。
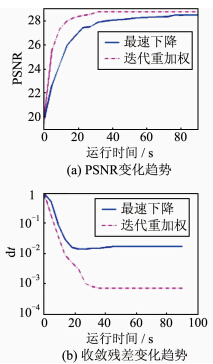
表 3和图 4显示了Huber-Markov模型在两种优化算法下的求解情况,迭代收敛条件为:当迭代次数大于100次,或相对梯度范数dt小于迭代收敛残差10-4时,迭代视为收敛。
| 优化算法 | PSNR | 迭代收敛次数 | 求解时间/s |
| 最速下降 | 28.486 | 100 | 88.6 |
| 迭代重加权 | 28.750 | 25 | 28.8 |
|
| 图 4 两种求解方法的收敛情况比较 Fig. 4 Comparison for Convergence Performance of the Two Methods |
从实验结果可以看出,经过迭代重加权范数转换后的线性优化策略比传统的优化方法在迭代次数和求解时间上有大幅提高,并且能够获得更加准确的最优化解。
3 结 语
本文引入双边结构张量对图像进行细节信息的评估,与方向梯度测度联合分段建立了图像超分辨率重建的先验模型,并采用了迭代重加权范数的思想应用于非线性混合范数问题的求解。实验证明,本文提出的基于双边结构张量的局部自适应先验能够提高重建精度,特别是在噪声情况下更加稳健,可以在抑制平滑区域噪声的同时,有效保持图像的边缘信息;另外,迭代重加权方法不但可以提高超分辨率重建模型中混合范数问题的求解速度,而且可以使求解更加稳定和精确。
| [1] | Tan Bing, Xu Qing, Geng Zexun, et al. A Survey of Super Resolution for Image Reconstruction[J]. Journal of Information Engineering University, 2003, 4:93-97 (谭兵, 徐青, 耿则勋, 等. 超分辨率图象重建技术发展现状 [J]. 信息工程大学学报, 2003, 4:93-97) |
| [2] | Cossairt O, Gupta M, Nayar S K. When Does Computational Imaging Improve Performance?[J]. IEEE Transactions on Image Processing, 2013, 22(2):447-458 |
| [3] | Shah N R, Zakhor A. Resolution Enhancement of Color Video Sequences[J]. IEEE Transactions on Image Processing, 1999, 8(6):879-885 |
| [4] | Zhang Y, Zhou Q. An Improved Method for POCS Superresolution Image Reconstruction[C]. 2011 International Conference on Electronics, Communications and Control, Ningbo, China, 2011 |
| [5] | Irani M, Peleg S. Improving Resolution by Image Registration[J]. Graphical Models and Image Processing, 1991, 53(3):231-239 |
| [6] | Schultz R R, Stevenson R L. Extraction of High-resolution Frames from Video Sequences[J]. IEEE Transactions on Image Processing, 1996, 5(6):996-1 011 |
| [7] | Shen H F, Zhang L P, Huang B, et al. A Map Approach for Joint Motion Estimation, Segmentation, and Super Resolution[J]. IEEE Transactions on Image Processing, 2007, 16:479-490 |
| [8] | Shen H F, Du L J, Zhang L P, et al. A Blind Restoration Method for Remote Sensing Images[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(6):1 137-1 141 |
| [9] | Guo Lin, Chen Qinghu. Adaptive Super-resolution Reconstruction of Image Sequences with Structure Preserving[J]. Geomatics and Information Science of Wuhan University, 2011, 36(5):548-551 (郭琳, 陈庆虎.结构保持的图像序列自适应超分辨率重建[J]. 武汉大学学报·信息科学版, 2011, 36(5):548-551) |
| [10] | Liu H C, Li S T, Yin H T. Infrared Surveillance Image Super Resolution via Group Sparse Representation[J]. Optics Communications, 2013, 289:45-52 |
| [11] | Lefkimmiatis S, Ward J P, Unser M. Hessian Schatten-norm Regularization for Linear Inverse Problems[J]. IEEE Transactions on Image Processing, 2013, 22(5):1 873-1 888 |
| [12] | Shen D F, Chiu C W. Fundamental Techniques for Resolution Enhancement of Average Subsampled Images[J]. Journal of Electronic Imaging, 2012, 21(3):033027-1-033027-10 |
| [13] | Gleich D. Markov Random Field Models for Non-quadratic Regularization of Complex SAR Images[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2012, 5(3):952-961 |
| [14] | Ng M K, Shen H, Lam E Y, et al. A Total Variation Regularization Based Super-resolution Reconstruction Algorithm for Digital Video[J]. EURASIP Journal on Advances in Signal Processing, 2007:74 585 |
| [15] | Matakos A, Ramani S, Fessler J A. Accelerated Edge-preserving Image Restoration Without Boundary Artifacts[J]. IEEE Transactions on Image Processing, 2013, 22(5):2 019-2 029 |
| [16] | Pan R, Reeves S J. Efficient Huber-markov Edge-preserving Image Restoration[J]. IEEE Transactions on Image Processing, 2006, 15(12):3 728-3 735 |
| [17] | Yuan Xiaohua, Ouyang XiaoLi, Xia Deshen. An Overview on Super Resolution Image Restoration[J]. Geography and Geo-Information Science, 2006, 22(3):43-47(袁小华, 欧阳晓丽, 夏德深. 超分辨率图像恢复研究综述[J]. 地理与地理信息科学, 2006, 22(3):43-47) |
| [18] | Zhang L, Zhang D. A Multi-scale Bilateral Structure Tensor Based Corner Detector[J]. Computer Vision-Accv 2009, 2010:618-627 |
| [19] | Wohlberg B, Rodriguez P. AN l 1-TV Algorithm for Deconvolution with Salt and Pepper Noise[C]. IEEE International Conference on, Taipei, 2009 |
 2015, Vol. 40
2015, Vol. 40



