文章信息
- 徐涵秋, 林中立, 潘卫华
- XU Hanqiu, LIN Zhongli, PAN Weihua
- 单通道算法地表温度反演的若干问题讨论——以Landsat系列数据为例
- Some Issues in Land Surface Temperature Retrieval of Landsat Thermal Data with the Single-channel Algorithm
- 武汉大学学报·信息科学版, 2015, 40(4): 487-492
- Geomatics and Information Science of Wuhan University, 2015, 40(4): 487-492
- http://dx.doi.org/10.13203/j.whugis20130733
-
文章历史
- 收稿日期:2013-12-02
2. 福建省水土流失遥感监测评价重点实验室, 福建 福州, 350108;
3. 福建省气象科学研究所, 福建 福州, 350001
2. Fujian Provincial Key Laboratory of Remote Sensing of Soil Erosion, Fuzhou 350108, China;
3. Institute of Meteorological Science of Fujian Province, Fuzhou 350001, China
地表温度(land surface temperature)是区域热环境研究的重要参数[1],它的获取主要是依靠气象站实测和卫星热红外遥感手段。由于气象站获得的只是有限点的数据,对研究空间尺度热环境的意义十分有限,因此,获取大范围地表温度信息的唯一来源是遥感卫星的热红外数据。
在中尺度遥感数据中,Landsat系列卫星的热红外数据得到了广泛的应用,已有多种相应的地表温度反演算法[2, 3, 4],其中Jiménez-Muñoz和Sobrino开发的单通道算法(single channel method,SC)[3]由于所需大气校正参数少,得到了广泛应用。该算法最初提出时,只提供了针对TM热红外数据的大气参数,使得其后的许多基于ETM+数据的研究也只能采用TM的大气参数来计算地表温度。虽然Jiménez-Muñoz和Sobrino在2009年推出了该算法的改进版,增加了针对ETM+的大气参数,但许多研究者并未了解这一情况,仍然继续使用着2003年针对TM的大气参数。这一参数的混用究竟会产生多大的误差,迄今也无相关研究涉及。由于热红外影像反演的地表温度经常缺乏对应的实测地面温度,难以进行精度验证,因此,选择正确的公式和参数是保证反演精度的必要前提。本文基于实测地表温度数据,以Landsat系列卫星的热红外影像为例,对Jiménez-Muñoz和Sobrino SC反演的地表温度进行比较和验证,并特别就该算法对最新发射的Landsat 8 热红外数据的应用潜力进行了探索。 1 单通道算法 1.1 2003版单通道算法
SC算法由Jiménez-Muñoz和Sobrino于2003年提出[3],其公式为:
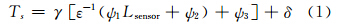
式中,γ和δ是基于Planck函数的两个参数,可由下式获得:
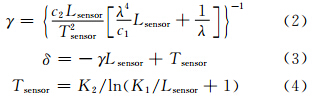
式中,Lsensor为辐射值(W/(m2·sr·μm));ε为地表比辐射率;Tsensor为传感器处亮温值(K);K1和K2为热红外波段的定标常数;λ为热红外波段的中心波长或有效波长;c1、c2是Planck辐射常数,分别为1.191 04×108 W·μm4/(m2·sr)和14 387.7 μm·K; ψ1、ψ2、ψ3是大气水汽含量w的函数,其计算公式为:
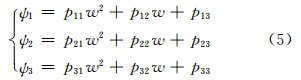
式中,pij (i,j= 1,2,3)是与水汽含量w相关的大气参数,对于TM 6波段,作者给出了特定参数,见表 1。
| λ/μm | K1/(W/(m2\5μm2\5sr)) | K2 /K | w/(g/cm2) | pij(i = 1,2,3, j = 1,2,3) | |||
| Landsat TM | 11.45 | 607.76 | 1 260.56 | ||||
| 2010-05-24 | 1.399 | 0.147 14 | -0.155 83 | 1.123 40 | |||
| -1.183 60 | -0.376 07 | -0.528 94 | |||||
| -0.045 54 | 1.871 90 | -0.390 71 | |||||
| Landsat ETM+ | 666.09 | 1 282.71 | |||||
| 2000-05-04 | 11.45 | 1.270 | 0.045 97 | 0.062 69 | 1.008 18 | ||
| -0.322 97 | -2.168 01 | 0.556 98 | |||||
| -0.063 97 | 1.693 24 | 0.457 47 | |||||
| 2001-05-23 | 11.269 | 2.564 | 0.045 97 | 0.062 69 | 1.008 18 | ||
| -0.322 97 | -2.168 01 | 0.556 98 | |||||
| -0.063 97 | 1.693 24 | 0.457 47 | |||||
| 2002-05-26 | 11.45 | 2.416 | 0.065 18 | 0.006 83 | 1.027 17 | ||
| -0.530 03 | -1.258 66 | 0.104 90 | |||||
| -0.019 65 | 1.369 47 | -0.243 10 | |||||
| Landsat-8 | |||||||
| 2013-08-04 | τ | L↑ | L↓ | ||||
| TIRS 10 | 10.90 | 774.89 | 1 321.08 | 4.180 | 0.449 38 | 4.120 81 | 6.137 73 |
| TIRS 11 | 12.01 | 480.89 | 1 201.14 | 0.311 57 | 4.867 53 | 6.748 09 | |
| 注:w、pij用于计算式(5),此处的pij选用的是每个时相获得最佳精度所使用的大气参数(参见表 2)。 | |||||||
如果使用有效波长λe计算式(2),其计算公式为:
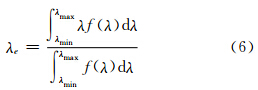
式中,f(λ)为热红外波段的光谱响应函数;λmax、λmin分别为波段光谱范围的最大和最小值。
1.2 2009版单通道算法
2009年,Jiménez-Muñoz和Sobrino对原算法提出了改进版[5],对大气参数和公式进行了两大修改。
1) 增加了5组针对ETM+ 6波段的大气参数,避免了ETM+ 6波段因采用 TM 6的大气参数而可能产生的误差。
2) 用式(7)~(9)取代式(2)~(4)来计算 γ、δ和Tsensor:
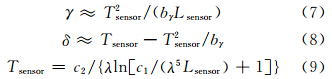
式中,TM的bγ为1 256, ETM+的bγ为1 277,式(9)用Planck函数取代式(4)来计算亮温。显然,2009版较之于2003版有较大的改变。
1.3 地表比辐射率ε的计算
由于本次地表温度反演采用的是Jiménez-Muñoz和Sobrino的SC算法,因此对于TM/ETM+影像,ε的计算同样采用他们提出的基于植被覆盖度的算法[6],以便与SC算法更好地匹配。
与之前的Landsat卫星不同的是,Landsat 8具有独立的热红外传感器TIRS,并有TIRS 10和TIRS 11两个波段。因此,可采用MODIS光谱库和Nichol的数据[7, 8]来确定ε。TIRS 10的比辐射率取值如下:植被0.981 6,土壤0.972 2,建筑物0.921 2,水体0.990 8;TIRS 11辐射率取值:取植被0.984 2,土壤0.976 3,建筑物0.933 7,水体0.990 2。 2 实 验
本研究选用福州市Landsat 5、7、8号星的热红外影像来进行实验,时间分别为2000-05-04、2001-05-23、2002-05-26、2010-10-24、2013-08-04 (后者下载于美国地质调查局(USGS)于2014-02-17重新定标处理的数据)。验证点的实测地表温度来自福州乌山国家基准气候站(26°4′39″N,119°17′24″E),大气水汽含量(w)取自美国宇航局提供的全球大气参数库(NCEP)[9]。表 1列出了利用SC算法计算地表温度所需的参数。
新的 Landsat 8 TIRS传感器有两个独立的热红外波段,可以通过劈窗算法来反演地表温度。但由于TIRS的定标参数尚不稳定,因此USGS暂不鼓励使用劈窗算法,仍建议采用TM的单波段方式来计算地表温度[10]。有鉴于此,本文尝试使用SC算法来计算Landsat 8的地表温度,以考察SC是否可以用于反演Landsat 8的地表温度。但是,由于本次实验影像的大气水汽含量较高(表 1),因此不用式(5)计算ψ1、ψ2、ψ3,而是用它们的原始推导公式来计算[5],即:
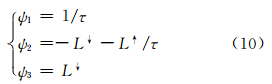
式中,τ为大气透过率;L↑和L↓ 为大气上行和下行辐射强度;通过MODTRAN软件来估算。根据实验区所处地理方位与季相,将中纬度夏季大气廓线作为MODTRAN大气剖面数据输入,并结合TIRS 10、11波段的光谱响应函数,在大气水汽含量1.0~4.2 g/cm2范围间模拟得到τ、L↑、L↓ ,列于表 1。 3 结果与讨论 3.1 精度验证
根据以上公式分别反演出各实验影像的地表温度,然后将其与福州国家基准气候站实测的地表温度进行比较。由表 2可知,在选择正确的参数和算法版本后,SC算法反演的地表温度具有很好的精度。以最佳精度计算,SC的平均误差只有-0.51 ℃,而绝对平均误差也只有1.2 ℃。
| 大气参数库 | 波长 λ /μm | 地表温度/℃ | 误差/℃ | ||
| 2000-05-04 | |||||
| 实测 | 31.94 | ||||
| ETM+ 6 | 2003版 | 11.45 | 32.46 | 0.52 | |
| 2009版 | SAFREE402 | 11.45 | 32.04 | 0.10 | |
| 2001-05-23 | |||||
| 实测 | 31.54 | ||||
| ETM+ 6 | 2003版 | 11.269 | 37.22 | 5.68 | |
| 2009版 | SAFREE402 | 11.269 | 33.16 | 1.62 | |
| 2002-05-26 | |||||
| 实测 | 39.65 | ||||
| ETM+ 6 | 2003版 | 11.45 | 40.59 | 0.94 | |
| 2009版 | TIGR1761 | 11.45 | 39.15 | -0.50 | |
| 2010-05-24 | |||||
| 实测 | 36.93 | ||||
| TM 6 | 2003版 | 11.45 | 35.90 | -1.03 | |
| 2009版 | TIGR1761 | 11.45 | 35.79 | -1.14 | |
| 2013-08-04 | |||||
| 实测 | 60.57 | ||||
| TIRS 10 | 2009版 | 57.80 | -2.77 | ||
| TIRS 11 | 2009版 | 64.20 | 3.63 | ||
| TIRS(10+11)/2 | 61.00 | 0.43 | |||
| 平均误差 | -0.51 | ||||
| 绝对平均误差 | 1.20 | ||||
| 注:平均误差是用各时相的最小误差值(以斜体表示)来计算均值;绝对平均误差是以各时相最小误差的绝对值来计算均值。 | |||||
表 2中ETM+数据采用2009版的算法和参数反演的地表温度的平均误差为0.41 ℃,绝对平均误差为0.74 ℃;而采用2003版的算法和参数反演的地表温度的平均误差和绝对平均误差都为2.38 ℃,明显大于2009版。可见2009年的新算法及其针对ETM+提出的大气参数显著地提高了地表温度的反演精度。而对于TM数据,2003版的精度只略高于2009版,这可能与当时主要针对TM开发的2003版算法已经有了很高的精度有关[3, 5]。 3.3 不同亮温计算公式的比较
2009版的算法推荐用Planck函数来计算亮温,但现有许多算法都用Landsat的亮温式(4)来计算。究竟基于二者计算出的地表温度是否有差别,本次研究也做了探讨。从表 3可以看出,Landsat亮温公式计算出的地表温度要比Planck函数计算的地表温度低约0.5℃;若与实测温度对比,Planck函数计算的地表温度的绝对平均误差为1.01 ℃,而Landsat亮温公式计算的绝对平均误差为1.12 ℃,二者差距为0.11 ℃。
| 亮温公式比较 | 波长λ比较 | 大气参数库比较 | |||||||
| 亮温公式 | 大气参数库 | 波长λ/μm | 误差/℃ | 波长λ/μm | 大气参数库 | 误差/℃ | 大气参数库 | 误差/℃ | |
| 2000-05-04 | 0.10 | SAFREE402 | |||||||
| ETM+6 | Planck | SAFREE402 | 11.45 | 0.10 | 11.269[5] | SAFREE402 | -0.71 | STD66 | 0.32 |
| Landsat | -0.42 | 11.335[9, 12, 13] | SAFREE402 | -0.19 | TIGR1761 | 0.36 | |||
| 11.450[10] | SAFREE402 | 0.10 | TIGR2311 | -0.10 | |||||
| TIGR61 | 0.23 | ||||||||
| 2001-05-23 | SAFREE402 | 2.44 | |||||||
| ETM+6 | Planck | SAFREE402 | 11.45 | 2.44 | 11.269[5] | SAFREE402 | 1.62 | STD66 | 3.76 |
| Landsat | 1.91 | 11.335[9, 12, 13] | SAFREE402 | 1.91 | TIGR1761 | 4.28 | |||
| 11.450[11] | SAFREE402 | 2.44 | TIGR2311 | 3.08 | |||||
| TIGR61 | 3.33 | ||||||||
| 2002-05-26 | SAFREE402 | -2.23 | |||||||
| ETM+6 | Planck | TIGR1761 | 11.45 | -0.50 | 11.269[5] | TIGR1761 | -1.37 | STD66 | -1.12 |
| Landsat | -1.02 | 11.335[9, 12, 13] | TIGR1761 | -1.06 | TIGR1761 | -0.50 | |||
| 11.450[11] | TIGR1761 | -0.50 | TIGR2311 | -1.79 | |||||
在实际计算中,不同研究者采用的λ值并不相同,有的采用中心波长,有的采用有效波长,因此有必要对由此产生的差别进行比较。表 3列出了比较有代表性的三组λ值及其根据2009版算法计算出的地表温度。其中,文献[5]采用有效波长值,文献[11]和[9, 12, 13]采用的是中心波长值。从表 3中可以看出,虽然Jiménez-Muñoz和Sobrino在文献[5]中提倡用有效波长值来计算地表温度,但其绝对平均误差却是最大的(1.23 ℃),而使用USGS的Landsat网站提供的中心波长11.45 μm [11]的绝对平均误差最小(1.01 ℃),其次是文献[9, 12, 13]采用的λ值(1.05 ℃)。由于地表温度随着λ值的增大而增大,对于ETM+ 6,最小的λ取值(11.296 μm)和最大的λ取值(11.45 μm)之间的地表温度反演结果可相差0.8 ℃,因此必须引起足够的重视。
3.5 ETM+不同大气参数文件的比较
2009版的SC算法提供了5种大气参数文件,其中TIGR61、TIGR1761和TIGR2311整合了来自全球不同纬度区和季节的大气参数;STD66由MODTRAN数据中的66个不同纬度区和季节的大气轮廓参数组成;SAFREE402则包含了402个海洋区的大气轮廓参数,但Jiménez-Muñoz和Sobrino也把它应用于陆地。表 3列出了以这5种参数反演的地表温度,λ值统一采用11.45 μm。由表 3可知,没有一种大气参数文件可以稳定获得最高精度。平均来看,采用SAFREE402获得的精度最高,然后依次是TIGR2311、TIGR61、STD66、TIGR1761。
3.6 Landsat 8地表温度的反演
表 2中Landsat 8地表温度的反演精度不高,这可能与TIRS热红外传感器的定标参数不稳定有很大关系。USGS在2013年先后两次调整了其热红外波段的定标参数[10],2014年2月则用新的定标参数对全部已发布的Landsat 8数据重新处理,但TIRS 11波段仍存在不确定性。因此,USGS暂不鼓励用劈窗算法来反演地表温度。
从本次实验的结果来看,TIRS 10的误差小于TIRS 11,这可能与其波长的设置有关。由于TIRS热红外波段的波长设置在10~12 μm这一明显受大气水汽影响的范围之内,而TIRS 11所处的12 μm的波长范围比TIRS 10的10 μm所受到的影响更大,因此其误差会大于TIRS 10。总体来看,Landsat 8地表温度反演精度不高的原因可能和它过空时的大气水汽含量高达4.18 g/cm2有关。Jiménez-Muñoz和Sobrino指出,当w大于3 g/cm2时,SC算法的精度会受到影响[5]。但即便如此,TIRS 10的误差也只有-2.77 ℃。Jiménez-Muñoz和Sobrino的实验结果表明,当w下降到2 g/cm2时,误差通常会降低1.5~3 ℃。因此可以预测,如果本次实验影像的w从4.18 g/cm2下降到2 g/cm2时,其误差有可能至少下降1.5 ℃,从而使原精度误差降低一半。这使我们看到了SC算法在反演Landsat 8 地表温度上的潜力。也就是说,当大气水汽含量较低的时候,Landsat 8的地表温度可以通过SC算法单独反演TIRS 10波段来获得。本次实验还发现,如果将TIRS 10和11波段反演的地表温度取均值,则其与实测温度的误差只有0.43 ℃(表 2)。 4 结 语
Jiménez-Muñozz和Sobrino提出的SC算法对各种参数和相关算法有较严格的要求,采用正确的算法和参数,可以获得很高的精度,反之则可能造成明显的误差。
2009改进版SC算法可以明显地提高ETM+ 6波段的地表温度反演精度,因此不应继续将2003版的公式参数用于计算ETM+的地表温度。在采用2009版的算法时,要注意选用正确的大气参数文件、λ波长值,以及亮温的计算公式。对于TM 6波段,2003版和2009版的SC算法并没有实质性的差别。
在当前,Landsat 8的地表温度可以在大气水汽含量较低的情况下,通过SC算法单独反演TIRS 10波段来获得。虽然本次研究也发现,取TIRS 10和11波段反演的地表温度的均值可以获得很高的精度,但这一结果还需由更多的实验来证实。
| [1] | Georgescu M, Moustaoui M, Mahalov A, et al. Summer-time Climate Impacts of Projected Megapolitan Expansion in Arizona [J]. Nature Climate Change, 2013, 3(1):37-41 |
| [2] | Nichol J. Remote Sensing of Urban Heat Islands by Day and Night [J].Photogrammetric Engineering and Remote Sensing, 2005, 71(5):613-621 |
| [3] | Jiménez-Muñoz J C, Sobrino J A. A Generalized Single-channel Method for Retrieving Land Surface Temperature from Remote Sensing Data [J].Journal of Geophysical Research, 2003, 108(D22):4 688, doi:10.1029/2003JD003480 |
| [4] | Qin Z, Karnieli A, Berliner P. A Mono-window Algorithm for Retrieving Land Surface Temperature from Landsat TM Data and Its Application to the Israel-Egypt Border Region [J].International Journal of Remote Sensing, 2001, 22(18):3 719-3 746 |
| [5] | Jiménez-Muñoz J C, Sobrino C J, Soria J A, et al.Revision of the Single-channel Algorithm for Land Surface Temperature Retrieval from Landsat Thermal-infrared Data [J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(1):339-349 |
| [6] | Sobrino J A, Jiménez-Muñoz J C, Soria G, et al.Land Surface Emissivity Retrieval from Different VNIR and TIR Sensors [J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(2):316-327 |
| [7] | ICESS. MODIS UCSB Emissivity Library [OL].http://www.icess.ucsb.edu/modis/EMIS/html/em.html, 2013 |
| [8] | Nichol J. An Emissivity Modulation Method for Spatial Enhancement of Thermal Satellite Images in Urban Heat Island Analysis [J]. Photogrammetric Engineering and Remote Sensing, 2009, 75(5):547-556 |
| [9] | Barsi J A, Schott J R, Palluconi F D, et al.Validation of a Web-based Atmospheric Correction Tool for Single Thermal Band Instruments [C]. SPIE, San Diego, CA, 2005 |
| [10] | USGS. Landsat 8 (L8) Operational Land Imager (OLI) and Thermal Infrared Sensor (TIRS) Calibration Notices [OL]. http://landsat.usgs. gov/calibration_notices.php, 2013 |
| [11] | USGS. What are the Band Designations for the Landsat Satellites? [OL]. http://landsat.usgs.gov/band_designations_landsat_satellites.php, 2013 |
| [12] | Chander G, Markham B L, Helder D L. Summary of Current Radiometric Calibration Coefficients for Landsat MSS, TM, ETM+, and EO-1 ALI Sensors [J]. Remote Sensing of Environment, 2009, 113(5):893-903 |
| [13] | Coll C, Galve J M, Sánchez J M, et al.Validation of Landsat 7/ETM+ Thermal Band Calibration and Atmospheric Correction with Ground-Based Measurements [J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(1):547-555 |
 2015, Vol. 40
2015, Vol. 40


