文章信息
- 高广, 马洪超, 张良, 付晶
- GAO Guang, MA Hongchao, ZHANG Liang, FU Jing
- 一种顾及地形断裂线的LiDAR点云滤波方法
- A Ground Filtering Algorithm for Airborne LiDAR in Consideration of Terrain Break Lines
- 武汉大学学报·信息科学版, 2015, 40(4): 474-478
- Geomatics and Information Science of Wuhan University, 2015, 40(4): 474-478
- http://dx.doi.org/10.13203/j.whugis20130579
-
文章历史
- 收稿日期:2013-10-16
2. 宁波市测绘设计研究院, 浙江 宁波, 315042;
3. 中国电力科学研究院, 湖北 武汉, 430074
2. Ningbo Institute of Surveying and Mapping, Ningbo 315042, China;
3. China Electric Power Research Institute, Wuhan 430074, China
机载激光雷达(light detection and ranging,LiDAR)能够快速、准确地获取测区表面的三维信息,已经成为高精度数字地面模型(Digital Terrain Medel,DTM)提取的重要手段[1, 2]。LiDAR点云滤波是指从LiDAR数据中将地面点与非地面点分离开,它是提取DTM的核心技术。国内外众多学者对LiDAR点云滤波开展了大量的研究工作,并形成了基于数学形态学的滤波[3, 4, 5]、基于坡度的滤波[6, 7]、基于分割的滤波[8]等几种主流方法。但是,这些方法主要用于解决城区数据的滤波问题,专门针对山区数据的滤波算法的研究相对较少。ISPRS第三工作组对8种常用的滤波算法进行了实验比较与分析[9],特别指出现有的滤波算法在地形起伏、陡坡陡坎多,并且有植被分布的区域,存在较大的分类误差。因此,研究顾及地形断裂线的LiDAR点云滤波方法具有较强的应用价值。
Axelsson[10]于2000年提出了一种渐进加密的TIN滤波算法,但是由于商业化的原因[4],TIN滤波算法的很多细节并未公布,同时TIN滤波算法本身也还存在着一些有待改进的地方:① 在地形突变的地方,如陡坡、断裂带等,初始地面点往往难以选择到地形关键点,容易造成这些区域被平滑掉;② 当地形起伏较大时,即使已经选取了正确的初始地面点,仍有可能因为不正确的判断次序导致错分类;③ 对低矮噪声点敏感,低矮噪声点往往是某一局部区域的最低点,因此常被选取为初始地面点,进而导致低矮噪声点附近的地面点无法被正确识别。针对以上问题,本文对TIN滤波算法进行了扩展和改进,提出了一种顾及地形断裂线的LiDAR点云滤波方法。 1 理论与方法 1.1 传 统的TIN滤波算法
传统的TIN滤波算法的详细步骤如下:① 对LiDAR点云构建格网索引,所需参数一般需要人为设定;② 对于格网的每个分块,搜索其最低点作为初始地面点,并构建稀疏的地形TIN;③ 依次判断余下的脚点是否满足加入到地形TIN的条件,若满足条件,则将其加入到TIN中,并分类为地面点;④重复步骤③,直到所有点都已经被判定为地面点或非地面点。 1.2 改进的TIN加密滤波算法 1.2.1 初始地面点集的选取
初始地面点集的选取是TIN滤波算法的第一步,通常以测区内建筑物的最大边长L为单元边长划分二维格网,取每个分块内的最低点为初始地面点,该方法简单、易于实现,但是L值的合理性将直接影响初始地面点的数量和最终的滤波结果:若L值较大,初始地面点数量少,一些陡峭的区域由于缺乏地面点控制而无法保留;若L值较小,一些落在地物上的激光脚点将会被选取为初始地面点,这时算法虽然能够保留地形特征,但最终的滤波结果中将包含有大量的非地面脚点。文献[11]利用分割的方法来获取初始地面点集,在城区数据滤波中取得了不错的效果,但是这些方法需要将LiDAR点云内插成距离影像,这一过程容易引入内插误差,同时内插后的距离影像与点云也不再有一一对应的关系。本文在二维格网划分过程中引入随机参数,保证在 L值相同的情况下能够获得更多的初始地面点,具体过程如下:
1) 设置迭代次数N和最大建筑物边长L;
2) 统计点云在X、Y轴的最小值Xmin和Ymin;
3) 令二维格网的坐标原点为Porg(Xorg,Yorg),其中Porg通过式(1)计算得到:
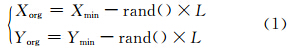
4) 以Porg和L 为参数对LiDAR点云划分二维格网,将每个分块内的最低点选取为初始地面点;
5) 重复步骤3)~4),直到迭代结束;
6) 将迭代过程中找到的地面点的并集作为TIN滤波算法的初始地面点集。 1.2.2 地面点判断准则
地面点判断准则是TIN滤波算法的核心,也是影响滤波结果的最重要因素。文献[10]中提出了两种地面点判断准则:相对地面高度和地形角。当地形平缓且连续时,利用这两种判断准则可以获得很好的滤波结果;但是对于山区数据,由于地形起伏大,且存在陡坡、陡坎等不连续地形,仅仅使用上述判断准则进行滤波容易出现地形“腐蚀”现象。针对该问题,本文提出一种地形预测角的判断准则,如图 1所示。将地形角理解为待判断的激光脚点和当前已确定地形的夹角,则地形预测角就是待判断的激光脚点与邻近地面点预测出来的地形的夹角。设待判断的激光脚点为 P0,所在三角形为△P1P2P3,则地面点判断准则分别为:
 |
| 图 1 地面点判断准则Fig. 1 Criterions of Ground Filtering |
1) 相对地面高度:P0到△P1P2P3的垂直距离d;
2) 地形角:令α、β、γ分别为P0与△P1P2P3三个顶点的夹角,则地形角θ=max(α,β,γ);
3) 地形预测角:① 查找P0到△P1P2P3的最近顶点Pi,并计算两者的距离L;② 确定Pi处的地形平面Planei,计算方法为先利用滤波过程中已经建立好的地面点TIN结构来获取Pi在半径R内的K近邻地面点N(Pi)={(x1,y1,z1),…,(xk,yk,zk)},令平面方程为Z=aX+bY+c,构造超定线性方程组如式(2)所示,采用最小二乘法求解得到平面方程,Planei的法向量为 V =(-a,-b,1)T;③计算P0Pi与地形平面Planei的夹角δ,即P0Pi与法向量 V 的夹角的余角,本文将δ称为P0相对于△P1P2P3的地形预测角。
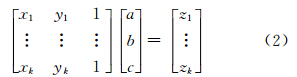
如果待判断的激光脚点满足以下条件中的任意一个,则判定其为地面点:①d<Td且θ<Tθ;②L<TL且δ<Tδ;其中Td为相对地面高度阈值,Tθ为地形角阈值,TL为与最近地面点的距离阈值,一般取2~3倍的点间距为宜,Tδ为地形预测角阈值。 1.2.3 使用优先队列进行加密滤波
加密顺序是TIN滤波算法中常被忽略的一个环节。文献[12]指出,如果不对数据进行排序而直接滤波,会导致滤波结果中存在较多噪声。如图 2所示,P0、P1分别是区域A、B的局部低点,算法开始时,将其选择为初始地面点,而P2是 落在低矮植被上的待判断点,由于P2 满足相对地面高度和地形角阈值条件,因而被错误地分类为地面点。特别是在算法的开始阶段,地形还很粗糙,这种由于地形起伏而造成低矮植被被错分的情况更容易发生。为此,本文使用优先队列[13]来优化TIN加密顺序,在优先队列中,每个激光脚点都被赋予一个与距离相关的加密优先级,具有最高优先级的元素最 先访问。算法的详细步骤如下:
 |
| 图 2 地形起伏对滤波结果的影响Fig. 2 The Effects of Terrain Variation on Filtering Result |
1) 假设已找到的地面点集 为A,待判断点集为B,搜索半径为kR,增长比率为k,优先队列为PQ;
2) 将点集B中候选点的优先级设置为0;
3) 如果点集B为空,则算法结束,A为得到的最终地面点集;否则,构造优先队列PQ。对于B中的每个候选激光脚点bi,查找A中与bi最接近的脚点aj,计算两者间的距离d,如果d小于R,则bi的优先级priority(bi)=e-d,将bi加入到优先队列PQ中,并从B中删除;
4) 从优先队列PQ中取出优先级最高的候选激光脚点Pi,根据上一节介绍的地面点判断准则,判断Pi是否满足地面点条件,如果满足条件,则将Pi加入到A中,转步骤5),否则转步骤6);
5) 重新计算Pi为半径R内的候选点的优先级,如果计算出来的新优先级大于原优先级,则更新候选点在优先队列中的位置。这里有两种情况:① 待更新优先级的脚点还未加入到优先队列中,将其加入到优先队列中,并从B中删除;② 待更新优先级的脚点已经在优先队列中,则只更新其在优先队列中的位置;
6) 重复步骤4)~5),直到优先队列为空;
7) 扩大搜索半径为kR,转步骤2),重新构造优先队列。
该算法优先考虑地面点附近的候选激光脚点,实际上算法是以地面点为中心、逐步向外扩散的方式进行滤波的。 1.3 低矮点剔除
基于局部最低点的TIN加密滤波算法对低矮噪声点敏感,传统的滤波流程试图在算法开始前先剔除噪声点,但由于缺乏足够的信息,效果并不理想。本文认为,随着算法的进行,地形的细节信息越来越丰富,使得低矮噪声点的剔除更容易,也更可靠。在此提出一种高差分析的低矮点剔除方法,该方法的优点是不仅可以剔除单个低矮点,而且可以剔除多个低矮点形成的点集。算法的具体步骤如下:
1) 对于某个待判别点P0,计算其K邻域地面点{P1,…,Pk},将其按Z值从小到大排序,得到有序数组V={Pi0,Pi1,…,Pik};
2) 计算有序数组V中相邻点间的高差D={di0,di1,…,dik-1},其中dij=Pij+1-Pij;
3) 从j=0开始,计算判别式(3)是否为真,如果为真,则将点P0分类成低矮点。

式中,Zthreshold为允许的最大高差;nmax为噪声点集的最大点数。
需要指出的是,在完成低矮噪声点剔除后,还应该对低矮点附近的脚点重新进行滤波处理,找回被误判的地面点。 2 实验结果与分析
2 .1 实验数据与定性分析
为了检验算法的有效性,在LiDAR数据处理平台ALDPro中实现了本文算法,选取两块典型的分布有大量地形断裂线的LiDAR点云作为实验数据,数据已事先手工分类,后续将手工分类的结果作为真值来检查算法的滤波效果。
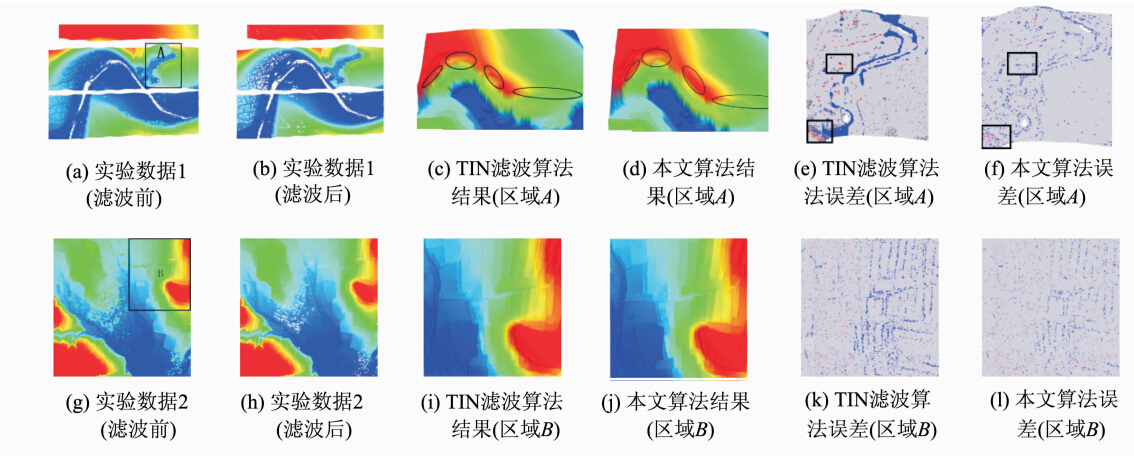
实验数据1为ISPRS提供的滤波测试数据Site 5,实验区内包含有稀疏的人工建筑物,地形变化大,多陡坡、陡坎,还有少量植被,针对该类型复杂地表数据的判别需要进一步的研究。图 3(a)是滤波前的LiDAR数据,图 3(b)是利用本文算法得到的滤波结果,图 3(c)是采用TIN滤波算法得到的区域A的滤波结果。可以看出,TIN滤波算法在陡坡、陡坎处(椭圆圈出的地方)有严重的“腐蚀”现象。图 3(d)是采用本文算法得到的区域A的滤波结果,与图 3(c)相比,图 3(d)中陡坡、陡坎等地形信息保留相对完整。图 3(e)是TIN滤波算法的误差分布图,其中蓝色像素表示该处的地面点没有被识别出来,红色像素表示该 处的地物点被错误地分类成地面点,灰色像素表示该处分类正确。图 3(e)说明TIN滤波算法在地形不连续区域具有较多错分类的情况,同时,在分布有植被的地形起伏区域(矩形框出的地方)出现较多地物点被分类成地面点的现象。图 3(f)是图 3(d)的误差分布图,可以看出在陡坡、陡坎区域的蓝色像素明显减少,同时低矮植被密集的区域(矩形框出的地方)的滤波效果 也得到了改善。
 |
| 图 3 实验数据及滤波结果比较Fig. 3 Experiment Data and Comparison of Filtering Results |
实验数据2采自河南某山区,实验区内包含村庄、梯田和低矮植被。图 3(g)是滤波前的LiDAR数据,图 3(h)是利用本文算法得到的滤波结果,图 3(i)是区域B经TIN滤波算法处理后的滤波结果,图 3(j)是区域B采用本文算法处理后的滤波结果。可以看出,经本文算法处理后,绝大部分的低矮植被点均被正确剔除,地形断裂处也保留得较完整。对比图 3(i)和图 3(j)可以看出,TIN滤波算法提取的地形边缘比较模糊,而本文算法提取的地形边缘较清晰;对比图 3(k)和图 3(l)可以看出,对TIN滤波算法进行改进后,代表错误滤波的红色像素和蓝色像素都明显减少,特别是在梯田的边缘处。 2.2 定量分析
本文采用文献[9]提出的滤波算法评价体系:滤波算法的效果可以用Ⅰ类误差、Ⅱ类误差和总误差来描述,其中Ⅰ类误差表示地面点被错分类成非地面点的百分比,Ⅱ类误差表示非地面点被错分类成地面点的百分比,总误差表示所有被错分类的激光脚点所占的百分比。表 1给出了改进前的TIN滤波算法与改进后的TIN滤波算法的统计结果。从表 1可以看出:① 利用随机化的格网搜索算法获取的初始地面点的数量是改进前的10倍以上,大量的初始地面点为算法提供了更加精确的初始地形信息,是算法成功的重要基础;② 改进后的TIN滤波算法的各类误差均小于改进前TIN滤波算法,其中Ⅰ类误差的降低幅度最为明显,这是因为所选取的实验区的主要地形特征是陡坡、陡坎,这也表明本文提出的改进对于保留山区地形断裂线是非常有效的。
| TIN滤波算法 | 改进后的TIN滤波算法 | |||||||
| 初始地面点数/个 | Ⅰ类误差/% | Ⅱ类误差/% | 总误差/% | 初始地面点数/个 | Ⅰ类误差/% | Ⅱ类误差/% | 总误差/% | |
| 区域A | 686 | 8.58 | 16.76 | 8.91 | 8 152 | 5.90 | 15.60 | 6.30 |
| 区域B | 1 281 | 9.48 | 8.91 | 9.07 | 12 740 | 4.54 | 7.61 | 5.87 |
本文针对山区LiDAR点云的特点,提出了一种顾及地形断裂线的TIN滤波算法。针对两组分布有大量地形断裂线的山区数据进行滤波实验,并与改进前的TIN滤波算法进行了定性和定量分析。结果表明,改进后的TIN滤波算法可以明显地提高山区LiDAR点云的滤波精度。需要指出的是,本文算法虽然是针对山区LiDAR点云滤波问题提出的,但它同样适用于城区场景的LiDAR点云滤波问题;主要存在的问题是算法的时间复杂度较高,以牺牲效率来达到提高滤波精度的目的。
| [1] | Baltsavias E P. A Comparison Between Photogrammetry and Laser Scanning[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 1999, 54(2/3):83-94 |
| [2] | Razak K A, Santangelo M, Van Westen C J, et al. Generating an Optimal DTM from Airborne Laser Scanning Data for Landslide Mapping in a Tropical Forest Environment[J]. Geomorphology, 2013, 190:112-125 |
| [3] | Zhang K, Chen S C, Whitman D, et al. A Progressive Morphological Filter for Removing Nonground Measurements from Airborne LiDAR Data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(4):872-882 |
| [4] | Chen Q, Gong P, Baldocchi D, et al. Filtering Airborne Laser Scanning Data with Morphological Methods[J]. Photogrammetric Engineering and Remote Sensing, 2007, 73(2):175-185 |
| [5] | Pingel T J, Clarke K C, McBride W A. An Improved Simple Morphological Filter for the Terrain Classification of Airborne LiDAR Data[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2013, 77:21-30 |
| [6] | Sithole G. Filtering of Laser Altimetry Data Using a Slope Adaptive Filter[J]. International Archives of Photogrammetry Remote Sensing and Spatial Information Sciences, 2001, 34(3/W4):203-210 |
| [7] | Susaki J. Adaptive Slope Filtering of Airborne LiDAR Data in Urban Areas for Digital Terrain Model (DTM) Generation[J]. Remote Sensing, 2012, 4(6):1 804-1 819 |
| [8] | Sithole G. Segmentation and Classification of Airborne Laser Scanner Data[D]. The Netherland:Delft University of Technology, 2005 |
| [9] | Sithole G, Vosselman G. Experimental Comparison of Filter Algorithms for Bare-Earth Extraction from Airborne Laser Scanning Point Clouds[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2004, 59(1):85-101 |
| [10] | Axelsson P. DEM Generation from Laser Scanner Data Using Adaptive TIN Models[J]. International Archives of Photogrammetry and Remote Sensing, 2000, 33(B4/1, PART 4):111-118 |
| [11] | Zhang J, Lin X. Filtering Airborne LiDAR Data by Embedding Smoothness-constrained Segmentation in Progressive TIN Densification[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2013, 81:44-59 |
| [12] | Sui Lichun, Zhang Yibin, Zhang Shuo, et al. Filtering of Airborne LiDAR Point Cloud Data Based on Progressive TIN[J]. Geomatics and Information Science of Wuhan University, 2011, 36(10):1 159-1 163(隋立春, 张熠斌, 张硕, 等. 基于渐进三角网的机载LiDAR点云数据滤波[J]. 武汉大学学报·信息科学版, 2011, 36(10):1 159-1 163) |
| [13] | Emde Boas P, Kaas R, Zijlstra E. Design and Implementation of an Efficient Priority Queue[J]. Mathematical Systems Theory, 1976, 10(1):99-127 |
 2015, Vol. 40
2015, Vol. 40


