文章信息
- 张卡, 盛业华, 管忠诚, 李佳
- ZHANG Ka, SHENG Yehua, GUAN Zhongcheng, LI Jia
- 基于NSCT的立体影像匹配相似性测度计算
- NSCT Based Computation of Similarity Measure for Stereo Image Matching
- 武汉大学学报·信息科学版, 2015, 40(4): 457-461
- Geomatics and Information Science of Wuhan University, 2015, 40(4): 457-461
- http://dx.doi.org/10.13203/j.whugis20130346
-
文章历史
- 收稿日期:2013-07-23
2. 南京师范大学江苏省地理信息资源开发与利用协同创新中心, 江苏 南京, 21002;
3. 南京师范大学警用地理信息技术公安部重点实验室, 江苏 南京, 210023;
4. 青岛市市政工程设计研究院有限责任公司, 山东 青岛, 266101
2. Jiangsu Center for Collaborative Innovation in Geographical Information Resource Development and Application, Nanjing Normal University, Nanjing 210023, China;
3. Key Laboratory of Police Geographic Information Technology Ministry of Public Security, Nanjing Normal University, Nanjing 210023, China;
4. Qingdao Municipal Engineering Design & Research Institute Co. Ltd., Qingdao 266101, China
立体影像匹配的目的是根据一幅影像上的已知模式(点、线、面),从同一场景下拍摄的另一幅影像上寻找相对应的同名模式,是遥感影像配准、数字摄影测量、虚拟地理场景重建等领域的核心技术[1, 2, 3]。相似性测度模型的设计与计算是立体影像匹配的首要任务,对匹配结果的可靠性具有重要的影响,即数字立体摄影测量中的同名点相似性测度计算问题。这也是本文的研究重点。
立体影像中的同名点相似性测度是指左影像上待匹配点的目标窗口和右影像上候选点的搜索窗口之间的相似程度,这是判断两个像点是否为同名像点的依据,可基于影像的灰度分布计算,也可基于影像的后处理特征计算。常用的灰度相似性测度有归一化互相关系数(normalized cross correlation,NCC)[1]、截断绝对差(truncated absolute difference,TAD)[4]、差平方和(sum of squared difference,SSD)[5]、差绝对值和(sum of absolute difference,SAD)[6]等。基于灰度的相似性测度在影像的信息贫乏区域的匹配成功率不高,因此,基于特征的相似性测度方法得到了重视,先对影像进行某种特征变换,如(scale invariant feature transform,SIFT)[7]、小波变换[8]、Contourlet变换[9]等,以构建匹配窗口的特征向量,然后再计算特征向量间的NCC、欧氏距离等度量值作为匹配测度。但是,以上这些相似性测度计算方法大都没有考虑匹配窗口内待匹配点(中心像素)与其邻域像素之间的异质性特征,窗口内各个像素在参与测度计算时被同等对待,这导致匹配测度在适应性和抗干扰性方面存在一定的问题。基于此,Yoon等[10, 11, 12, 13]考虑到匹配窗口内的像素与中心像素之间的颜色和空间距离相似性,提出了多种加权匹配测度计算方法。然而,这几种加权测度的计算模型仅使用了像素间的颜色相似性和空间距离进行加权,并未考虑到权值计算中影像本身的结构特征;而且,在影像中的视差不连续处,像素间的空间距离远近不能有效地度量像素之间的异质性特征。 因此,本文提出了一种基于非下采样Contourlet变换(Nonsubsampled Contourlet Transform,NSCT)的相似性测度计算方法。
1 基于NSCT的相似性测度计算原理 1.1 NSCT基本原理
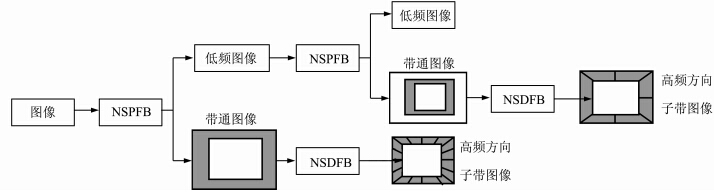
NSCT是在Contourlet变换的基础上发展而成的新型图像多尺度几何分析工具[9],其结构与Contourlet变换很相似,但NSCT在图像的分解和重构过程中取消了下采样环节,从而使得NSCT不仅具有多尺度性、良好的空域和频域局部特性和方向特性,还具有平移不变特性。NSCT最突出的特点是具有强大的各向异性,相比于小波变换的高频信息只有水平、垂直、对角线三个方向分量的信息,NSCT能够将高频信息分解为多个方向性分量的组合,此种结构使得NSCT具有良好的非线性逼近能力,它可以对任意含线性奇异的二维分段光滑函数进行近似地逼近。NSCT的基本过程为:先采用非采样塔式滤波器组(nonsubsampled pyramid filter bank,NSPFB)获得图像的多尺度分解,然后再采用非采样方向滤波器组(nonsubsampled directional filter bank,NSDFB)对得到的各尺度带通子带图 像进行方向分解,从而得到不同尺度、不同方向的高频子带图像。图像经过J级(J≥1,为变换级数参数) NSCT 分解变换后,可以得到一个低频近似图像和 个方向高频子带图像(di为各级变换中的高频分解的方向参数,2di为各级变换中的高频方向子带图像的个数),而且它们的分辨率都和原图像相同。NSCT的分解示意图如图 1所示。
个方向高频子带图像(di为各级变换中的高频分解的方向参数,2di为各级变换中的高频方向子带图像的个数),而且它们的分辨率都和原图像相同。NSCT的分解示意图如图 1所示。
|
| 图 1 NSCT的分解示意图 Fig. 1 Decomposition Sketch of NSCT |
对立体影像中的左影像f(x,y)、右影像f′(x,y),分别进行n级多方向NSCT变换(每级的方向数为di,i=1,2,…,n),以得到左、右影像的m= 个高频方向子带系数影像Gj(x,y)、G′ j(x,y)(j=1,2,…,m)。此时,左影像或右影像中的任意一个像素p(x,y)不仅可用R、G、B三个通道的灰度值组成颜色特征向量 c(p)=(fR(x,y),fG(x,y),fB(x,y)),还可用m个高频方向的子带系数组成结构特征向量V G(p)=(G1(x,y),G2(x,y),…,Gm(x,y))。因此,在计算匹配测度的过程中,先根据格式塔理论的相似性和接近性原则[13],用特征向量间的欧几里德距离和高斯函数来度量窗口中心像素pc(xc,yc)与其邻域像素pk(xk,yk)之间的颜色相似性Sc和结构接近性PG
个高频方向子带系数影像Gj(x,y)、G′ j(x,y)(j=1,2,…,m)。此时,左影像或右影像中的任意一个像素p(x,y)不仅可用R、G、B三个通道的灰度值组成颜色特征向量 c(p)=(fR(x,y),fG(x,y),fB(x,y)),还可用m个高频方向的子带系数组成结构特征向量V G(p)=(G1(x,y),G2(x,y),…,Gm(x,y))。因此,在计算匹配测度的过程中,先根据格式塔理论的相似性和接近性原则[13],用特征向量间的欧几里德距离和高斯函数来度量窗口中心像素pc(xc,yc)与其邻域像素pk(xk,yk)之间的颜色相似性Sc和结构接近性PG
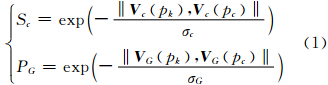
式中,V c(pk)、 V c(pc)分别是局部窗口影像中第k个像素和中心像素的颜色特征向量;V G(pk)、 V G(pc)分别是第k个像素和中心像素的结构特征向量;‖,‖表示两个向量之间的欧几里德距离;σc、σG为高斯函数的参数(可根据需要赋值)。
基于式(1),窗口影像中的每个像素与中心像素之间的权值为w(pk,pc)= Sc×PG。至此,对于左影像中以待匹配点pc为中心的大小为N×N的目标窗口影像Wt,右影像中以搜索点qc为中心的大小为N×N的搜索窗口影像Ws,利用目标窗口、搜索窗口中第k个像素的颜色特征向量 V c(pk)、 V c(qk)和高频结构向量 V G(pk)、 V ′ G(qk),先计算像素k和中心像素之间的权值wt(pk,pc)、ws(qk,qc);然后在SAD相似度的基础上,按式(2)计算两个窗口中对应像素之间的差绝对值相似度ρ(pk,qk);最后,设计出如式(3)所示的基于 NSCT结构特征和RGB颜色特征的加权匹配测度。
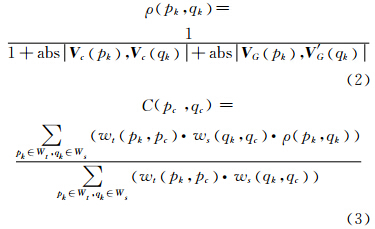
为了验证本文匹配方法的实际效果,在Windows XP环境下,采用MATLAB 2007a科学计算语言对本文算法进行了编程实现,并使用美国Middlebury大学开发的影像匹配方法在线测试评估平台[5](http://vision.middlebury.edu/stereo/)提供的4对标准立体影像(如图 2所示,其中,上面一行为立体像对的左影像,下面一行为该像对的真实视差图;像对的名称从左往右依次为Tsukuba、Venus、Teddy、Cones),进行如下两个实验:① NSCT变换参数的尺度效应分析实验,以确定具有最优匹配准确度的NSCT最佳变换级数和方向数;② 不同相似性测度的匹配可靠性对比实验,以比较本文加权相似性测度与现有几个相似性测度的匹配结果的优劣。实验中,匹配窗口的尺寸均为35 像素×35 像素,σc、σG也都取匹配窗口的尺寸值,匹配准确度的定量衡量指标为测试平台给出的Nonocc、All、Disc、Avg,Nonocc、All、Disc分别表示匹配视差图结果中的非遮挡区域、像对重叠区域、视差不连续区域的错误匹配率,Avg表示4对立体像对的总体平均错误匹配率(错误匹配率是指匹配视差图中的匹配视差与真实视差间较差大于1个像素的像素个数占图像总像素数的比率)。以上4个指标值越小,则说明匹配方法的匹配可靠性越高。

|
| 图 2 标准立体影像及其真实视差图 Fig. 2 Standard Stereo Images and True Disparity Maps |
1) NSCT变换参数的尺度效应分析实验
此实验的目的是确定NSCT的最佳变换级数和方向参数,以使本文中基于NSCT的加权相似性测度能取得最优的匹配可靠性。首先,进行NSCT的最佳方向参数实验:在保持变换级数固定的情况下(1级变换),方向数参数分别取1、2、3、4,将各个方向参数下的匹配视差图像提交到在线测试平台,根据不同方向参数下的匹配错误率指标,确定具有最低匹配错误率的方向参数。然后,进行NSCT的最佳变换级数实验:在保持每级的方向参数都是所确定的最佳方向参数的情况下,变换级数分别取1、2、3、4,将各个变换级数下的匹配视差图像提交到在线测试平台,根据不同变换级数下的匹配错误率指标,确定具有最低匹配错误率的变换级数。在此实验中,NSCT的变换级数和方向参数都只取了有限的几个值,这主要是因为太大的变换参数会使得NSCT分解的高频系数图像的个数呈指数级增加,反而会降低立体影像匹配的运行效率。NSCT尺度效应实验所得到的错误匹配率与尺度参数之间的统计数据见表 1,将最低平均错误匹配率的所在行加粗显示。从表 1的实验结果可以看出,当NSCT的方向参数取3,即高频系数图像个数为8个时,4个立体像对的平均错误匹配率在此取值情况下最小;在每级的方向参数都取3的情况下,当变换级数为2,即进行二级NSCT分解时,4个立体像对的平均错误匹配率指标最小。因此,NSCT的最佳变换参数为:变换级数取2,方向参数取3。
| NSCT 参数 | Tsukuba | Venus | Teddy | Cones | Avg | |||||||||
| Nonocc | All | Disc | Nonocc | All | Disc | Nonocc | All | Disc | Nonocc | All | Disc | |||
| 方向 | 1 | 4.28 | 5.82 | 11.0 | 2.06 | 3.56 | 8.16 | 13.3 | 22.0 | 23.8 | 10.1 | 19.8 | 17.8 | 11.8 |
| 2 | 4.25 | 5.76 | 11.6 | 1.72 | 3.23 | 8.07 | 12.3 | 21.1 | 22.9 | 7.36 | 17.3 | 14.9 | 10.9 | |
| 3 | 3.83 | 5.32 | 11.9 | 1.36 | 2.89 | 8.37 | 11.5 | 20.5 | 22.6 | 5.68 | 15.8 | 12.8 | 10.2 | |
| 4 | 4.28 | 5.76 | 12.9 | 2.3 | 3.84 | 14.1 | 11.6 | 20.5 | 24.5 | 5.29 | 15.4 | 12.5 | 11.1 | |
| 比例 | 1 | 3.83 | 5.32 | 11.9 | 1.36 | 2.89 | 8.37 | 11.5 | 20.5 | 22.6 | 5.68 | 15.8 | 12.8 | 10.2 |
| 2 | 3.19 | 4.68 | 12 | 1.31 | 2.85 | 10.7 | 10.9 | 19.9 | 22.9 | 4.99 | 15.1 | 12.3 | 10.1 | |
| 3 | 3.57 | 5.18 | 15.1 | 2.39 | 3.94 | 22.6 | 11.5 | 20.5 | 22.6 | 5.61 | 15.8 | 14.6 | 11.9 | |
| 4 | 4.92 | 6.77 | 20 | 4.99 | 6.51 | 34.9 | 12.1 | 21.0 | 27.1 | 7.39 | 17.5 | 18.3 | 15.1 | |
2) 不同相似性测度的对比实验
此实验的目的是将本文NSCT加权相似性测度(变换级数和方向参数分别为2和3)和现有的8个相似性测度进行比较,以验证本文相似性测度的匹配可靠性。参与比较的其他8个相似性测度分别为NCC测度[1](采用R、G、B三个通道的NCC平均值作为最终的NCC测度)、SAD测度[6]、SIFT测度[7]、SIFT-Color综合测度、基于相位的PhaseDiff测度[8]、DGBGrid加权测度[11]、BioPsyASW加权测度[12]和LCDM+Adapt加权测度[13]。将不同相似性测度对4对标准立体像对生成的匹配视差图提交给在线测试平台,得到不同相似性测度的错误匹配率统计结果,见表 2,将各个指标中的最小值加粗显示。从实验结果可以看出,对于4对标准立体影像,本文加权测度所生成的视差图(图 3)在定量评价指标上具有最小的总体平均错误匹配率。另外,从每一对立体影像的匹配结果来看,本文方法的错误匹配率指标基本上都较小。相比于传统的基于灰 度的NCC测度和基于SIFT特征的测度,本文方法的错误匹配率要降低2倍以上。由此可见,本文的加权测度能很好地顾及匹配窗口内邻域像素之间的异质性特征,并通过赋予每个像素不同的权值来决定它们对最终相似性测度计算的贡献,从而提高了匹配结果的可靠性。
| NSCT 参数 | Tsukuba | Venus | Teddy | Cones | Avg | ||||||||
| Nonocc | All | Disc | Nonocc | All | Disc | Nonocc | All | Disc | Nonocc | All | Disc | ||
| NSCT | 3.19 | 4.68 | 12 | 1.31 | 2.85 | 10.7 | 10.9 | 19.9 | 22.9 | 4.99 | 15.1 | 12.3 | 10.1 |
| NCC | 15.1 | 16.6 | 46.9 | 8.95 | 10.4 | 42 | 28.6 | 35.9 | 52.3 | 23.4 | 31.6 | 43.5 | 29.6 |
| SIFT | 12.7 | 14.6 | 44.6 | 17.9 | 19.2 | 44.6 | 25.9 | 33.5 | 49.6 | 16.8 | 25.9 | 40 | 28.8 |
| SIFT-Color | 11.3 | 13.2 | 44.2 | 10.5 | 12 | 41.9 | 23.4 | 31.2 | 49.2 | 16.1 | 25.2 | 37.8 | 26.3 |
| SAD | 4.87 | 5.89 | 22.9 | 2.50 | 3.22 | 18.3 | 18.2 | 18.7 | 37.2 | 24.2 | 27.9 | 42.1 | 18.8 |
| PhaseDiff | 4.89 | 7.11 | 16.3 | 8.34 | 9.76 | 26.0 | 20.0 | 28.0 | 29.0 | 19.8 | 28.5 | 27.5 | 18.8 |
| DGBGrid | 5.90 | 7.26 | 21.0 | 1.35 | 1.91 | 11.2 | 10.5 | 17.2 | 22.2 | 5.34 | 11.9 | 14.9 | 10.9 |
| BioPsyASW | 3.62 | 5.52 | 14.6 | 3.15 | 4.20 | 20.4 | 11.5 | 18.2 | 23.2 | 4.93 | 13.0 | 11.7 | 11.2 |
| LCDM+Adapt | 5.98 | 7.84 | 22.2 | 14.5 | 15.4 | 35.9 | 20.8 | 27.3 | 38.3 | 8.90 | 17.2 | 20.0 | 19.5 |

|
| 图 3 本文NSCT匹配测度所生成的标准立体像对的视差图 Fig. 3 Disparity Maps Generated by Proposed NSCT Similarity Measure for Standard Stereo Images |
本文针对立体影像匹配中相似性测度的稳健计算需求,采用NSCT这一新型的图像多尺度几何分析工具,提出了一种基于NSCT的加权相似性测度计算方法。使用国际上公认的影像匹配在线测试评估平台提供的标准立体影像,对本文算法进行了实验检验和在线测试,并将本文方法和现有一些方法进行了对比实验,实验结果验证了本文方法的有效性,错误匹配率明显降低。另外,本文还对NSCT尺度参数在立体影像匹配中的尺度效应问题进行了实验分析,得到了具有最优匹配结果的NSCT最佳变换参数。但是,由于本文算法是在MATLAB平台上编程实现的,受限于MATLAB编译效率,运行效率并不高。不过,由于本文主要目的是定量比较不同匹配测度的匹配结果的可靠性,因此并未对各种匹配测度的计算效率进行定量对比。
| [1] | Yang H C, Zhang S B, Wang Y B. Robust and Precise Registration of Oblique Images Based on Scale-invariant Feature Transformation Algorithm[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(4):783-787 |
| [2] | Ji Song, Fan Dazhao, Zhang Yongsheng, et al. MVLL Multi-image Matching Model and Its Application in ADS40 Linear Array Images[J]. Geomatics and Information Science of Wuhan University, 2009, 34(1):28-31 (纪松, 范大昭, 张永生, 等.多视匹配MVLL算法及其在ADS40线阵影像中的运用[J].武汉大学学报5信息科学版, 2009, 34(1):28-31) |
| [3] | Snavely N, Seitz S M, Szeliski R. Modeling the World from Internet Photo Collections[J]. International Journal of Computer Vision, 2008, 80(2):189-210 |
| [4] | Yang Q, Wang L, Ahuja N. A Constant-space Belief Propagation Algorithm for Stereo Matching[C]. IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, America, 2010 |
| [5] | Scharstein D, Szeliski R. A Taxonomy and Evaluation of Dense Two-frame Stereo Correspondence Algorithms[J]. International Journal of Computer Vision, 2002, 47(1/2/3):7-42 |
| [6] | Manap N A, Soraghan J J. Disparity Refinement Based on Depth Image Layers Separation for Stereo Matching Algorithms[J]. Journal of Telecommunication, Electronic and Computer Engineering, 2012, 4(1):51-64 |
| [7] | Lowe D G. Distinctive Image Features from Scale-invariant Feature Transform[J]. International Journal of Computer Vision, 2004, 60(2):91-110 |
| [8] | El-Etriby S, Al-Hamadi A, Michaelis B. Dense Depth Map Reconstruction by Phase Difference -based Algorithm Under Influence of Perspective Distortion[J]. International Journal Machine Graphics and Vision, 2006, 15 (3):349- 361 |
| [9] | Cunha A L, Zhou J P, Do M N. The Nonsubsampled Contourlet Transform:Theory, Design, and Applications[J]. IEEE Transactions on Image Processing, 2006, 15(10):3 089-3 101 |
| [10] | Yoon K J, Kweon I S. Adaptive Support-weight Approach for Correspondence Search[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2006, 28(4):650-656 |
| [11] | Richardt C, Orr D, Davies I, et al. Real-time Spatiotemporal Stereo Matching Using the Dual-cross-bilateral Grid[J]. Lecture Notes in Computer Science, 2010, 6 313:510-523 |
| [12] | Nalpantidis L, Gasteratos A. Biologically and Psychophysically Inspired Adaptive Support Weights Algorithm for Stereo Correspondence[J]. Robotics and Autonomous Systems, 2010, 58(5):457-464 |
| [13] | Nalpantidis L, Gasteratos A. Stereo Vision for Robotic Applications in the Presence of Non-ideal Lighting Conditions[J]. Image and Vision Computing, 2010, 28(6):940-951 |
 2015, Vol. 40
2015, Vol. 40


