文章信息
- 韦春桃, 张祖勋, 张剑清, 吴平
- WEI Chuntao, ZHANG Zuxun, ZHANG Jianqing, WU Ping
- 分层Fourier-Melin变换相位相关的影像匹配初始视差的自动获取方法
- A Method for Automatically Determining Parallax of Image Matching Based on Layered Fourier-Melin Phase Correlation
- 武汉大学学报·信息科学版, 2015, 40(4): 452-456
- Geomatics and Information Science of Wuhan University, 2015, 40(4): 452-456
- http://dx.doi.org/10.13203/j.whugis20130354
-
文章历史
- 收稿日期:2013-07-24
2. 桂林理工大学测绘地理信息学院, 广西 桂林, 541004;
3. 武汉大学遥感信息工程学院, 湖北 武汉, 430079;
4. 福建省基础地理信息中心, 福建 福州, 350001
2. College of Geomatics and Geoinformation, Guilin University of Technology, Guilin 541004, China;
3. School of Remote Sensing and Information Engineering, Wuhan University, Wuhan 430079, China;
4. Fujian Provincial Geomatics Center, Fuzhou 350001, China
影像匹配是数字摄影测量的核心问题,快速准确地确定立体影像对的初始视差,亦即匹配初值,是影像匹配自动化的难题。准确的初始视差可以缩小匹配搜索范围,减少在纹理重复和纹理贫乏等区域的匹配混淆,提高匹配效率、精度和可靠性,同时为最小二乘等高精度匹配方法提供精确的初始值。
目前在实际工作中常用的确定初始视差方法有: (1) 人工选取对应匹配点对方法。该方法易受人为主观操作因素和影像分辨率的影响而产生选取误差,且需人工干预,不能实现完全的自动化。(2) 影像灰度相关法。该方法通过对立体影像计算在水平方向和垂直方向具有不同偏移量时两张影像的灰度相关系数,将具有最大相关系数时的偏移量作为初始视差[1, 2, 3],存在计算量大,效率低下,在影像信息贫乏、纹理重复区域很难正确确定影像的初始视差,可靠性不高,且不具有旋转不变性等缺点。(3) 利用立体影像水平与垂直两方向的重叠度来估计初始视差。由于航空摄影时飞行不平稳,航向和旁向会出现各种偏差和抖动,从而影响初始视差的估计,准确度较低[3]。(4) 利用POS系统提供的像片近似外方位元素来确定初始视差。该方法可靠性较高,但精度受POS观测值精度的影响,直接利用POS 提供的定向参数进行初始视差估计精度较低[2]。(5) 影像特征匹配法,对两张立体影像分别提取特征,然后进行特征匹配和其他信息确定初始视差[1, 2, 3]。特征匹配法确定初始视差依赖于特征提取的准确性,使用范围也有一定的局限。
频率域相位相关和Fourier-Melin(FM)变换常被用于影像配准[4, 5, 6, 7]中,主要用于解算两幅待配准影像之间的整体平移、缩放和旋转参数。本文将Fourier-Melin变换和相位相关方法用于金字塔影像中,获取两幅待匹配影像的初始视差,提出了一种分层Fourier-Mellin相位相关的影像匹配初始视差的自动获取方法。该方法的特点是不需要任何先验阈值和辅助信息(如相机参数、POS数据、影像重叠度等),能够自动获取影像匹配较精确的初始视差。实验证明了该方法的有效性。
1 基于Fourier-Mellin变换的相位相关方法 1.1 相位相关法
相位相关[8, 9]是一种非线性的、基于傅里叶功率谱的频域相关技术,其理论依据是傅里叶平移定理,信号在空间域上的平移产生频率域上成比例的相位平移,常用于检测两幅影像之间的平移量。假设两幅影像 f1(x,y)和f2(x,y)之间有如下平移关系:

若F1(u,v)和F2(u,v)分别为f1(x,y)和f2(x,y)的傅里叶变换,根据傅里叶平移定理有:

两影像f1(x,y)和f2(x,y)的互功率谱为:
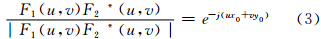
式中,F2*(u,v)为F2(u,v)的复共轭;e-j(ux0+vy0)的傅里叶逆变换为一个二维脉冲函数δ(x-x0,y-y0)。相位相关法就是求取式(3)的傅里叶逆变换,通过搜索峰值位置来确定平移参数x0和y0。在频率域利用相关技术能够快速地找到最佳匹配位置。
1.2 基于Fourier-Mellin变换的相位相关法
相位相关对影像间的旋转非常敏感,实验数据表明,当旋转角度达到±3°时,脉冲幅度被完全淹没在噪声中,相位相关失效。基于 Fourier-Mellin变换的相位相关法[10]是一种基于Fourier-Mellin变换旋转-缩放不变性和Fourier变换平移定理的变换参数估计算法,可以较好地解决影像间的旋转、缩放和平移问题。假设影像 f1(x,y)与f2(x,y)之间存在旋转、缩放和平移变换,即:
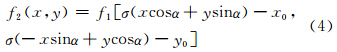
式中,σ、α、(x0,y0)分别是缩放、旋转、平移参数。则f1(x,y)和f2(x,y)对应的傅里叶变换F1(u,v)和F2(u,v)之间满足:
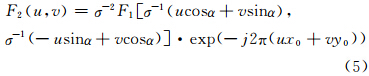
分别提取F1 和F2 的幅度,有

从式(6) 可以看出,两影像频谱的幅度只与缩放因子σ和旋转角度α有关,与平移量(x0,y0)无关,因此,可以将缩放因子、旋转角度与平移量进行分离计算。将两幅影像的幅度谱分别变换至极坐标系ρ-θ下,令u=ρcosθ,v=ρsinθ,得:
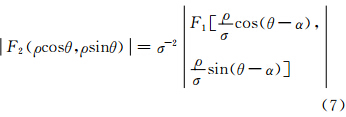
令f2p(ρ,θ)= F2(ρcosθ,ρsinθ) ,f1p(ρ,θ)= F1(ρcosθ,ρsinθ) ,则式(7)可表示为:
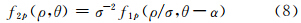
对式(8)的极径轴ρ进行对数变换,得:
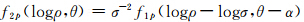
设λ=logρ,k=logσ,变量代换后为:
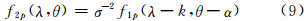
式(9)说明,在转换至对数极坐标后,缩放与旋转变换己被转换为平移变换。式(9)与式(1)具有相同的形式,因此可以应用相位相关法求解。在对数-极坐标空间应用相位相关法求出k和α,若对数的底取为e,则σ=ek,这样得到影像之间的缩放因子σ和旋转角度α,之后利用计算出的σ和α对原影像进行缩放和旋转矫正,消除两幅原始影像之间的缩放和旋转变换,最后,再次对矫正后的影像使用相位相关法即可求出平移参数(x0,y0)。
2 分层Fourier-Mellin相位相关的初始视差获取方法
航空与遥感影像间不仅存在仿射畸变,还存在一定的透视畸变。基于 Fourier-Mellin变换的相位相关是在傅里叶变换和对数极坐标变换基础上的全局相位相关,可用于估计两幅影像之间大的平移位移,且对亮度变化不敏感,对噪声和遮挡等具有一定的鲁棒性,因此,也可用于获取具有仿射畸变与透视畸变的航空与航天遥感影像的初始视差。为了提高获取初始视差的效率、精度和鲁棒性,本文引入金字塔分层匹配思想,给出了分层Fourier-Mellin相位相关的影像匹配初始视差的全自动获取方法,具体过程如下。
1) 建立基准影像和待匹配影像的影像金字塔,分别对两幅影像的金字塔顶层影像进行傅里叶变换;
2) 将各自的幅度谱转换至对数极坐标下进行相位相关运算,求得两幅影像之间的旋转与缩放参数;
3) 利用旋转和缩放参数对待匹配影像进行旋转和缩放变形矫正;
4) 对金字塔顶层基准影像和矫正后的待匹配影像进行相位相关得到平移参数,计算出待匹配影像中心点的初始视差近似值;
5) 在金字塔的下一层影像上,分别选取待匹配影像中心点区域和基准影像上同样大小的同名区域进行相位相关运算;
6) 利用相关运算结果对初始视差近似值进行校正;
7) 重复步骤5)~6),直到影像原始层时结束,从而得到更精确的初始视差。
3 实验与分析
实验选用三组典型的原始立体影像对,尺寸均为1 024像素×1 024像素,图 1(a)与图 2(a)分别为具有重复纹理的较平坦地区的乡村与城市航空立体影像,图 3(a)为遮挡较严重的城市卫星立体影像。各图中左图均为基准影像,右图为待匹配影像,实验平台选择MATLAB2008。对上述三组立体影像分别进行分层FM相位相关匹配,计算待匹配影像中心点与其在基准影像上的同名点的初始视差,由初始视差可以计算基准影像上同名点的坐标,从而确定基准影像上同名点的位置。算法使用的影像金字塔共分3层,每层影像由两像素平均方式构建,最顶层金字塔影像的大小为256像素×256像素,对最顶层金字塔影像进行Fourier-Mellin变换相位相关,以下每层在上一层的视差约束下,使用分块相位相关,相关窗口大小为31像 素×31像素。实验结果如图 1(b)、图 2(b) 和图 3(b)所示。图 1(c)、图 2(c) 和图 3(c)为相应的局部放大影像。各图中右图为矫正后的待匹配影像图,白色十字交叉点(白色圆圈中心)为矫正后的待匹配影像的中心点;各图左图中的白色十字交叉点为矫正后的待匹配影像中心点经匹配后在基准影像中的同名点。实验还采用了Fourier-Mellin变换相位相关匹配法进行对比,同样计算待匹配影像中心点在基准影像上的同名点,相应的实验结果如图 1(d)、图 2(d) 和图 3(d)所示。表 1显示的是对上述三组立体影像分别使用Fourier-Mellin相位相关和分层Fourier-Mellin相位相关获取初始视差的误差及所需要的运算时间。

|
| 图 1 平坦地区遥感影像实验结果 Fig. 1 Experimental Result of Satellite Stereo Images of Flat Ares |

|
| 图 2 城市航空影像实验结果 Fig. 2 Experimental Result of Urban Aerial Stereo Image |

|
| 图 3 遮挡较严重的城市卫星影像实验结果 Fig. 3 Experimental Result of City Satellite Stereo Images with Obscured |
| 原始影像 | Fourier-Mellin法x、y方向视差误差/像素 | 分层FM法x、y方向视差误差/像素 | Fourier-Mellin运算耗时/s | 分层Fourier-Mellin运算耗时/s |
| 图 1(a) | (1,1) | (1,1) | 207.98 | 133.62 |
| 图 2(a) | (2,3) | (3,1) | 205.36 | 140.16 |
| 图 3(a) | (7,3) | (1,0) | 216.05 | 137.91 |
从实验结果可以看到,采用Fourier-Mellin相位相关运算获取图 1(a)、图 2(a) 和图 3(a) 立体影像对初始视差所用时间分别为207.98 s、205.36 s和216.05 s。图 1(a)立体影像对中心点的x、y方向的视差误差均为1个像素,图 2(a)立体影像对中心点的x、y方向的视差误差分别为2和3个像素,图 3(a) 立体影像对x和y方向的视差误差分别为7和3个像素。而采用分层Fourier-Mellin相位相关法获取图 1(a)、图 2(a) 和图 3(a) 立体影像对整体初始视差所用时间分别为133.62 s、140.16 s和137.91 s,效率明显高于Fourier-Mellin相位相关法。实验中,分层Fourier-Mellin相位相关法使用了三次线性插值法对影像进行矫正,矫正过程用时较长。若想缩短矫正过程的用时,可以改用双线性或最近邻插值法,进一步提高效率。分层FM相位相关法在精度上也明显高于Fourier-Mellin相位相关法。图 1(a)立体影像对中心点的x、y方向的视差误差均为1个像素,图 2(a)立体影像对中心点的x、y方向的视差误差分别为3个和1个像素,图 3(a) 立体影像对x和y方向的视差误差分别为1和0个像素,具体见表 1。图 3(a)是存在着遮挡现象的具有透视变换的立体影像对,使用分层FM相位相关算法获得立体影像对x和y方向的视差误差分别为1和0个像素,耗时137.91 s;而Fourier-Mellin相位相关法误差分别为7和3个像素,耗时216.05 s。由此可见,分层FM相位相关法获得的初始视差在精度和效率上均优于Fourier-Mellin相位相关法。
4 结 语
本文将Fourier-Mellin变换、相位相关与金字塔影像技术相结合,提出了分层Fourier-Mellin相位相关的影像匹配初始视差的全自动获取方法,并给出了具体的实现过程,以及相应的实验结果。几种典型地貌的航空和航天遥感立体影像匹配实验证明,本文提出的分层Fourier-Mellin相位相关算法均能获得影像中心点的误差在三个像素以内的初始视差,对于存在一定辐射畸变与几何畸变的影像同样能够获得其中心点较精确的初始视差。该方法无需任何辅助信息与先验知识,适用于航空和航天遥感影像的中心点的高精度初始视差的自动获取。
| [1] | Huang Yuqi, Mu Xiaohui, Qian Zengbo. Total-automatically Image Matching of Stereoscopic Pair of Aerial Photograpgy[J]. Journal of Institute of Surveying and Mapping, 2000, 17(4):277-283(黄玉琪, 牟晓辉, 钱曾波.航空摄影立体像对的全自动影像匹[J].测绘学院学报, 2000, 17(4):277-283) |
| [2] | Yuan Xiuxiao, Xu Ji, Xie Chou. An Algorithm for Determining Parallax of Aerial Images Based on Histograms od Edges and Grads[J].Geomatics and Information Science of Wuhan University, 2005, 30(9):762-765(袁修孝, 许骥, 谢酬.基于边缘梯度投影图的航空影像初始视差确定[J].武汉大学学报·信息科学版, 2005, 30(9):762-765) |
| [3] | Zhang Jianqing, Zhang Yong. Vertical Lines Supported Tie Points Auto Extraction of Large Scale Aerial Triangulation over Urban Areas[J]. Geomatics and Information Science of Wuhan University, 2008, 33(6):556-559(张剑清, 张勇.铅垂线辅助的大比例尺城区空三自动转点[J].武汉大学学报·信息科学版, 2008, 33(6):556-559) |
| [4] | Li Xiaoming, Zheng Lian, Hu Zhanyi. SIFT Based Automatic Registration of Remotely-sensed Imagery[J].Journal of Remote Sensing, 2006, 10(6):885-892(李晓明, 郑链, 胡占义.基于SIFT特征的遥感影像自动配准[J].遥感学报, 2006, 10(6):885-892) |
| [5] | Preddv B S, Challerji B N. An FFT-based Technique for Translation, Rotation, and Scale-invariant Image Registration [J]. IEEE Transactions on Image Processing, 1996, 5(8):1 266-1 271 |
| [6] | Li Xiaoming, Zhao Xunpo, Zheng Lian, et al. An Image Registration Technique Based on Fourier-Mellin Transform and Its Extended Applications[J].Chinese Journal of Computers, 2006, 29(3):466-472(李晓明, 赵训坡, 郑链, 等.基于Fourier-Mellin 变换的图像配准方法及应用拓展[J]. 计算机学报, 2006, 29(3):466-472) |
| [7] | Shi Xiaojin, Zhang Yunhua. A New Image Registration Method for Repeat-pass InSAR Based on Fourier-Mellin Transform and Correlation-Coefficient Algorithm[J].Journal of Electronics & Information Technology, 2009, 31(4):803-807(石晓进, 张云华.基于Fourier-Mellin 变换和相干系数法的重复轨道干涉SAR 图像配准新方法[J].电子与信息学报, 2009, 31(4):803-807) |
| [8] | Lin Hui, Liang Liang, Du Peijun, et al. Image Registration Based on Fourier-Meliin Transform[J]. Geomatics and Information Science of Wuhan University, 2012, 37(6):649-652(林卉, 梁亮, 杜培军, 等.利用Fourier-Mellin变换的遥感图像自动配准[J].武汉大学学报·信息科学版), 2012, 37(6):649-652) |
| [9] | Kuglin C D, Hines D C. The Phase Correlation Image Alignment Method[C]. IEEE International Conference on Cybernetics and Society, New York, 1975 |
| [10] | Chen Q, Defrise M F. Symmetric Phase-only Matched Filtering of Fourier-Mellin Transform for Image Registration and Recognition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1994, 16(12):1 156-1 168 |
 2015, Vol. 40
2015, Vol. 40


