文章信息
- 柯宝贵, 章传银, 郭春喜, 王斌, 杨磊
- KE Baogui, ZHANG Chuanyin, GUO Chunxi, WANG Bin, YANG Lei
- 船载重力测量数据不同测区系统偏差纠正方法研究
- System Error Correction for Shipborne Gravimetric Data form Different Regions of Offshore in China
- 武汉大学学报·信息科学版, 2015, 40(3): 417-421
- Geomatics and Information Science of Wuhan University, 2015, 40(3): 417-421
- http://dx.doi.org/10.13203/j.whugis20130299
-
文章历史
- 收稿日期:2014-07-04
2. 国家测绘地理信息局大地测量数据处理中心, 陕西 西安, 710054;
3. 国家海洋局第一海洋研究所, 山东 青岛, 266061
2. Geodetic Data Processing Center, State Bureau of Surveying and Mapping, Xi'an 710054, China;
3. First Institute of Oceanography, State Oceanic Administration, Qingdao 266061, China
海洋重力数据在建立全球或区域陆海统一的高程基准[1]、反演地壳深部结构[2] 、地质地球物理勘探以及航天和远程武器的发射等方面有着广泛应用[3]。船载重力测量数据是海洋重力数据的重要组成部分[4, 5, 6],消除不同部门、不同时期所提供测量数据之间的基准不一致性,发挥已有实测数据的价值,满足科研、生产的需求具有重要科学意义。船载重力测量通常以测线的形式施测,主要由主副测线相交(直交或斜交)构成测线网。主副测线相交得到的交叉点不符值是分析研究海洋测量观测质量的关键参数。目前,关于船载重力测量测线交叉点不符值主要用来确定同一个测区的系统误差或修正定位误差,或基于秩亏网平差理论, 利用测线网加权秩亏网平差模型,探讨测线系统误差的调整方案[ 7, 8, 9, 10 ]。类似的航空重力测量测线数据处理方法有较多讨论[11, 12],但均缺少对不同测区之间存在系统偏差时对测线数据进行纠正的研究。本文利用高精度重力场模型能反映真实地球重力场趋势性的中长波分量的特征[13],提出了消除不同测区之间重力测线上重力异常存在系统偏差的方案;并提出了基于参考线,利用参考测线上交叉点处的残差重力异常不符值,纠正其他测线重力异常的新思路。结果表明,利用本文方法纠正后,不同测区的重力值不存在系统偏差,交叉点处的不符值明显改善,测线上的纠正后重力异常明显优于纠正前的重力异常。 1 重力数据 1.1 我国近海海域船载重力测量数据
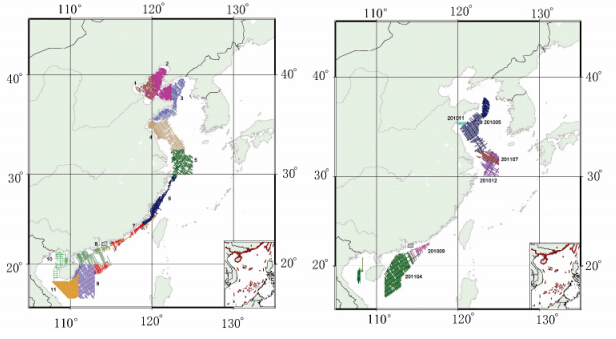
根据收集到的数据,我国近海海域船载重力测量数据分为17个测区,不同测区由不同部门或单位施测,存在数据格式不一致、基准不统一的问题。因201107测区只有主测线,没有副测线,不存在交叉点以供检核,关于该区的处理方案不在本文的研究范围内。本文仅研究其他16个测区的数据处理方法,各测区分布如图 1所示。为了明确标示不同测区,避免因测区重合而导致混淆,故将我国近海船载重力测量区域分成两幅图。
由于各种原因,在测区之间有重叠区域,不同测区空间重力异常明显存在系统偏差。即在图 1中所示的各个测区中,有相互重合观测数据的测区之间,相邻测区的重力异常数据过渡不平滑,存在台阶装的突跳,部分区域变化高达30 mGal。
|
| 图 1 我国近海海域船载重力数据区域分布(不同颜色表示不同测区与数据来源) Fig. 1 Gravimetric Data Distribution in China Offshore,Different Color to Show Difference Coastal Data Region |
部分测区内测线间的重力场变化趋势也存在矛盾。即不同测线两端在重合观测范围内时,不同航次的测线数据变化趋势有波纹状的起伏。
因为数据存在着上述种种不利因素,严重阻碍了船载重力测量数据在大地测量与海洋地质调查方面的应用,制约着有关岛礁资源的开发利用。 1.2 高阶地球重力场模型
本文选择1 420阶的全球重力模型eigen-6c[14] 计算测线观测点上重力异常,该模型由ICGEM(International Center for Global Gravity Field Models)研制而成,相比于EGM2008的2 190阶,其优势在于采用了GOCE卫星重力梯度数据,可直接反映出重力位水准面的曲率与力线弯曲及地球重力场的精细结构。本文将利用eigen-6c重力场模型计算我国近海海域船载重力测线处的模型重力异常[15]。
2 船载重力测量数据的纠正
为了消除船载测量重力数据不同测区间存在的系统偏差以及测区内数据基准不统一的问题,从而精化船测重力数据,提高数据质量,采用了如下步骤进行纠正。
1) 计算模型重力异常。由高精度的卫星重力场模型eigen-6c,其阶次高达1 420,在我国近海海域的船载重力测量观测点处计算得到。
2) 计算测点重力异常。将船载测量各测线上的绝对重力值,转换为重力异常。
3) 计算测线上的残差重力异常。由实测重力异常与模型重力异常相减得到。在残差重力异常中扣除实测重力异常与模型重力异常之间的系统偏差,即可统一各测区的基准,使之不存在系统偏差。
4) 利用测线上的残差重力异常,计算主副测线交叉点处的不符值。此处理方式可突出测线交叉点的重力场局部变化特征。
5) 选择参考测线。对各测线的残差重力异常进行统计,挑选平均值与标准差尽可能地小、测线上实际观测点尽可能多、不符值满足船载重力测量规范限差要求、测线交叉点尽可能多的测线作为参考测线[16, 17]。这种方法所选择的参考线,一方面能与测区的其他观测数据变化趋势一致;另一方面,能较客观地反映实际数据特征。选择参考测线的方法不同于以往测线网加权秩亏网平差模型,需要人为地添加其他约束条件。
6) 测线观测值纠正。以参考测线为基准,即在观测值纠正的过程中,参考测线上的观测值保持不变。利用参考测线上交叉点不符值,纠正其他非参考测线观测值[10]。
基于上述步骤,统一了不同区域船载重力测量数据的基准,消除了区域之间的系统偏差,并可平滑过渡,增强了测区之间数据的一致性。
3 纠正后的船载重力测量数据比较分析 3.1 纠正后重力异常与eigen-6c残差对比
按照船载重力测量数据的纠正计算步骤,对我国近海海域的船载重力测量数据进行了纠正,与eigen-6c模型的重力异常残差统计结果见表 1。经纠正后,各测区已无明显的系统偏差,标准差较纠正前的结果有较大程度的改善。
| 测区编号 | 最大值 | 最小值 | 平均值 | 标准差 | |
| 1 | 纠正前 | 32.810 | -21.225 | 3.760 | 8.811 |
| 纠正后 | 23.033 | -37.027 | 0.042 | 4.994 | |
| 2 | 纠正前 | 52.497 | -15.308 | 13.985 | 9.877 |
| 纠正后 | 27.333 | -26.783 | -0.034 | 6.697 | |
| 3 | 纠正前 | 35.749 | -23.383 | 6.694 | 9.522 |
| 纠正后 | 28.413 | -19.680 | -0.026 | 5.576 | |
| 4 | 纠正前 | 28.952 | -26.051 | 5.918 | 7.663 |
| 纠正后 | 29.528 | -25.844 | 0.072 | 4.928 | |
| 5 | 纠正前 | 16.064 | -29.523 | -7.809 | 6.344 |
| 纠正后 | 15.781 | -26.560 | -0.197 | 3.806 | |
| 6 | 纠正前 | 56.021 | -16.872 | 15.468 | 11.150 |
| 纠正后 | 36.114 | -27.715 | -0.061 | 8.021 | |
| 7 | 纠正前 | 42.318 | -33.197 | 7.663 | 11.241 |
| 纠正后 | 33.481 | -25.300 | -0.224 | 7.198 | |
| 8 | 纠正前 | 36.781 | -23.927 | 8.560 | 8.245 |
| 纠正后 | 32.459 | -26.130 | 1.015 | 6.220 | |
| 9 | 纠正前 | 80.402 | -28.435 | 7.520 | 13.498 |
| 纠正后 | 43.529 | -34.158 | 0.102 | 5.419 | |
| 10 | 纠正前 | 37.274 | -13.188 | 11.477 | 7.986 |
| 纠正后 | 25.830 | -34.949 | -1.662 | 6.985 | |
| 11 | 纠正前 | 66.729 | -19.960 | 15.098 | 12.456 |
| 纠正后 | 23.948 | -21.123 | 1.189 | 5.156 | |
| 201005 | 纠正前 | 35.321 | -33.740 | 4.788 | 9.128 |
| 纠正后 | 46.707 | -40.785 | -0.042 | 4.188 | |
| 201009 | 纠正前 | 30.255 | -8.327 | 7.914 | 5.825 |
| 纠正后 | 10.521 | -9.718 | -0.116 | 2.889 | |
| 201011 | 纠正前 | 31.316 | -6.552 | 12.518 | 7.314 |
| 纠正后 | 13.700 | -19.840 | -1.274 | 8.207 | |
| 201012 | 纠正前 | 47.055 | -46.672 | -6.495 | 8.192 |
| 纠正后 | 82.795 | -66.072 | 0.046 | 5.023 | |
| 201104 | 纠正前 | 54.438 | -23.759 | 8.505 | 10.659 |
| 纠正后 | 38.710 | -20.257 | -0.097 | 4.828 | |
为了进一步检验船载重力测量的数据处理质量,比较了数据处理前后,各区交叉点不符值变化,见表 2。从表 2中可以看出,经过纠正后的交叉点不符值明显优于纠正前的不符值。
| 测区编号 | 最大值 | 最小值 | 平均值 | 标准差 | |
| 1 | 纠正前 | 5.415 | -5.940 | -0.060 | 1.842 |
| 纠正后 | 0.965 | -2.068 | -0.022 | 0.308 | |
| 2 | 纠正前 | 4.516 | -2.684 | -0.025 | 0.960 |
| 纠正后 | 1.811 | -1.055 | 0.003 | 0.220 | |
| 3 | 纠正前 | 5.781 | -5.126 | -0.086 | 2.030 |
| 纠正后 | 2.190 | -1.856 | -0.001 | 0.513 | |
| 4 | 纠正前 | 3.704 | -3.931 | 0.039 | 1.367 |
| 纠正后 | 1.720 | -1.143 | 0.012 | 0.317 | |
| 5 | 纠正前 | 4.468 | -4.911 | -0.116 | 1.788 |
| 纠正后 | 1.409 | -1.167 | -0.016 | 0.280 | |
| 6 | 纠正前 | 5.083 | -4.814 | -0.011 | 1.720 |
| 纠正后 | 2.408 | -2.086 | 0.004 | 0.406 | |
| 7 | 纠正前 | 7.461 | -6.290 | 0.017 | 2.683 |
| 纠正后 | 2.376 | -2.325 | -0.012 | 0.839 | |
| 8 | 纠正前 | 5.086 | -4.976 | -0.283 | 2.645 |
| 纠正后 | 2.543 | -2.264 | 0.006 | 0.786 | |
| 9 | 纠正前 | 5.840 | -6.942 | 0.026 | 1.883 |
| 纠正后 | 1.453 | -1.252 | 0.000 | 0.275 | |
| 10 | 纠正前 | 2.087 | -4.664 | 0.108 | 1.006 |
| 纠正后 | 0.984 | -0.736 | 0.032 | 0.300 | |
| 11 | 纠正前 | 22.583 | -13.129 | 0.122 | 3.394 |
| 纠正后 | 2.273 | -2.339 | -0.002 | 0.263 | |
| 201005 | 纠正前 | 4.254 | -4.324 | 0.053 | 1.378 |
| 纠正后 | 0.968 | -1.131 | 0.021 | 0.258 | |
| 201009 | 纠正前 | 1.442 | -4.223 | -0.272 | 1.175 |
| 纠正后 | 0.102 | -0.044 | 0.006 | 0.030 | |
| 201011 | 纠正前 | 6.100 | -0.850 | 3.229 | 2.965 |
| 纠正后 | 1.750 | -0.425 | 0.008 | 0.559 | |
| 201012 | 纠正前 | 10.045 | -5.232 | 0.411 | 3.433 |
| 纠正后 | 1.680 | -1.815 | 0.030 | 0.659 | |
| 201104 | 纠正前 | 6.750 | -6.600 | -0.119 | 2.371 |
| 纠正后 | 1.309 | -1.498 | -0.004 | 0.269 | |
本文利用高精度高阶重力场模型能反映真实 地球重力场变化趋势的优势,从我国近海海域船载重力测量数据中扣除模型重力异常分量,利用残差重力异常消除不同测区间的系统偏差;以尽可能最大程度地符合数据实际情况的标准来选择参考测线,克服加权秩亏网平差模型需要人为地添加其他约束条件的不足,进行我国近海海域的船载重力测量重力值纠正的工作,纠正后的成果质量明显优于纠正前的成果质量。基于参考测线纠正其他非参考测线的方法,不仅可直接应用于海洋重磁测量、水深测量、卫星测高沿轨及航空重力测线等方面的数据处理,其原则也同样适用于其他需要用重复观测方法来评定资料质量的技术领域。
| [1] | Guan Zelin, Guan Zheng, Zhai Guojun.Sea Surface Topography and Altitude Datum[M].Beijing:Publishing House of Surveying and Mapping, 1996(管泽霖, 管铮, 翟国君.海面地形与高程基准[M].北京:测绘出版社, 1996) |
| [2] | Chao Dingbo, Yao Yunsheng, Li Jiancheng, et al. Interpretaion on the Tectonics and Characteristics of Altimeter-derived Gravity Anomalies in China South Sea[J].Geomatics and Information Science of Wuhan University, 2002, 27(4):343-347(晁定波, 姚运生, 李建成, 等.南海海盆测高重力异常特征及构造解释[J].武汉大学学报\5信息科学版, 2002, 27(4):343-347) |
| [3] | Huang Motao, Zhai Guojun, Guan Zheng, et al. Determination and Application of Marine Gravity Field[M].Beijing:Surveying and Mapping Press, 2005(黄谟涛, 翟国君, 管铮, 等. 海洋重力场测定及其应用[M].北京:测绘出版社, 2005) |
| [4] | Li Jiancheng, Ning Jinsheng, Chen Junyong, et al. Determination of Gravity Anomalies over the South China Sea by Combination of TOPEX/Poseidon, ERS2 and Geosat Altimeter Data[J].Acta Geodaetcaet Cartographica Sinica, 2001, 30(3):197-202(李建成, 宁津生, 陈俊勇, 等.联合TOPEX/Poseidon, ERS2和Geosat卫星测高资料确定中国近海重力异常[J].测绘学报, 2001, 30(3):197-202) |
| [5] | Hwang C. Inverse Vening Meinesz Formula and Deflection-geoid Formula:Applications to the Predictions of Gravity and Geoid over the South China Sea[J].Journal of Geodesy, 1998, 72:304-312 |
| [6] | Wang Haiying, Wang Guangyun. Inversion of Gravity Anomalies from Along-track Vertical Deflections with Satellite Altimeter Data and Its Applications[J].Acta Geodaetcaet Cartographica Sinica, 2001, 30(1):21-26(王海瑛, 王广运. 卫星测高数据的沿轨迹重力异常反演法及其应用[J].测绘学报, 2001, 30(1):21-26) |
| [7] | Huang Motao. Examniation, Adjustment and Precision Estimation of Half-Systematic Error in Marine Gravity Surveying[J].Marine Science Bulletin, 1990, 9(4):81-86(黄谟涛.海洋重力测量半系统差检验、调整及精度计算[J].海洋通报, 1990, 9(4):81-86) |
| [8] | Huang Motao. Marine Gravity Survey Line Network Adjustment[J].Acta Geodaetca et Cartographica Sinica, 1993, 22(2):103-110(黄谟涛. 海洋重力测线网平差[J].测绘学报, 1993, 22(2):103-110) |
| [9] | Liu Yanchun, Li Mingsan, Huang Motao. The Rank_Defect Adjustment Model for Survey-line Systematic Errors in Marine Survey Net[J].Geomatics and Information Science of Wuhan University, 2012, 26(6):533-538(刘雁春, 李明叁, 黄谟涛. 海洋测线网系统误差调整的秩亏网平差模型[J].武汉大学学报\5信息科学版, 2012, 26(6):533-538) |
| [10] | Li Mingsan, Liu Yanchun, Huang Motao, et al. Three Models for Determination of Survey-line Systematic Errors in Marine Survey Net[J].Journal of Institute of Surveying and Mapping, 2002, 19(3):157-161(李明叁, 刘雁春, 黄谟涛, 等.海洋测线网系统误差确定的3种模型[J].测绘学院学报, 2002, 19(3):157-161) |
| [11] | Li Hai.Theory and Methods of Network Adjustment of Airborne Gravimetry[D].Zhengzhou:Information Engineering University, 2002(李海.航空重力测量测线网平差的理论与方法[D].郑州:信息工程大学, 2002) |
| [12] | Cai Shaokun. Research on the Network Adjustment of Airborne Gravimetry[D].Changsha:National University of Defense Technology, 2009(蔡劭琨.航空重力测量网络平差方法研究[D].长沙:国防科学技术大学, 2009) |
| [13] | Zhang Chuanyin, Guo Chunxi, Chen Junyong, et al.EGM2008 and Its Application Analysis in Chinese Mainlad[J].Acta Geodaetcaet Carto graphica Sinica, 2009, 38(4):283-289(章传银, 郭春喜, 陈俊勇, 等.EGM 2008地球重力场模型在中国大陆适用性分析[J].测绘学报, 2009, 38(4):283-289) |
| [14] | Foerste C, Bruinsma S, Shako R, et al. EIGEN-6--A New Combined Global Gravity Field Model Including GOCE Data from the Collaboration of GFZ-Potsdam and GRGS-Toulouse[R]. Geophysical Research Abstracts, Vol.13, EGU2011-3242-2, EGU General Assembly, 2011 |
| [15] | Li Jiancheng, Chen Junyong, Ning Jinsheng. Earth's Gravity Field Approximation Theory and China's 2000 Quasi-geoid Determination[M].Wuhan:Wuhan University Press, 2003(李建成, 陈俊勇, 宁津生. 地球重力场逼近理论与中国2000似大地水准面的确定[M].武汉:武汉大学出版社, 2003) |
| [16] | Zhou Jiangwen.Classical Theory of Error and Robust Estimation[J].Acta Geodaetica et Carto-graphica Sinica, 1989, 18(2):115-120(周江文.经典误差理论与抗差估计[J].测绘学报, 1989, 18(2):115-120) |
| [17] | Deng Kailiang, Bao Jingyang, Zhang Chuanyin, et al. The Determination of Quasi Stationary Sea Surface Topography over China Sea by Using Multialtimeter Data[J].Acta Geoda etica et Cartographica Sinica, 2009, 38(2):114-119(邓凯亮, 暴景阳, 章传银, 等. 联合多代卫星测高数据确定中国近海稳态海面地形模型[J].测绘学报, 2009, 38(2):114-119) |
 2015, Vol. 40
2015, Vol. 40


