文章信息
- 李凯锋, 欧阳永忠, 陆秀平, 徐卫明
- LI Kaifeng, OUYANG Yongzhong, LU Xiuping, XU Weiming
- 基于PPP技术的海岛礁平面控制测量应用实践
- Application of Precise Point Positioning for Island Control Survey
- 武汉大学学报·信息科学版, 2015, 40(3): 412-416
- Geomatics and Information Science of Wuhan University, 2015, 40(3): 412-416
- http://dx.doi.org/10.13203/j.whugis20130177
-
文章历史
- 收稿日期:2013-06-03
2. 武汉大学测绘学院, 湖北 武汉, 430072;
3. 大连舰艇学院海测工程系, 辽宁 大连, 116018
2. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China;
3. Department of Hydrography and Cartography, Dalian Naval Academy, Dalian 116018, China
目前,经典控制测量中一般采用GPS静态测量技术—组网观测模式建立GPS控制网,进行静态基线处理和网平差[1, 2, 3, 4] ,通过与已知点的坐标联测,得到未知点的坐标。为了保证静态基线解算的可靠性和精度,在进行控制测量时,仍然要求测区有一定密度的已知高等级大地控制点。这对于大范围的沿岸控制测量任务来讲,将大大增加人力、物力和财力的投入,特别是我国是海洋大国,沿海一带地形复杂,布设一定密度的控制网具有相当的难度,有些测区附近已知控制点与测区的未知点组成的控制网网形不规则;有些测区附近已知控制点数量根本就不够,无法组成规则的、有效的GPS控制网。此外,对于一些远离大陆的岛礁,测区及附近没有高等级大地控制点,经典控制测量方法无法实施。随着IGS 轨道产品和钟差产品精度的不断提高(目前,IGS事后轨道精度已优于3 cm,钟的精度优于0.1 ns),精密单点定位PPP技术越来越得到人们的重视,为沿岸及海岛礁进行高等级平面控制测量提供了新的解决方案。
本文利用开发的软件系统(HPPP)将PPP用于海岛礁平面控制测量领域,用实测的GPS 静态数据进行静态精密单点定位的解算,在不使用已知控制点的条件下,获得了与组网观测模式进行相对静态定位相当的精度。
1 精密单点定位
精密单点定位技术[5, 6]以单台双频GPS接收机采集的相位和伪距数据作为主要观测值,通过利用IGS提供的精密星历和卫星钟差,加上精确的误差改正模型,其定位精度可达dm级甚至cm级。PPP定位模型比较常见的有传统模型、UofC模型和无模糊度模型等3种[7, 8],3种模型的主要区别在于载波相位中模糊度的处理方式不同。其中UofC模型不仅能够消除一阶电离层影响,而且还降低了组合观测值的噪声水平,另外,还加快模糊度解算收敛速度[7]。其观测模型如下:
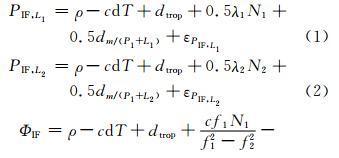
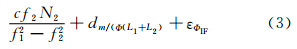
式中,PIF,L1、PIF,L2分别为L1和L2两个频率上码与相位的组合观测值;ΦIF为L1和L2两个频率无电层相位组合观测值;ρ为卫星至接收机的几何距离;c为真空中光的速度;dT为GPS卫星钟差;dtrop为对流层延迟;f1、f2分别为载波L1和L2的频率; N1、N2分别为L1和L2上载波相位的整周模糊度;dm为多路径效应;ε为观测值的噪声和未被模型化的误差。
将PIF,L1、PIF,L2和ΦIF作为观测值,测站坐标、接收机钟差、无电离层组合模糊度、多路径效应和对流层延迟做为未知参数,然后对参数进行估计,解算出所有参数的估值。
2 试验验证 2.1 静态精密单点定位精度验证
本文分别从观测数据时段长度和数据采样间隔两个方面分析自主开发的精密单点定位软件静态解算精度及收敛情况。其解算结果与GrafNav PPP模块和加拿大的CSRS-PPP软件解算结果进行比较。观测数据选用IGS跟踪站及利用NovAtel双频GPS接收机自主采集的静态数据。具体验证方法如下。
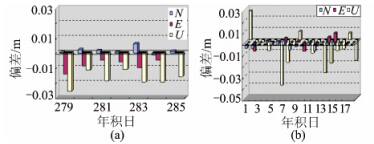
利用IGS最终精密星历和精密钟差,使用开发的软件进行PPP解算,得到测站坐标(XYZ/BLH),并将其转换至NEU方向,与ITRF参考框架下的真值比较结果如图 1,图中横轴代表年积日,纵轴为偏差值,单位为m(下同)。
|
| 图 1 PPP单天解精度 Fig. 1 Static PPP Accuracy of Day Results |
图 1(a)为BJFS站软件单天解坐标时间序列同IGS真实坐标之间的差异;图 1(b)为18个IGS跟踪站的软件单天解偏差均值统计。几乎所有跟踪站的PPP单天解在平面方向的精度为mm级,高程方向的精度为2~3 cm。少数测站的定位误差偏大,达到5~6 cm。 2.2 采样率对收敛时间的影响分析
为了分析在不同采样率情况下静态PPP的收敛时间以及所能达到的精度状况,选取南海某海岛测区进行静态精密单点试验的观测数据,使用开发的软件进行PPP解算并与Gamit软件网解的结果进行比较,如表 1所示。
| 采样率/s | 较差/cm | 收敛时间/s | ||
| N | E | U | ||
| 1 | 0.9 | -1.5 | -0.7 | 4 950 |
| 5 | 0.9 | -1.5 | -0.5 | 4 950 |
| 10 | 0.8 | -1.5 | -0.4 | 4 950 |
| 15 | 0.8 | -1.5 | -0.3 | 4 950 |
| 30 | 0.7 | -1.5 | -0.3 | 4 950 |
| 45 | 0.7 | -1.5 | 0.1 | 4 950 |
| 60 | 1.0 | -1.6 | 0.6 | 5 010 |
由表 1可知,不同采样率的收敛时间几乎相同,但解算的坐标值有变化,与网解坐标值相比较,纬度方向差别很小,经度和高程方向的值发生微小变化,数据采样间隔为60 s时,纬度方向差值最大达到-1.6 cm,收敛时间稍长一些,所以采样率不宜过大。
2.3 采样率的确定
由于下载的各个IGS跟踪站数据采样率都为30 s,为分析采样率对静态PPP精度的影响,从IGS跟踪站下载的数据不能满足实验要求,因此,我们采用NovAtel双频GPS接收机,对固定的未知坐标点进行连续观测(图 2)。选取 时间为2009年年积日自40至53(对应为2009-02-09~02-22)为期两周的观测数据,数据采样间隔为0.05 s,从观测文件中提取1 s、5 s、10 s、15 s、30 s等5组采样率的观测数据,利用IGS最终精密星历和精密 钟差,使用开发的软件HPPP和GrafNav8.3分别进行精密单点定位解算,将得到的测站坐标(XYZ/BLH)与GrafNav8.30的解进行比较作差,以便从平面与高程方向进行分析。
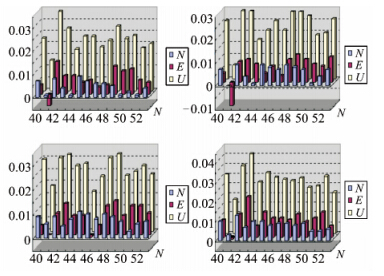
|
| 图 2 不同采样率对解算精度的影响 Fig. 2 Effects of Accuracy with Different Intervals |
图 2反映了不同采样率对应的静态PPP解算精度,因为本项目软件与GrafNavPPP模块在算法和模型上有区别,所以存在一定的系统误差是难免的。通过上述同一时段不同采样率的数据静态PPP解的比较,可见采样率为1 s~5 s时比较适合用于双频GPS静态精密单点定位。
2.4 观测时段长度对定位精度的影响
为了分析在不同的观测时段长度情况下静态精密单点定位所能达到的精度状况,我们依次选取IGS跟踪站-bjfs站的若干组观测时间长度依次为24、12、6、4、2和1 h的观测数据进行PPP解算。图 3反映了不同长度观测时段对应的静态PPP解算精度,在实际应用中用户可以根据精度的要求合理设计必要的观测时段长度。

|
| 图 3 观测时段长度的解算精度时间序列 Fig. 3 Accuracy of Positioning Using Different Time Length of Observation Data |
图 3反映了不同长度观测时段对应的静态PPP解算精度,观测1 h在平面方向与高程方向均优于1 dm。观测2 h平面精度达到1~2 cm,高程方向为3~4 cm,点位误差优于5 cm。观测4 h平面精度为1 cm左右,高程方向为2 cm左右,点位误差优于3 cm。观测6 h平面精度为几个mm,高程方向为1 cm左右,点位误差优于2 cm。观测时间延长至12 h,其定位精度与6 h解结果基本一致。当观测时间延长至24 h,平面与高程方向的定位精度收敛至3~5 mm,点位误差优于1 cm。
3 PPP技术用于沿岸及岛礁控制测量 3.1 PPP控制测量作业方案
当所测区域没有已知点或已知点不够时,根据上述试验验证,结合海岛礁测绘的工程实际,PPP进行海岛礁控制测量作业的方案如下:
1) 根据测图精度要求,确定首级控制测量的观测时段长度;
2) 根据不同采样率对解算精度的影响分析,选择数据采样率;
3) 利用IGS最终精密星历和精密钟差,进行PPP解算;
4) 采用PPP解算的首级控制测量成果,进行组网观测,逐级发展控制点。
3.2 沿岸控制测量
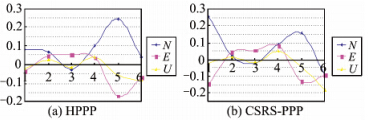
为验证PPP技术在静态控制测量作业中的可行性,在沿岸某测区进行静态精密单点试验。测区一共6个控制点,4个国家C级GPS控制点,一个海控I级控制点和一个海控II级控制点。利用双频GPS接收机进行观测,观测时段长度为1 h,数据采样间隔为15 s,利用IGS最终精密星历和精密钟差,使用开发的软件进行PPP解算,同时也将观测数据用加拿大的CSRS-PPP软件进行解算,将得到的测站坐标(XYZ/BLH)与已知控制点坐标进行比较,结果图 4所示。
|
| 图 4 PPP应用于沿岸控制测量精度 Fig. 4 Static PPP Accuracy of Positioning in Coastwise Control Survey |
图 4(a)为HPPP解坐标同已知坐标之间的差值,图 4(b)为CSRS-PPP解坐标同已知坐标之间的差值。由两图 4可知,PPP连续1 h观测值解的精度大部分都在1 dm以内,与软件CSRS-PPP解的精度相当。
3.3 岛礁控制测量
首先利用IGS跟踪站(SHAO、TWTF、PIMO、KUNM、CUSV)与某海岛测区待求的两个未知控制点(DJST、DTSX)组成控制网,一共观测6个时段,每个时段长度为9 h,数据采样间隔为5 s,利用IGS最终精密星历和精密钟差,采用Gamit软件进行解算,并用GLOBK进行网平差计算,控制网如图 5。

|
| 图 5 某岛礁控制测量网 Fig. 5 Chart of Geodetic Network |
由表 2可知,9 h解单点定位解与网解的差值在2 cm以内,从而说明静态PPP能够用于高精度海岛礁平面控制测量。
| 点名 | RMS/cm | 与网解差值/cm | ||||
| X | Y | Z | X | Y | Z | |
| DJST | 0. 02 | 0.02 | 0.08 | -1.54 | 1.59 | -0.88 |
| DTSX | 0.04 | 0.04 | 0.15 | -1.86 | 1.92 | -0.42 |
PPP解算的坐标是基于下载的精密星历的参考框架(如IGS08),历元为观测值时间,而我国从2008-07-01启用的2000国家大地坐标(CGCS2000)参考框架为ITRF97[9, 10],参考历元为2000.0。要将PPP的解算坐标转换到2000国家大地坐标,需要经过历元变换、坐标变换和速度变换。基于PPP的海岛礁平面控制测量坐标转换有以下两种情况:
1) 当海岛礁周围有高等级控制点(已知2000国家大地坐标,且点数在3个以上)时,求取公共转换参数,再将PPP的解算坐标转换到2000国家大地坐标;
2) 当所测区域没有已知点或已知点不够时,首先需要进行参考框架的转换(如ITRF08- ITRF97),然后根据待求点所处板块,以及周围IGS站的分布情况,得到待求点的站度,经过速度变换得到2000国家大地坐标。
4 结 语
本文结果表明,精密单点定位可以实现cm级静态定位,能在不需要建立控制网的条件下达到基线网平差解相当的精度水平,将PPP技术应用于海控级控制点的测量,因为该方法无需进行联测,在没有高精度已知控制点时能够得到高精度的ITRF框架坐标,同时为海岛与大陆地区建立和维持高精度的坐标框架提供了新的技术手段。当然,PPP并不能取代传统的高精度相对定位,两者各有优势,如果所有模型处理正确,相对定位和PPP的结果应该是一致的。PPP中使用IGS 数据处理中心发布的精密星历和卫星钟差产品,在充分考虑了所有的不能忽略的误差模型改正,且软件算法正确的前提下,PPP的精度和可靠性在很大程度上取决于IGS产品的可靠性和精度[11, 12, 13, 14]。因此,IGS产品的质量分析是今后需要进一步研究的问题。
致谢:感谢麻省理工学院提供的GAMIT/GLOBK软件,以及IGS分析中心提供的数据和相关产品。
| [1] | Lv Zhiping, Qiao Shubo.Foundation of Geodesy[M].Beijing:The Publishing House of Surveying and Maping, 2010:37-45(吕志平, 乔书波.大地测量学基础[M].北京:测绘出版社, 2010:37-45) |
| [2] | Shi Yimin.Contemporary Geodetic Control Survey[M].Beijing:The Publishing House of Surveying and Maping, 2008:147-160(施一民.现代大地控制测量[M].北京:测绘出版社, 2008:147-160) |
| [3] | Li Yanxing, Hu Xinkang, Zhao Chengkun.The Research of Data Processing Method in GPS Monitor Network[J].Acta Geodaetica et Cartographica Sinica, 1999, 38(1):62-66(李延兴, 胡新康, 赵承坤.GPS监测网数据处理方案研究[J].测绘学报, 1999, 38(1):62-66) |
| [4] | Cheng Pengfei, Yang Yuanxi, Li Jiancheng.The Latest Advances in Geodesy[J].Bulletin of Surveying and Mapping, 2007(2):1-4(程鹏飞, 杨元喜, 李建成, 等.我国大地测量及卫星导航定位技术的新进展[J].测绘通报, 2007(2):1-4) |
| [5] | Ye Shirong, Zhang Shuangcheng, Liu Jingnan.Precision Analysis of Precise Point Positioning Based Tropospheric Delay Estimation[J].Geomatics and Information Science of Wuhan University, 2008, 33(8):788-791(叶世榕, 张双成, 刘经南.精密单点定位方法估计对流层延迟精度分析[J].武汉大学学报·信息科学版, 2008, 33(8):788-791) |
| [6] | Zhang Xiaohong, Liu Jingnan, Forsberg R.Application of Precise Point Positioning in Airborne Survey[J].Geomatics and Information Science of Wuhan University, 2006, 31(1):19-22(张小红, 刘经南, Forsberg R.基于精密单点定位技术的航空测量应用实践[J].武汉大学学报·信息科学版, 2006, 31(1):19-22) |
| [7] | Li Kaifeng, Ouyang Yongzhong, Lu Xiuping, et al.Hydrographic Surveying Based on GPS Precise Point Positioning[J].Hydrographic Surveying and Charting, 2009(1):1-4(李凯锋, 欧阳永忠, 陆秀平, 等.基于GPS精密单点定位技术的水深测量[J].海洋测绘, 2009(1):1-4) |
| [8] | Ye Shirong.Precise Point Positioning Based on Undifferenced GPS Data[D].Wuhan:Wuhan University, 2002(叶世榕.GPS非差相位精密单点定位理论与实现[D].武汉:武汉大学, 2002) |
| [9] | Dong Chaoyang, Xu Sida.Analysis of GPS Geodetic Control Network Layout for Boundary Survey[J].Hydrographic Surveying and Charting, 2010(2):64-66(董朝阳, 徐思达.边界测量GPS大地控制网布设分析[J].海洋测绘, 2010(2):64-66) |
| [10] | Tang Yingzhe, Yang Yuanxi, Song Xiaoyong.Data Processing and Result of National 2000' GPS Geodetic Control Network[J].Journal of Geodesy and Geodynamics, 2003(3):77-80(唐颖哲, 杨元喜, 宋小勇.2000国家GPS大地控制网数据处理方法与结果[J].大地测量与地球动力学, 2003(3):77-80) |
| [11] | Reha D, Alkan M.Hydrographic Surveying with a Tide Gauge[J].International Hydrographic Review, 2001, 2(1):69-79 |
| [12] | Abdel-salam M A.Precise Point Positioning Un-Differenced Code and Carrier Phase Observations[D].Calgary, Alberta, Canada:the University of Calgary, 2005 |
| [13] | Witchayangkoon B.Elements of GPS Precise Point Positioning[D].Orono, Maine:University of Maine, 2000 |
| [14] | Hobiger T, Ichikawa R.Ray-traced Troposphere Slant Delays for Precise Point Positioning[J].Earth Planets Space, 2008, 60(1):1-4 |
 2015, Vol. 40
2015, Vol. 40


