文章信息
- 朱银兵, 李豹, 刘睿
- ZHU Yinbing, LI Bao, LIU Rui
- BOC信号改进码相位捕获算法研究
- An Improved Code Phase Acquisition Algorithm for BOC Signal
- 武汉大学学报·信息科学版, 2015, 40(3): 406-411
- Geomatics and Information Science of Wuhan University, 2015, 40(3): 406-411
- http://dx.doi.org/10.13203/j.whugis20130268
-
文章历史
- 收稿日期:2013-06-19
随着技术的发展,全球卫星导航系统进入了一个新的发展时期。在导航信号的设计上,BOC调制已成为当前的研究热点。大量学者对BOC调制[1, 2, 3]进行了研究;并对BOC调制,尤其是BOC(1,1)调制信号的捕获方法[4]展开了研究,具体的捕获方法有峰跳法、早迟相关器技术、类BPSK方法[5, 6, 7, 8]、副峰消除技术[8, 9, 10, 11, 12]、主瓣叠加捕获算法[13]、匹配滤波器和FFT结合处理[14]及基于并行码相位搜索的改进算法[15]。上述算法均具有良好的实用性,其中,并行码相位搜索算法在GPS系统中得到了成熟应用,也有部分学者对该算法进行了改进,使其能够更好地适用于BOC调制信号的捕获,但是存在一个比较共性的问题是,这些改进算法大多以BOC(1,1)调制信号为对象进行分析,分析过程中设定的信噪比一般高于-25 dB,当信噪比低于-28 dB时,采用并行码相位搜索算法不能完成BOC(1,1)信号的捕获。为此,本文以并行码相位搜索算法为基础,分析低信噪比条件下该算法针对BOC调制信号捕获的有效性,并针对BOC(pn,n)调制信号(p为整数)提出了一种基于并行码相位搜索算法和互相关处理相结合的信号捕获算法。该算法的适用性更强,且能够有效地提高BOC(pn,n)调制信号捕获能力。
1 BOC调制 1.1 BOC信号及其自相关特性
BOC信号有BOC(fs,fc)和BOC(α,β)两种表示方法。当表示为BOC(fs,fc)时,fs表示副载波频率(单位MHz),对应副载波半周期为Ts,fc表示扩频码速率(Mchip/s),对应扩频码周期为Tc,当表示为BOC(α,β)时,参数α表示副载波频率与参考频率f0=1.023 MHz比率,β表示码速率与f0比率,即BOC(10.23,5.115)和BOC(10,5)均表示副载波频率为10.23 MHz,码速率为5.115 MHz的BOC信号。在BOC信号中通常定义其副载波调制指数为k=2α/β,且有Tc=kTs。
由此,BOC调制信号的表达式可表示为:
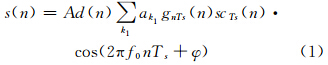
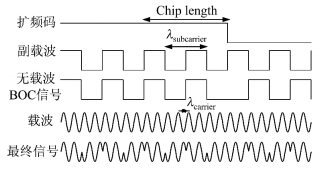
式中,A为信号幅度;d(n)为导航电文; scTs(n)为半周期Ts的方波;gnTs(n)为持续时间为nTs的门函数;ak1为门函数的符号,取值为±1;f0是载波频率;φ为相位偏移。图 1给出一个 BOC调制的实例,扩频码(+1、+1、+1、+1、-1、-1)和方波副载波相乘 (模二乘)后得到无载波的BOC信号,然后用该信号调制载波,得到最终的BOC信号。
|
| 图 1 BOC调制 Fig. 1 BOC Signal Modulation |
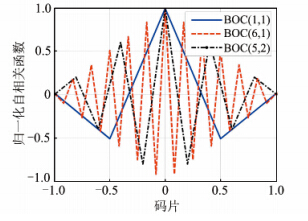
BOC信号的副载波频率是基准频率f0的倍数,但小于信号的载波频率,在信号合成过程中表现为周期为1/fs的方波,而GPS信号仅由扩频码、导航电文和载波3部分组成。即与GPS信号构成相比,BOC信号的构成增加了一个方波形式的副载波信号。因此,BOC信号与GPS信号的自相关函数不同,它包含了伪随机码和副载波两部分的自相关特性,存在多峰值性(图 2),这种多峰值性既会造成BOC信号捕获的不确定性,又使得对不同BOC信号需要有针对性地设计算法才能够有效实现信号的捕获,这也是本文的立足点。
|
| 图 2 BOC信号自相关函数 Fig. 2 Results of Auto Correlation |
综上所述,BOC信号与GPS信号不同,简单利用其自相关函数难以实现信号的捕获,为此,本文将考虑分析BOC信号与其自身伪码的互相关特性,并考虑利用互相关特性进行BOC信号的捕获。对于GPS信号,接收信号剥离载波后与本地PRN码相关即为自相关,产生独立的尖峰。而BOC信号与本地PRN码相关后由于副载波的存在将会受到副载波的影响。
假设本地PRN码为:
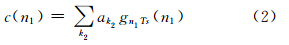
由于本地伪码与导航电文以及载波信号不具有相关性,式(1)、式(2)进行互相关运算时可忽略导航电文和载波两部分,同时忽略幅度因子 A,则有:
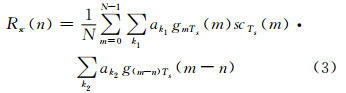
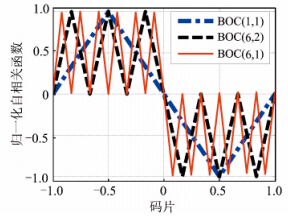
由于Tc=kTs,即在一个伪码周期内有k个半副载波周期,根据滑动相关特性,互相关结果将为伪码本身自相关结果的周期性滑动,且峰值的个数与调制指数k有关。为进一步分析BOC信号与其自身伪码互相关的特性,在不引入噪声条件下,利用Matlab软件分别产生BOC(1,1)、BOC(6,2)和BOC(6,1)等3种信号,并分别与3种信号各自的伪码进行相关,结果如图 3所示。
|
| 图 3 三种BOC信号与伪码互相关结果 Fig. 3 Results of Cross Correlation |
由图 3可见,随着副载波调制指数的增大,互相关结果的峰值越多,且正负峰值的总数正好分别为2、6、12个,对每一种调制均为调制指数的2倍,且由峰值构成的包络连线近似为方波,在1个码片周期中包括有k个峰值,体现了副载波的基本特性。此外,观察BOC(6,2)的互相关结果可见,由于其副载波调制指数与BOC(3,1)一样,其互相关结果也和BOC(3,1)相同,前期许多学者对BOC信号自相关函数的研究也充分证明了这一点。即BOC信号与其伪码的互相关结果和副载波调制指数密切相关,副载波调制指数决定了互相关结果中峰值的个数和分布,由此可将本文的分析结果推广到BOC(pn,n)信号。
2 捕获算法设计与性能分析
FFT并行捕获算法有频域并行搜索和并行码相位搜索两种,在动态非常高的接收机中,两种方式效率接近,均可采用。但一般情况下,采用并行码相位搜索比频域并行搜索效率高。因此,本文以并行码相位搜索算法为基础展开分析。
2.1 并行码相位搜索算法
对任意两个周期为N的序列x(n)和y(n),其相关函数定义为:
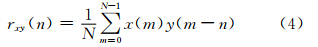
对式(4)进行DFT变换,有:
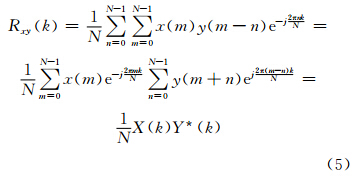
式中,X(k)为x(n)的DFT变换;Y(k)为y(n)的DFT变换;Y*(k)为Y(k)的共轭。式(4)、式(5)结果表明,两个序列时域互相关函数的DFT变换等价于x(n) 的DFT变换的共轭与y(n)的DFT变换的乘积,于是可得并行码相位搜索算法原理如下:接收信号首先与本地载波信号混频去载波,然后进行FFT变换;同时,将本地产生的伪码序列进行FFT变换然后进行共轭运算。两路信号处理完毕后相乘,并进行IFFT变换,然后通过峰值检测判断是否捕获到信号。
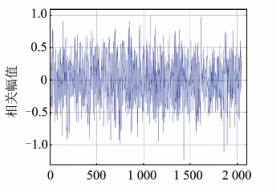
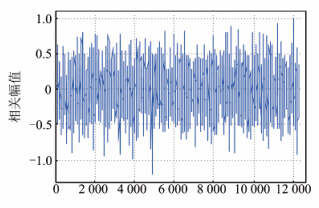
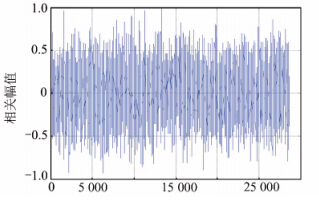
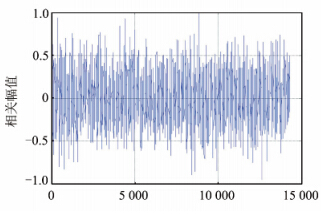
BOC信号的自相关特性不同于GPS信号,BOC信号的捕获是否能够简单地移植并行码相位搜索算法有待进一步分析。因此,本文采用该算法在SNR=-28 dB条件下对BOC(1,1)信号的捕获进行仿真,结果如图 4;在SNR=-20 dB条件下分别对BOC(6,1)、BOC(14,2)和BOC(7,1)信号的捕获进行仿真,结果分别如图 5~图 7所示。
|
| 图 4 BOC(1,1)信号捕获结果 Fig. 4 Acquisition Result of BOC(1,1) |
|
| 图 5 BOC(6,1)信号捕获结果 Fig. 5 Acquisition Result of BOC(6,1) |
|
| 图 6 BOC(14,2)信号捕获结果 Fig. 6 Acquisition Result of BOC(14,2) |
|
| 图 7 BOC(7,1)信号捕获结果 Fig. 7 Acquisition Result of BOC(7,1) |
由图 4~图 7可见,在当前给定信噪比条件下,仅采用并行码相位搜索算法无法完成信号的有效捕获。即要实现低信噪比条件下的BOC信号捕获,可结合BOC信号与其本身伪码互相关函数的特点进行算法改进设计。
2.2 算法改进设计
根据§1.2分析结果可知,对于调制系数为k的BOC信号,与其自身伪码的互相关结果包括2k个峰值,且正负峰各k个。另一方面,利用并行码相位算法进行码相关后的结果应包含有图 3所示的波形,只是由于信噪比较低而无法观察到。因此,本文拟利用上述互相关特性,对上述互相关结果求导并将求导结果作为互相关基准,然后与接收信号的IFFT结果的求导序列进行相关运算,从而完成信号的捕获。以BOC(6,1)为例,其互相关基准序列为{1,-1,1,-1,1,-1,1,-1,1,-1,1,-1,-1,1,-1,1,-1,1,-1,1,-1,1,-1,1}。
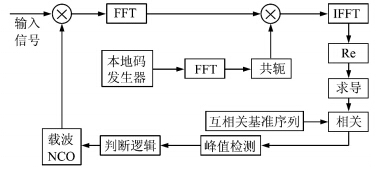
根据上述分析,本文所设计的算法与并行码相位搜索算法的主要区别在于:对经过IFFT变换后的信号首先进行求导处理,然后与BOC信号的互相关基准序列进行相关运算,最后根据相关的结果进行峰值检测及后续处理。为此,在并行码相位搜索算法基础上进行的改进设计捕获算法如图 8所示。
|
| 图 8 改进设计捕获算法 Fig. 8 Improved Acquisition Algorithm |
2.3 改进算法性能分析
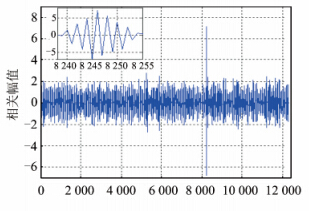
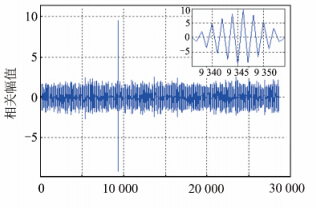
由§2.1可知,对BOC(6,1)、BOC(14,2)和BOC(7,1)信号,当信噪比为-20 dB时,采用经典的并行码相位搜索算法已经无法检测到信号。为了验证所设计改进算法的有效性,本文在SNR=-30 dB,采样率为2fs,延迟码片分别为8 246、3 548、5 964和9 346条件下利用所设计改进捕获算法分别对BOC(6,1)、BOC(7,1)、BOC(10,2)和BOC(14,2)信号进行捕获仿真,结果分别如图 9~图 12所示。
|
| 图 9 BOC(6,1)信号捕获结果 Fig. 9 Acquisition Result of BOC(6,1) |
|
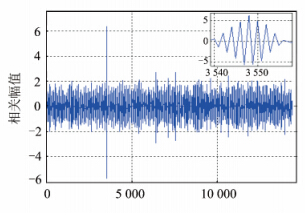
| 图 10 BOC(7,1)信号捕获结果 Fig. 10 Acquisition Result of BOC(7,1) |
|
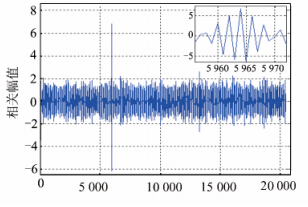
| 图 11 BOC(10,2)信号捕获结果 Fig. 11 Acquisition Result of BOC(10,2) |
|
| 图 12 BOC(14,2)信号捕获结果 Fig. 12 Acquisition Result of BOC(14,2) |
由图 9~图 12可见,在SNR=-30 dB条件下,利用上述改进算法能够有效实现BOC信号的有效捕获,且捕获到的码相位与仿真设置的码相位一致,充分验证了本文所设计改进捕获算法的有效性,且相对采用经典并行码相位搜索算法,改进算法对上述BOC信号改善了信噪比10 dB,提高系统信号搜索灵敏度;此外,根据传统设计,BOC信号的处理应该包括载波环、副载波环和码环3个环路,但如果采用本文设计方法,信号处理将可以减少副载波环这一环节,即可降低接收机开发的硬件成本,对接收机设计具有重要意义。
与此同时,笔者为了研究算法的适用范围,分别利用经典算法和改进算法对BOC(5,2)信号进行了捕获仿真,结果表明,简单移植并行码相位搜索算法完全无法适用。即对BOC(pn,n)信号(p不为整数),简单移植采用并行码相位搜索算法无法完成信号捕获,需要进一步结合信号特征研究新的可行算法。
3 结 语
本文在介绍BOC信号结构基础上,指出BOC信号自相关函数存在多值性,使得BOC信号的捕获不能简单地移植GPS信号的捕获算法;其次,分析了BOC信号的互相关特性,并通过仿真分析对BOC信号的互相关特性进行了总结,同时仿真分析了并行码相位搜索算法对BOC信号进行捕获的有效性;然后,针对经典算法在低信噪比条件下捕获信号存在的不足,结合BOC信号的互相关特性对经典算法进行了改进设计,并以改进算法对BOC(6,1)、BOC(14,2)和BOC(7,1)信号进行了捕获仿真与分析。具体而言,可得出以下基本结论。
1) BOC信号与其伪码的互相关结果体现了副载波方波变化特征;
2) 随着副载波调制指数增大,互相关结果峰值越多,由峰值构成的包络连线越接近于方波特征,且本文分析结果可推广应用于BOC(pn,n)调制信号(p为整数);
3) 经典并行码相位搜索算法在信噪比较低时不能实现BOC信号的正常捕获,且当p不为整数时,经典算法完全不能适用,所以设计BOC信号捕获算法需要结合其信号本身特点进行改进设计;
4) 本文改进设计的捕获算法能够准确地完成BOC(pn,n)信号(p为整数)的捕获,且与经典算法相比,改进捕获算法对本文给定BOC信号能够改善捕获信噪比10 dB以上,可降低接收机设计的硬件成本,能够显著提高接收机捕获灵敏度。
综上所述,本文提出的改进设计捕获算法适用于BOC(pn,n)信号(p为整数)这一类信号,该方法扩展了经典算法的适用范围,提高了接收机的捕获灵敏度,对接收机BOC信号的捕获算法设计具有重要意义。
| [1] | Feng Yongxin, Qian Bo, Liu Fang. Research on PN Code Synchronization Algorithm for TDDM-Based BOC Modulation Signal[J].Journal of Astronautics, 2011, 32(3):645-651(冯永新, 钱博, 刘芳. 基于TDDM 的BOC 调制信号伪码同步算法的研究[J].宇航学报, 2011, 32(3):645-651) |
| [2] | Tang Zuping, Zhou Hongwei, Hu Xiulin, et al. Research on Performance Evaluation of Compass Signal[J].Scientia Sinica, 2010, 40(5):592-602(唐祖平, 周鸿伟, 胡修林, 等. Compass导航信号性能评估研究[J].中国科学, 2010, 40(5):592-602) |
| [3] | Wang Ershen, Zhang Shufang, Zhang Zhixian. Research Status and Trend of Mitigating Multipath Effects Technology for GPS Receiver[J].Telecommunication Engineering, 2011, 51(1):114-119(王尔申, 张淑芳, 张芝贤. GPS 接收机抗多径技术研究现状与趋势[J].电讯技术, 2011, 51(1):114-119) |
| [4] | Chen Xiang, Qi Jiamin, Chen Jiapin. An Novel Unambiguous Synchronization Scheme for BOC(n, n) Signals[J].Science Technology and Engineering, 2012, 12(6):1 268-1 271(陈翔, 齐家敏, 陈佳品. 一种BOC(n, n)信号的新型精确同步方法[J].科学技术与工程, 2012, 12(6):1 268-1 271) |
| [5] | Zaixiu Yang, Zhigang Huang, Shengqun Geng. Acquisition Performance Analysis of BOC Signal Considering the Code Search Step Size[J].Journal of Computers, 2011, 6(7):1 386-1 393 |
| [6] | Zhang Zhongying, Zhang Lixin, Meng Yansong, et al. Study of Acquisition Technology for ALT-BOC Signal[J].Modern Electronics Technique, 2012, 35(5):55-59(张中英, 张立新, 蒙艳松. ALT-BOC信号捕获技术研究[J].现代电子技术, 2012, 35(5):55-59) |
| [7] | Yang Zaixiu, Huang Zhigang, Geng Shengqun. Alternate Binary Offset Carrier Signal Acquisition Algorithm[J].Journal of Nanjing University of Science and Technology, 2012, 36(3):448-452(杨再秀, 黄智刚, 耿生群. 交替二进制偏移载波信号捕获算法[J].南京理工大学学报, 2012, 36(3):448-452) |
| [8] | Yang Zaixiu, Huang Zhigang, Geng Shengqun. Acquisition Performance Analysis of BOC Signal Considering the Code Search Step Size[J].Journal of Computers, 2011, 6(7):1 386-1 393 |
| [9] | Benedetto F, Giunta G, Lohan E S, et al. A Fast Unambiguous Acquisition Algorithm for BOC-Modulated Signals[J].IEEE Transactions on Vehicular Technology, 2013, 62(3):1 350-1 355 |
| [10] | Qi Jiamin, Chen Jiapin, Li Zhenbo, et al. Unambiguous BOC Modulated Signals Synchronization Technique[J].IEEE Communications Letters, 2012, 16(7):986-989 |
| [11] | Yu Changha, Park J I, Lee Y P, et al. Unambiguous BOC Signal Acquisition Based on Recombination of Sub-Correlations[C]. The Eighth Advanced International Conference on Telecommunications, Stuttgart, Germany, 2012 |
| [12] | Yao Zheng, Lu Mingquan, Feng Zhenming. Unambiguous Sine-Phased Binary Offset Carrier Modulated Signal Acquisition Technique[J].IEEE Transactions on Wireless Communications, 2010, 9(2):577-580 |
| [13] | Feng Yongxin, Xu Meirong, Liu Xiantao, et al. Main Lobe Overlapped Acquisition Algorithm of Frequency Domain Based on BOC Modulation Signal[J].Journal of Data Acquisition & Processing, 2012, 27(1):26-31(冯永新, 徐美荣, 刘宪涛, 等. 基于BOC调制信号的频域主瓣叠加捕获算法[J].数据采集与处理, 2012, 27(1):26-31) |
| [14] | He Lu, Lu Zhenpeng, Li Jian, et al. Design and Implement of Acquisition Based on Partial Matched Filters and FFT[J].Science Technology and Engineering, 2012, 12(9):2048-2052(何露, 鲁振鹏, 李健, 等. 基于部分匹配滤波器和FFT 的信号捕获方案的设计与实现[J].科学技术与工程, 2012, 12(9):2 048-2 052) |
| [15] | Chen Xiang. Arithmetic Research and Simulation of BOC Signal Synchronization Based on Xilinx ISE and FPGA[D].Shanghai:Shanghai Jiao Tong University, 2012(陈翔. 基于Xilinx ISE和FPGA的BOC信号同步算法研究和仿真[D].上海:上海交通大学, 2012) |
 2015, Vol. 40
2015, Vol. 40


