文章信息
- 席超, 蔡成林, 李思敏, 李孝辉, 韦照川
- XI Chao, CAI Chenglin, LI Simin, LI Xiaohui, WEI Zhaochuan
- 一种基于三角分区的广域电离层改正新方法
- A New Wide Area Ionospheric Correction Method Based on Triangular Partition
- 武汉大学学报·信息科学版, 2015, 40(3): 390-394
- Geomatics and Information Science of Wuhan University, 2015, 40(3): 390-394
- http://dx.doi.org/10.13203/j.whugis20130068
-
文章历史
- 收稿日期:2013-04-22
2. 中国科学院国家授时中心精密导航定位与定时技术重点实验室, 陕西 西安, 710600
2. Key Laboratory of Precision Navigation Position and Timing Technology, National Time Service Center, Chinese Academy of Sciences, Xi'an 710600, China
电离层延迟误差是影响卫星导航定位精度最大的误差源,也是改善我国北斗卫星导航系统定位精度迫切需要解决的重要问题之一。围绕这一课题,国内外众多学者进行了卓有成效的工作[1,2]。双频接收机用户可以采用双频组合的方式来削弱其影响;对于单频接收机用户而言,电离层延迟误差修正通常有两种方法:① 基于导航电文的电离层参数模型法,如GPS导航电文中的Klobuchar模型,可以消除60%左右的电离层延迟误差;② 采用WAAS格网模型,可以消除80%左右的电离层延迟误差[3,4,5]。
但是以上方法都存在各自的不足之处,如Klobuchar模型的精度不高,难以满足高精度的导航定位应用需求。而WASS格网电离层改正模型对版图比较规整且处于中纬度地区的美国是比较合适的[5],但中国版图呈雄鸡状不规整分布,且低纬度区域在版图中占据的比例较大,采用WAAS格网电离层改正模型,难以从整体上实现我国区域电离层精确改正[6]。针对这一实际问题,本文提出了一种对版图规整性要求低、布站约束较小且满足广域电离层精确改正的方法,称为三角分区的电离层改正法,该方法采用基于中心站辐射的稀疏三角形分区模式。并分别利用我国地震电离层监测网的观测数据及原始GNSS数据进行模型可行性验证,分析结果表明,在保证模型精度的同时该方法较格网模型更为简单有效。 1 电离层延迟改正三角分区法的建立 1.1 区域电离层改正数的生成
区域电离层改正数的生成即基准站天顶方向上电离层延迟量的解算。将区域根据电离层监测站的分布划分为若干三角分区。广域差分系统中基准站天顶方向上电离层延迟改正数是通过选取仰角大于某一值(如40°)时不同方位角的卫星伪距观测值,并进行不敏卡尔曼滤波,再经双频解算提取其穿刺点处的电离层延迟量,然后再通过内插得到。 1.2 用户电离层误差的解算
1) 穿刺点位置及倾斜因子的计算。
2) 反距离幂指数权重插值(IDW)。
基准站到电离层穿刺点的距离为:

式中,wi为电离层基准站i对该穿刺点的权重。
电离层穿刺点处的VTEC的反距离权重插值计算公式为:
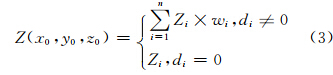
式中,n的值为3;点(xi,yi,zi)为基准站i的大地直角坐标;点(x0,y0,z0)为某一电离层穿刺点下点大地坐标,Zi为基准站i测量得到的其天顶方向的VTEC值;Z(x0,y0,z0)为 基于3个电离层基准站计算得到的该穿刺处的VTEC值。
3) 站-星斜向电离层延迟误差的解算。 1.3 三角分区电离层改正算法
广域电离层延迟误差改正三角分区法就是根据电离层监测站的分布,选择一个地理位置居中的监测站作为中心站,与向外辐射的两个边缘站构成三角几何图形,作为一个三角分区。并将电离层监测站覆盖区域划分为若干三角分区,用户根据电离层穿刺点所落在的三角分区域解算得到的三个顶点(基准站)处的天顶方向电离层延迟数据,通过距离幂指数权重法,求出穿刺点处的电离层数据VTEC。再通过倾斜因子转化为站-星斜向电离层含量TEC。 2 模型精度分析
为了给出较为翔实的结论,本文分别利用中国地震电离层监测网的观测数据和GNSS数据进行两组实验来验证本文方法的可行性。
2.1 算例分析1
利用中国地震电离层监测实验网的监测站及监测数据,选择一部分监测站作为三角分区的基准站构建三角分区,另一部分监测站视为用户电离层穿刺点位置,来验证该方法的可行性。一个三角形分区的服务范围可能是一个网格服务范围的若干倍,为了保证在如此大的范围内该方法的可行性,根据电离层监测网中监测站的分布,对三角分区内部不同位置的若干站点进行验证:居中,靠近三角分区某一边线,或者靠近某一基准站。选择电离层监测网的长春(CHUN)、上海(SHAO)、西安(XIAA)、拉萨(LHAS)、塔什库尔干(TASH)、乌什(WUSH)、德令哈(DLHA)、盐池(YANC)、西宁(XNIN)、蓟县(JIXN)、泰安(TAIN)、郑州(ZHNZ)、海拉尔(HLAR)等13个监测站2012-09-05~11等6 d的垂向电离层延迟数据,为了验证不同时刻该方法的精确度,采用抽样验证,数据采样间隔为1 h,即对一天24个时刻进行模型可行性监测,其中前5个站视为构建中纬度地区广域电离层模型的基准站,后8个站看成检验模型改正效果的验证站,如图 1所示。按照本文提出的三角分区法进行反距离幂指数权重插值,也即IDW-三角分区法,对三角分区法网内和网外的电离层延迟误差改正精度进行拟合验证。
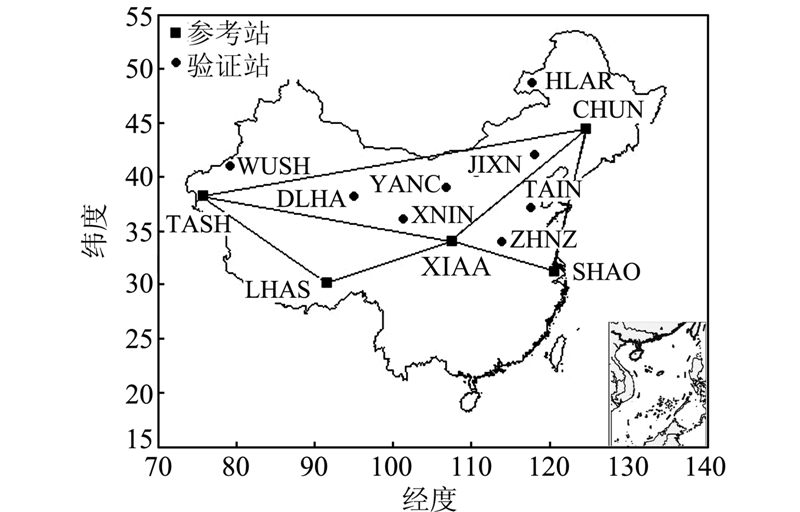 |
| 图 1 我国中纬度地区电离层改正三角分区法组网架构Fig. 1 Network of Ionosphere Correction Triangular Partition Method in Middle-latitude of China |
根据现有电离层测站的分布,把中纬度地区的5个基准站以西安站为中心划分为3个三角形分区域(图 1),即1长春、西安和上海;2长春、西安和塔什库尔干;3拉萨、西安和塔什库尔干;分别对相应区域内的监测站及区域外部周边的监测站进行(拟合)验证,比较拟合值与实测值之间的残差,并从不同方面对模型的精度进行统计分析。由于篇幅的限制,这里仅给出三角分区法网内验证效果图,网内数据拟合精度如图 2所示。
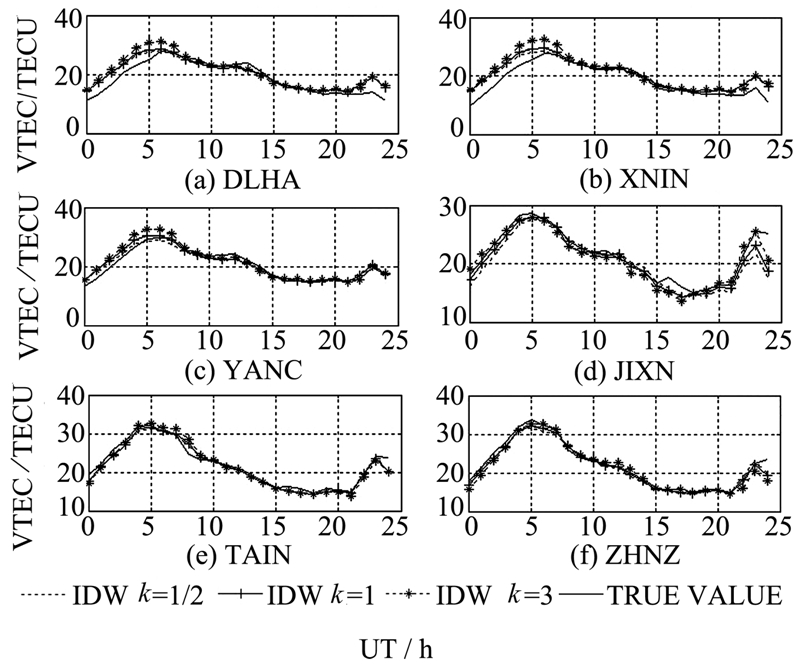 |
| 图 2 不同权重系数条件下三角分区法的网内拟合精度(2012-09-08 UT 0:00-24:00)Fig. 2 Fitting Precision Under Different Weight Coefficient of the Triangular Partition Method (September 8,2012,UT 0:00-24:00) |
表 1~表 2分别从标准差和修正度两个层面分别对网内和网外模型精度进行评估分析。从总体来看,距离的幂指数为1时效果最好,但对于局部一些地区k=1并不是最好,这对于局部区域电离层建模进行优化时是需要考虑的问题。当权重的距离幂指数系数k=1时,该方法有很好的修正精度。三角形区域网内可消除90 %左右的电离层延迟(DLHA 90 %,YANC 94 %,XNIN 88 %,JIXN 94 %,TAIN 92 %和ZHNZ 95 %),反映了模型的精度特征;对于三角形网外几百公里范围内可以使电离层延迟误差改正80%以上(WUSH 90%,HLAR 85%,DLHA 86%和XNIN 87%),且仅使用了5个监测站就实现了对我国几乎整个中纬度地区的服务覆盖,实现了稀疏组网。三角分区法的单分区可覆盖范围广是其可取之处。对于低纬度电离层活动较剧烈的地区,可以适当增加电离层监测站的数量即通过缩小单分区覆盖范围减小内插间隔来降低由磁暴等引起的区域电离层异常影响。
| CHUN/XIAA/TASH | CHUN/XIAA/SHAO | |||||||||||
| DLHA | YANC | XNIN | JIXN | TAIN | ZHNZ | |||||||
| σ | 修正度/% | σ | 修正度/% | σ | 修正度/% | σ | 修正度/% | σ | 修正度/% | σ | 修正度/% | |
| k=1/2 | 2.146 | 89.1 | 1.302 | 92.5 | 1.827 | 88.5 | 2.274 | 91.4 | 1.529 | 92.4 | 1.289 | 94.5 |
| k=1 | 2.064 | 89.5 | 1.112 | 93.6 | 1.938 | 87.9 | 2.120 | 93.5 | 1.662 | 91.8 | 1.167 | 94.8 |
| k=2 | 2.043 | 89.2 | 1.352 | 93.1 | 2.316 | 85.8 | 1.824 | 94.6 | 1.948 | 90.6 | 1.263 | 93.8 |
| k=3 | 2.154 | 88.6 | 1.514 | 92.7 | 2.56 | 84.7 | 1.566 | 94.5 | 2.218 | 89.5 | 1.425 | 92.9 |
| CHUN/XIAA/TASH | CHUN/XIAA/SHAO | |||||||
| WUSH | HLAR | DLHA | XNIN | |||||
| σ | 修正度/% | σ | 修正度/% | σ | 修正度/% | σ | 修正度/% | |
| k=1/2 | 1.982 | 85.5 | 3.079 1 | 81.6 | 3.127 | 86.9 | 2.434 | 87.1 |
| k=1 | 1.275 | 90.0 | 2.668 8 | 84.6 | 3.242 | 86.3 | 2.346 | 87 |
| k=2 | 1.46 | 91.0 | 2.058 6 | 87.2 | 3.468 | 85.1 | 2.309 | 86.4 |
| k=3 | 1.613 | 90.3 | 1.753 1 | 88.1 | 3.468 | 84.1 | 2.374 | 85.6 |
| 注:表 1和表 2中标准差σ的单位是TECU。 | ||||||||
利用GNSS数据进行模型验证,考虑到IGS跟踪站的观测数据完整性以及分布情况,为了便于对三角分区法进行分析,利用地处美国与加拿大的4个跟踪站WILL、SASK、QUIN和BREW进行数据处理,观测站的分布情况如图 3所示,选用2013-07-19的GPS观测数据,数据采样间隔为30 s,选择P1和P2码进行双频电离层解算,并扣除硬件通道延迟。首先利用不敏卡尔曼滤波对伪距观测值进行滤波处理,去除伪码噪声,选择截至高度角为40°的卫星观测值进行电离层的解算,考虑到电离层的变化特征,将15 min整数倍时刻的前后共10 min的电离层数据求平均并归算到15 min整数倍时刻。
 |
| 图 3 利用IGS跟踪站的三角分区组网布局Fig. 3 Network Layout of Triangular Partition Using IGS Tracking Station |
利用GNSS数据分别对跟踪站SASK、QUIN、WILL和BREW进行天顶方向上电离层的解算,各站天顶方向上1 d的电离层变化情况如图 4所示,数据间隔为15min,共95个历元时刻,并给出了利用SASK、QUIN、WILL等3个站的电离层GNSS解算数据,采用三角分区法内插得到的BREW天顶电离层数据与其利用GNSS解算得到的天顶数据的比较。
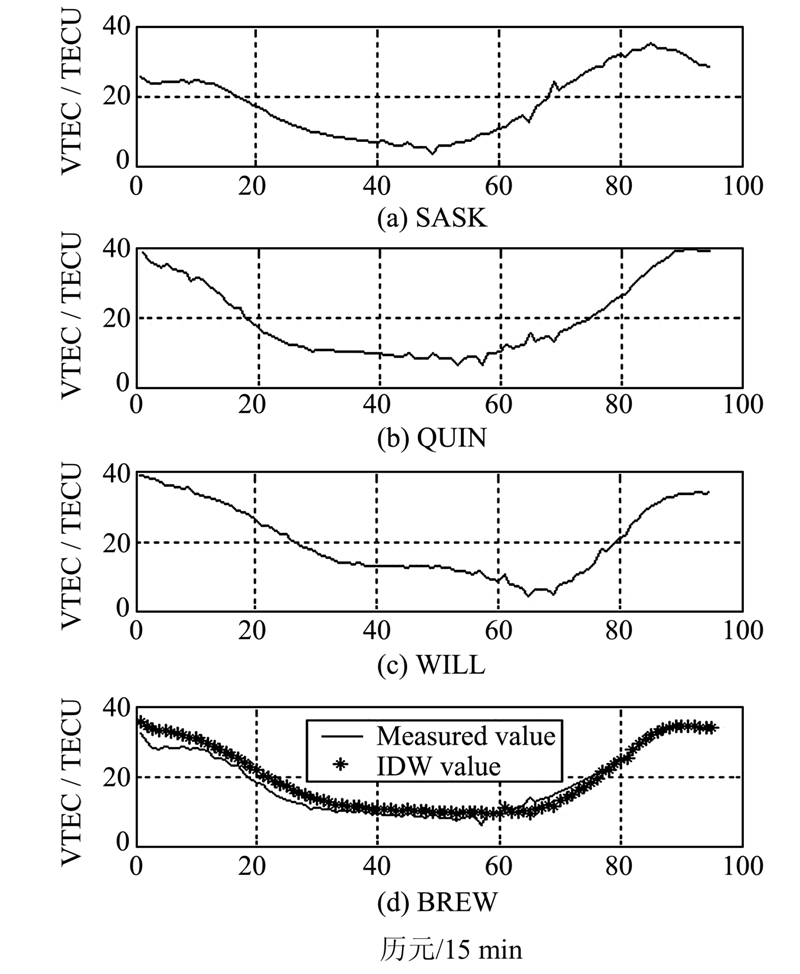 |
| 图 4 2013-07-19利用GNSS数据解算得到的跟踪站天顶方向上电离层变化情况Fig. 4 VTEC of Tracking Stations Based on GNSS Data in July 19,2013 |
验证方案1 把SASK、QUIN和WILL 等3个站看作构建三角分区的基准站,BREW站视为用户电离层穿刺点下点,分别统计95个历元时刻BREW天顶方向上GNSS电离层延迟解算值与三角分区解算值,并进行比较。
验证方案2 把SASK、QUIN和WILL等3个站看作构建三角分区的基准站,BREW站视为用户接收机,在每个历元时刻取落入三角分区内的其中一个穿刺点为验证点,分别统计95个历元时刻的95个穿刺点双频解算电离层值与相应点三角分区解算值,并进行比较。
表 3给出了上述两种方案进行验证的模型精度,利用GNSS数据对三角分区法进行了补充实验验证,通过以上分析结果可以看出,在广域电离层误差改正方面,该方法有着较高的修正精度,误差改正量可以控制在80%以上。
| 验证点 | RMS/TECU | 修正度/% | |
| 验证1 | BREW | 2.410 8 | 86.35 |
| 验证2 | 实际IPPs | 2.616 7 | 84.07 |
对于本文所提出的三角分区法,通过以上两个算例分析,均得到了较好的模型误差修正效果。从而验证了该方法的可行性和有效性。 3 结 语
本文所提出的方法是根据电离层特性参数的空间相关性及我国的地理分布特点,采用电离层改正三角分区的法对电离层监测站覆盖区域进行划分,实现了对中纬度地区电离层的精确改正,它利用监测站的电离层实测数据来现报电离层垂向延迟数据,不依赖于其他的地球物理参量(太阳活动性、地磁活动性等),具有可操作性,易于实现。
三角分区的电离层延迟误差修正结果表明,对于三角形网内区域,该方法可以修正到90 %左右;对于三角形网外几百公里的覆盖区域该方法也能达到80 %以上的修正精度。本文针对差分电离层修正提出了三角分区法这一新的修正方法,有效地解决了不规则区域差分电离层模型建立问题,与格网模型相比,在保证修正精度的同时,它无需划分为大量的网格单元从而降低了计算的复杂性及导航电文的负荷,对广域电离层延迟误差的修正具有重要的参考价值,对于我国广域差分系统建设具有一定参考意义和应用前景。
| [1] | Liu Jingnan, Chen Junyong, Zhang Yanping, et al.Theory and Method of Wild Area Differential GPS[M].Beijing:Surveying and Mapping Press, 1999:90-111(刘经南, 陈俊勇, 张燕平, 等.广域差分GPS原理和方法[M].北京:测绘出版社, 1999:90-111) |
| [2] | Zhang Hongping. Monitoring and Research on Ionosphere Using Chinese Ground Based GPS Network[D].Beijing:Chinese Academy of Sciences, 2006(章红平. 基于地基GPS的中国区域电离层监测与延迟改正研究[D].北京:中国科学院, 2006) |
| [3] | Kumar R, Munjal P. Ionospheric Modeling for WAAS[C]. Proc Annu Meet Inst Navig, Alexandria, VA, 1997 |
| [4] | Yang Zhe, Song Shuli, Xue Junchen, et al .Accuracy Assessment of Klobuchar Model and NeQuick Model in China[J].Geomatics and Information Science of Wuhan University, 2012, 37(6):704-708(杨哲, 宋淑丽, 薛军琛, 等. Klobuchar模型和NeQuick模型在中国地区的精度评估[J].武汉大学学报·信息科学版, 2012, 37(6):704-708) |
| [5] | Fan Guoqing, Wang Wei, Xi Xiaoning, et al. Modeling of Ionosphere VTEC Using Generalized Regression Neural Network[J].Acta Geodaetica et Cartographica Sinica, 2010, 39(1):16-21(范国清, 王威, 郗晓宁, 等.基于广义回归神经网络的电离层VTEC建模[J].测绘学报, 2010, 39(1):16-21) |
| [6] | Li Qiang, Ning Baiqi, Zhao Biqiang, et al. Applications of the CMONOC Based GNSS Data in Monitoring and Investigation of Ionospheric Space Weather[J].Chinese J Geophys, 2012, 55(7):2 193-2 202(李强, 宁百齐, 赵必强, 等.基于陆态网GPS数据的电离层空间天气监测与研究[J].地球物理学报, 2012, 55(7):2 193-2 202) |
 2015, Vol. 40
2015, Vol. 40



