文章信息
- 陈正生, 吕志平, 崔阳, 王宇谱
- CHEN Zhengsheng, LV Zhiping, CUI Yang, WANG Yupu
- 大规模GNSS数据的分布式处理与实现
- Implementation of Distributed Computing with Large-Scale GNSS Data
- 武汉大学学报·信息科学版, 2015, 40(3): 384-389
- Geomatics and Information Science of Wuhan University, 2015, 40(3): 384-389
- http://dx.doi.org/10.13203/j.whugis20130596
-
文章历史
- 收稿日期:2013-10-22
随着全球卫星导航系统(Global Navigation Satellite System ,GNSS)的广泛应用,特别是连续运行基准站(Continuous Operating Reference System ,CORS)的大量建立,使得GNSS观测数据量迅速增长为GNSS数据处理带来了新的挑战。如200个测站组成的网络观测30颗GPS卫星的待估参数最多将达到15 000多个[1],如果再考虑GNSS系统中其他的卫星,则待估参数规模则会更大。面对海量的观测数据,传统的单机集中式的数据处理模式和以单纯增加计算机配置的解决方案已经难以满足需求,寻求大规模GNSS观测数据的快速处理方案是研究热点之一[2,3,4]。近年来,随着网络技术的进步,涌现出了诸如网格计算、云计算的分布式计算新技术,这些新技术的应用以并行计算为基础,为解决海量数据的存储、检索和计算带来了新的发展空间。分布式计算技术以其高效的资源利用效率和计算效率,正逐步应用到大地测量领域。Baboulin[5]、Alleon[6]等对分布式计算技术进行了研究,采用Cholesky或OR分解算法,将平差数学模型分解成矩阵块,利用数值并行计算理论实现重力场模型计算等相关复杂问题的求解。欧空局和日本Kashima空间研究中心VLBI组[7,8,9]在IVS(International VLBI Services for Geodesy and Astrometry)框架下开展了eVLBI网格计算的研究和试验,对VLBI数据进行并行处理。国际大地测量协会 (International Association of Geodesy,IAG)的第1工作组开展Dancer的研究项目,利用分布式计算技术高效快速的处理全球性参考框架数据[10]。国内的研究单位也进行了初步的GNSS测量分布式计算试验[11,12,13],并取得了较好的效果。但是当前的大地测量分布式计算应用还处于试验研究阶段,存在着许多问题需要解决,如分布式计算执行标准、软件的互操作性、计算和平差模型的并行化、计算粒度的划分等。本文将从GNSS数据的分布式处理方法和实现分别进行讨论,并重点对GNSS数据分布式计算的并行化进行研究。 1 GNSS数据分布式处理
分布式计算是将分布的计算单元组织在一起进行协作的一种方式,是建立在分布式系统之上的计算方法。分布式系统是能彼此通信的多个独立计算装置所组成的集合[14]。独立计算装置包 括范围很广,从超大规模集成电路芯片,到紧密耦合共享存储器的多处理器、本地工作站集群、因特网等。分布式计算可以利用整个分布式系统的硬件资源,通过并行解决子计算问题来获得更高的计算性能,以及拥有更大的存储空间。本文对GNSS数据分布式计算过程中的方法、算法设计、处理策略和和对已有软件的利用等方面进行讨论。 1.1 GNSS数据的分布式计算方法
同所有的分布式计算一样,GNSS数据的分布式计算的核心思想为并行计算。首先依据分布式节点的数量、计算任务大小等,对数据进行合理等价的分解,将分解后的数据在各个计算节点上并行运行,然后将计算结果返回主节点进行组合。整个处理流程中,依据解算要求和算法设计流程,反复的执行分解与组合操作,如图 1所示。
 |
| 图 1 分布式计算的处理过程Fig. 1 Processing of Distributed Computing |
分布式计算能快速处理数据的基础是并行计算。并行计算是相对串行计算而言的,指某一时刻同时有若干指令序列(或指令集合)在运行,是利用多种计算资源解决问题的过程[15]。GNSS数据分布式算法的设计即是GNSS数据与算法的并行化过程,包括数据和算法的并行分解,需要考虑的主要因素是并行计算粒度。由Amdahl定律:对给定的一个计算问题,假设串行所占的百分比为α,则使用n个处理机的并行加速比为:

当n增大时加速比S(n)也增大。但是无论使用多少个处理机,加速的倍数不能超过1/α。 在有限的计算任务中,随着节点的增多,节点粒度降低,串行化开销增加,因此,不能盲目地以增加计算节点的数量来提升计算效率。为了方便描述并行计算的性能,加 速比也可以直接设为串行计算时间比上并行处理的总时间。为了发挥分布式计算的最大效能,需要依据数据处理规模、数据分布状态、分布式计算平台或分布式系统的特性(如计算节点、通信带宽等)进行并行化和粒度设计。如在数据准备阶段处理原始观测数据时,由于数据量大,数据相关性小,可以利用网络中的计算机作为分布式计算节点并行处理数据;而在网平差 时,由于涉及的数据量相对较小,通信时间所占的百分比较大,因此,可以充分利用多核环境进行并行计算。 1.3 GNSS数据分布式处理策略
GNSS数据处理通常分为以下3个阶段:数据准备、数据计算和数据成果存储与服务。数据准备包含数据的压缩、传输、解压、格式化等;数据计算包含数据的预处理与解算两个过程,计算比较复杂,是整个数据处理流程的核心;数据成果服务则是将解算结果进行发布,与边界外的用户或软件进行交互的过程。为了发挥分布式计算的最大效用,需要针对不同阶段的特点设计不同的分布式计算方法。表 1显示GNSS数据处理不同阶段的分布式计算方法和策略。
| 阶段 | 分布式方法和策略 |
| 数据准备 | 数据的分布 |
| 数据计算 | 计算和平差模型的分布 |
| 数据服务 | 存储和服务的分布 |
在数据准备阶段,由于不同观测站之间所执行的数据操作相关性小,因此,可以在各个分布式计算节点上并行执行;在数据计算阶段,则需要根据采用的GNSS计算方法和模型以及平差模型来决定所采用的分布式计算方法,其中所涉及的模型和方法比较灵活,难度相对较大;数据成果服务阶段主要是成果数据的存储和服务的分布,需根据用户需求,设计相应的存储和服务方法,以平衡网络负载,发挥分布式系统的作用。数据准备和数据计算两个阶段属于常规数据处理过程,可以参照通用的分布式数据处理方法,而数据计算阶段,GNSS数据计算专业性较强、难度较大,需要重点研究。 1.4 对已有软件的分布式处理
GNSS数据解算专业性强,技术难度高,软件开发周期长,并且每个成熟专业软件都有其特点和用户范围,并不能在短期时间内相互取代。因此,在GNSS数据的分布式计算中,利用已有的软件是计算的一大捷径,不仅可以增加计算的可信度,而且可以减少软件开发的工作量,也不会造成即有资源的浪费。分布式计算要求参与分布计算的子过程,必须能够实现自动化的调用,可以通过功能调用、数据交换、二次开发等方法实现。目前,大部分GNSS数据处理软件(如Bernese、GPSTK等)可以实现数据或功能模块的调用。 2 GNSS数据分布式处理的实现 2.1 GNSS基线分布式解算
基线解算是GNSS数据解算中占用处理时间最长、工作量最大的过程之一,是进行GNSS网平差的基础,其解算质量的好坏直接影响GNSS的定位精度和工作效率。对GNSS载波观测量做双差是最常用的GNSS基线解算方法。随着测站数量的增加,载波双差解算的时间复杂度呈几何级数增长(n3),普通计算机往往难以在短时间内完成大数据量的基线解算,而在分布式系统下可以通过基线解算的并行化设计,实现基线的快速计算:首先将大型计算分解成若干子计算,然后将这些子计算自动分配到网络上的多台计算机(计算节点)上同时解算,最后综合各子计算的结果获取所需的解。
如图 2所示,首先主控制机读取观测网络的元数据和分布式网络信息,由观测网络元数据生成基线,并根据分布式计算网络的信息,如节点数量、服务器数据位置、网络带宽等,决定分解基线的数量和策略,然后将分解后的基线与计算节点进行绑定,并将这些数据以命令的形式通知相关计算节点。各个计算节点在接收到任务命令后,解析命令,并执行相应的基线解算任务,解算完毕后将解算结果发回主机,最后由主控制机异步接收并组合计算各子节点结果,得到最终的计算结果。整个过程对基线解算的任务进行了拆分,使得计算密集型的基线解算得到分解,解算速度和资源利用率得到提高。
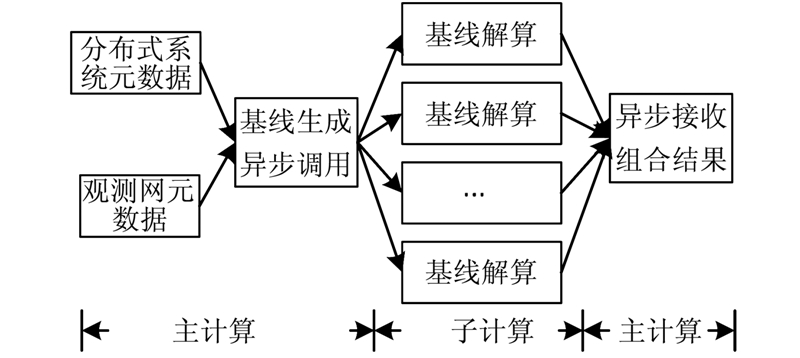 |
| 图 2 GNSS基线分布式计算流程Fig. 2 GNSS Baseline Processing in Distributed Computing |
网平差是GNSS数据处理非常重要的一个过程,是高精度GNSS数据处理的最后一个环节。相同观测点在多次观测和计算中结果的差异,需要通过平差来消除矛盾,得到平差结果。对于大规模网平差,由于计算机配置或操作系统的原因使得单台计算机可用的内存容量有限,当平差规模达到一定程度时,如32位操作系统平差规模达到上万阶,常规的数据平差方法就无法进行计算了。如果在分布式计算环境中,对该任务进行合理、等价的分解与组合,则可以快速地完成解算任务。对于大型网平差,按照观测点进行分区,分区的数量可以依据分布式节点的数 量及解算粒度共同决定。设有r个分区,则分区组成误差方程式为:
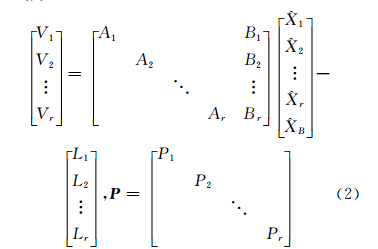
式中,P为权阵,其中第i个子区的误差方程为:

式中,Vi、Li、 i、
i、 B都是向量;Ai、Bi都是矩阵。
B都是向量;Ai、Bi都是矩阵。 i只在第i分区出现,称为区内参数;
i只在第i分区出现,称为区内参数; B出现在各分区,称为联系参数或公共参数。由最小二乘平差原则可得法方程:
B出现在各分区,称为联系参数或公共参数。由最小二乘平差原则可得法方程:
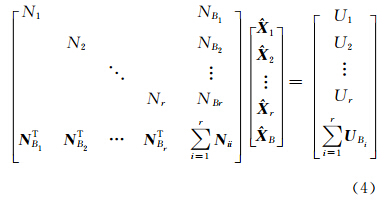
式中,Ni= AiT Pi Ai Ui= ATi PiL ,Ni Bi= AiT Pi Bi,Ui Bi=BiT PiLi,Nii= BiT PiBi,Pi为各分区的权矩阵。则公共参数 B的解为:
B的解为:

式中,
 。公共参数权逆阵Q
。公共参数权逆阵Q B= N -1。将
B= N -1。将 B代入式(4)可得区内参数
B代入式(4)可得区内参数 i的解为:
i的解为:

由式(6),在平差计算过程中,各个子分区之间除了公共参数相同外,其他部分可以分别独立并行计算,其并行过程如图 3所示。
 |
| 图 3 网平差并行计算过程Fig. 3 Parallel Processing of Network Adjustment |
由图 3可以看出,整个平差过程分有3个集中处理和两个并行处理过程。首先是对观测方程进行分解,在各个并行子过程中,由Ai、Bi、Li、 Pi计算出Ni、Ui、 NBi、 UBi、 Nii之后,传回主程序,计算总的 N和U ,进而计算出公共参数XB及其协因数阵QXB,然后在并行子过程中计算各分区内的参数值Xi和协因数阵QXi,最后进行单位权中误差的计算。 3 应用分析 3.1 基线的分布式计算试验
试验程序开发环境为Visual Studio 2012,编程语言为C#,采用.NET 4 Parallel Extensions 作为并行计算开发工具包,运行环境为.NET Framework 4.5,操作系统为64位Windows 7,底层通信技术采用WCF(Windows Communication Foundation)。分布式系统的硬件环境为局域网内的8台硬件配置相当(CPU 2.0 GHz,内存4 GB)的计算机作为计算节点。计算节点通过调用Bernese BPE实现GNSS独立基线解算[16]。GNSS观测数据采用Zip压缩存储在局域网的ftp服务器上。我们选取了2002年第143天北美洲部分区域的637个GNSS观测站进行载波双差计算试验,数据采样率为30 s,观测文件(O文件)达1.56 GB,按照最小生成树原则组成基线,共636条独立基线,基线分布如图 4所示。
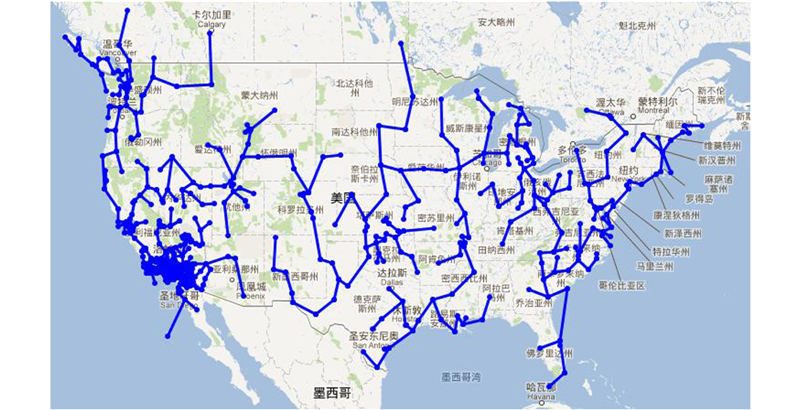 |
| 图 4 GNSS基线分布图Fig. 4 Distribution Diagram of GNSS Baseline |
系统控制端根据任务设置,分配任务到网络中的各个计算节点,自动从指定ftp数据服务器下载原始压缩的观测数据(Z文件),并解压、转换为标准GNSS观测文件,然后执行数据预处理和基线解算。分别采用集中式串行计算和分布式并行计算方法进行基线解算试验,统计计算耗时结果,得到表 2。时间开销以加速比度量,即并行计算与串行计算任务执行时间之比。
| 计算方法 | 时间/min | 加速比 |
| 集中串行 | 652.12 | 1.00 |
| 2个节点 | 348.79 | 1.87 |
| 4个节点 | 185.58 | 3.51 |
| 8个节点 | 102.03 | 6.39 |
由表 2可知,随着参与计算节点的增多,基线解算速度大大加快,2个节点的加速比达到了1.87,4个节点的加速比达到了3.51,而8个节点处理637个测站比单台集中处理的计算速度提高了6.39倍。 3.2 网平差的并行计算试验
为比较集中式与分布并行条件下的大规模网平差的运行效率,考虑到便于控制网平差规模,本试验采用模拟多组GNSS网观测数据的方法进行比较计算,观测数据由计算机随机生成,依据计算节点数量,分成1、2、4、8组数据进行分组平差。由于分布式网平差计算过程中,控制端与子节点要进行频繁的交互,在数据规模不是特别巨大(10万阶以上)的时候,采用多核共享内存的并行处理方法,比采用通过网络传输数据的并行计算方法,能获得更大的并行计算粒度,因此这里采用多核并行的方法进行比较。采用的计算机CPU型号为Intel(R) Core(TM) i7-920、4核心8线程处理器,主频2.67 GHz,内存8 G。观测数量从1 000到10 000,分成8个分区,各分区观测数量相当,分别进行串行、双核并行、4核并行和8核并行试验,统计平均计算时间,得到表 3。
| 观测数量 | 串行 | 并行计算 | 并行加速比 | ||||
| 双核 | 4核 | 8核 | 双核 | 4核 | 8核 | ||
| 1 000 | 1.822 | 0.955 | 0.571 | 0.429 | 1.91 | 3.19 | 4.25 |
| 2 000 | 14.391 | 7.505 | 4.303 | 3.307 | 1.92 | 3.34 | 4.35 |
| 3 000 | 48.317 | 24.984 | 14.554 | 11.293 | 1.93 | 3.32 | 4.28 |
| 4 000 | 114.419 | 58.615 | 33.543 | 26.492 | 1.95 | 3.41 | 4.32 |
| 5 000 | 222.820 | 114.989 | 67.515 | 50.980 | 1.94 | 3.30 | 4.37 |
| 6 000 | 381.866 | 196.934 | 114.256 | 85.728 | 1.94 | 3.34 | 4.45 |
| 7 000 | 605.912 | 319.223 | 185.047 | 136.208 | 1.90 | 3.27 | 4.45 |
| 8 000 | 905.314 | 473.738 | 269.174 | 201.458 | 1.91 | 3.36 | 4.49 |
| 9 000 | 1 289.208 | 678.563 | 391.666 | 286.565 | 1.90 | 3.29 | 4.50 |
| 10 000 | 1 819.311 | 922.551 | 516.866 | 395.950 | 1.97 | 3.52 | 4.59 |
从表 3和图 5可以看出,并行处理方法较串行计算在性能上具有较大程度的提升,且随着测量规模的增大和并行度的增加,这种优势更加明显。在本例中,双核并行计算的平均加速比达到1.88;4核并行平均加速比为3.04;8核并行平均加速比为3.68。1万阶的观测方程,串行计算需要30 min;双核并行需要15 min;4核并行计算需要8 min;8核并行计算只需要6 min。由于本实验计算机处理器为4核心8线程,操作系统显示的8核中4核为逻辑核心,若采用8物理核心处理器并行计算,应能获得更高的加速比。
 |
| 图 5 网平差并行计算比较图Fig. 5 Comparison Chart of Network Adjustment in Parallel Computing |
1) 在GNSS数据处理不同阶段应采用相应的分布式处理策略,在GNSS数据分布式计算中应合理利用已有的GNSS数据处理软件;
2)GNSS数据解算(基线、网平差等)的分布式计算模型和实现是解决大规模GNSS网时效性的主要难点,其中主要的思想是进行合理等价的分解与组合;
3)对于网络传输或串行化所占百分比较大计算,如网平差计算,采用多核共享内存的方法,可以增加计算粒度,获得较大的并行加速比。
| [1] | Blewitt G. Fixed Point Theorems of GPS Carrier Phase Ambiguity Resolution and Their Application to Massive Network Processing:Ambizap[J].Journal of Geophysical Research, 2008, 113:B12410 |
| [2] | Boomkamp H. Global GPS Reference Frame Solutions of Unlimited Size[J].Advances in Space Research, 2010, 46:136-143 |
| [3] | Chen Xiandong. Application of Ambizap Algorithm in Large GPS Network and Its Test Results[J].Geomatics and Information Science of Wuhan University, 2011, 36(1):10-13(陈宪冬. Ambizap 方法在大规模GPS网处理中的应用及结果分析[J].武汉大学学报·信息科学版, 2011, 36(1):10-13) |
| [4] | Jiang Weiping, Zhao Qian, Liu Hongfei, et al. Application of the Sub-network Division in Large Scale GNSS Reference Station Network[J].Geomatics and Information Science of Wuhan University, 2011, 36(4):389-391(姜卫平, 赵倩, 刘鸿飞, 等. 子网划分在大规模GNSS基准站网数据处理中的应用[J].武汉大学学报·信息科学版, 2011, 36(4):389-391) |
| [5] | Baboulin M, Giraud L, Gratton S, et al. Parallel Tools for Solving Incremental Dense Least Squares Problems:Application to Space Geodesy[J].Journal of Algorithms & Computational Technology, 2009, 3(1):117-133 |
| [6] | Alleon G, Amram S, Durante N, et al. Massively Parallel Processing Boosts the Solution of Industrial Electromagnetic Problems:High-performance Out-of-core Solution of Complex Dense Systems[C]. SIAM Conference on Parallel Processing for Scientific Computing, Philadelphia, 1997 |
| [7] | Takeuchi H, Kondo T, Koyama Y, et al. A VLBI Correlator with Internet-based Distributed Computing [EB/OL]. http://www.ursi.org/Proceedings/ProcGA05/pdf/J06.10(0886).pdf, 2012-05-04 |
| [8] | Takeuchi H, Kondo T. Development of Distributed Computing System for VLBI Correlator[EB/OL]. http://wwwsoc.nii.ac.jp/jepsjmo/cd-rom/2004cd-rom/pdf/d006/d006-011_e.pdf, 2012-05-04 |
| [9] | Kondo T, Kimura M, Koyama Y, et al. Current Status of Software Correlators Developed at Kashima Space Research Center[R]. International VLBI Service for Geodesy and Astrometry 2004 General Meeting Proceedings Annual Report, 2004 |
| [10] | Boomkamp H. Global GPS Reference Frame Solutions of Unlimited Size[J].Advances in Space Reaearch, 2010, 46(2):136-143 |
| [11] | Cui Yang, Lv Zhiping, Chen Zhengsheng, et al. Research of Parallel Processing for GNSS Data Under Multi-core Environment[J].Acta Geodaetica et Cartographica Sinica, 2013, 42(5):661-667(崔阳, 吕志平, 陈正生, 等.多核环境下的GNSS网平差数据并行处理研究[J].测绘学报, 2013, 42(5):661-667) |
| [12] | Zou Xiancai, Li Jiancheng, Wang Haihong, et al. Application of Parallel Computing with OpenMP in Data Processing for Satellite Gravity[J].Acta Geodaetica et Cartographica Sinica, 2010, 39(6):636-641(邹贤才, 李建成, 汪海洪, 等.OpenMP并行计算在卫星重力数据处理中的应用[J].测绘学报, 2010, 39(6):636-641) |
| [13] | Wang Peng, Lv Zhiping, Li Changgui, et al. Grid Computing of Terrestrial Reference Frame[J].Bulletin of Surveying and Mapping, 2010(8):37-39(王鹏, 吕志平, 李昌贵, 等.地球参考框架的网格计算[J].测绘通报, 2010(8):37-39) |
| [14] | Attiya H, Welch J. Distributed Computing Fundamentals, Simulations, and Advanced Topics, Second Edition[M].New Jersey:Wiley, 2004 |
| [15] | Yang Liu, Liu Tieying. GPU Architecture of Parallel Computing[J].Journal of Jilin University:Information Sci Ed, 2012, 30(6):629-632(杨柳, 刘铁英.GPU架构下的并行计算[J].吉林大学学报(信息科学版), 2012, 30(6):629-632) |
| [16] | Chen Zhengsheng, Lv Zhiping, Cui Yang, et al. Parallel Computing of GNSS Data Based on Bernese Processing Engine[J].Journal of Geodesy and Geodynamics, 2013, 33(5):79-82(陈正生, 吕志平, 崔阳, 等.基于BPE的GNSS数据并行快速解算[J].大地测量与地球动力学, 2013, 33(5):79-82) |
 2015, Vol. 40
2015, Vol. 40


