文章信息
- 甘雨, 隋立芬, 戚国宾, 张鹤
- GAN Yu, SUI Lifen, QI Guobing, ZHANG He
- 陆地导航中GNSS/陀螺仪组合实时测姿方法
- A Real-Time Attitude Determination Approach for Land Navigation Based on GPS/Gyroscope Integration
- 武汉大学学报·信息科学版, 2015, 40(3): 379-383
- Geomatics and Information Science of Wuhan University, 2015, 40(3): 379-383
- http://dx.doi.org/10.13203/j.whugis20130209
-
文章历史
- 收稿日期:2013-06-05
姿态对于陆地导航系统的定位和控制具有重要作用,目前最常用的定姿方式是惯性导航(INS)。陆地导航系统中,采用的惯性测量单元(IMU)通常不超过战术级的标准,需和GNSS组合以控制其误差积累。
目前,GNSS测姿主要包括多天线测姿和单天线测姿[1,2,3,4]。多天线测姿具有结构复杂,安装难度大、体积大和成本高的缺陷,当载波相位整周模糊度不能很好地解算时,得到出来的姿态结果精度非常差[5]。单天线测姿法由Kornfeld等人提出并用于飞行器姿态确定[6,7],这种姿态由速度或位置增量导出,故被称为伪姿态,在满足协调飞行时[8,9],伪姿态接近常规姿态。单天线测量姿态在组合导航系统中常被作为备份姿态信息或者故障检测信息[10]。Lai用三轴陀螺仪和单天线GPS进行组合测姿[11],但组合姿态精度基本受GPS姿态值控制,陀螺贡献不大。
陆地导航实践中,最关心的是航向角的精度和可靠性,俯仰角和横滚角一般数值较小影响较弱。在这种情况下,使用GNSS/INS组合导航会增加系统成本。本文提出仅利用一个陀螺仪和单天线GNSS组合进行实时测姿,先由单天线GNSS计算姿态角3参数,再将陀螺信息与GNSS导出的航向角进行融合。分析了单天线测姿在载体静止或低速运动时精度很差的原因,提出了在组合滤波中进行解决的方案。推导了GNSS和陀螺信息融合的滤波模型,将陀螺仪信息作为状态模型的控制输入,以GNSS航向为观测值。最后利用实测陆地导航数据验证了组合算法的可靠性。 1 单天线GNSS测姿 1.1 单天线GNSS测姿原理
常规姿态表征的是载体系和地理系之间的旋转关系,伪姿态表征的是载体速度系和地理系之间的旋转角,在陆地导航问题中,载体坐标系和载体速度坐标系之间差别微小,后续讨论将伪姿态作为常规姿态。
载体速度坐标系和地理坐标系旋转关系用3个欧拉角来表示。载体速度矢量表示为 v R,则航向ψp为θr在水平面的投影vh与地理北方向的夹角,俯仰θp为θr和水平面夹角,即θr和vh的夹角,横滚rp指以v系X轴在水平状态时的指向为参照,X轴绕Y轴的旋转角[9]。
航向角ψp可由东、北向速度计算得到:
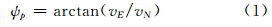
也可以由水平方向速度计算:
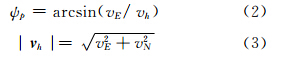
俯仰角为:
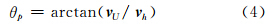
横滚角由飞行器动力学知识给出[6]:
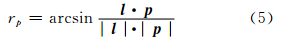
式中,l 为举力加速度:

式中,a为加速度; g为重力。加速度可由GNSS测得的速度进行滤波计算得到。而

单天线测姿的基础为GNSS测速。GNSS多普勒观测方程为:

式中,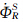 为多普勒;
为多普勒; 为距离变化率;
为距离变化率;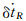 和
和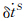 为钟速;
为钟速;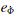 为观测噪声。
为观测噪声。
由式(8)计算出速度并转换到地理坐标系后,由式(1)、式(4)、式(5)可计算出3个姿态角。 1.2 低速运动时单天线GNSS姿态补偿
在单天线GNSS姿态计算的公式中,分母由速度量构成,当载体静止或速度非常小时,数学上造成数值不稳定性,而且速度测量误差可能会淹没真实速度值。
Chiang在GPS/INS组合导航中应用INS力学编排计算的姿态对GPS姿态进行递推,载体由k时开始静止,可用式(9)计算航向:
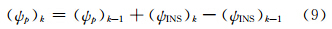
即静止后仅使用INS姿态更新。该法进行姿态更新的同时无法对其对应的随机模型进行更新,当GNSS姿态信息重新可用时缺乏可靠的滤波模型保证组合的进一步运行。
本文将陆地导航的GNSS航向补偿结合到和陀螺仪组合的滤波模型中一并考虑,以确保航向信息的连续可靠性。 2 GNSS/陀螺仪组合滤波模型
为提高陆地导航的航向精度,引入一个陀螺仪和GNSS进行组合,陀螺仪沿载体坐标系Z轴(向上)安装。
陀螺仪所测角速度转换成航向角速度需进行位置速率和地球自转速率补偿。设陀螺测得角速度值为ωz,则航向角变化率为:
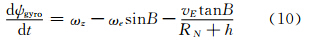
式中,ωe为地球自转角速度;B为纬度; RN为卯酉圈曲率半径;h为大地高。
在这里的组合中,航向角、航向角误差乃至航向角速度都可以作为滤波的状态参数,为了形式上保证简洁性,这里使用航向角为状态参数。设航向角以ψ表示,则有:

其中,(Δψ)k,k-1表示k-1到k时刻的真实航向变化量,可以写为:

式中,(Δψgyro)k,k-1为由陀螺导出的航向变化量;用wk表示陀螺导出航向角变化值中的白噪声成分;br,k-1表示时间相关零偏。
结合式(11)、式(12)可以得到航向角的状态方程:
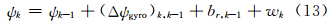
其中,(Δψgyro)k,k-1相当于滤波控制输入:
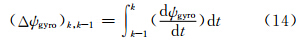
br,k-1为有色噪声成分,这 里用一阶高斯马尔可夫(Gauss-Markov)模型进行建模。连续一阶G-M模型为:

式中,η(t)为标准分布白噪声过程;βc=1/Tc,Tc为相关时间;σ2br为br(t)的方差。
对式(15)进行离散化,可得:
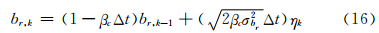
式中,Δt为k-1与k历元的时间间隔。
综合式(13)、式(15),可得状态方程:
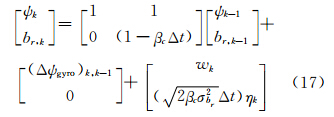
由GNSS航向角数据建立的观测方程为:
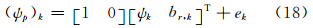
式中,ek为GNSS航向测量误差。
式(17)和式(18)即为Kalman滤波的状态模型及观测模型,当载体处于静止或超低速运动状态时,GNSS航向数据不可靠,仅采用式(17)的状态预测进行航向更新:
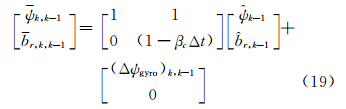
式(19)和式(9)有两处不同:① 式(19)顾及了零偏项br的影响,利用前面估计出的零偏结果削弱误差积累;② 采用式(19)的同时进行随机模型的更新,这样当GNSS航向数据重新可用时,可以保证滤波模型的准确性,加快滤波收敛。
俯仰角和横滚角在陆地导航中并不是必需量,一般仅作为参照数据,不纳入导航参数的推算中,直接使用GNSS结果即可。 3 计算与分析
采用实测陆地导航数据验证,实验基本在水平地面上进行,将使用3轴陀螺的INS与GPS RTK组合得到的航向角作为参考值。利用实验中的两段数据进行探讨,其中,数据1不包含静止或超低速运动状态,数据2包含一段时间的静止或低速状态。
共设计两种计算方案: 方案1采用单天线GPS计算航向角; 方案2采用GPS/陀螺仪组合方法计算航向角。
实验数据1两种方案的误差分别如图 1、图 2所示,误差的RMS和MAX(最大误差)如表 1所示;实验数据2的结果如图 3、图 4所示,RMS和MAX如表 2所示。
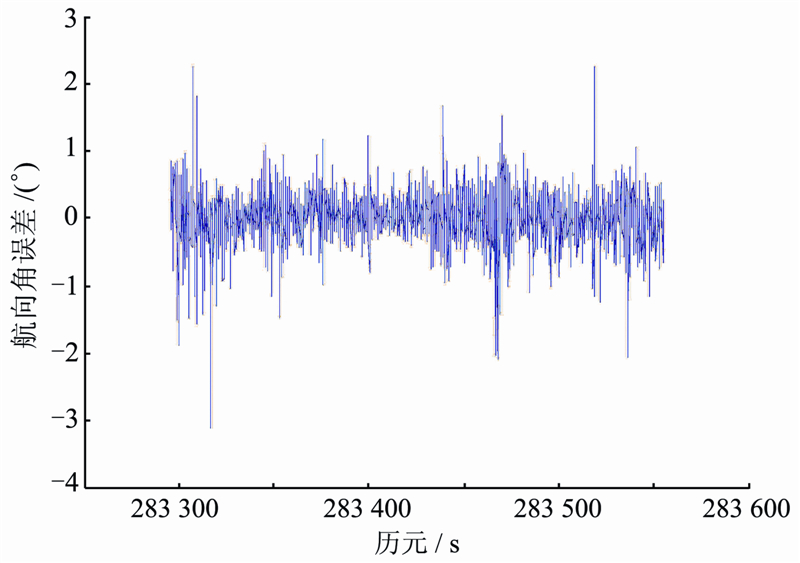 |
| 图 1 数据1 GPS航向角误差Fig. 1 GPS Heading Error of Data 1 |
 |
| 图 2 数据1 GPS/陀螺组合航向角误差Fig. 2 GPS/Gyro Heading Error of Data 1 |
| RMS/(°) | MAX/(°) | |
| GPS | 19.804 | 184.537 |
| GPS/Gyro | 0.061 | 0.134 |
从上述结果中可以看出:
1) 单天线GNSS测量的姿态是基于测速信息计算的,所得姿态噪声水平很高,虽然具有长期较稳定特性但是短期精度较低。
2) GNSS/陀螺仪组合在可靠的滤波模型基础上,利用Kalman滤波能够较好地结合两者的优势,在长期和短期精度上同时达到优化,计算结果噪声小,精度和可靠性相对GNSS均有较大提升。
从图 3、图 4及表 2结果可以得出结论。
 |
| 图 3 数据2 GPS航向角误差Fig. 3 GPS Heading Error of Data 2 |
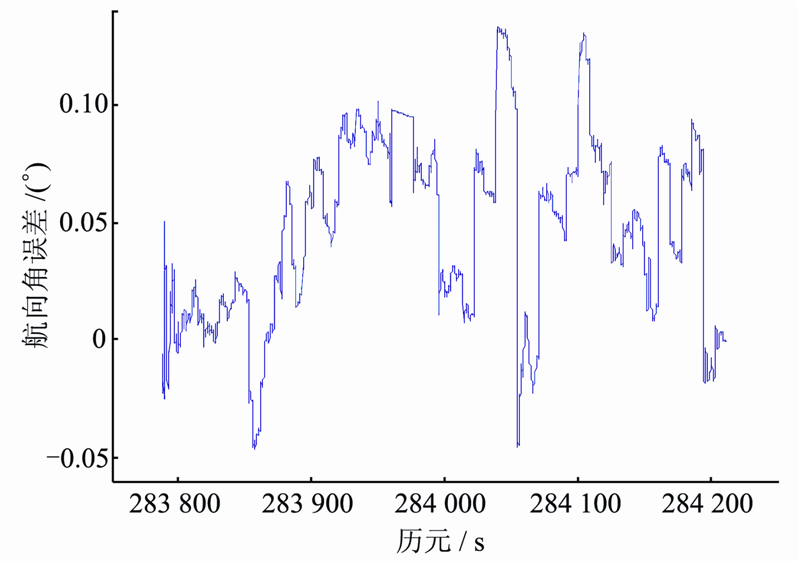 |
| 图 4 数据2 GPS/陀螺组合航向角误差Fig. 4 GPS/Gyro Heading Error of Data 2 |
| RMS/(°) | MAX/(°) | |
| GPS | 0.367 | 3.117 |
| GPS/Gyro | 0.125 | 0.257 |
1) 当载体静止或速度极低时,基于GNSS速度信息的单天线GNSS不能进行姿态确定。
2) GNSS/陀螺仪组合测姿过程中,对于载体静止或低速状态,仅使用滤波的预测更新,能够在一定程度上克服GNSS不可用带来的影响,由于进行了随机模型的同步更新,在重新获得可用GNSS航向时,滤波能够迅速收敛。 4 结 语
航向角精度是影响陆地导航性能的关键因素。使用GNSS/INS组合会增加多余成本,仅使用一个陀螺仪时无法抑制航向误差的发散。单天线测姿系统噪声水平较高,且在静止及低速状态下不可靠。本文提出的单陀螺仪和单天线GNSS组合测姿方法能够避免多天线GNSS测姿的模糊度固定问题,很好地满足实时性需求。GNSS/陀螺仪组合测姿吸收了陀螺仪短期精度高和GNSS单天线测姿长期稳定性高的优点,避免了使用陀螺仪时的发散现象,同时降低GNSS测姿的噪声水平,航向角整体精度可提高数倍。
由于俯仰角和横滚角并不是陆地导航的关键参数,这里直接使用GNSS姿态结果。如果需要克服静止或低速状态下的GNSS俯仰和横滚不可靠问题,可以引入成本较低的加速度计进行辅助。
| [1] | Zhao Jianhu, Liu Jingnan, Zhou fengnian. Method in Determining Vessel Attitude with GPS[J].Journal of Wuhan Technical University of Surveying and Mapping, 2000, 25(4):353-357(赵建虎, 刘经南, 周丰年. GPS测定船体姿态方法研究[J].武汉测绘科技大学学报, 2000, 25(4):353-357) |
| [2] | Liu Genyou, Ou Jikun.Determining Attitude with Single Epoch GPS Algorithm and Its Precision Analysis[J].Geomatics and Information Science of Wuhan University, 2003, 28(6):732-735(刘根友, 欧吉坤. GPS单历元定向和测姿算法及其精度分析[J].武汉大学学报·信息科学版, 2003, 28(6):732-735) |
| [3] | Wang Bing, Sui Lifen, Xiao Guorui, et al. Comparison of Attitude Determination Approaches Usiing Multiple Global Positioning System(GPS) Antennas[J].Geodesy and Geodynamics, 2013, 4(1):16-22 |
| [4] | Gebre-Egziabher D, Hayward R, Powell D. Design of Multisensor Attitude Determination Systems[J].IEEE Trans AerospElectron Syst, 2004, 40(2):627-649 |
| [5] | Wang Lei, Zhai Guojun, Zhao Junsheng, et al.A New Method for Vessel Attitude Determination Using GPS[J].Geomatics and Information Science of Wuhan University, 2006(12):1 071-1 074(王磊, 翟国君, 赵俊生, 等.一种利用GPS进行船只姿态测量的新方法[J].武汉大学学报·信息科学版, 2006(12):1 071-1 074) |
| [6] | Kornfeld R P, Hansman R J, Deyst J J. Single-Antenna GPS-Based Aircraft Attitude Determination[J].Journal of the Institute of Navigation, 1998, 45:51-60 |
| [7] | Kornfeld R P, Hansman R J, Deyst J J, et al. Applications of Global Positioning System Velocity-Based Attitude Information[J].Journal of Guidance, Control, and Dynamics, 2001, 24:998-1 008 |
| [8] | Liu Ruihua, Zhang Peng. Study on Pseudo-attitude Determination Technology Based on Single-Antenna GPS Receiver[J].IEEE Second International Conference on Information and Computing Science, 2009:84-86, doi:10.1109/1C1C.2009.28 |
| [9] | He Jie, Huang Xianlin, Wang Guofeng. Design and Application of Single-antenna GPS/Accelerometers Attitude Determination System[J].Journal of Systems Engineering and Electronics, 2008, 19(2):220-227 |
| [10] | Deyst J, Richard J, Kornfeld P, et al. Single Antenna GPS Information Based Aircraft Attitude Redundancy[C]. Proceedings of the American Control Conference, San Diego, California, 1999 |
| [11] | Lai Y, Jan S. Attitude Estimation Based on Fusion of Gyroscopes and Single Antenna GPS for Small UAVs Under the Influence of Vibration[J].GPS Solutions, 2011, 15(1):67-77 |
| [12] | Chiang K. INS/GPS Integration Using Neural Networks for Land Vehicular Navigation Applications[D].Canada:Department of Geomatics Engineering, University of Calgary, 2004 |
 2015, Vol. 40
2015, Vol. 40


