文章信息
- 向涛, 史俊波, 郭际明
- XIANG Tao, SHI Junbo, GUO Jiming
- GPS广播星历非整点时刻数据块性能分析
- Quality Assessment of Non-integer-hour Data Blocks in GPS Broadcast Ephemeris
- 武汉大学学报·信息科学版, 2015, 40(3): 372-378
- Geomatics and Information Science of Wuhan University, 2015, 40(3): 372-378
- http://dx.doi.org/10.13203/j.whugis20130593
-
文章历史
- 收稿日期:2013-10-21
2. 武汉大学精密工程与工业测量国家测绘地理信息局重点实验室, 湖北 武汉, 430079;
3. 桂林理工大学广西空间信息与测绘重点实验室, 广西 桂林, 541004
2. Key Laboratory of Precise Engineering and Industry Surveying, National Administration of Surveying, Mapping and Geoinformation, Wuhan University, Wuhan 430079, China;
3. Guangxi Key Laboratory of Spatial Information and Geomatics, Guilin University of Technology, Guilin 541004, China
近年来,得益于新型卫星发射、地面控制站设施改善和数量增加以及预报模型算法的改进,GPS广播星历精度有了较大的提高,整体精度已经优于1 m [1, 2, 3]。目前,对GPS广播星历的研究多集中在精度分析上,却回避了这样一个问题:广播星历数据块每两小时更新一次,理论播发时刻是0,2,…,22等GPS整点时刻,但由于GPS卫星与地面控制站固件异常,导航文件中会出现非整点时刻数据块[4],这些非整点时刻数据块发生在整点时刻前的16*N s(N=1,2,…,15)。根据UNAVCO对2011全年广播星历数据测试结果,在149 909个 星历数据块中,非整点时刻数据出现了25 619次,其中,N=1的情况出现了24 306次,远高于其他N的取值,且没有出现N大于15的情况[5]。
非整点时刻和整点时刻星历数据块的区别首先表现在卫星星历或卫星改正数的IODE不一样,具体应用包括使用RTCM 2.3版本的Type1、20、21进行距离观测值改正,以及RTCM 3.1版本的Type1057、1058进行卫星轨道、时钟误差改正。当用户使用的星历IODE和RTCM改正数的IODE不一致时,将会影响到距离观测值或卫星轨道、时钟误差,从而影响最终的定位结果 。
本文首先描述了GPS广播星历中非整点时刻数据块的三种类型,并针对第二类非整点时刻数据块设计了质量分析策略,通过一周的算例分析了非整点时刻数据块的精度,最后给出了使用GPS非整点时刻星历数据块的建议。
1 GPS广播星历非整点时刻数据块
在GPS定位中,广播星历的质量直接影响卫星轨道和钟差精度。GPS卫星和地面控制站固件问题会时常导致星历文件异常,如数据丢失、不连续和冗余,非整点时刻数据块属于广播星历异常的一种[4, 6],GPS导航文件中非整点时刻数据块主要有3种形式,见表 1。
| 类型 | 描述 | 示例 |
| S1 | 无整点时刻星历数据块,有该整点时刻前16×N s非整点时刻数据块 | … 06:00:0007:59:44 10:00:00 12:00:00 … |
| S2 | 有整点时刻星历数据块,同时有该整点时刻前16×N s的非整点时刻数据块 | … 06:00:0007:59:44 08:00:00 12:00:00 … |
| S3 | 无整点时刻星历数据块,有连续两个非整点时刻数据块 | … 06:00:0007:59:28 07:59:44 10:00:00 … |
表 2统计了2013年年积日121~127 GPS广播星历非整点时刻数据块信息,T表示星历数 据块的总数,S1、S2、S3分别表示第1、第2、第3类非整点时刻数据块的数量。由表 2可知,3种类 型非整点时刻数据块约占所有数据块的16%,这一比例与UNAVCO对2011全年广播星历非整点时刻数据块的统计比例17% 一致[5]。出现第一类非整点时刻数据块时,用户没有更优选择,只能使用该数据块;而第3类比例太小,因此,本文研究对象为第2类非整点时刻数据块。
| 年积日 | S1 | S2 | S3 | T | S/T/% | S2/T/% |
| 121 | 34 | 33 | 0 | 420 | 16.0 | 7.9 |
| 122 | 35 | 34 | 0 | 420 | 16.4 | 8.1 |
| 123 | 31 | 33 | 2 | 420 | 15.7 | 7.9 |
| 124 | 36 | 30 | 0 | 418 | 15.8 | 7.7 |
| 125 | 36 | 30 | 0 | 417 | 15.8 | 7.2 |
| 126 | 32 | 30 | 2 | 417 | 15.3 | 7.2 |
| 127 | 37 | 33 | 0 | 407 | 17.2 | 8.1 |
| 合计 | 241 | 223 | 4 | 2 919 | 16.0 | 7.7 |
对所有GPS卫星7 d内的第2类非整点时刻数据块进行统计,结果见图 1,横轴表示卫星号,纵轴表示非整点时刻数据块随年积日的累计量。图 1显示,7 d内PRN09出现第2种非整点时刻数据块多达12次,PRN17等卫星非整点时刻数据块最少出现5次,23颗卫星平均每天至少发生1次第2类非整点时刻星历数据块。

|
| 图 1 第二类非整点时刻数据块数量统计 Fig. 1 Numbers of the Second Type Non-integer-hour Data Blocks in Broadcast Ephemerides |
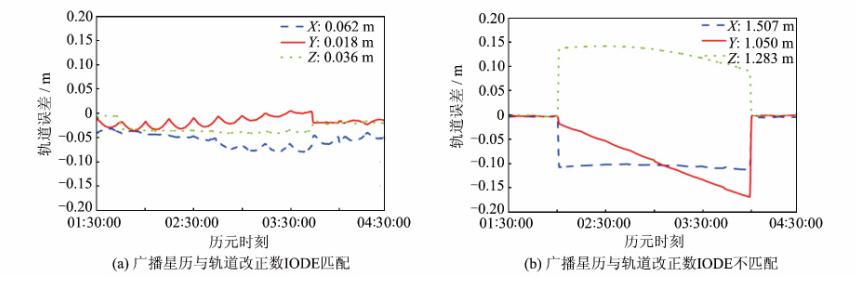
以年积日124 d的PRN08卫星为例,该星在03:39:44有一个非整点时刻星历数据块,同时在04:00:00存在一个整点时刻数据块。IGS实时服务(Real-Time Service,RTS)提供的RTCM 3.1 Type1057(轨道)、1058(时钟)改正数是基于04:00:00计算的。对于这种情况,若不考虑非整点时刻和整点时刻数据块的区别,将会导致卫星轨道改正的错误。如图 2所示,当使用匹配的改正数时,实时轨道精度为0.074 m;而使用不匹配的改正数,实时轨道改正出现了异常,精度为1.967 m,甚至低于不使用改正数的广播星历轨道精度。
|
| 图 2 GPS PRN08卫星实时轨道误差 Fig. 2 Real-time Satellite Orbit Error with Different IODE Matches for PRN08 |
如前所述,广播星历非整点时刻数据块在导航文件中非常普遍,它的存在对用户接收实时改正电文形成了干扰。若非整点时刻星历数据块是系统产生的粗差数据,将会对用户带来不可忽视的影响。因此,探究非整点时刻星历数据块的性能,定性给出其与相应整点时刻星历数据块的质量差异具有重要的意义。
2 数据分析策略
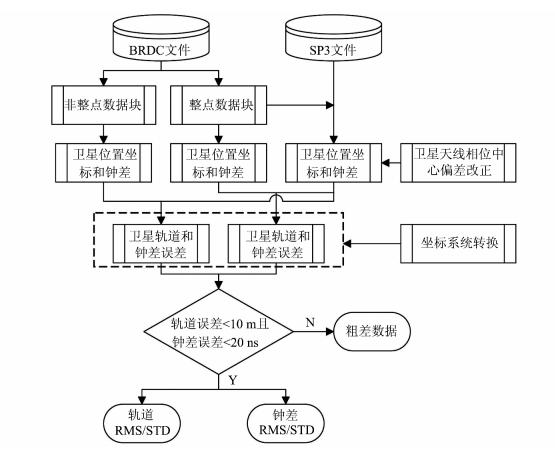
分别使用GPS广播星历非整点时刻与相应整点时刻数据块计算该整点时刻前后各两小时间隔内每隔1 s的卫星轨道坐标和钟差,以IGS精密星历为参考,处理流程见图 3。输入GPS广播星历与精密星历,一旦搜索到第二类非整点时刻数据块,便利用精密星历计算卫星的参考坐标和钟差,从而获得非整点时刻与整点时刻广播星历数据块的轨道和钟差误差,若轨道误差大于10 m或钟差误差大于20 ns,则认为该历元数据为粗差数据并剔除,反之则进行精度分析[7, 8]。
|
| 图 3 非整点时刻数据块性能分析流程 Fig. 3 Flowchart of Quality Assessment of Non-integer-hour Data Blocks |
在数据分析过程中需注意两个问题:
1) 广播星历求得的卫星坐标基于WGS-84坐标系,而IGS精密星历提供的卫星坐标基于ITRF框架,两参考框架存在几个厘米差异,这种差异与广播星历自身误差相比相对较小,在本文中未考虑;
2) 广播星历获取的卫星坐标相对于卫星天线相位中心,而IGS精密星历提供的卫星坐标相对于卫星质心,这项偏差对于卫星瞬时位置可达到2 m,因此必须使用IGS提供的ANTEX文件加以改正[9, 10]。
轨道误差通常由径向 R 、切向 A和法向C等 3个分量进行描述,因此,需将卫星位置误差从地心地固坐标系转换到轨道坐标系。具体做法是将WGS-84坐标系中的广播星历卫星位置误差矢量投影到轨道坐标系的径向、切向和法向[11, 12, 13]。用 r和 分别表示WGS-84坐标系下卫星的绝对位置矢量和速度矢量,卫星位置误差矢量为δ r =[Δx Δy Δz]T,根据直接转换法有:
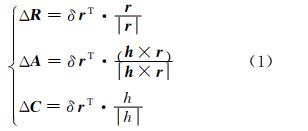
式中,h = r ×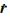 。
。
由于广播星历与精密星历存在时间基准差异,在分析非整点时刻与整点时刻数据块卫星钟差精度时,选择某颗卫星的钟差作为参考,其余卫星与该参考卫星进行卫星间求差,以消除时间基准差异的影响,将单差后的钟差误差Δ CLK作为评估卫星钟差精度的统计量。
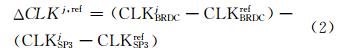
式中,上 标ref指参考卫星;j为计算卫星;下标BRDC和SP3分别表示广播星历和IGS精密星历。
用 R i表示计算历元i卫星轨道误差的径向分量,R为所有历元径向误差均值,n表示历元个数,径向误差的均方根误差 RMS_R和标准偏差误差STD_R为:
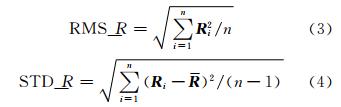
对单天内所有32颗GPS卫星轨道径向误差RMS_ALL_R 计算公式如下:
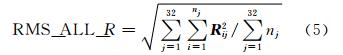
式中,nj表示第j颗卫星计算历元个数,R ij表示第i颗星第j历元的径向轨道误差。切向、法向轨道误差及钟差误差的精度统计与式(3)~式(5)相同。
3 非整点时刻数据块质量分析
选取卫星非整点时刻与相应整点时刻星历数据块,通过轨道和钟差精度分析,首先证明非整点时刻数据块并非粗差。对所有GPS卫星非整点时刻数据块进行连续7 d的分析,证明非整点时刻数据块精度优于整点时刻数据块。
3.1 任一非整点时刻数据块分析
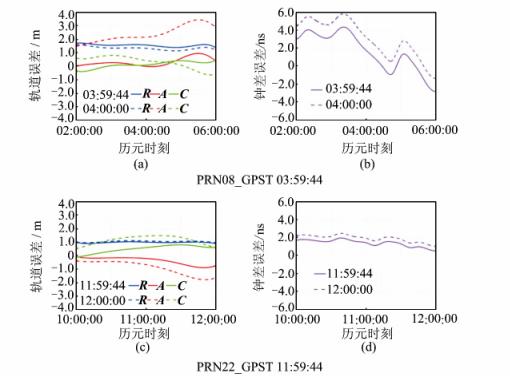
年积日第124天PRN08(Block II F,Cs)和PRN22(Block II R,Rb)卫星的一次非整点时刻数据块分别发生在03:59:44和11:59:44。将卫星轨道误差的径向、切向和法向分量及钟差误差绘制误差时间序列,见图 4。实线和虚线分别表示广播星历非整点时刻和相应整点时刻数据块的计算结果,其中,PRN07为参考卫星。
|
| 图 4 PRN08和PRN22非整点时刻与整点时刻数据块轨道误差 Fig. 4 Orbit and Clock Errors of Non-integer-hour and Integer-hour Data Blocks for PRN08 and PRN22 |
图 4(a)和4(c)显示,PRN08和PRN22非整点时刻与整点时刻数据块轨道误差的径向、切向和法向分量时间序列具有相近的变化趋势,尤其在径向误差上两者近乎重合。图 4(b)和4(d)显示,两种时刻数据块的钟差误差同样表现出非常一致的变化趋势;而PRN08钟差误差的大小和波动明显大于PRN22,验证了铯钟短期稳定性和准确度不如铷钟的物理特性[10]。综合轨道和钟差两方面结果,认为广播星历非整点时刻数据块并非粗差数据。
表 3对PRN08和PRN22卫星轨道误差与钟差误差的RMS和STD进行了统计。结果表明,非整点时刻数据块的轨道精度和钟差精度均优于整点时刻数据块。两种数据块轨道误差的差异主要体现在切向和法向,而径向误差较为一致。钟差方面,非整点时刻与整点时刻数据块钟差误差STD值相同,而RMS值不同,反映了两者具有系统性偏差。
| PRN | GPST | RMS | STD | ||||||||
| 径向/m | 切向/m | 法向/m | 三维坐标/m | 时钟/ns | 径向/m | 切向/m | 法向/m | 三维坐标/m | 时钟/ns | ||
| 08 | 03:59:44 | 1.543 | 0.435 | 0.259 | 1.624 | 2.65 | 0.087 | 0.300 | 0.233 | 0.109 | 2.08 |
| 04:00:00 | 1.329 | 2.471 | 0.539 | 2.857 | 3.73 | 0.111 | 0.579 | 0.443 | 0.454 | 2.08 | |
| 22 | 11:59:44 | 1.012 | 0.441 | 0.591 | 1.253 | 1.51 | 0.035 | 0.271 | 0.262 | 0.183 | 0.37 |
| 12:00:00 | 1.086 | 1.007 | 1.233 | 1.927 | 2.02 | 0.045 | 0.504 | 0.292 | 0.316 | 0.37 | |
对32颗卫星第121~127天非整点时刻数据块进行质量评估。PRN27第121~127天精密星历全部标记不正常(轨道坐标标记为“0”、钟差标记为“999 999.999 999”),故以下统计图无PRN27数据;被标记不正常的精密星历还有PRN30第124、126全天数据和PRN32第124全天数据。
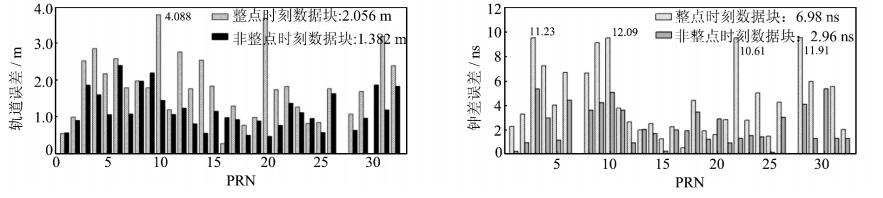
以PRN07为参考卫星,对第122天所有卫星非整点时刻数据块进行质量分析,图 5是两种时刻数据块轨道和钟差误差的RMS直方图。其中,PRN30整点时刻数据块的钟差误差有96%历元结果大于20 ns,认为该数据块为粗差并剔除。为更好显示图形,对轨道误差大于4 m、钟差误差大于10 ns的卫星用实际数值在图上标明。
|
| 图 5 所有GPS卫星122天非整点时刻与整点时刻数据块轨道和钟差误差RMS Fig. 5 Orbit and Clock RMS Errors of Non-integer-hour and Integer-hour Data Blocks on DOY 122 |
从图 5看出,23颗卫星非整点时刻数据块轨道误差小于1.5 m;相反,有19颗卫星整点时刻数据块轨道误差超过1.5 m,其中,PRN10、PRN20和PRN31轨道误差大于3 m。所有卫星非整点时刻数据块的轨道精度为1.382 m,优于整点时刻数据块的2.056 m。钟差方面,大多数卫星非整点时刻数据块钟差误差RMS优于3 ns,最大值为PRN30的 5.32 ns;而有11颗卫星整点时刻数据块钟差精度低于5 ns,其中,PRN03、PRN10、PRN22和PRN28钟差误差超过了10 ns。就所有卫星,非整点时刻数据块的钟差误差RMS为2.96 ns优于整点时刻数据块的6.89 ns。
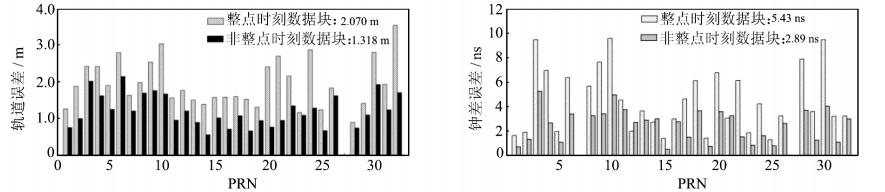
图 6为连续7 d所有GPS卫星非整点时刻与整点时刻数据块轨道和钟差的误差RMS,同样以PRN07为参考星。其中,PRN30第121和122两天数据判定为粗差。对所有卫星按式(5)进行精度计算,非整点时刻数据块的轨道精度为1.381 m,优于整点时刻数据块的2.070 m;非整点时刻数据块的钟差精度为2.89 ns,优于整点数据块的5.43 ns。
|
| 图 6 所有GPS卫星121~127天非整点时刻与整点时刻数据块轨道和钟差误差RMS Fig. 6 Orbit and Clock RMS Error of Non-integer-hour and Integer-hour Data Blocks from DOY 121 to 127 |
本文首先描述了GPS广播星历非整点时刻数据的三种形式,对2013年121~127天的广播星历数据块进行统计分析发现,非整点时刻数据块占所有星历数据块的16.0%。以IGS精密产品为参考,本文重点研究了占7.7%的第二类非整点时刻数据块,结果表明非整点时刻数据块的轨道精度为1.381 m,优于整点时刻的2.070 m;非整点时刻数据块的时钟精度为2.89 ns,优于整点时刻的5.43 ns。因此,当非整点时刻与整点时刻数据块同时出现时,建议用户使用非整点时刻数据块。
后续工作将围绕GPS广播星历非整点时刻和整点时刻数据块对定位的影响展开。本文第一章描述了使用RTCM 3.1版本改正数进行卫星轨道、时钟误差改正的情况,该类型改正数的应用为实时PPP;同时,对于使用RTCM 2.3版本改正数进行距离观测值改正的应用为实时差分定位。探究不同时刻星历数据块对这两种定位模式的影响是今后的研究重点。此外,本文的结论也可为今后GNSS接收机处理非整点时刻星历数据块提供参考。
| [1] | Noureldin A, Karamat B, Georgy J. Fundamentals of Inertial Navigation, Satellite-Based Positioning and Their Integration[M].NY:Springer, 2013 |
| [2] | Li Zhenghang, Ding Wenwu, Li Zhao. Error Analysis of Orbit Determined by GPS Broadcast Ephemeris[J].Journal of Geodesy and Geodynamics, 2008, 28(1):50-54(李征航, 丁文武, 李昭. GPS 广播星历的轨道误差分析[J].大地测量与地球动力学, 2008, 28(1):50-54) |
| [3] | IGSCB. GPS Satellite Orbit and Clock Product Summary Updated for 2009[OL]. http://igscb.jpl.nasa.gov/components/prods.html, 2013 |
| [4] | Heng Liang, Gao Xinxin, Todd W, et al. GPS Ephemeris Error Screening and Results for 2006-2009[C]. The 2010 International Technical Meeting of the Institute of Navigation(ION ITM 2010), San Diego, CA, 2010 |
| [5] | Estey L. Change in TEQC's Tests for Questionable GPS Navigation Messages[OL].http://postal.unavco.org/pipermail/teqc/2012/001328.html, 2012 |
| [6] | Roulston A, Talbot N, Zhang K. An Evaluation of Various GPS Satellite Ephemerides[C]. The 13th International Technical Meeting of the Satellite Division of the Institute of Navigation(ION GPS 2000), Salt Lake City, 2000 |
| [7] | Fu Xiaofeng, Wu Meiping. Optimal Design of Broadcast Ephemeris Parameters for a Navigation Satellite System[J].GPS Solutions, 2012, 16(4):439-448 |
| [8] | Jefferson D C, Bar-Sever Y E. Accuracy and Consistency of Broadcast GPS Ephemeris Data[C].The 13th International Technical Meeting of the Satellite Division of the Institute of Navigation(ION GPS 2000), Salt Lake City, 2000 |
| [9] | Warren D L M, Raquet J F. Broadcast vs Precise GPS Ephemerides:A Historical Perspective[J].GPS Solutions, 2003, 7(3):151-156 |
| [10] | Guo Fei, Zhang Xiaohong, Li Xingxing, et al. Precision Analysis on Orbit and Clock of GPS Satellites Broadcast Ephemeris[J].Geomatics and Information Science of Wuhan University, 2009, 34(5):589-592(郭斐, 张小红, 李星星, 等. GPS 系列卫星广播星历轨道和钟的精度分析[J].武汉大学学报·信息科学版, 2009, 34(5):589-592) |
| [11] | Cohenour C, Graas F. GPS Orbit and Clock Error Distributions[J].Navigation, 2011, 58(1):17-28 |
| [12] | Chris R. Principles and Practice of GPS Surveying[OL].http://www.gmat.unsw.edu.au/snap/gps/gps_survey/principles_gps.html , 1999 |
| [13] | Heng Liang, Gao Xinxin, Todd W, et al. Statistical Characterization of GPS Signal-in-space Errors[C]. The 2011 International Technical Meeting of the Institute of Navigation(ION ITM 2011), San Diego, CA, 2011 |
| [14] | Guo Jinyun, Hwang Cheinway, Tseng Zipang, et al. Determination of High-Rate Clock Corrections for GPS Satellites from Observations of IGS Stations[J].Geomatics and Information Science of Wuhan University, 2008, 33(7):706-709(郭金云, 黄金维, 曾子榜, 等.基于IGS跟踪站的高频GPS卫星时钟改正确定[J].武汉大学学报·信息科学版, 2008, 33(7):706-709) |
| [15] | Huang Guanwen, Zhang Qin, Xu Guochang, et al. IGS Precise Satellite Clock Model Fitting and ITS Precision by Using Spectral Analysis Method[J].Geomatics and Information Science of Wuhan University, 2008, 33(5):496-499(黄观文, 张勤, 许国昌, 等. 基于频谱分析的IGS精密星历卫星钟差精度分析研究[J].武汉大学学报·信息科学版, 2008, 33(5):496-499) |
| [16] | Griggs E, Kursinski E R, Akos D. An Investigation of GNSS Atomic Clock Behavior at Short Time Intervals[J].GPS Solution, 2013:1-10 |
| [17] | Jefferson D C, Bar-Sever Y E. Accuracy and Consistency of Broadcast GPS Ephemeris Data[C]. Proceedings of the 13th International Technical Meeting of the Satellite Division of the Institute of Navigation(ION GPS 2000), San Diego, CA, 2000 |
| [18] | Montenbruck O, Steigenberger P, Hauschild A. Broadcast Versus Precise Ephemerides:A Multi-GNSS Perspective[J].GPS Solutions, 2014:1-13 |
| [19] | Jia Ruixi, Li Xiaoyu, Xia Changfeng, et al. Broadcast Ephemeris Accuracy Analysis for GPS Based on Precise Ephemeris[J].Applied Mechanics and Materials, 2014, 602:3 667-3 670 |
| [20] | Park J K, Jung K Y. Accuracy Analysis of Influences by Satellite Ephemeris[J].Contemporary Engineering Sciences, 2014, 7(24):1 397-1 405 |
| [21] | Wang Dongjin, Huang Zhigang, Li Rui. Integrity Analysis of GPS Signal-in-Space Error[C]. China Satellite Navigation Conference(CSNC) 2013 Proceedings, Wuhan, China, 2013 |
 2015, Vol. 40
2015, Vol. 40



