文章信息
- 张明, 刘晖, 丁志刚, 汤晟佳, 范城城
- ZHANG Ming, LIU Hui, DING Zhigang, TANG Shengjia, FAN Chengcheng
- 基于序贯平差的长距离基准站间模糊度快速固定
- Fast Ambiguity Resolution Between Long-Range Base Stations Based on Sequential Adjustment
- 武汉大学学报·信息科学版, 2015, 40(3): 366-371
- Geomatics and Information Science of Wuhan University, 2015, 40(3): 366-371
- http://dx.doi.org/10.13203/j.whugis20130628
-
文章历史
- 收稿日期:2013-10-30
2. 山东北斗华宸导航技术有限公司, 山东 淄博, 255000;
3. 中国地震台网中心, 北京, 100045;
4. 武汉大学测绘遥感信息工程国家重点实验室, 湖北 武汉, 430079
2. Shandong Comp Star Navi Technology Co., Ltd, Zibo 255000, China;
3. China Earthquake Networks Center, Beijing 100045, China;
4. State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China
长距离基准站间模糊度固定是网络RTK的关键技术之一,直接决定网络RTK系统的初始化速度和可靠性。由于基准站间距离远,误差相关性低,组成双差观测值后电离层、对流层残差依然具有较大影响,导致模糊度固定困难。
序贯平差方法是长距离基准站间模糊度固定中的常用方法,采用序贯平差方法求解观测方程组,具有大量的多余观测,而且随着观测时间的增加,多余观测量逐步累积,这对于提高模糊度浮点解精度及模糊度固定的可靠性是十分有利的[1, 2]。
文献[3]仅给出了参数不变的序贯平差公式。但由于周跳的问题,观测卫星、电离层和对流层的变化以及模糊度的固定,这些都会导致待估参数的变化,因此参数不变的序贯平差公式不适用于网络RTK系统。
黄维彬分别推导了参数增加和减少时的序贯平差公式,但没有考虑参数增加和减少同时出现的情况,公式推导过程比较复杂[4];魏子卿提出了参数消去法,在序贯平差过程中,可以将不感兴趣的多余参数消去,并将前后两组法方程相加组成新的法方程,但并未说明法方程相加的原理[5];沈雪峰对参数变化的序贯平差进行了说明,指出了参数增加时法方程的处理思路,但未给出公式推导过程[6];赵长胜推导了具有相关观测量的可变参数序贯平差公式,但未总结序贯平差递推规律[7]。序贯平差的核心思想是将前一历元的平差结果作为虚拟观测方程与当前历元观测方程联合平差,借鉴这一思想,本文推导了参数变化的序贯平差公式。
模糊度固定后,为了估计剩余参数实现滤波的递推,需要将固定的模糊度带入原方程中重新平差。序贯平差不需要存储历史观测值,节省了存储空间并提高了计算效率,但这也导致模糊度固定后法方程更新困难。魏子卿直接从观测方程出发推导了模糊度固定后的法方程更新公式[5]。但在序贯平差过程中,类似整体平差的观测方程是不存在的。本文虚构了与法方程等价的观测方程,推导了模糊度固定后法方程的更新公式。
1 参数变化的序贯平差
对于序贯平差而言,不需要存储大量观测值,也不需要求解大规模矩阵,因此,可以节省存储空间并提高计算效率。参数不随时间变化的序贯平差,有时又称为静态卡尔曼滤波[3]。文献[3]给出了参数不变的序贯平差公式及详细的推导过程。
对于网络RTK而言,由于周跳不可避免,现有的周跳修复算法不能保证修复结果完全正确,更为谨慎的做法是当卫星发生周跳后,重新估计其模糊度;随着卫星的运动,观测卫星会发生变化;观测过程中电离层延迟和对流层延迟也会发生变化,如果对电离层和对流层进行估计,待估参数也会相应改变;由于宽巷模糊度波长约为86 cm,相对于窄巷模糊度更容易固定,因此,通常优先固定宽巷模糊度。此外,高度角高的卫星和观测弧段长的卫星其模糊度精度一般更高,通常也会被优先固定。这些情况都会导致参数发生变化,因此,参数不变的序贯平差公式并不适用于网络RTK。
序贯平差的核心思想是将前一历元平差的结果作为虚拟观测方程,与当前历元观测方程联合平差。借鉴这一思想,本文推导了参数变化的序贯平差公式。
可将待估参数分为3类:第一类是旧参数,只出现在前一历元中;第二类是保留参数,同时出现在前一历元和当前历元中;第三类是新参数,只出现在当前历元中。这里我们考虑3种类型参数均出现的情况。
第一个历元的观测方程为:
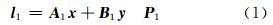
第二个历元的观测方程为:
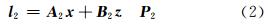
式中,l 1、 l 2为观测值向量,相互之间不具有相关性; A 1、B 1、 A 2、 B 2为系数阵; x 、 y 、 z 为待估参数向量; P 1、 P 2为观测值权阵。
从观测方程中可以发现,x 为保留参数,y 为旧参数,z 为新参数,我们对参数 y 不感兴趣,因此在第二个历元中只求解参数 x 、 z 。
若第一个历元的法方程为:

将式(3)改写为:
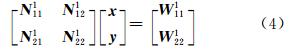
将式(4)展开可得:
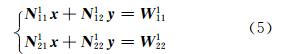
对式(5)进行变形,将 y 用 x 表示:

将式(6)带入式(5),经变形可得 x 的法方程为:
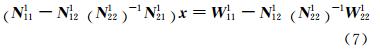
式(4)~式(7)变形过程可参考文献[8],只需证明第一个历元x 的平差结果与式(7)的解相同,即可证明式(7)就是 x 的法方程。
令:
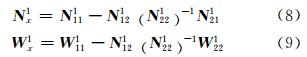
可将式(7)改写为:

第一个历元 x 的解为:
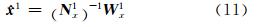
其方差协方差阵为:

将 x 的解写成虚拟观测方程的形式,与第二个历元观测方程组成观测方程组:
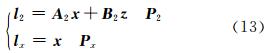
其中,
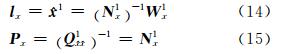
若该观测方程组对应的法方程为:

可以证明:
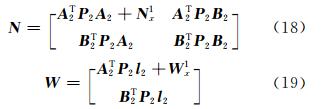
求解此法方程,即可得到 x、z 的序贯平差解。
此即为参数变化的序贯平差公式,此公式完全可以满足编程的需要,不需要进一步变形。从以上公式可以看出,参数变化的序贯平差递推过程,其本质是将前一历元法方程与当前历元法方程相加。不过前提是从前一历元的法方程中,提取出保留参数的法方程。需要注意的是,在法方程相加过程中,要确保前后历元保留参数顺序一致。对于参数不变的序贯平差,该公式同样适用,具有通用性。
2 法方程更新
部分或全部模糊度固定后,通常需要将模糊度回带到原方程中重新平差,固定剩余的模糊度或实现滤波递推。但是在序贯平差过程中,通常不会保留历史观测值。即使我们存储所有历元的观测值,重新组建观测方程并平差,这种方法的效率也极低。但我们可以直接更新法方程,获得等价的结果。
若序贯平差后得到的法方程为:

式中,x对应未固定的参数向量;y对应固定的模糊度参数向量。
虽然我们不具有类似整体平差的观测方程,但是可以虚构一个与法方程等价的观测方程。该方程实际上就是采用整体平差方法解算时对应的观测方程,因此是一定存在的:
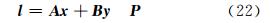
式中,l 为观测值向量; A、B 分别为系数阵; P 为观测值权阵。
则:
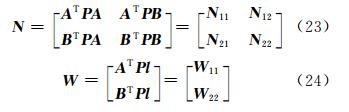
若 y 固定为a y,由于其变为常数后不再具有随机特性,因此可将原观测方程进行变换,变换后新的观测值向量的权阵不变:
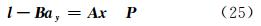
对应的法方程为:

其中,
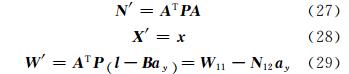
将式(27)~式(29)带入到式(26)中,得到更新后的法方程为:

从以上公式可以看出,模糊度固定后,不需要重新组建观测方程。原法方程中包含了用于更新法方程的全部信息,从原法方程中提取出与固定模糊度和未固定参数相关的矩阵,即可实现法方程的更新。
3 观测模型
本文采用非组合模型,若基准站为 A、B卫星 i为参考卫星,对于卫星j的双差观测方程为:
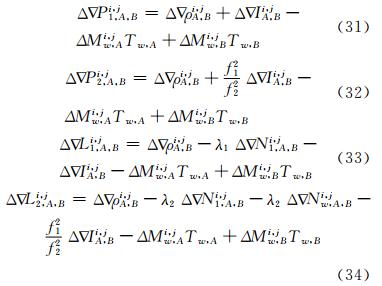
式中,Δ 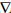 P1,A,Bi,j、Δ
P1,A,Bi,j、Δ 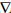 P2,A,Bi,j、Δ
P2,A,Bi,j、Δ 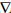 L1,A,Bi,j、Δ
L1,A,Bi,j、Δ 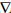 L2,A,Bi,j为双差伪距和相位观测值;Δ
L2,A,Bi,j为双差伪距和相位观测值;Δ 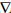 ρA,Bi,j为双差卫地距;f1、f2为L1、L2的频率;Δ
ρA,Bi,j为双差卫地距;f1、f2为L1、L2的频率;Δ 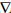 IA,Bi,j为双差电离层;ΔMi,jw,A、ΔMw,Bi,j分别为测站A、B的单差对流层湿延迟投影函数;Tw,A、Tw,B分别测站A、B天顶对流层湿延迟;Δ
IA,Bi,j为双差电离层;ΔMi,jw,A、ΔMw,Bi,j分别为测站A、B的单差对流层湿延迟投影函数;Tw,A、Tw,B分别测站A、B天顶对流层湿延迟;Δ 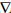 N1,A,Bi,j为双差窄巷模糊度;Δ
N1,A,Bi,j为双差窄巷模糊度;Δ 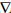 Nw,A,Bi,j为双差宽巷模糊度。
Nw,A,Bi,j为双差宽巷模糊度。
对于长距离网络RTK而言,电离层和对流层是影响模糊度固定的最大误差源。本文将电离层延迟作为参数估计,对流层干延迟采用模型改正,对于湿延迟,将天顶湿延迟投影到斜路径方向,并将天顶湿延迟作为分段常数估计。对流层模型采用Unb3模型[9],投影函数采用GMF[10]。为了提高模糊度浮点解精度,还需要改正天线PCO、天线PCV、相位缠绕、地球自转效应等误差[11, 12, 13, 14, 15]。此外,本文采用高度角定权策略[16]。
4 算例分析
为了对公式进行验证,本文处理了6个测站共15条基线数据。测站位于山东某地,观测时间为2010-03-26,数据采样间隔为30 s,接收机型号为TPS NET-G3。测站坐标精确已知,基线平均长度约为123 km。
测站分布如图 1所示。

|
| 图 1 测站分布图,基线长度单位为km Fig. 1 The Distribution of Stations,the Unit of Baseline Length is km |
由于周跳的存在,不同卫星观测弧段长度不同,通常观测弧段长的卫星模糊度具有更高精度。因此,采用部分搜索策略,将卫星按照观测弧段长度分组,优先搜索观测弧段长的卫星。先搜索宽巷模糊度,宽巷模糊度固定后,再搜索对应卫星的窄巷模糊度。
本文算例使用LAMBDA方法[17, 18],Ratio阈值设为3。
当搜索的模糊度为1维时,直接取整固定,取整成功率阈值设为99.9%,取整成功率计算公式可参考文献[16, 19],模糊度整数解与浮点解的差值需满足下式:
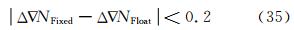
此外,为了进一步提高模糊度固定的正确率,模糊度固定前后单位权方差的比值需满足下式[20]:

序贯平差单位权方差的计算方法可以参考文献[21]。
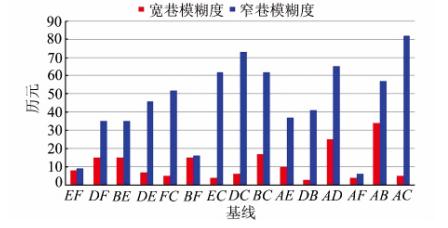
图 2为宽巷模糊度和窄巷模糊度固定速度,基线长度从左到右依次增大。从图中可以看出,对于宽巷模糊度,模糊度固定速度与基线长度没有严格的相关性。主要原因是宽巷模糊度主要由MW组合观测值决定,不受电离层、对流层、卫地距、基线长度的影响。
随着基线长度的增加,窄巷模糊度固定速度呈下降趋势。这是因为随着基线长度增加,轨道误差、对流层以及其他误差的残差增加,导致窄巷模糊度固定难度增大。
|
| 图 2 模糊度固定速度 Fig. 2 The AR Speed |
宽巷模糊度比窄巷模糊度的固定速度快,经统计,宽巷模糊度的平均固定速度为11.5个历元,窄巷模糊度的平均固定速度为45.2个历元。这是由于宽巷模糊度的波长更长(约为86 cm),更容易固定,在模糊度搜索过程中,宽巷模糊度也被优先搜索。

|
| 图 3 模糊度固定正确率 Fig. 3 The AR Correct Rate |

式中,Pc为模糊度固定的正确率;nc为正确固定的模糊度数量;N为模糊度总数。
从图 3可以看出,所有基线的宽巷模糊度全部固定正确,对于窄巷模糊度,除了AF基线有一颗卫星固定错误,其他基线全部固定正确。这是因为宽巷模糊度波长更长,固定的可靠性和正确率也更高。
5 结 语
一般文献中仅给出了参数不变的序贯平差公式,该公式不适用于网络RTK。借鉴序贯平差公式推导过程中虚拟观测方程思想,本文推导了参数变化的序贯平差公式。公式表明,对于参数变化的序贯平差而言,其法方程等于前一历元法方程与当前历元法方程之和。该公式考虑了参数增加和减少的情况,也适用于参数不变的情况,具有通用性。
由于序贯平差不保留历史观测值,无法像整体平差一样重新组建观测方程,导致法方程更新困难。本文虚构了与法方程等价的观测方程,推导了模糊度固定后的法方程更新公式。
本文结合模糊度部分搜索算法和多种模糊度验证手段,实现了模糊度的快速固定。宽巷模糊度和窄巷模糊度固定的平均速度分别为11.5、45.2个历元,对应的时间分别为5.75 min、22.6 min。证明本文推导的公式对于长距离基准站间模糊度快速固定,是正确且十分有效的。
| [1] | Han S.Carrier Phase-Based Long-Range GPS Kinematic Positioning[R]. Unisurv ReportNo.S-49, School of Geomatic Engineering, the University of New South Wales, 1997 |
| [2] | Han Shaowei, Rizos C. Comparing GPS Ambiguity Resolution Techniques[J].GPS World, 1997, 8(10):54-61 |
| [3] | Surveying Adjustment Term, School of Geodesy and Geomatics, Wuhan University. Generalized Surveying Adjustment Edition[M].2nd Edition. Wuhan:Wuhan Universtity Press, 2000(武汉大学测量平差学科组. 误差理论与测量平差基础(第二版)[M].武汉:武汉大学出版社, 2000) |
| [4] | Huang Weibin.Modern Adjustment Theory and Its Application[M].Beijing:People's Liberation Army, 1992(黄维彬. 近代平差理论及其应用[M].北京:解放军出版社, 1992) |
| [5] | Wei Ziqin, Ge Maorong.The Mathematical Model of GPS Relative Positioning[M].Beijing:Surveying and Mapping Press, 1998(魏子卿, 葛茂荣. GPS相对定位的数学模型[M].北京:测绘出版社, 1998) |
| [6] | Shen Xuefeng, Gao Chengfa. An Approach for Ambiguity Resolution Based on Improved Sequential Adjustment Suitable for Medium-Long Baseline[J].Science of Surveying and Mapping, 2012, 37(2):158-160(沈雪峰, 高成发, 潘树国. 一种序贯平差中长基线模糊度的解算方法[J].测绘科学, 2012, 37(2):158-160) |
| [7] | Zhao Changsheng. Variable Parameters Sequential Adjustment with Relevant Observation[J].Bulletin of Surveying and Mapping, 2009(11):21-23(赵长胜. 具有相关观测量的可变参数序贯平差[J].测绘通报, 2009(11):21-23) |
| [8] | Xu Guochang. GPS Theory, Algorithms and Applications[M].2nd Edition. Beijing:Tsinghua University Press, 2011(许国昌. GPS理论、算法与应用(第二版)[M].北京:清华大学出版社, 2011) |
| [9] | Leandro R F, Santos M C, Langley R B. UNB Neutral Atmosphere Models:Development and Performance [C]. ION NTM 2006, Monterey, California, USA, 2006 |
| [10] | Boehm J, Niell A, Tregoning P, Schuh H. Global Mapping Function(GMF):A New Empirical Mapping Function Based on Data from Numerical Weather Model Data[J].Geophysical Research Letters, 2006, 33, L07304, doi:10.1029/2005 GL 025546 |
| [11] | McCarthy D.D. IERS Standards[P]. IERS Technical Note 3, IERS, 1989 |
| [12] | IERS. IERS Conventions[R]. International Earth Rotation Service(IERS), Central Bureau, 1996 |
| [13] | Kouba J.A Guide to Using International GNSS Service(IGS) Products[OL].http://igscb.jpl.nasa.gov/igscb/resource/pubs/usingIGSproductsVer21.pdf, 2009 |
| [14] | Li Zhenghang, Huang Jinsong.GPS Survey and Data Processing[M].2nd Edition. Wuhan:Wuhan University Press, 2010(李征航, 黄劲松. GPS测量与数据处理(第二版)[M].武汉:武汉大学出版社, 2010) |
| [15] | Li Zhenghang, Zhang Xiaohong. New Techniquesand Precise Data Processing Methods of Satellite Navigation and Positioning[M].Wuhan:Wuhan University Press, 2009(李征航, 张小红. 卫星导航定位新技术及高精度数据处理方法[M].武汉:武汉大学出版社, 2009) |
| [16] | Ge Maorong, Gendt G, Rothacher, M et al.Resolution of GPS Carrier-phase Ambiguities in Precise Point Positioning(PPP) with Daily Observations[J].J Geod, 2008, 82:389-399, doi:10.1007/s00190-007-0187-4 |
| [17] | Jonge de P J, Tiberius C C J M. Integer Ambiguity Estimation with the LAMBDA Method[C]. Proceedings IAG SymposiumNo.115, GPS Trends in Precise Terrestrial, Airborne and Spaceborne Applications, XXI General Assembly of IUGG, Boulder, CO, 1995 |
| [18] | Teunissen P J G. A New Method for Fast Carrier Phase Ambiguity Estimation[C]. Proceedings IEEE Position, Location and Navigation Symposium PLANS'94, Las Vegas, NV, 1994 |
| [19] | Dong Danan. The Horizontal Velocity Fieldin Southern Californa from a Combination of Terrestrial and Sapce-Geodetic Data[D].Cambridge:Massachusetts Institute of Technology, 1993 |
| [20] | Dach R, Hugentobler U, Fridez P. Michael Meindl[R]. Bernese GPS Software Version 5.0, 2007 |
| [21] | Tao Benzao. About the Formula of the Unit Weight Variance[J].Bulletin of Surveying and Mapping, 1998(9):5-6(陶本藻. 关于单位权方差公式[J].测绘通报, 1998(9):5-6) |
| [22] | Zhu Huizhong, Liu Jingnan, Tang Weiming, et al. An Algorithm of Instantaneous Double Difference Ambiguity Resolution for Long-Range Reference Stations of Network RTK[J].Geomatics and Information Science of Wuhan University, 2012, 37(6):688-692(祝会忠, 刘经南, 唐卫明, 等.长距离网络RTK参考站间双差模糊度快速解算算法[J].武汉大学学报·信息科学版, 2012, 37(6):688-692) |
| [23] | Yan Ziping, Ding Lele, Huang Enxing, et al. A New Method of Ambiguity Resolution in Network RTK Between Reference Station[J].Geomatics and Information Science of Wuhan University, 2013, 38(3):295-323(鄢子平, 丁乐乐, 黄恩兴, 等.网络RTK基准站间模糊度固定新方法[J].武汉大学学报·信息科学版, 2013, 38(3):295-323) |
| [24] | Tang Weiming, Liu Jingnan, Shi Chuang, et al. Three Steps Method to Determine Double Difference Ambiguities Resolution of Network RTK Reference Station[J].Geomatics and Information Science of Wuhan University, 2007, 32(4):305-308(唐卫明, 刘经南, 施闯, 等.三步法确定网络RTK基准站双差模糊度[J].武汉大学学报·信息科学版, 2007, 32(4):305-308) |
 2015, Vol. 40
2015, Vol. 40



