文章信息
- 邹贤才, 李建成, 衷路萍, 徐新禹
- ZOU Xiancai, LI Jiancheng, ZHONG Luping, XU Xinyu
- 动力法校准GRACE星载加速度计
- Calibration of the Accelerometers Onboard GRACE with the Dynamic Method
- 武汉大学学报·信息科学版, 2015, 40(3): 357-360
- Geomatics and Information Science of Wuhan University, 2015, 40(3): 357-360
- http://dx.doi.org/10.13203/j.whugis20130269
-
文章历史
- 收稿日期:2013-06-24
星载加速度计是卫星重力测量中分离保守力和非保守力的关键设备,其校准在CHAMP任务期间就得到了广泛研究[1, 2, 3, 4],在相关科学应用中也具有重要价值[5]。目前,国际上有机构发布校准参数,但明确声明这些结果都只能作为参考,独立处理卫星重力数据仍然需要自行估计[6]。国内关于GRACE加速度计校准的公开研究成果不多,其中包括能量法[7]。作为卫星重力场建模主要方法之一的动力法,可以避免能量法中所需的速度内插,是一种很好的校准方法。但国内的工作只在仿真研究的层面上进行过探讨[8]。本文利用动力法处理GRACE任务实测数据,比较不同校准方案,为后续重力场模型解算提供科学指导。
1 基本方法与数据
本文选择普遍采用的比例-偏差模型[8, 9, 10]作为加速度计校准数学模型,所用精密轨道由德国慕尼黑工业大学Svehla博士提供,精度达到0.06 m左右[11],采样间隔为30 s。卫星精密轨道可以表示为:

式中,r 为地心到卫星的向径; r 0和 v 0为卫星的初始位置和初始速度; ACC(accelerometer)表示 卫星加速度计校准参数; C 和 S 为重力场模型参数向量。式(1)表示如果已知卫星初始状态和它的力学模型(保守力和加速度计提供的非保守力),则卫星轨道确定。星间距离变率 可以表示为:
可以表示为:
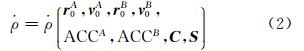
式中,上标A和B分别表示构成星间观测的卫星。
对于动力法,通过计算状态转移矩阵和参数敏感矩阵,可以获得卫星轨道和星间距离变率对参数的偏导数[12],从而可以用最小二乘平差的方法来逐步逼近待估参数。式(2)中的重力场模型参数 C 、 S 是全局参数。精密轨道和星间距离变率数据联合处理时,两颗卫星的初始状态 r 0A、 v 0A、 r 0B、 v 0B是弧段内的局部参数。文献[13, 14]对参数的类似性质做过探讨,这些算法设计问题不属于本文的研究范畴,不再赘述,但在处理时需要特别注意。
2 动力法校准结果 2.1 计算方案
本文处理了精密轨道一个月的数据,设计了以下两个方案。
方案1 待估参数包括完全到100阶次的重力场模型参数、轨道初值和加速度计校准参数;
方案2 为了研究固定重力场模型对校准结果的影响,选择EGM2008截断至360阶的模型作为参考场,只估计轨道初值和校准参数。
2.2 结果分析
首先给出方案1的整体解算结果,SRF中3个方向的比例系数及其精度见表 1。
| SRF中的坐标方向 | GRACE-A | GRACE-B | ||
| 比例系数 | 精度 | 比例系数 | 精度 | |
| X | 0.957 9 | ±0.000 1 | 0.943 0 | ±0.000 1 |
| Y | 0.987 0 | ±0.007 1 | 1.090 9 | ±0.008 0 |
| Z | 0.939 6 | ±0.000 4 | 0.936 3 | ±0.000 4 |
表 1给出的比例系数精度要高于GRACE手册的推荐值的对应指标[6]。偏差参数的校准结果如图 1和图 2所示。注意,为了便于在同一幅图中比较其变化趋势,将偏差结果均进行一定的等比例放大,使结果分布在±10 m·s-2。从图中可以看出,两颗卫星的SRFx和SRFy方向偏差系数非常稳定,这是与能量法校准结果的明显区别[7]。GRACE卫星的SRFx和SRFy方向分别为沿迹方向和轨道面法向,其中沿迹方向主要为大气阻力,轨道面法向是最不敏感轴,变化应该比较平稳。SRFz方向主要受光压和反照压的影响,与卫星的空间位置和姿态有关,变化幅度大,并呈现出一定的周期性。上述偏差参数的变化趋势符合GRACE卫星的工作环境。

|
| 图 1 GRACE-A加速度计偏差参数校准结果 Fig. 1 Calibration for the Biases of Accelerometer of GRACE-A |

|
| 图 2 GRACE-B加速度计偏差参数校准结果 Fig. 2 Calibration for the Biases of Accelerometer of GRACE-B |
由于GRACE官方发布的校准结果只有参考意义,为了进一步验证校准结果,我们对恢复的100阶次重力场模型进行了精度验证。从图 3可以看出,该模型的阶方差与Kaula准则吻合得很好,误差阶方差变化平稳,且均小于阶方差。

|
| 图 3 100阶次重力场模型阶方差和误差阶方差 Fig. 3 Signal/Error Degree Variance of the EGM Completed to Degree and Order 100 |
为了进一步验证该模型的精度,我们作出了大地水准面的阶误差分布图,如图 4所示。100阶模型大地水准面累积误差为4 cm,CSR发布的月重力场模型GX-OG-_2-GSM+CSR-GSM-2_0030_2003182-2003212_UTCSR_0000_0001对应的指标为6 cm,本文的模型在这一指标上更优。综合以上分析,其校准结果是可靠的。

|
| 图 4 大地水准面阶误差分布图 Fig. 4 Error Per Degree of the Geoid |
下面采用方案2,固定重力场模型进行校准。为了评估这种策略带来的影响,我们先给出比例系数的校准结果和精度,参见表 2。
| SRF中的坐标方向 | GRACE-A | GRACE-B | ||
| 比例系数 | 精度 | 比例系数 | 精度 | |
| X | 0.956 1 | ±0.000 1 | 0.940 9 | ±0.000 1 |
| Y | 1.006 6 | ±0.008 3 | 0.949 8 | ±0.009 5 |
| Z | 0.931 0 | ±0.000 4 | 0.927 4 | ±0.000 4 |
比较表 1和表 2,方案1和方案2的比例系数差异主要体现在SRFy方向上,这也是校准中精度最差的方向。原因在于SRFy方向上的非保守力对轨道的影响没有其他两个方向敏感[14],因此,利用轨道估计SRFy方向的校准参数精度也最差,要想获得更稳定的结果应需要更长时间的观测数据或其它约束。方案1和方案2对校准结果的影响,还可以利用分别获得的校准参数计算卫星受到的非保守力,分析两者之间的差异。本文分析了1 d数据,如表 3所示。
| 双星SRF中的坐标方向 | 最小值 | 最大值 | 平均值 | 中误差 | |
| X | GRACE-A | -1.469 95×10-9 | -6.698 90×10-10 | -9.014 55×10-10 | 9.220 99×10-10 |
| GRACE-B | -1.038 74×10-9 | -2.546 08×10-10 | -8.119 99×10-10 | 8.259 77×10-10 | |
| Y | GRACE-A | 2.087 96×10-9 | 5.490 68×10-9 | 4.420 20×10-9 | 4.435 53×10-9 |
| GRACE-B | 5.615 94×10-8 | 7.211 92×10-8 | 6.805 06×10-8 | 6.806 28×10-8 | |
| Z | GRACE-A | 2.316 66×10-9 | 4.863 47×10-9 | 3.794 09×10-9 | 3.814 25×10-9 |
| GRACE-B | 5.840 98×10-9 | 8.976 61×10-9 | 7.878 79×10-9 | 7.893 64×10-9 | |
从表 3可以看出,相对加速度计测量精度(敏感轴约3×10-10m·s-2,非敏感轴约10-9m·s-2),两种方案之间存在明显差异。特别是GRACE-B卫星SRFy方向,达到10-8m·s-2量级。前面已经分析了SRFy方向难以获得稳定校准结果的原因,此处精度最差的也正好出现在该方向。还有一个显著特点就是方案间的非保守力校准结果存在系统性趋势,差值恒正或恒负,而不是在零值附近震荡。因此,同时解算重力场模型的方案才能获得可靠的加速度计校准结果。
3 结 语
本文研究了GRACE星载加速度计的动力法校准,在没有标准参考结果的情况下,对校准结果的趋势进行了分析,认为该趋势符合加速度计运行环境。本文解算的100阶次重力场模型信号/误差阶方差分布合理,100阶次的大地水准面累积误差4 cm,优于CSR发布的同期月重力场模型,进一步验证了结果的可靠性和准确性。在固定重力场模型的情况下获得的非保守力结果与整体解算结果的差异最高可达10-8m·s-2量级,说明严密的加速度计校准结果应该通过与重力场模型及其他动力学相关参数的联合解算才能达到最优。本文工作是进一步开展大规模卫星重力场模型建模的基础,今后的工作重点要转移到高精度定轨及同解法的实用化上。校准成果还可用于有关空间环境的研究。
| [1] | Reubelt T, Austen G, Grafarend E W. Harmonic Analysis of the Earth's Gravitational Field by Means of Semi-continuous Ephemeris of a Low Earth Orbiting GPS-tracked Satellite, Case Study:CHAMP[J].Journal of Geodesy, 2003, 77:257-278 |
| [2] | Visser P N A M, Sneeuw N, Gerlach C. Energy Integral Method for Gravity Field Determination from Satellite Orbit Coordinates[J].Journal of Geodesy, 2003, 77:207-216 |
| [3] | Gerlach C, Sneeuw N, Visser P N A M, et al. CHAMP Gravity Field Recovery Using Energy Balance Approach[J].Advances in Geosciences, 2003, 31(1):73-80 |
| [4] | Han S C, Jekeli C, Shum C K. Efficient Gravity Field Recovery Using in Situ Disturbing Potential Observables from CHAMP[J].Geophys Res Letters, 2002, 29(16):1 789-1 794 |
| [5] | Chen Runjing, Peng Bibo, Gao Fan, et al. Analysis of Solar and Earth Albedo Radiation Pressure Models for GRACE on Their Performance[J].Geomatics and Information Science of Wuhan University, 2013, 38(12):127-130(陈润静, 彭碧波, 高凡, 等. GRACE卫星太阳光照与地球反照辐射压力模型的效果分析[J].武汉大学学报·信息科学版, 2013, 38(2):127-130) |
| [6] | Bettadpur S. Recommendation for a-priori Bias & Scale Parameters for Level-1B ACC Data[R]. JPL, Version 2, California, 2009 |
| [7] | Xu Xinyu, Li Jiancheng, Wang Zhengtao, et al. Calibration of GRACE Accelerometer Using Reference Gravity Field Model Based on Energy Balance Approach[J].Geomatics and Information Science of Wuhan University, 2008, 33(1):72-75(徐新禹, 李建成, 王正涛, 等. 利用参考重力场模型基于能量法确定GRACE加速度计校准参数[J].武汉大学学报·信息科学版, 2008, 33(1):72-75) |
| [8] | Zou Xiancai, Li Jiancheng, Luo Jia, et al. Calibration of Onboard Accelerometer by Dynamic Method[J].Geomatics and Information Science of Wuhan University, 2007, 32(12):1 152-1 155(邹贤才, 李建成, 罗佳, 等. 星载加速度计的动力法校准[J].武汉大学学报·信息科学版, 2007, 32(12):1 152-1 155) |
| [9] | Wu S, Kruizinga G. Algorithm Theoretical Basis Document for GRACE Level-1B Data Processing[R]. JPL D-27672, Version 1.0, California, 2004 |
| [10] | Case K, Kruizinga G, Wu S. GRACE Level 1B Data Product User Handbook, JPL D-22027, Version 1.3, California, 2010 |
| [11] | Svehla D, Rothacher M. Kinematic andReduced-Dynamic Precise Orbit Determination of Low Earth Orbiters[J].Advances in Geosciences, 2003(1):47-56 |
| [12] | Reigber C H. Gravity Field Recovery from Satellite Tracking Data[M].Sanso F, eds. Theory of Satellite Geodesy and Gravity Field Determination. Berlin:Springer, 1989:197-234 |
| [13] | Xiao Yun. Research on the Earth Gravity Field Recovery from Satellite-to-Satellite Tracking Data[D].Zhengzhou:Information Engineering University, 2006(肖云. 基于卫星跟踪卫星数据恢复地球重力场的研究[D].郑州:信息工程大学, 2006) |
| [14] | Zou Xiancai. Theory of Satellite Orbit and Earth Gravity Field Determination[D].Wuhan:Wuhan University, 2007(邹贤才. 卫星轨道理论与地球重力场模型的确定[D].武汉:武汉大学, 2007) |
 2015, Vol. 40
2015, Vol. 40


