文章信息
- 佘冰, 朱欣焰, 苏科华, 呙维, 徐晓
- SHE Bing, ZHU Xinyan, SU Kehua, GUO Wei, XU Xiao
- 道路网约束下的事件时空交互检验方法研究
- Test Methods for Space-time Interaction of Events Under Road Network Constraints
- 武汉大学学报·信息科学版, 2015, 40(3): 353-356
- Geomatics and Information Science of Wuhan University, 2015, 40(3): 353-356
- http://dx.doi.org/10.13203/j.whugis20130229
-
文章历史
- 收稿日期:2013-06-08
2. 武汉大学空天信息安全与可信计算教育部重点实验室, 湖北 武汉, 430079;
3. 武汉大学计算机学院, 湖北 武汉, 430079
2. Key Laboratory of Aerospace Information Security and Trusted Computing, Ministry of Education, Wuhan University, Wuhan 430079, China;
3. School of Computer, Wuhan University, Wuhan 430079, China
事件之间存在时空交互和聚集,是自然界普遍存在的现象。传统的时空交互检验方法包括Knox方法[1]、Mantel方法[2]以及Jacquez k 近邻方法[3],在犯罪学、人口学等多个学科被广泛应用[4, 5]。现实世界中,很多事件都是沿道路网进行分布,如城市管理事件中的一类主体事件——占道经营。对于此类沿网络空间分布的事件,使用二维平面的空间分析方法会错误的判断其聚集趋势[6, 7],从而误导后期决策。
近年来,很多二维平面分析方法都被扩展到了网络空间,如Voronoi图划分[8]、空间自相关分析[9]等。而在网络约束下的时空交互检验方法方面展开的理论应用研究则较少,Eckley等人对交通事故在道路网约束下的时空分布进行了Knox分析[10]。此外,事件的发生一般被作为二值型,即发生或未发生,而事件往往有轻重缓急之分,将事件的属性信息融入时空交互检验方法可以有效的增强时空交互检验方法的适应和表达能力。本文定义了网络约束下的空间权重矩阵,将事件的自身属性作为权值与之融合,从而把Baker’s修正Knox检验扩展到网络空间,并使用占道事件数据进行实验分析。
1 时空交互检验方法时空交互检验方法考虑时空相近的事件,并与无交互情况的原假设进行比较[11]。相比基于模型的方法,时空交互检验方法不依赖具体的模型假设,可以归为一类探索性的时空分析方法。
1.1 Knox检验Knox检验是最早也最为广泛使用的时空交互检验方法,其将 n个事件配成N=n(n-1)/2个事件对。定义空间距离矩阵 A s和时间距离矩阵 A t,先通过用户设定的空间和时间阈值进行逐元素二值标准化成为新的空间矩阵 B s与时间矩阵 B t:
Knox指数由此可表示为[12]:

Baker在Knox检验法的基础上引入原假设下的期望值,对Knox指数作出修正,由于其突破Knox指数的整数形式,可使得检验在统计显著性上更加有效[12]。Baker指数表达式如下[12]:

时空检验方法的统计结果显著性一般采用蒙特卡洛法进行伪p值的计算,通过对变换后的空间距离矩阵或者时间距离矩阵随机重排若干次来生成参考总体分布。
2 网络空间权重矩阵及时空交互检验计算
从时空检验方法的表达形式可以看出,检验指数的不同很大程度上取决于空间距离的定义。其都可以抽象为使用空间权重矩阵进行表达,而不同类型的空间权重矩阵则对应了不同的检验方法。本文侧重将时空检验方法中的距离矩阵在道路网约束条件下使用空间权重矩阵进行刻划。除去一般欧氏空间的局限性,时空交互检验方法一般只能运用于一元同质的事件数据[11]。而在实际应用过程中,事件往往有不同等级或程度划分,因此,将此种关系与纯粹的道路网距离关系相结合,可以使空间权重矩阵反映出语义信息与拓扑或距离空间相融合后的更丰富的关联关系。
2.1 网络空间权重矩阵构建空间权重矩阵常用于空间自相关的分析[13],且自相关指数也依赖于空间权重矩阵的计算方法[14]。定义无向无交叉网络 N=(V,L),其中节点集合V,边集合L。定义事件集合E={e1,…,en},事件由一个四元组表示:ei=<IDi,si,ti,αi >,分别表示该事件的编号、空间、时间以及加权值。定义网络约束下的空间权重矩阵 A Sn,矩阵元素 A Snij代表事件ei和ej的“接近性”。 A Sn有两种形式,一种是基于事件所在边之间是否有邻接关系的邻接法;另一种是基于网络距离。
对于分布在物理网络(如道路网)的事件集合,距离性矩阵保留了空间远近信息,在实际分析中会更为常用。本文考虑边集合无流量、等级等附属信息,使用节点间最短路径的长度作为网络距离。在计算过程中通过阈值进行限制,即当网络距离超过一定阈值就认为两者无关联。
2.2 事件属性融合事件的权重由事件的属性信息来表示,其基本假设为:如果一个事件的“影响”较大,那么周围的同类事件更有可能与其相关联。如在城市管理中,一处地方较大商家的明显占道行为很可能引起附近商家纷纷效仿。这种影响可以反应为空间上的交互性更强,因此,可将其与网络空间距离相融合,体现其对交互性的影响。值得注意的是,权重的选择是较为主观的过程,但相比完全忽略事件自身属性对时空过程的影响,可有效增强时空交互检验方法的表达能力。本文将事件的特性量化为事件的影响值,因此,权重矩阵 W Sn由原始矩阵 A Sn和事件权值加权融合后,对应具体检验方法进行转换而成。权值常有其物理含义,如占道事件的严重程度,其值跟专业知识密切相关。因此,在将距离矩阵和进行融合之前,需首先对权值进行标准化。设定权值标准化区间 R =[rmin,rmax],其反映了用户所期望的权值相对于空间距离影响的上下界限。定义线性映射函数fl,将加权值向量α映射到标准化后的权值向量αnew。设 α的取值范围为[a,b] ,fl函数表示为:

在得到标准化的加权向量 α new后,权重矩阵 W Sn中元素可以下式表示:
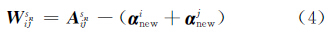
本文考虑矩阵元素都为正值,因此,W Snij最小值为0。在融合之后,需要根据阈值对 W Sn进行二值化,这个过程也可视为一个标准化过程。在具体应用中,加权值可代表一个事件点的轻重程度。
2.3 计算方法 2.3.1 数据预处理在计算空间权重之前,需要首先将事件集合 E插入到网络N 中。在城市管理系统中,事件的采集由城市网格化管理人员结合GPS定位信息进行标注,考虑到道路宽度、仪器精度等原因,标注的事件点位一般不会与道路网完全套合。因此,本文首先计算事件集合E中每个事件点投影到网络 N中距其垂直距离最近的边,形成投影点集Eproj,然后再将Eproj插入到网络N作为一类特殊的节点。网络中已有边在插入过程中会被插入的点打断形成新边。
2.3.2 网络空间权重矩阵构建本文论述的网络空间权重矩阵计算本质上是一个加入约束条件的最短路径问题。基本步骤如下:
1) 读取网络N,读取点集权值向量 α new;
2) 遍历事件点集Eproj,以点ei为起始点,基于Dijkstra算法计算其到网络其他节点的最短距离。保存计算结果为距离值向量 A i;
3) 依据所有最短距离向量(A1,A2,…,An)结果构建初始网络空间矩阵 A Sn;
4) 遍历矩阵元素,使用式(5)对矩阵进行逐元素计算,构建网络权重矩阵 W Sn;
5) 针对Baker’s修正Knox检验,对矩阵 W Sn进行逐元素与阈值h比较二值化。
2.3.3 指数值和显著性水平计算指数值依据式(2)对网络权重矩阵 W Sn和时间矩阵 A t进行点乘等基本运算求得。时空交互检验方法的蒙特卡洛随机模拟有两种常用方法:一种是固定空间将时间进行随机洗牌生成时间距离矩阵;另一种是固定时间将空间进行随机洗牌生成空间权重矩阵。两种随机洗牌方式的显著性水平结果无实质差别[2, 3, 10]。
本文选择固定时间属性进行模拟的方法。在进行n次模拟形成指数向量 I ,经验p值的计算方式可表示为[15]:

式中,r代表数组 I 中大于或等于原统计指数值的个数。计算得出的经验p值可代表时空交互作用的统计显著性。
3 实验分析 3.1 研究区域与数据本文使用2011-04-11至17日间发生于武汉市江汉区的1 535件占道经营数据进行实验分析。图 1显示了选取事件沿道路的分布情况。本文事件权值的选取直接基于原系统记录的文本描述信息根据占道经营的规模经过人工评分,再经分位映射函数标准化形成加权值。鉴于占道事件的相互影响一般为正相关且呈现在小范围的道路段内,本文将权重标准化范围定义为[0,30]。值得注意的是,这只是一个较为初步的经验选取过程,在后续实际应用过程中,权值及其标准化参数选取需要结合城市管理专家的经验以及过往数据的特征(如占道经营的性质是出店经营、杂物堆放,还是流动摊贩等)进行半自动化的选取。
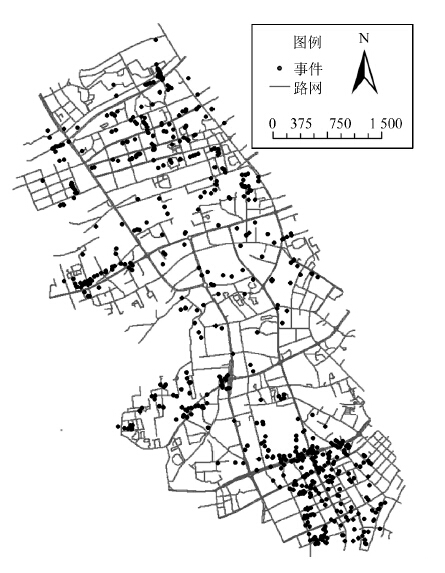 |
| 图 1 占道经营事件分布Fig. 1 Distribution of Road-stall Events |
Baker’s修正Knox检验衡量微观空间的事件聚集情况,其指数值反映了具有时空交互作用的事件对数,通过其与期望值的比较,可以衡量时空交互程度的强弱,而p值衡量了时空交互的统计显著性。本实验数据中将蒙特卡洛模拟次数均设定为999次,并分别取空间距离阈值为50 m、150 m、300 m,时间阈值为1 d、2 d、3 d、4 d、5 d,来对占道经营事件在不同时空尺度的聚集程度进行衡量。表 1为Baker’s修正Knox检验的分析结果。可见,占道经营事件在所选取的时空阈值内的时空交互作用都表现出明显的统计显著性(p=0.001)。表 1中加粗数字代表某一空间阈值内最大的指数值,可以看出,在同一空间阈值设定内,指数值随时间阈值增大而减小,证明事件在时间跨度上更趋向于聚集于1 d以内。
|
空间 阈值 /m | 时间 阈值 /d | 指数值 | 期望值 | 置信上限 | 置信下限 | p值 |
| 1 | 1 911.78 | -0.75 | 165.23 | -122.62 | 0.001 | |
| 2 | 1 563.96 | 0.84 | 169.66 | -163.69 | 0.001 | |
| 50 | 3 | 1 025.38 | 0.43 | 163.96 | -162.36 | 0.001 |
| 4 | 617.09 | -1.14 | 136.03 | -151.67 | 0.001 | |
| 5 | 318.73 | 1.51 | 88.52 | -95.00 | 0.001 | |
| 1 | 2 011.78 | 4.16 | 201.49 | -157.84 | 0.001 | |
| 2 | 1 535.52 | 1.00 | 224.93 | -173.72 | 0.001 | |
| 150 | 3 | 1 020.66 | 0.87 | 220.43 | -187.18 | 0.001 |
| 4 | 615.37 | -2.56 | 119.95 | -150.76 | 0.001 | |
| 5 | 342.16 | 0.00 | 106.52 | -109.28 | 0.001 | |
| 1 | 1 944.19 | -2.20 | 257.37 | -211.01 | 0.001 | |
| 2 | 1 353.45 | -1.36 | 269.33 | -282.35 | 0.001 | |
| 300 | 3 | 1 176.77 | 4.09 | 264.11 | -247.01 | 0.001 |
| 4 | 805.11 | -2.60 | 220.98 | -207.32 | 0.00 1 | |
| 5 | 424.08 | 2.00 | 135.29 | -145.45 | 0.001 |
本文通过构建道路网约束下的空间权重矩阵,并将事件属性信息通过权值形式融入矩阵的构建,将Baker’s修正Knox时空交互检验方法扩展到了融合语义信息的网络空间中。实验通过对武汉市城市管理事件分析,表明该方法可以为城市管理者提供一种灵活的聚集模式分析手段,以衡量沿网络分布事件的时空规律。通过事件权值属性融合,可以有限度地将城市管理的语义信息与分析方法结合,使得聚集趋势分析结果更加贴切的反映管理实践。未来将研究事件属性权值的合理设定及其设定对各类指数计算值的影响及影响程度,并进一步探讨局部的事件交互性强弱判别方法和各种时空交互性检验中的尺度因素对聚集程度的影响。
| [1] | Knox E G, Bartlett M S. The Detection of Space-Time Interactions[J].Journal of the Royal Statistical Society, Series C(Applied Statistics), 1964, 13(1):25-30 |
| [2] | Mantel N. The Detection of Disease Clustering and a Generalized Regression Approach[J].Cancer Research, 1967, 27(1/2):209-220 |
| [3] | Jacquez G M. A k Nearest Neighbour Test for Space-time Interaction[J].Statistics in Medicine, 1996, 15(18):1 935-1 949 |
| [4] | Schmertmann C, Assunc R, Potter J. Knox Meets Cox:Adapting Epidemiological Space-time Statistics to Demographic Studies[J].Demography, 2010, 47(3):629-650 |
| [5] | Wells W, Wu Ling, Ye Xinyue. Patterns of Near-Repeat Gun Assaults in Houston[J].Journal of Research in Crime and Delinquency, 2011, 49(2):186-212 |
| [6] | Yamada I, Thill J. Comparison of Planar and Network K-functions in Traffic Accident Analysis[J].Journal of Transport Geography, 2004, 12(2):149-158 |
| [7] | Lu Yongmei, Chen Xuwei. On the False Alarm of Planar K-function when Analyzing Urban Crime Distributed Along Streets[J].Social Science Research, 2007, 36(2):611-632 |
| [8] | Okabe A, Satoh T, Furuta T, et al. Generalized Network Voronoi Diagrams:Concepts, Computational Methods, and Applications[J].International Journal of Geographical Information Science, 2008, 22(9):965-994 |
| [9] | Yamada I, Thill J. Local Indicators of Network-Constrained Clusters in Spatial Patterns Represented by a Link Attribute[J].Annals of the Association of American Geographers, 2010, 100(2):269-285 |
| [10] | Eckley D C, Curtin K M. Evaluating the Spatiotemporal Clustering of Traffic Incidents[J].Computers, Environment and Urban Systems, 2013, 37(1):70-81 |
| [11] | Robertson C, Nelson T A, Macnab Y C, et al. Review of Methods for Space--Time Disease Surveillance[J].Spatial and Spatio-temporal Epidemiology, 2010, 1(2/3):105-116 |
| [12] | Baker R D. Identifying Space--Time Disease Clusters[J].Acta Tropica, 2004, 91(3):291-299 |
| [13] | Chen Jiangping, Zhang Lanlan, Yu Yuanjian, el al. Analysis on Epidemic of A/H1N1 Flu in Mainland China Based on Spatial Statistical Methods[J].Geomatics and Information Science of Wuhan University, 2011, 36(11):1 363-1 366(陈江平, 张兰兰, 余远剑, 等. 利用空间自相关的中国内陆甲型H1N1流感疫情分析[J].武汉大学学报\5信息科学版, 2011, 36(11):1 363-1 366) |
| [14] | Feng Xin, Du Shihong, Shu Hong. Influence of Spatial Weight Matrices on Spatial Autocorrelation:A Cased Study of HFRS in China[J].Geomatics and Information Science of Wuhan University, 2011, 36(12):1 410-1 413(冯昕, 杜世宏, 舒红. 空间权重矩阵对空间自相关的影响分析--以我国肾综合症出血热疾病为例[J].武汉大学学报\5信息科学版, 2011, 36(12):1 410-1 413) |
| [15] | North B V, Curtis D, Sham P C. A Note on the Calculation of Empirical P Values from Monte Carlo Procedures[J].American Journal of Human Genetics, 2003, 72(2):498 |
 2015, Vol. 40
2015, Vol. 40



