文章信息
- 曹波, 康玲, 谭德宝, 杨胜梅
- CAO Bo, KANG Ling, TAN Debao, YANG Shengmei
- 地震诱发堰塞湖下游淹没风险评估方法对比研究
- A Comparative Study of the Rapid Estimation of Downstream Flood Risk Induced by Dammed Lakes
- 武汉大学学报·信息科学版, 2015, 40(3): 333-340
- Geomatics and Information Science of Wuhan University, 2015, 40(3): 333-340
- http://dx.doi.org/10.13203/j.whugis20130164
-
文章历史
- 收稿日期:2013-05-22
2. 长江水利委员会长江科学院, 湖北 武汉, 430010
2. Changjiang River Scientific Research Institute, Changjiang Water Resources Commission, Wuhan 430010, China
我国是一个地震高发国家,“4·20雅安地震”和“5·12汶川地震”是近年来发生的规模较大的地震。地震本身能够引发多种次生灾害,山体滑坡形成的堰塞湖就是由地震诱发的次生灾害之一。地震引起的堰塞湖滑坡体具有渗透性强、稳定性差的特点。加上地震后普遍形成降水,堰塞湖的水位上涨迅速。坝体随时可能会由于漫顶溢流、管涌或者渗透形成瞬间溃决,其产生的洪水灾害破坏性远远大于一般山洪灾害,将给震后的下游人民的生命、财产带来难以估量的二次打击。因此,在堰塞湖安全处置、下游居民安全转移、科学抢险救灾等决策过程中,快速而准确地预测堰塞湖溃决造成的潜在淹没范围是问题的关键。
国内外关于堰塞湖下游淹没风险的研究正逐年增加[1, 2, 3, 4],特别是“5·12”汶川大地震时,当时的堰塞湖数量分布、险情威胁和救灾处置紧迫性均创造了多项历史之最。这就要求堰塞湖下游淹没风险评估应结合遥感、GIS、水文、水力学等多学科,充分利用灾区有限的数据资源开展快速而有效的应急响应。目前,对很多堰塞湖的研究仅局限于利用3S技术测定堰塞湖现有规模、依据水力学开展溃决模拟、下游洪水演进等单一专项上。水利专业计算结果缺乏空间展现能力,而遥感、GIS技术缺乏水力计算数据支持,很少有结合遥感影像、DEM、水文资料和GIS技术开展时效性强、响应时间短的堰塞湖溃决洪水淹没风险的研究,关于不同数据基础对不同计算方法精度影响和应用效果对比的研究更为少见。鉴于此,本研究分别采用水文流量演算法和二维水动力学模型法,对不同水位条件下溃坝洪水进行快速预测与模拟,在遥感技术和GIS平台的支持下,实现堰塞湖溃决后下游潜在淹没影响范围的模拟与展示,分析了两种方法各自的优势、局限性和对基础数据的依赖性,有针对性地提升了地震诱发堰塞湖突发事件应急处置能力。
1 研究区域与实验数据
本文选择2008-05-12四川省汶川里氏8.0级强烈地震震后形成的33个大型堰塞湖中规模最大的唐家山堰塞湖作为试验区。
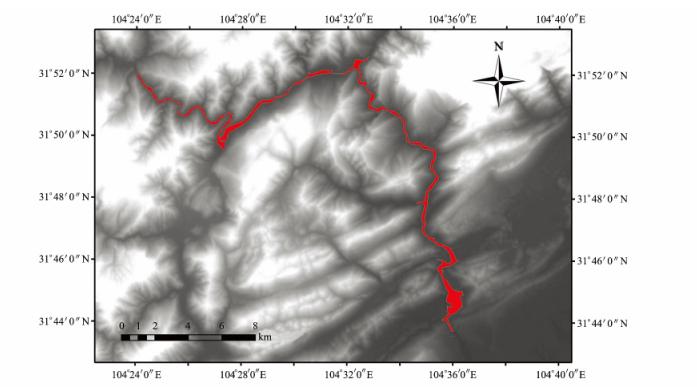
实验区数据收集了比例尺为1∶5万DEM和卫星遥感影像、航摄影像、卫星雷达影像、水文数据等。各类震后遥感影像(图 1)主要用于提取堰塞湖几何位置信息,并辅助评估下游淹没损失情况,DEM主要用于上游堰塞湖库容计算和下游洪水演进计算。DEM、水系和水文站点信息见图 1(d)。利用遥感影像解译技术可得,唐家山堰塞湖滑坡体位于涧河上游距北川县城约6 km处,顺河方向长约803 m,顺河垂直方向最大宽约611 m。依据DEM和GIS空间分析功能可得在进行施工处置前,该堰塞湖库容约2亿m3,并随着时间推移堰塞湖内的水位不断增高,时刻威胁着下 游地区。通过在DEM上预设不同高水位,可分别计算该水位下的堰塞湖容积从而获取水位-库容曲线,以此作为下游溃坝洪水的输入条件。在溃决水位和水量已知的情况下,本文将介绍 两种计算方法快速评估各种溃决水位下的下游淹没风险。

|
| 图 1 试验区数据 Fig. 1 Experiment Data |
水文学中常采用的流量演算法是由一维流动发展出的简化计算方法——马斯京根法[5]。与圣维南方程相比,该方法在数学形式上比较简单,稳定性高,适宜工程应用,并具有一定的物理意义。公式如下:
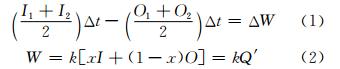
联立式(1)、式(2)可得马斯京根流量演算方程:
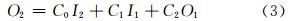
式中,
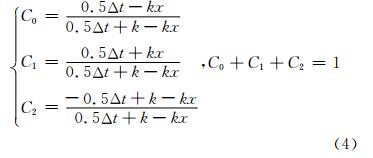
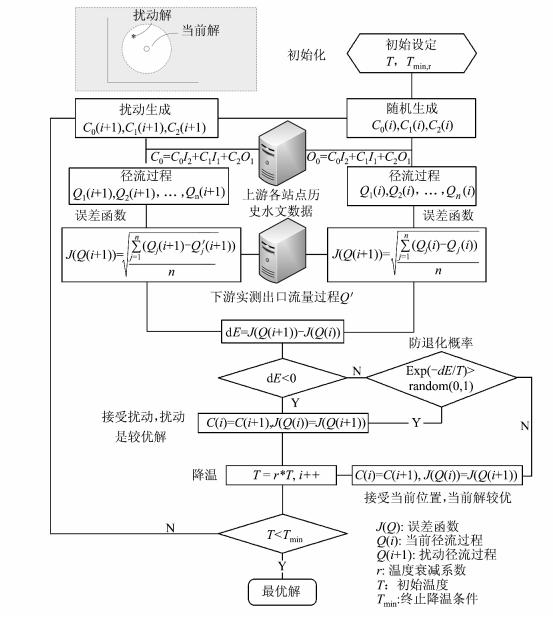
式中,I(input)和 O(output)分别为研究河段的上游入流和下游出流; W为该河段内的蓄水量;k 和X为参数,k 值是槽蓄曲线的坡度。式(3)是马斯京根法洪水演算公式的主体。传统求解C0、C1、C2参数的方法是试算法,该法精度不高且费时。在算法设计上也很难简单、准确地描述为机器可以很好理解和执行的准则。因此,本文采用模拟退火法(simulated annealing,SA)计算确定马斯京根参数,不必间接试算X值,可直接对马斯京根参数C0、C1、C2同时进行优化,极大地提高了计算速度和精度。程序随机生成在 (0,1)区间之内的C0、C1、C2则用1. 0、- C0、-C1代替。根据演算方程(3)带入水文历史数据进行训练,统计下游各时段末出流计算值O2与真实观测的流量之间的误差,以累积误差平方和作为误差评判函数J(Q(i))。然后给当前随机生成的马斯京根参数值C(i)一个扰动,生成一个邻居C(i+1),同理计算误差函数J(Q(i+1))。如果dE = J(C(i+1)) - J(C(i))≤ 0 ,则后次“扰动解”更接近最优解,令解空间C(i) = C(i+1),接受C(i+1)为向最优解移动路径上的i+1步的当前解。为了避免随机生成的参数在开始阶段即陷入局部最优,模拟退火算法思想中还以一定的防退化概率接受被认为不优的解,从而跳出局部最值。概率exp(-dE/T)按照实例解释就是计算时间还不长、两次解的差异很小时可依据较大的概率接受不优解,从而扩大有益的探索范围。直至多个回合误差不再下降,即为该河段满足多次洪水过程总体最优的C0、C1、C2值。图 2为马斯京根参数模拟退火详细流程。
|
| 图 2 模拟退火法求解河段马斯京根参数流程 Fig. 2 Muskingum Parameters Solution Based on Simulated Annealing |
参数训练采用2008-04~2009-10间大量的实测水文数据,利用模拟退火法率定唐家山堰塞湖至通口段、通口至香水段的演算方程系数,并以2008-06-10一次实测洪水过程对率定的演算方程系数进行精度检验,结果显示率定系数对洪峰模拟精度较高(表 1)。原因在于以误差平方和的形式构造评价函数时,算法对大数值、峰量级的流量误差控制能力较好。评价下游淹没风险的目标在于获取最大淹没影响范围,注重对洪峰模拟精度的要求,因此,采用误差平方和作为评价函数是切合实际应用需求的。
| 河段 | C0 | C1 | C2 | 评价函数收敛误差 | 洪峰值/(m3·s-1) | 演算值/(m3·s-1) | 相对误差/% |
| 唐家山至通口 | 0.172 2 | 0.161 5 | 0.666 3 | Jmin=4.583 2×106 | 5 720 | 5 517.713 | -3.54 |
| 通口至香水 | 0.519 7 | 0.281 9 | 0.198 4 | Jmin=5.000 0×106 | 5 520 | 5 484.85 | -0.64 |
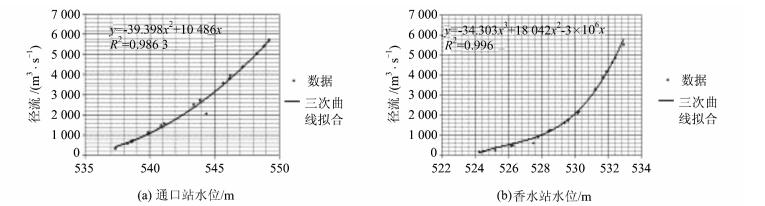
输入预设水位条件下堰塞湖发生溃决时所产生洪峰流量过程,即可利用表 1中的演算方程系数推求该次溃决洪水在唐家山堰塞湖至通口段、通口至香水段的流量过程。实测数据证明,通口、香水水文站所在断面是水位与流量有稳定关联的固定断面。因此,可依据图 3通口、香水站点的水位-流量关系曲线折算洪峰过境时通口、香水站的最高水位值。
|
| 图 3 通口与香水站的水位流量关系曲线 Fig. 3 Runoff versus Elevation Curve |
当得到洪峰过境时通口、香水站的最高水位值 h1、h2后,结合唐家山溃决水位h0,沿河道方向沿程均匀插值,得到一系列的河道水位值,再依据GIS的空间分析功能在DEM数据的支持下[6, 7, 8, 9]计算这些水位在该段河流的淹没范围,得到水文流量演算法所确定的堰塞湖溃决的潜在影响范围。
3 基于二维水动力模型法的下游潜在淹没影响范围研究
圣维南方程Saint-Venant equations由反映质量守恒定律的连续方程和反映动量守恒律的运动方程组成,是目前洪水演进计算的重要手段,其以Q、h为因变量的方程组形式为:
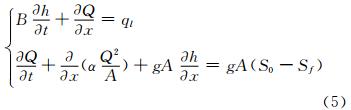
式中,Q、A、h分别为过水断面流量、面积与水深;t、x为时间变量和空间位移(水流平行方向);g、α为重力加速度和动量校正系数(一般情况α≈ 1.0);S0、Sf为底坡和摩阻比降;ql为旁侧入流量。 圣维南方程属于一阶双曲线性拟线性偏微分方程,很难用解析方法求解,一般通过数值计算获得近似解。常用的数值计算方法主要有有限差分法、特征法、有限单元法等[15]。
本文平面二维数学模型控制方程采用TVD-MacCormack有限体积法求解,空间离散采用控制体积法,时间离散采用预测-校正格式显式,溃坝激波的捕捉采用TVD技术,离散计算区域采用非规则四边形网格。稳定性分析采用CFL,又称Courant条件,可以通过选择适宜的时空步长防止数值扩散并节省计算时间:

式中,c为波速;Δt为计算时间步长;Δx为计算空间步长。
基于二维水动力方程的方式较之水文流量演算法,虽然计算任务繁重,所需的边界条件多,但是一旦计算完毕,就能清楚地了解计算河段各格网点的水位、流速、流向等全要素,再将全要素结果与遥感图像、DEM数据进行三维叠加显示,就可以逼真而细致地再现洪水淹没历程。
4 690 m溃坝洪水算例
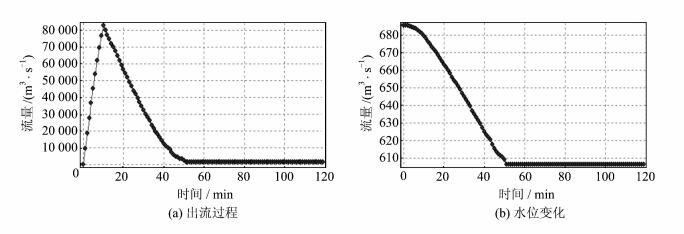
计算堰塞湖溃坝洪水流量过程的主要依据是堰流经验公式与水量平衡方程,同时还要根据溃前水位、溃底高程、溃口形状(三角、梯形等)与溃决模式(半溃、全溃)等条件得到与之对应的溃坝洪水流量过程[10, 11, 12, 13]。最大洪峰过境才会造成最大淹没影响,因此,可选择溃口形状为梯形及全溃模式为溃坝洪水的初始条件,当溃决水位为690 m时,依据堰流经验公式、水量平衡方程与唐家山堰塞湖水位库容曲线,得到如图 4所示的流量、水位变化曲线作为一维水文流量演算法和二维水动力模型法的输入条件,分别计算此种溃决方案下两种方法所得到的潜在影响淹没范围。
|
| 图 4 690 m水位时全溃模式下的流量、水位变化 Fig. 4 Process of Runoff,Elevation in Entirely Collapse Mode when Level is 690 m |
溃决前,堰塞湖形成后,河流正常输水功能被阻断,下游水量仅考虑地下水汇流到下游河流中形成的基本径流,该值是一个较小的稳定常数,可作为洪水演算溃决前的初始状态。根据堰塞湖形成后多天的水文观测数据可知,堰塞湖唐家山下游基流为3.2 m3/s,通口4 m3/s,香水2 m3/s。溃决中,考虑到淹没影响范围是最大洪峰过境时所形成的淹没影响,因此,洪峰值是最具代表意义 的特征值,根据图 4溃坝计算所得最大溃决下泄流量为Q0=82 000 m3/s。溃决后,溃坝流量在很短时间内由最大洪峰值衰减到上游天然来水量,形成一个洪水脉冲,取观测期间平均值76 m3/s。以马斯京根计算中河段传播的距离和传播时间量级相比较,溃坝时间太短,溃坝流量过程应简化处理,选取最具代表意义的特征值(洪峰值和天然来水过程)作为上游出流过程,可以不局限于溃坝洪 水短时的变化历程。依据以上水文流量特征数据,演算唐家山堰塞湖至香水段的流量变化过程。由于河段的连续性,上游唐家山至通口河段的出流值O1、O2实际上为下游通口至香水河段的入流值I′ 1、I′ 2,其具体流量过程演算表如表 2所示,时段间隔为1 h。
| 时段/h | I2/(m3·s-1) | I1/(m3·s-1) | O1 /I′1/(m3·s-1) | O2/I′2/(m3·s-1) | O′1/(m3·s-1) | O′2/(m3·s-1) |
| 1 | 82 000 | 3.2 | 4 | 14 123.6 | 2 | 7 341.5 |
| 2 | 76 | 82 000 | 14 123.6 | 22 666.7 | 7 341.5 | 17 217.9 |
| 3 | 76 | 76 | 22 666.7 | 15 128.2 | 17 217.9 | 17 667.8 |
| 4 | 76 | 76 | 15 128.2 | 10 105.3 | 17 667.8 | 13 021.6 |
| 5 | 76 | 76 | 10 105.3 | 6 758.5 | 13 021.6 | 8 944.6 |
| 6 | 76 | 76 | 6 758.5 | 4 528.5 | 8 944.6 | 6 033.3 |
| 7 | 76 | 76 | 4 528.5 | 3 042.7 | 6 033.3 | 4 054.9 |
| 8 | 76 | 76 | 3 042.7 | 2 052.7 | 4 054.9 | 2 729.0 |
| 9 | 76 | 76 | 2 052.7 | 1 393.1 | 2 729.0 | 1 844.1 |
利用图 3所示的通口与香水站的水位流量关系曲线,可以推出此种组合条件下通口与香水站洪峰(22 666.7 m3/s和17 667.8 m3/s)过境时的最大淹没水位分别是595.28 m和541.37 m。
最后对3个水位690 m、595.28 m、541.37 m基于河道距离进行插值,得到沿程水位值,再使用分段水位淹没法在DEM上得到水位H=690 m,最大溃决下泄流量Q0=82 000 m3/s全溃方式时,此种条件组合下的淹没影响范围。具体结果如图 5所示。
|
| 图 5 堰塞湖690 m溃决马斯京根预测淹没范围 Fig. 5 Inundated Area Acquired by Muskingum Method when Dam Breach Elevation is 690 m |
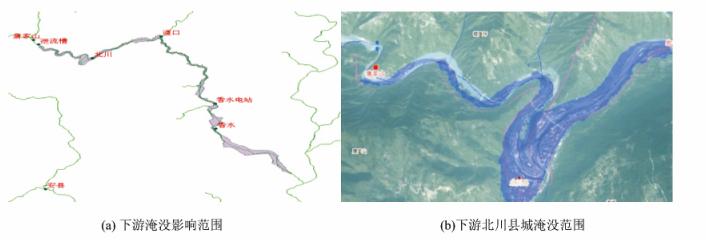
以690 m溃决时的流量、水位、库容曲线作为输入条件,结合水量平衡方程、地形和经验参数等边界条件,运用二维水动力学模型对堰塞湖溃塌后下游洪水演进进行模拟计算。计算结果主要包括洪水演进历程、洪水水深分布、洪水流速分布。这些计算结果按照时段将数据X、Y坐标及相应的水深及流速信息导出到文本文件,再将文本导入至ArcGIS系统并赋予与DEM、遥感影像一致的投影体系,将计算结果表现为点云和网格效果,通过GIS的插值功能形成面状体,最后与遥感影像或DEM数据套合,可查询均匀分布网格点各时段的水深、流量和流速等全要素信息,从而分析下游区域在相应溃决洪水作用下的危险程度。水力学计算结果是洪水演变过程,而淹没风险应该是沿程各处洪峰过境时的最大淹没范围,所以应将代表不同时段淹没范围的shpfile文件集合在ArcGIS中叠加求并集,以外包络线为准,即为下游淹没影响范围,主要计算结果如图 6所示。
|
| 图 6 堰塞湖690 m溃决条件下二维水动力模型计算结果 Fig. 6 Inundated Area Acquired by Hydrodynamics Method when Dam Breach Elevation is 690 m |
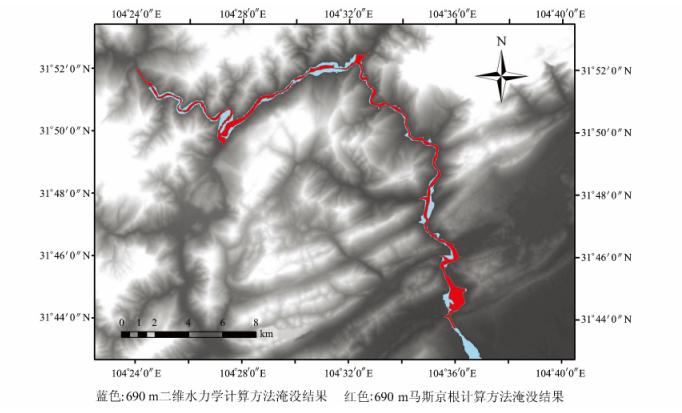
通过图 7中两种方法预测的淹没范围对比可知,两种计算结果均显示此种规模的溃坝洪水将淹没下游北川县城;在溃决条件一致的情况下,马斯京根预测淹没范围较水力学计算较小,并出现局部断流现象,具体原因分析如下。
|
| 图 7 唐家山至香水段两种预测方法淹没范围对比 Fig. 7 Comparative Inundated Area Based on Two Prediction Methods |
二维水力学计算依赖于DEM的精度,DEM正如水力学计算中的“水槽”。对目前已有DEM数据的分析可知,通口等河段因为测绘资料的原因缺少河道附近的地形,该区域只有590 m以上的地形,应该为“河底”的DEM区域比真实的河段高程(530 m左右)高出近60 m。造成二维水力学计算的基础被抬高、变宽,演算的淹没范围相应的会比真实情况偏大。
而马斯京根法计算的水位取决于水文历史数据,只是最后一步确定淹没范围时需要DEM,对DEM依赖性小。该方法计算水位低于该河段DEM时,就会出现断流的情况。
综上所述,二维水力学计算的精度取决于DEM模拟实际地形的逼真性。当地震区域不具备拥有水下地形的高精度DEM时,马斯京根的结果更符合实际情况。在时效性方面,水动力学模型方法耗时、计算量大,对于应用在注重时效性能的淹没范围快速评估研究上,该方法受到了一定的时间限制。对于拥有水文站历史数据但测绘资料精度有限的地区,马斯京根法更能适应在短时间内快速评估洪水危害和支持救灾决策。在计算精度和成 果内容表现力方面,当DEM精度有保证时,二维水力学计算物理意义严谨、要素齐全,成果更能准确而直观地描述洪水演进时空历程。
| [1] | Pan Shibing, Li Xiaotao. Using Remote Sensing Data to Monitor Dammed Lakes Caused by Wenchuan Earthquake[J].Journal of Geo-Information Science, 2009, 11(3):299-303(潘世兵, 李小涛. 四川汶川5·12地震滑坡堰塞湖遥感监测分析[J].地球信息科学学报, 2009, 11(3):299-303) |
| [2] | Fan Jianrong, Tian Bingwei. Investigation on Damming Object Induced by the Earthquake of Wenchuan on May 12 Based on Multi-platform Remote Sensing[J].Journal of Mountain Science, 2008, 26(3):257-262(范建容, 田兵伟. 基于多源遥感数据的5·12汶川地震诱发堰塞体信息提取[J].山地学报, 2008, 26(3):257-262) |
| [3] | Cui Peng, Zhu Yingyan, Han Yongshun, et al. The 12 May Wenchuan Earthquake-induced Landslide Lakes:Distribution and Preliminary Risk Evaluation[J].Landslides, 2009(6):209-223 |
| [4] | Hsu Y S, Hsu Y H. Impact of Earthquake-induced Dammed Lakes on Channel Evolution and Bed Mobility:Case Study of the Tsaoling Landslide Dammed Lake[J].Journal of Hydrology, 2009, 374:43-55 |
| [5] | Zhan Daojiang, Ye Shouze. Engineering Hydrology[M].3rd Edition. Beijing:China Water Power Press, 2000(詹道江, 叶守泽. 工程水文学(第三版)[M].北京:水利水电出版社, 2000) |
| [6] | Yang Shenghsueh, Pan Yiwen, Dong Jiajyun. A Systematic Approach for the Assessment of Flooding Hazard and Risk Associated with a Landslide Dam[J].Natural Hazards, 2013, 65:41-62 |
| [7] | Ehrlicha, D. et al. Identifying Damage Caused by the 2008 Wenchuan Earthquake from VHR Remote Sensing Data[J].International Journal of Digital Earth, 2009(2):309-326 |
| [8] | Zhai Yifeng. The Flood Disaster Assessment Model Based on GIS/RS[J].Yellow River, 2003, 25(3):6-7(翟宜峰. 基于GIS/RS的洪水灾害评估模型[J].人民黄河, 2003, 25(3):6-7) |
| [9] | Tolga G, Fan Xuanmei, Van Westen C. et al. Distribution Pattern of Earthquake-induced Landslides Triggered by the 12 May 2008 Wenchuan Earthquake[J].Geomorphology, 2011, 133:152-167 |
| [10] | Rahman M, Chaudhry M H. Simulation of Dam-break Flow with Grid Adaptation[J].Advances in Water Resources, 1998, 21(1):1-9 |
| [11] | Xue Yang, Xu Weilin, et al. Experimental Study of Dam-break Flow in Cascade Reservoirs with Steep Bottom Slope[J].Journal of Hydrodynamics, 2011, 23(4):491-497 |
| [12] | Long Wenfei, Zhang Xinhua. Study on the Prediction Method of Flood Due to Dam-break and Its Applications[J].Journal of Sichuan University, 2008, 40(1):21-26(隆文非, 张新华. 水库溃坝洪水预测方法研究及应用[J].四川大学学报, 2008, 40(1):21-26) |
| [13] | Peng M, Zhang L M. Analysis of Human Risks Due to Dam Break Floods(Part 2):Application to Tangjiashan Landslide Dam Failure[J].Natural Hazards, 2012, 64:1 899-1 923 |
 2015, Vol. 40
2015, Vol. 40


