文章信息
- 占伟伟, 王伟, 陈能成, 王超
- ZHAN Weiwei, WANG Wei, CHEN Nengcheng, WANG Chao
- 一种利用改进A*算法的无人机航迹规划
- Path Planning Strategies for UAV Based on Improved A* Algorithm
- 武汉大学学报·信息科学版, 2015, 40(3): 315-320
- Geomatics and Information Science of Wuhan University, 2015, 40(3): 315-320
- http://dx.doi.org/10.13203/j.whugis20130273
-
文章历史
- 收稿日期:2013-06-26
现代军事低空突防主要由无人机完成,为了提高无人机低空突防生存概率和作战效能,需要利用地形的遮蔽作用,在敌防御系统盲区内低空或超低空飞行。其中,关键问题是无人机的航迹规划。对于该问题的研究已有多年的历史,有很多研究成果。一些学者试图在人工智能等相关领域寻找智能优化算法,但它们解决大范围无人机路径搜索问题都有一些常见的弊病[1,2,3]。A*算法在二维图形搜索领域的成熟运用使得它解决该问题具有先天的优势[4],但目前成果存在以下问题:① 目标空间为小范围人造简单地形图,障碍物少且规则,未考虑雷达、恶劣天气等复杂威胁体[5,6,7]。② 一些学者使用平面区域划分(Voronoi图等)的方法[8,9,10],这类空间划分是基于一定高度的,因此本质上依然是在二维空间中进行路径规划。但山区地形实时截面运算的计算量太大,而且无人机基于一定高度上飞行的理论前提不成立。③ 不考虑无人机的机动性能约束,不是可飞航迹[5,6,7,8,9,10,11]。针对以上成果的不足,本文提出一种改进的A*算法,解决无人机在大范围复杂三维空间的实时路径规划问题。 1 方法 1.1 目标空间划分
A*算法是一种启发式搜索算法,需要一个由点和边组成的网络空间,在此目标空间中引入启发信息,由定义好的代价函数确定节点拓展的规则,最终得到两点之间的最优路径[4]。但基于DEM和DOM的三维环境本质上是一个连续状态的栅格空间,并不存在传统二维路径搜索中的路由网,从而无法利用路径搜索算法寻找最短路径中的节点和边,必须对其进行空间划分。
一些学者使用Voronoi图方法进行空间分割[9,10],它是一种基于障碍物特定高度截面的空间划分方法,而山区地形不同高度横截面差异很大,因此,在该路由网中生成的最优路径无太大参考价值。一些学者尝试使用规则三维网格的空间划分方法[7]。该方法的最大问题在于每个节点的可扩展方向在仅仅考虑邻域的情况下也有26个,要收敛到最优解会耗费大量的时间和内存资源,且随规划空间增大呈指数级增长。因此,提出了如图 1所示的2.5维网格模型,每个网格点包含经度、纬度、高程信息。此时每个节点的领域仅仅存在8个可扩展方向,算法计算效率要远大于3维网格划分方式。当然,网格大小必须在算法效率与搜索精度之间做出平衡。
 |
| 图 1 空间划分模型Fig. 1 Space Partition Model |
对于以上划分的目标网络空间,需要定义A*算法的代价函数对可拓展节点进行评估,从而挑选出最优路径中的节点-边列表。A*代价函数一般公式如下:
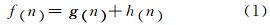
式中,n是待扩展节点;g n 是状态空间中从初始节点到节点n的实际代价;h n 是从节点n到目标节点的估计代价。 A*算法本身的性质决定了代价函数的表达式是影响搜索性能的主要因素。对于无人机低空航迹规划问题,Asseo 给出了对代价函数的参考公式[11]:
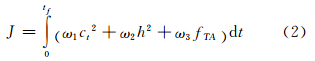
式中,ct为飞行器偏离指定航迹的距离;h为飞行高度;fTA为当前位置的威胁指标;ω1、ω2、ω3分别为相应的权重值。
针对本文的研究目标,该代价函数存在一定的问题。首先,ct是相对距离值,h是绝对海拔,它们并不处于同一个数量级的作用关系;fTA为到威胁点中心的距离,它对代价函数是正方向的作用关系,该值越小越好,ct、h则相反,因此很难分配对应项一个合理的权重值。其次,雷达并不是一个普通的威胁体,它对目标的威胁程度不能使用距离衡量,而是使用一个概率值来表达,它与其他两项的值将相差几个数量级,那么代价函数对ω1、ω2、ω3的值就不够敏感,很难指定一个合理的值使得代价函数处于一个对搜索结果有意义的状态。
为了解决以上问题,对代价函数进行了如下改进:
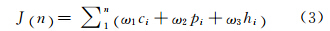
式中,ci为第i个节点与它前一个节点之间的地表距离,它是对航迹长度的直接惩罚,可以使得航迹以最快的速度向目标点靠近,而避免陷入局部最优和搜索死锁。pi是节点i与i-1之间的被探测概率。该项参数是为了提高无人机的存活率。hi为节点i与i-1之间的加权平均高度。
该代价函数的3项指标是同方向的作用关系,要求航迹长度越短、航迹高度越低、探测概率越小。但是它们并不在一个数量级上,因此,可以对各项惩罚指标进行归一化处理。采用0~1之间变换的关键是确定该指标变量的最大值和最小值。但节点之间的距离长短不一,地形也起伏不定,无法直接指定两点地表长度的最大值和最小值,但无论是真实的或人工设定的地形数据,最大和最小地形高度是已知的,或者也可以根据的地形数据计算出来,一旦确定了hmax和hmin,那么ci的最大最小值也可以确定了,如图 2所示。

式中,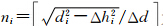 为节点i与i-1之间插值点的个数,di、Δhi、Δd是节点i与i-1之间的欧式距离、高度差和采样间隔。
为节点i与i-1之间插值点的个数,di、Δhi、Δd是节点i与i-1之间的欧式距离、高度差和采样间隔。
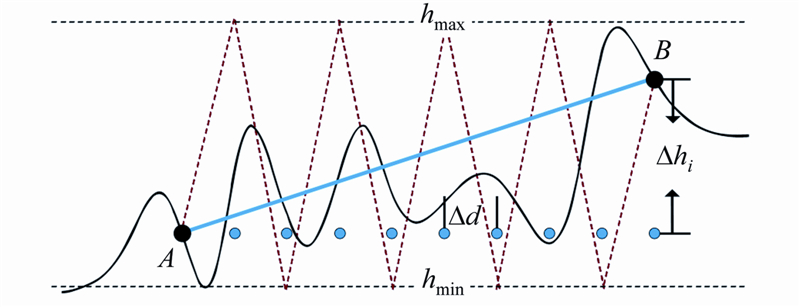 |
| 图 2 航段距离估算模型Fig. 2 Computing Model of Segment Distance |
pi是节点i与i-1之间的雷达探测概率,它必须考虑多个雷达的叠加影响,公式如下:
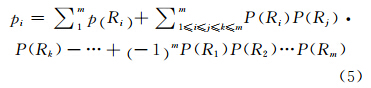
式中,p Rj 是节点i与i-1之间ni个插值点被第j个雷达探测的加权平均概率,每个点探测概率可由雷达方程反演得出。这三项指标最终归一化结果如式(6):
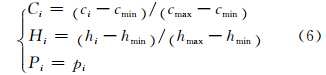
根据归一化结果得到新的代价函数如式(7),其中ω1+ω2+ω3=1。该代价函数将航线距离、高度、被探测距离归一化到同一个数量级,使得用户可以根据规划目标分配各自的权重,从而得到对应条件下的最优路径。
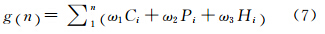
式(1)中h n 定义为节点n到目标点之间的地表距离,它可以促使节点n尽快向目标点靠近,从而使算法尽快收敛,则有:

式中,dn、dmax、dmin分别为节点n到目标点的地表距离、最大距离、最小距离,计算方法和式(4)类似,唯一的差别是为了提高h n 的计算效率,采样间隔ΔD往往比Δd大很多。 1.2.2 算法搜索流程
定义好目标空间和代价函数,即可开始航迹搜索。算法定义最小二叉堆open list和线性表closed list存放拓展节点,具体搜索流程如下:
1) 把起点S放入open list,记f=h,将closed list置为空表,读入起飞时间。
2) 重复下列过程,直至当前点与目标点距离小于阈值为止。若open list为空表,则提示用户在当前目标空间中该两点之间无满足初始条件的航路,航迹搜索失败。
3) 查找open list中未设置过的具有最小f值的节点为当前节点BN,并把它从open list中删除,且加入到closed list。
4) 若BN距离目标节点小于一定阈值,则成功求得目标解,终止循环。
5) 若BN不是目标节点,则对它进行拓展,得到相应的8领域节点。首先剔除已经在closed list中节点,然后剔除位于禁飞区和恶劣天气中的节点,将8领域节点中剩下的节点作为后继节点SUC。
6) 对每个SUC依次进行下列过程:
(a) 建立从SUC返回BN的指针。
(b) 计算SUC的代价,g(SUC)=g(BN)+h(BN,SUC)。
(c) 如果SUC∈OPEN,则将此节点标记为当前临时节点OLD,并把它添至BN的后继节点表中。
(d) 比较新路径代价。如果g(SUC)<g(OLD),则重新设置OLD的父辈节点为BN,记下较小代价g OLD ,并修正f OLD 值,否则停止扩展节点。
(e) 如果SUCOPEN,则判断其是否在closed list中,若SUC∈CLOSED,转向步骤(c),否则将它放入到open list中,并加入到BN的后裔表,然后转向步骤7)。
(f) 重新计算f值。
7) 循环以上步骤。 1.3 航线优化算法
§1.2.2搜索结果可能不满足无人机性能约束,包括最小步长、转弯半径、爬升率、安全高度等,需要对其进行一系列算法处理才能得到最终的可飞行航线。
最小步长、转弯半径是对航段在俯平面上的约束。前者要求航段长度大于一个特定值,后者则要求每一航段的长度需要同时满足无人机的前后两次转弯过程,因此,必须对航线数据进行数据压缩,本文采用FFP算法[12]对其进行数据压缩,它能够找出尽可能最长的直线趋势,从而避免无人机频繁的转弯。一条由航路点构成的折线依然是无法提供给无人机飞行的,有学者提出使用曲线平滑方法[13],如贝塞尔曲线、B样条等,但这与最小步长约束的相冲突,实际上,无人机一般通过旁切、飞越或向点等方式进行转弯,本文通过对应的数学描述对转弯保护区进行了建模和可视化。
升降率和安全高度是对航线在纵剖面上的约束。升降率是衡量无人机性能很重要的一个方面,飞机总是尽量保持自身的姿态,而不是频繁转弯或者升降。 如果两个航路点A、B高度不一样,飞机并不是直接从A点飞到B,而是依据A点的升降率,先完成高度的升降过程到达O点,再进行平飞到达航路点B,如图 3所示。安全高度是指为了保障飞机安全飞行所规定的离地表的最小额定距离,一些论文考虑了该限定值从而对航线进行约束[7],但它们仅在航线纵剖面上考虑该约束,而由于在飞行过程中,由于各种误差的影响,飞机的实际飞行路径在俯平面上与预定的航迹存 在偏离,因此算法应该在这整个偏离区范围内考虑安全高度,该偏离区即为航线的保护区,其对应的数学模型如图 4所示。保护区分主区和副区,其中主区提供全安全高度,副区的安全高度为从预定航迹向两侧逐渐减少直至为0,计算公式如下:
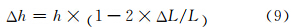
式中,h为安全高度(超障余度);ΔL为保护区内目标点到预定航迹的距离;L为保护区宽度。
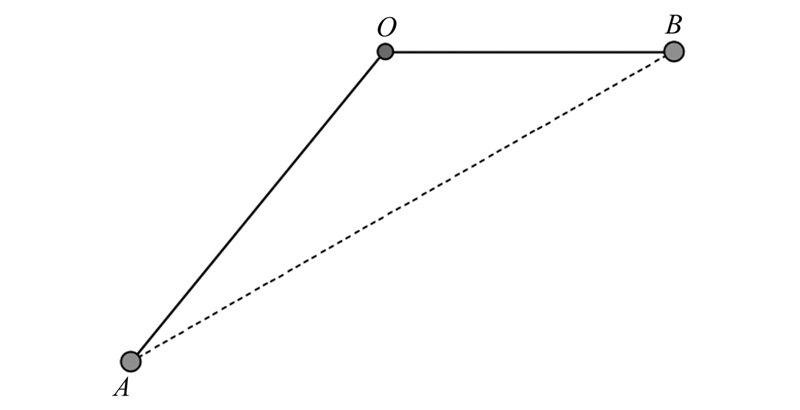 |
| 图 3 无人机爬升模型Fig. 3 UAV Climbing Model |
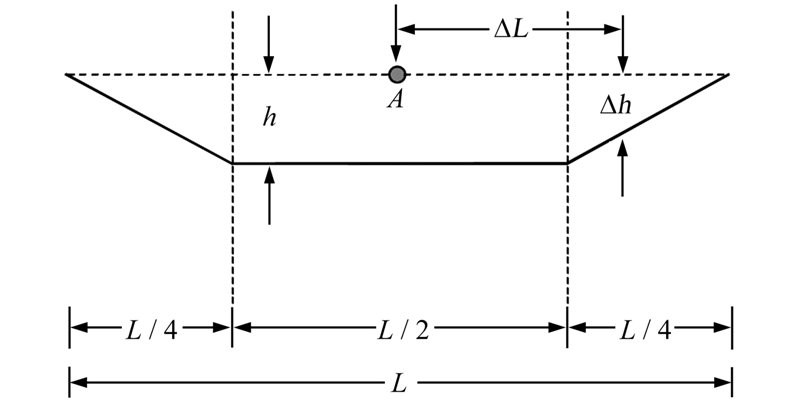 |
| 图 4 航线保护区模型Fig. 4 Route Safty Altitude Model |
根据以上数学模型,要使得在A、B航路点之间满足安全高度约束,可以求出保护区内的无人机高度与地形高度的最小有符号高度差ΔHmin,然后将航段AB的高度抬高 ΔHmin 即可,但考虑到在低空突防过程中,无人机的高度应尽可能小,因此可对算法稍作改进,计算步骤如下:
1) 将AB段分为AO、OB两段,其中O点是按照A点的升降率算出的平飞点。
2)求出OB段最小有符号高度差ΔH1。在OB之间按照进行插值(如等距插值),求出一系列插值点 Pi ,将Pi的横截面分为一个主区段和两个副区段,分别求出主区段和副区段的最小有符号高度差。
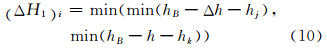
式中,(ΔH1)i是Pi横截面的最小有符号高度差;hB是OB的航段高度;Δh是安全高度;h是副区安全高度,计算原理如式(10)所示;hj是主区第j个插值点的地形高度;hk是副区第k个插值点的地形高度。遍历 Pi ,ΔH1 i的最小值即为ΔH1。
3) 求出AO段的最小有符号高度差ΔH2。现在AO之间进行插值,求得一系列插值点 Qi ,Qi的第i个横截面的最小有符号高度为:
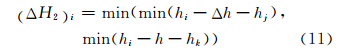
式中,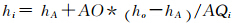 ,遍历{Qi},即可求得ΔH2。
,遍历{Qi},即可求得ΔH2。
4) 将O、B的高度调整到hB+ΔH1,将A的高度调整到hA+ΔH2,依据A点的升降率过A点作一条射线求得与OB的交点(可能在OB的延长线上),该交点为新的转折点O。 2 实验和分析 2.1 数据
本文实验中DEM和DOM数据分别是30 m精度的SRTM地形数据和30m精度的LANDSAT影像数据,实验区是西藏林芝到四川成都约200 km2的范围,该实验区大部分区域为山区,地形起伏变化明显,能够测试本文的搜索算法可行性和适用性。实验使用C#和SlimDX开发,已在三维GIS平台Gaea Explorer中顺利运行。实验硬件环境为CPU:Intel Core2 Duo E8200,内存:Kinston 1G,显卡:ATI Radeon HD 2600 XT。 搜索算法的初始参数为:速度300 km/h;坡度20°;升降率120 m\5s-1; 转弯方式为旁切;安全高度300 m;保护区宽度1海里。无人机的性能参数,目标航线和无人机性能是密切相关的。为了证明算法在不同距离上表现出的收敛性、稳定性及效率问题,设计了两组不同的坐标对照组,如表 1所示。
| 起点信息/(°) | 终点信息/(°) | 地表距离/km | 网格大小/(°) | ω1∶ω2∶ω3 |
|
93.832 779 29.127 954 | 94.372 746 29.319 841 | 59.783 | 0.1 | 1∶1∶1 |
| 93.562 434 29.168 065 | 105.587 785 30.119 375 | 1 236.916 |
图 5(a)~5(i)是在表2中第一个坐标组的一系列算法结果。其中,图 5(a)是初始搜索结果;图 5(b)是航线压缩结果;图 5(c)是转弯平滑结果;图 5(d)是爬升算法结果;图 5(e)是航线保护区生成结果;图 5(f)是考虑安全高度之后的航线保护区;图 5(g)是保护区横截面局部特写。从可视化结果可以看出,这一系列算法能有效地解决无人机低空航迹规划问题。图 5(h)是第一个坐标组考虑了雷达、禁飞区、恶劣天气等条件时的搜索结果,图 5(i)是其局部特写,图 5(j)、5(k)则是第二组坐标是否考虑这些条件的对照情形,图 5(l)是图 5(k)的局部特写。从局部细节可以看出,算法的确能够有效地利用地形的遮蔽作用,在敌防御系统盲区内低空或超低空飞行。
 |
| 图 5 算法结果可视化 Fig. 5 Visualization of Flyable Routes |
本文提出了一种改进的A*算法解决大范围三维战场环境的无人机航迹规划问题。提出了一种基于2.5维网格的三维空间划分方法,并且针对本文的最终目标,A*算法综合考虑了航线高度、被探测概率、航线长度等影响因子,同时满足UAV安全高度、升降率、转弯半径等性能约束,提出了一系列航线优化算法,得到了最终的可飞航线。实验结果证明,算法稳定、收敛性好、效率高,可满足大范围低空航迹规划要求,可运用于军事国防、应急救灾等相关领域之中。
但本文得到的航线是基于一定条件的最优航线,该处的条件不是指对结果的影响是可预知的那种类型,如无人机性能参数等,而是无法确定最优解的模糊情形。如通过一系列比较发现,在网格大小为0.1时,算法能够在搜索效率与搜索精度之间做出平衡,但这仅仅基于样例数据集的相对平衡,很难通过算法确定一个绝对最优的网格大小,因为该值是无法穷尽的。还比如ω1:ω2:ω3的取值对算法结果是有明显影响的,但很难确定一个比值来确保得到绝对最优的航线。除此之外,战场环境是一个动态变化的场景,如何改进算法以达到实时航迹规划也是一个巨大的挑战。
| [1] | Ge Xiaosan, Bian Fuling. On Algorithm for 3D Surface Route Optimization Based on Ant Colony Optimization[J].Geomatics and Information Science of Wuhan University, 2007, 32(4):366-368(葛小三, 边馥苓.蚁群算法求解三维表面路径方法的研究[J].武汉大学学报·信息科学版, 2007, 32(4):366-368) |
| [2] | Allaire F C J, Tarbouchi M. FPGA Implementation of Genetic Algorithm for UAV Real-Time Path Planning[J].J Intell Robot Syst, 2009, 54:495-510 |
| [3] | Garcia M A P, Montiel O. Path Planning for Autonomous Mobile Robot Navigation with Ant Colony Optimization and Fuzzy Cost Function Evaluation[J].Applied Soft Computing, 2009, 9:1 102-1 110 |
| [4] | Lu Feng. Shortest Path Algorithms:Taxonomy and Advance in Research[J].Acta Geodaetica et Cartographica Sinica, 2001, 30(3):269-275(陆峰.最短路径算法:分类体系与研究进展[J].测绘学报, 2001, 30(3):269-275) |
| [5] | Wang Hongwei, Ma Yong, Xie Yong. Mobile Robot Optimal Path Planning Based on Smoothing A* Algorithm[J].Journal of Tongji University(Natural Science), 2010, 38(11):1 647-1 650(王红卫, 马勇, 谢勇.基于平滑A*算法的移动机器人路径规划[J].同济大学学报·自然科学版, 2010, 38(11):1 647-1 650) |
| [6] | Hua Cao, Nathan E. Brener, S. Sitharama Iyengar.3D Large Grid Route Planner for the Autonomous Underwater Vehicles[J].International Journal of Intelligent Computing and Cybernetics, 2009, 2(3):455-476 |
| [7] | De Filippis L, Guglieri G, Quagliotti F.Path Planning Strategies for UAVS in 3D Environments[J].J Intell Robot Syst, 2012, 65:247-264 |
| [8] | Su Kang, Liu Jingnan, Yan Li.GIS-based Unmanned Air Vehicle Remote Planning[J].Geomatics and Information Science of Wuhan University, 2003, 28(2):188-192(苏康, 刘经南, 闫利.基于GIS的无人飞行器路径规划[J].武汉大学学报·信息科学版, 2003, 28(2):188-192) |
| [9] | Zhao Wenting, Peng Junyi.Voronoi Diagram-based Path Planning for UAVs[J].Journal of System Simulation, 2006, 18(2):159-162(赵文婷, 彭俊毅.基于Voronoi图的无人机航迹规划[J].系统仿真学报, 2006, 18(2):159-162) |
| [10] | Pehlivaoglu Y V. A New Vibrational Genetic Algorithm Enhanced with a Voronoi Diagram for Path Planning of Autonomous UAV[J].Aerospace Science and Technology, 2012, 16:47-55 |
| [11] | Asseo S J.Terrain Following Terrain Avoidance Path Optimization Using the Method of Steepest Descent[C]. Aerospace and Electronics Conference, NAECON 1988, Hawthorne, CA, 1988 |
| [12] | Chen Gang, Li Li.An Optimized Algorithm for Lossy Compression of Real-Time Data[C]. Intelligent Computing and IntelligentSystems(ICIS), Xiamen, 2010 |
| [13] | Yang Wangjin, Sukkarieh K.3D Smooth Path Planning for a UAV in Cluttered Natural Environments[C]. Intelligent Robots and Systems, IROS 2008, Nice, France, 2008 |
 2015, Vol. 40
2015, Vol. 40


