文章信息
- 张永军, 黄旭, 黄心蕙, 熊小东
- ZHANG Yongjun, HUANG Xu, HUANG Xinhui, XIONG Xiaodong
- 基于相交直线的相对定向方法
- Relative Orientation Based on Intersecting Lines
- 武汉大学学报·信息科学版, 2015, 40(3): 303-307
- Geomatics and Information Science of Wuhan University, 2015, 40(3): 303-307
- http://dx.doi.org/10.13203/j.whugis20130238
-
文章历史
- 收稿日期:2013-06-09
相对定向作为恢复核线几何和相机方位的重要手段,在摄影测量和计算机视觉领域,有着广泛的应用[1]。实际影像中存在丰富的线特征信息。线状特征在提供位置信息的同时,还可以提供线与线之间的相互位置信息。与点特征相比,线特征能够比较好地解决遮挡问题,能够解决纹理贫乏区域同名点稀少而无法定向的问题。鉴于上述优势,线特征已经引起摄影测量领域的关注[2,3,4,5]。
目前,基于线特征的相对定向已经有了一定的发展。Heuvel提出了基于平行四边形的相对定向[6]。Habib等利用线特征,以共面条件为约束,结合改进的广义Hough变换,进行相对定向计算[7]。Zielinski使用极坐标表示直线,在共面条件方程的基础上,加入线与线的夹角,两线相交于一点等约束条件[8]。文献[9,10]利用地面直线的水平与垂直关系代替共面条件,建立误差方程进行相对定向元素的解算。张祖勋提出了“广义点”的概念,将物理意义的点和数学意义的点以及不可见点统称为广义点,并将广义点数学模型带入共线条件方程,进行平差处理[11]。
以上方法均以线的几何特征作为约束,对条件方程进行改造。然而,这些方法依旧需要同名点的辅助,从而在计算时,引入较多的附加参数,造成未知数数目过多、计算量增大、解算困难以及对同名特征数目的需求增大等问题。同时,以上方法对直线特征的选取存在限制,线状地物需要满足一定的几何约束,造成方法的不通用性。
本文提出的基于相交直线的相对定向方法,能够完全不需要同名点的辅助,不引入任何附加参数,达到与传统相对定向方法近似的精度。由于相交是直线与直线之间最普通的特征,常见于房屋、道路、农田、工业零件等,因此,本文方法可应用于城市三维建模、工业摄影测量、LiDAR点云数据与航空影像配准[4,5]等方面。 1 数学模型
将空间直线的相交特征作为辅助信息,代替“共面条件方程”来进行相对定向解算,如图 1所示。
 |
| 图 1 同名相交直线示意图Fig. 1 Relative Orientation by Intersecting Lines |
图 1中,(l1,l 2;l′ 1,l ′ 2)表示同名相交直线对;S1、S2分别表示左右影像的摄影中心;L1、L2表示两条相交的物方直线。
分别采用3×1的齐次向量表示像方直线l1、l2、l′ 1、l′ 2。采用Plucker坐标表示物方直线L1、L2。令πi(i=1,2)表示摄影中心S1与直线li所构成的平面,π ′ i表示摄影中心S2与直线l′ i所构成的平面。π1,π ′ 1,π 2,π ′ 2可分别用一个4×1的齐次向量表示[12]:
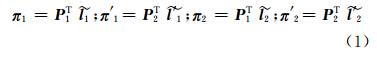
其中,l1、l′ 1 、l2 、l′ 2 表示内参数矩阵单位化下的像方直线坐标:

式中,像方直线l的坐标可以通过线段的端点进行计算:l=x1×x2,其中,符号×表示叉积;x1、x2分别表示线段端点的齐次坐标。K 表示内参数矩阵。P1、P2分别表示左右影像在内参数矩阵单位化下的摄像机矩阵。假定以左影像的像空间坐标系为坐标基准,左右影像的摄像机矩阵分别表示为:
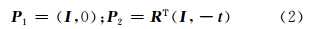
式中,R 是以相对定向角元素φ、ω、κ组成的旋转矩阵; t =(1,μ,ν)Τ表示相对定向线元素; I 表示3×3的单位矩阵;0 表示3×1的零向量。本文算法涉及的相对定向元素包括3个角元素φ、ω、κ和两个线元素μ、ν,与传统的连续法相对定向元素[1]一致。
空间直线L1、L2分别是平面π1、π′ 1之间和平面π2、π′ 2之间的交线。空间直线L1、L2 的Plucker坐标可以表示为:

式中,li12、li13、li14、li23、li42、li34(i=1,2)表示直线L1、L2 的Plucker坐标分量;vec()表示将4×4的Plucker矩阵向量化。
如果空间直线L1与L2相交,则存在如下函数关系[12]:
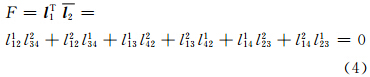
式中,符号-表示将向量的坐标分量倒序。
式(4)即为平差的基本数学模型。在给定相对定向元素初值的情况下,可将上式线性化,采用最小二乘平差理论,得到相对定向元素的精确解。式(4)对应的误差方程为:
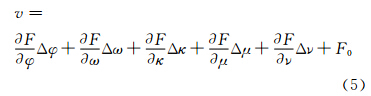
式中,Δφ、Δω、Δκ、Δμ、Δν分别为相对定向元素的改正数;F0是用相对定向元素的近似值求得的F值。式(4)中,各改正数的系数如下:
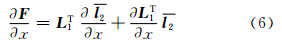
式中,x表示5个相对定向元素未知数。
根据式(2),有:
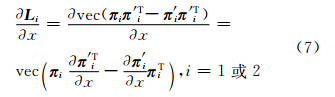
根据式(1),可得:
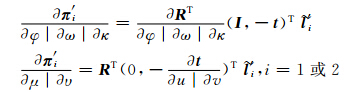
式中,符号 | 表示“或”的关系。 2 试验结果与分析
本文的试验采用3组影像数据:第一组影像数据为武汉市区某区域的航空影像;第二组影像数据为武汉大学遥感学院大楼的近景影像;第三组影像数据为武汉某河畔的倾斜影像。在前两组影像数据中,选取均匀分布的9对同名点,采用最小二乘匹配的方法精化;采用Canny算子,半自动地选取均匀分布的9对同名相交直线,采用最小二乘拟合的方法精化[13],以获得不同的定向结果。另外,在前两组影像上分别选取若干同名点作为检查点,以所有检查点到核线的平均距离作为检测定向精度的手段。在第3组影像数据中,提取均匀分布的9对同名相交直线,以直线的交点作为检查。在3组实验中,相对定向元素的初值均设为0,基线分量BX均设为1,因此,相对定向线元素μ、ν的单位为1。所有的参数解算结果和解算精度均保持6位小数。采用加粗的线代表提取的同名相交直线,圆圈的中心代表提取的同名点,如图 2~图 6所示。
 |
| 图 2 航空影像同名点、相交直线分布示意图Fig. 2 Distribution of Corresponding Points, Corresponding Lines in Arial Images |
在航空影像上,选取398对检查点。本次实验分别设计了3种方案,如表 1所示。 从表 1可以看出,针对航空影像,采用本文提出的算法,能够在不借助任何同名点辅助的情况下,取得较好的定向结果,其解算精度和迭代次数,与传统的连续法相对定向基本一致;当采用点、线联合平差的方案时,其解算结果更加稳定可靠,精度更高。实验结果表明,本文提出的算法能够很好地解决由于航空影像同名点不足而无法准确定向的缺陷。由于采用直线数据进行定向,与相交直线的端点无关,因此,能够在一定程度上解决遮挡问题,如图 3所示。
| 实验数据 | 参数解算结果 | 检查精度/像素 | 迭代次数 | ||||
| φ/rad | ω/rad | κ/rad | μ | ν | |||
| 9对同名点0对同名相交直线 | -0.020 618 | 0.060 651 | 0.015 821 | -0.017 788 | -0.002 909 | 0.353 758 | 5 |
| 0对同名点 9对同名相交直线 | -0.020 916 | 0.060 344 | 0.015 977 | -0.018 793 | -0.003 048 | 0.371 791 | 5 |
| 9对同名点9对同名相交直线 | -0.020 913 | 0.060 340 | 0.015 891 | -0.018 832 | -0.003 114 | 0.337 584 | 5 |
 |
| 图 3 航空影像物方相交直线提取局部放大图Fig. 3 Partial Enlargement of Extracted Intersection Lines in Arial Images |
由于传统基于点的相对定向方法无法避免遮挡问题,因此在遮挡较多的区域,采用本文提出的算法,获得的相对定向结果更加稳定可靠。 2.2 近景影像相对定向实验
在近景影像上,选取均匀分布的95对检查点。平差结果和解算精度如表 2所示。
| 实验数据 | 参数解算结果 | 检查精度/像素 | 迭代次数 | ||||
| φ/rad | ω/rad | κ/rad | μ | ν | |||
| 9对同名点 0对同名相交直线 | -0.045 930 | 0.004 007 | -0.014 373 | 0.068 255 | 0.049 169 | 0.610 620 | 5 |
| 0对同名点 9对同名相交直线 | -0.051 597 | 0.003 071 | -0.014 028 | 0.070 160 | 0.047 983 | 0.584 927 | 5 |
| 9对同名点 9对同名相交直线 | -0.046 191 | 0.004 387 | -0.014 563 | 0.066 804 | 0.048 703 | 0.524 309 | 6 |
与第一个实验类似,本文算法同样能够很好地适用于近景影像,无需同名点,即可取得较好的定向结果;当采用点、线联合平差时,能够提高定向结果的稳定性和精度。由于受近景影像几何畸变较大的影响,同名点、同名相交直线的提取和匹配精度会比较低,导致表 2中前两种方案的结果不是非常一致。但是根据检查点的检查结果来看,整体的定向元素解算是正确可靠的。另外,本文算法的计算结果完全能够满足后续的区域网平差等处理的需求。
 |
| 图 4 近景影像同名点、相交直线分布示意图Fig. 4 Distribution of Corresponding Points, Corresponding Lines in Close-range Images |
本文提出的算法,同样能够解决近景影像的遮挡问题,如图 5所示。
 |
| 图 5 近景影像相交直线提取局部放大图Fig. 5 Partial Enlargement of Extracted Intersection Lines in Close-range Images |
由于倾斜影像的几何畸变很大,拍摄区域多为河流和植被覆盖,纹理较为贫乏,加上相机视角问题,遮挡现象严重,所以很难提取出准确的同名点。但是影像中存在大量线信息,且线信息能够比较好地解决遮挡等问题。因此,可以将“线”取代“点”进行相对定向计算。参数解算结果和解算精度如表 3所示。
| 实验数据 | 参数解算结果 | 解算精度/像素 | 迭代次数 | ||||
| φ/rad | ω/rad | κ/rad | μ | ν | |||
| 9对同名相交直线 | -0.158 131 | 0.593 324 | 0.223 623 | -11.768 946 | 1.896 531 | 1.330 422 | 15 |
从表 3可以看出,本文提出的算法能够解决因同名点不足而无法定向的问题。但是由于影像几何畸变很大,提取线的精度较低,导致定向结果不是很理想,但是仍可满足后续区域网平差处理的需求。
 |
| 图 6 倾斜影像相交直线分布示意图Fig. 6 Distribution of Corresponding Lines in Oblique Images |
本文提出了一种基于相交直线的相对定向方法,以相交条件为约束,获得两张影像之间的相对定向元素。实验结果表明,本文方法能够取得与传统方法较为接近的精度,充分验证了本文算法的正确性和有效性;能够解决因为同名点缺乏而无法准确定向的问题。当采用点、线联合平差时,则能进一步提高相对定向的精度和稳定性。本文提出算法的局限在于:仅适用于相交直线特征较多的数码影像,且算法的精度与直线的提取精度密切相关。鉴于直线与直线之间还存在平行、垂直等关系,如何利用直线间的平行和垂直特征进行相对定向,是一个值得进一步研究的课题。
| [1] | Zhang Jianqing, Pan Li, Wang Shugen. Photogrammetry[M].Wuhan:Wuhan University press, 2003:23-27(张剑清, 潘励, 王树根. 摄影测量学[M].武汉:武汉大学出版社, 2003:23-27) |
| [2] | Ansar A, Daniilidis K. Linear Pose Estimation from Points or Lines[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 2003, 25(5):578-589 |
| [3] | Karjalainen M, Hyyppä J, Kuittinen R. Determination of Exterior Orientation Using Linear Features from Vector Maps[J].Photogrammetric Record, 2006, 116(21):329-341 |
| [4] | Habib A, Ghanma M, Morgan M, et al. Photogrammetric and LiDAR Data Registration Using Linear Features[J].Photogrammetric Engineering and Remote Sensing, 2005, 71(6):699-707 |
| [5] | Zhang Yongjun, Xiong Xiaodong, Shen Xiang. Automatic Registration of Urban Aerial Imagery with Airborne LiDAR Data[J].Journal of Remote Sensing, 2012, 16(3):587-595(张永军, 熊小东, 沈翔. 城区机载LiDAR数据与航空影像的自动配准[J].遥感学报, 2012, 16(3):587-595) |
| [6] | van den Heuvel F A. Exterior Orientation Using CoPlanar Parallel Lines[C]. Proceedings of the 10th Scandinavian Conference on Image Analysis, Lappeenranta, 1997 |
| [7] | Habib A, Asmamaw A, Kelley D, et al. Linear Features in Photogrammetry[R]. Department of Civil and Environmental Engineering and Geodetic Science, Ohio State University, 2000 |
| [8] | Zielinski H. Line Photogrammetry with Multiple Images[C]. ISPRS Archives, Washington D C, 1992 |
| [9] | Zhang Yongjun, Hu Binghua, Zhang Jianqing. Relative Orientation Based on Multiple Conjugate Features[J].Acta Geodaetica et Cartographica Sinica, 2011, 40(2):194-199(张永军, 胡丙华, 张剑清. 基于多种同名特征的相对定向方法研究[J].测绘学报, 2011, 40(2):194-199) |
| [10] | Zhang Yongjun, Hu Binghua, Zhang Jianqing. Relative Orientation Based on Multi-features[J].ISPRS Journal of Photogrammetry and Remote Sensing, 2011, 66(5):700-707 |
| [11] | Zhang Zuxun, Zhang Yongjun, Zhang Jianging, et al. Photogrammetric Modeling of Linear Features with Generalized Point Photogrammetry[J].Photogrammetric Engineering and Remote Sensing, 2008, 74(9):1 119-1 127 |
| [12] | Hartley R, Zisserman A. Multiple View Geometry in Computer Vision[M].Cambridge:Cambridge University, 2003 |
| [13] | Zhang Yongjun. 3D Reconstruction and Visual Inspectionof Industrial Sheet Metal Parts with Image Sequence[D].Wuhan:Wuhan University, 2002(张永军. 基于序列图像的工业钣金件三维重建与视觉检测[D].武汉:武汉大学, 2002) |
 2015, Vol. 40
2015, Vol. 40


