文章信息
- 方圣辉, 乐源, 梁琦
- FANG Shenghui, LE Yuan, Liang Qi
- 基于连续小波分析的混合植被叶绿素反演
- Retrieval of Chlorophyll Content Using Continuous Wavelet Analysis Across a Range of Vegetation Species
- 武汉大学学报·信息科学版, 2015, 40(3): 296-302
- Geomatics and Information Science of Wuhan University, 2015, 40(3): 296-302
- http://dx.doi.org/10.13203/j.whugis20130471
-
文章历史
- 收稿日期:2013-09-06
植被叶绿素是植被进行光合作用最重要的物质之一,准确估算植被的叶绿素含量对研究植被的生态效应具有重要意义。目前利用高光谱数据反演植被叶绿素主要有以下两种方法:① 经验与半经验模型方法[1];② 物理模型反演方法[2,3]。植被指数经验模型通过获取某些植被指数与叶绿素含量之间的经验关系,建立模型并反演叶绿素含量,其优点是模型计算简单易获取,但模型适应性有限。利用物理模型能取得较高的精度,但是需要了解部分生理生化参数,这些参数在实际应用时往往较难获取,同时物理模型反演时也会出现病态反演的问题。
小波分析是一种应用广泛的信号分析工具[4,5,6,7,8,9,10,11,12,13,14],目前已经应用在森林LAI制图、典型植被分类[10]等方面。在叶绿素反演方面,Blackburn利用小波分析进行了植被生化参数反演[6,7,8],宋开山等利用小波分析进行大豆叶绿素反演并取得了较高的精度[9]。Cheng等利用小波分析进行了病虫害探测[4]和叶片水分反演[7]并取得了较高的精度。连续小波变换将原始光谱信号在连续的波段上进行分解,分解后的系数与原始的光谱波段一一对应,在物理意义上相较离散小波变换更加清晰。但自然界中植被多是混合生长,针对混合植被的小波分析模型适应性有待进一步验证。本研究利用连续小波变换,分别在叶片与冠层两个尺度上,利用模拟数据与武汉地区实测数据进行了叶绿素反演实验,寻找适合用于不同尺度间混合植被叶绿素反演的小波尺度与波段,建立反演模型并与传统的植被指数经验模型进行了比较分析,同时进行了交叉验证。 1 方法和实验 1.1 实验数据集
实验数据集包含两个尺度上的4个数据集,分别是PROSPECT模拟数据集(PROSPECT)、PROSAIL模拟数据集(PROSAIL),武汉地区实测叶片数据集(WHL)与冠层数据集(WHC)。本文中通过生成一组数目为1 000的正态分布随机数来模拟混合植被的理化参数,作为物理模型的输入来生成模拟的植被光谱。部分主要输入参数的信息如表 1所示。表 1中无标准差的变量表示输入为固定值。
| 输入参数 | 均值 | 标准差 |
| PROSPECT | ||
| 叶绿素含量/(μg·cm-2) | 45 | 10 |
| 结构参数 | 1.5 | 0.4 |
| 水分含量/(g·cm-2) | 0.012 | 0.002 |
| 干物质含量/(g·cm-2) | 0.012 | 0.002 |
| SAIL | ||
| 叶面积指数 | 4 | 1 |
| 平均叶倾角/(°) | 45 | 10 |
| 太阳天顶角/(°) | 30 | - |
| 热点参数 | 0.2 | - |
| 土壤比率系数 | 0.3 | - |
| 观测方位角/(°) | 0 | - |
叶片实测数据采集于2012-04~2013-06之间,包含银杏、香樟、桂树、海桐、法国冬青、栾树、火棘、构树、晚樱、大叶黄杨、石楠、栀子在内的12种阔叶灌木或者小乔木,共143条光谱数据,其中石楠叶片光谱20条,栀子叶片光谱23条,其余叶片光谱均为10条。冠层实测数据采集于2013 年5~7月,包含以上12种植被共82条光谱数据,其中石楠冠层光谱10条,栀子冠层12条,其余均为6条。采集地点是武汉大学校区以及华中农业大学狮子山区试验田,测量植被长势均匀,所有光谱数据均采集于晴朗天气的10:00至15:00之间,叶绿素测定采用丙酮萃取法。冠层实测光谱数据采集时选择长势均匀的植被冠层,冠层叶绿素测量时选取上中下层的叶片各3片,测定叶绿素后计算均值作为冠层数据集叶片叶绿素含量,同时利用SunScan冠层分析仪测定植被叶面积指数(LAI),冠层叶绿素含量(CCC)通过式(1)计算[5],其中LCC为叶片叶绿素含量,LAI为叶面积指数。
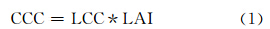
由于与叶绿素最相关的波段主要集中在红光与近红外波段,因此,本文选取400~1 000 nm波段之间的反射率来建立模型。4个数据集均被分为两组,其中60%的数据用来建立模型,余下40%数据用来验证模型精度。 1.2 植被指数经验模型
为了验证基于连续小波变换的叶绿素反演模型的精度,本文中同时建立起包括归一化差值植被指数(NDVI)、比值植被指数(SR)、比值植被指数705(SR705)、修正的叶绿素吸收率指数(MCARI)、MERIS陆地叶绿素指数(MTCI)、三角植被指数(TVI)、优化的土壤调节植被指数(OSAVI)等在内的7种常用于植被叶绿素反演的植被指数(表 2)与叶绿素含量的经验模型。但数据集中与叶绿素含量最相关的波段并不一定与植被指数定义中所使用的波段完全一致,因此对数据集中的光谱曲线,将所有波段两两组合,计算归一化差值植被指数并与叶绿素进行相关分析,得到与叶绿素最相关的归一化植被指数形式NDVIa_b并建立模型。其中a、b表示与叶绿素最相关的NDVI对应的两个波段。
| 指数 | 公式 |
| NDVI | (R800-R670)/(R800+R670) |
| SR | R800/R670 |
| SR705 | R750/R705 |
| MCARI | (R700-R670)-0.2(R700-R550)×R700/R670 |
| MTCI | (R750-R710)/(R710-R680) |
| TVI | 0.5120(R750-R550)-200(R670-R550) |
| OSAVI | (R800-R670)/(R800+R670+0.15) |
连续小波变换是一种广泛用于信号分析中的线性变换。它通过小波函数将信号分解为一系列的小波系数。通过对小波母函数进行尺度与平移变化,产生一系列小波函数。因此,本文中的尺度有以下两层含义: ① 数据集尺度,即叶片尺度与冠层尺度;② 小波变换的尺度即小波尺度。在给定的小波尺度上,通过平移小波函数与光谱信号相作用产生一个1×n的小波系数矩阵(其中n为波段),在m个尺度上进行小波变换就生成了n×m的连续小波变换系数矩阵,这个二维矩阵一维对应的是波长,另一维对应尺度,低尺度的小波系数反映了光谱信号的细节吸收特性,高尺度的小波系数对整个连续光谱曲线进行仿真。本文中连续小波变换在2,22,…,28的尺度上进行,这些小波尺度分别记为尺度1,尺度2,…,尺度8。大于28的尺度所表示的信息已经不具有意义[7]。使用Db4小波函数对4个数据集进行连续小波分析,将小波系数与叶绿素含量进行相关分析,提取最高的2%的相关系数平方(决定系数),对应的区域称为小波系数特征区域。 2 实验结果与分析 2.1 不同叶绿素含量下植被光谱
图 1是WHL数据集中不同叶绿素含量下的植被叶片光谱,可见叶绿素对植被光谱影响最大的区域在波长500~900 nm的区间内。随着叶绿素含量的升高,植被光谱550 nm附近的绿峰和800 nm附近的近红外平台的反射率值逐渐降低。相对于植被指数只能利用某些固定波段来进行建模,小波分析则可以捕捉到光谱在一定波长范围内曲线形状的变化[7,12,15]。
 |
| 图 1 不同叶绿素含量下叶片光谱 Fig. 1 Reflectance of Leaf for Different Chlorophyll Contents |
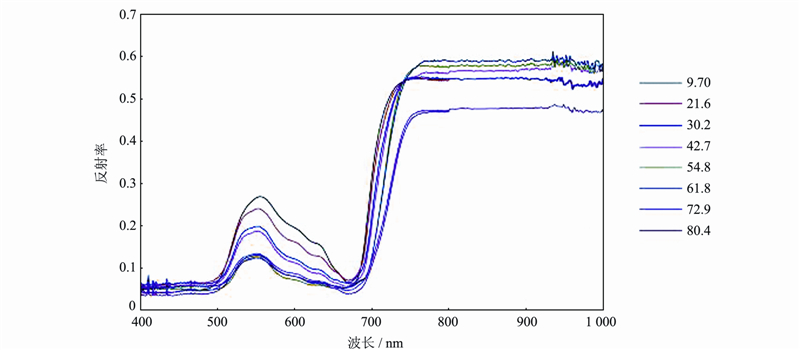
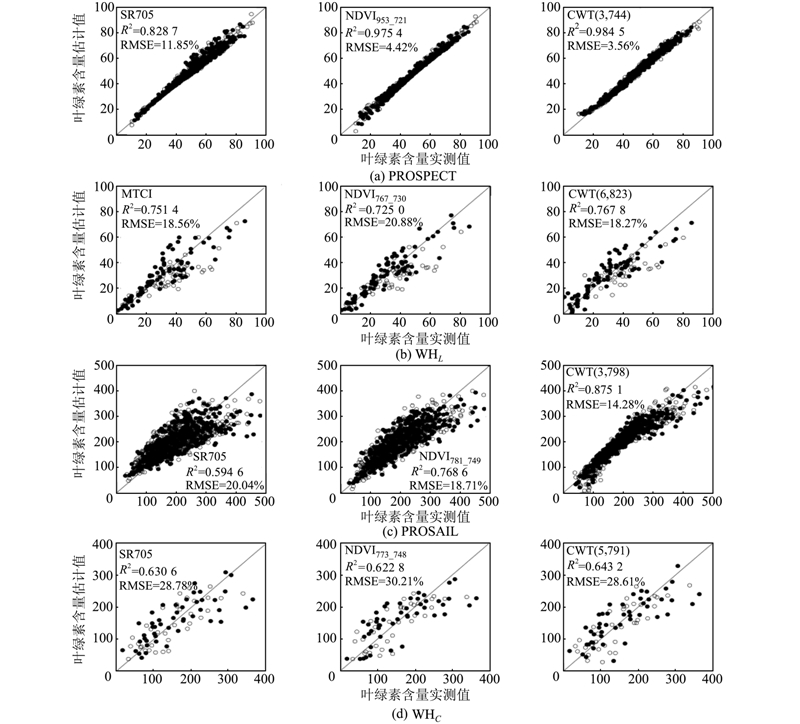
将两个叶片数据集建模数据进行8种植被指数的计算并进行线性回归,利用验证数据进行验证,得到的验证模型精度如表 4所示。在NDVI等植被指数中,SR705、MTCI、MCARI在两个数据集中的精度均高于其他植被指数,经过了相关性分析选取波段之后的NDVI指数能达到较高的精度,决定系数分别为0.975 4和0.725 0,但在两个数据集中最高相关波段有所不同。利用db4小波对两个建模数据集进行连续小波变换,将小波能量与叶绿素含量进行相关分析,得到决定系数图(图 2),获取前最高的2%的决定系数的小波特征区域并构建模型。表 3所示各数据集中 决定系数最高的前6个区域中最高决定系数所在位置。WHC数据集前2%的决定系数中,只有5个小波系数区域,因此,小波特征区域比其他数据集少一个。
| PROSPECT | WHL | PROSAIL | WHC | |
| NDVIa_b | (953,721) | (767,730) | (781,749) | (773,748) |
| CWT(A) | (3,744) | (6,823) | (3,798) | (5,791) |
| CWT(B) | (7,690) | (7,787) | (4,790) | (7,794) |
| CWT(C) | (4,753) | (6,753) | (1,782) | (6,821) |
| CWT(D) | (2,743) | (5,775) | (3,779) | (7,692) |
| CWT(E) | (1,743) | (5,737) | (2,789) | (6,759) |
| CWT(F) | (1,743) | (7,686) | (2,736) | - |
| LCC/CCC | PROSPECT | WHL | PROSAIL | WHC | ||||
| R2 | RMSE/% | R2 | RMSE/% | R2 | RMSE/% | R2 | RMSE/% | |
| NDVI | 0.311 5 | 23.75 | 0.173 2 | 23.82 | 0.535 1 | 21.30 | 0.400 7 | 32.90 |
| SR | 0.316 8 | 23.68 | 0.177 9 | 21.88 | 0.528 9 | 21.63 | 0.576 7 | 31.48 |
| SR705 | 0.828 7 | 11.85 | 0.763 9 | 15.81 | 0.594 6 | 20.04 | 0.630 6 | 28.78 |
| MCARI | 0.552 3 | 19.14 | 0.505 9 | 18.70 | 0.413 2 | 31.67 | 0.343 0 | 43.60 |
| MTCI | 0.760 0 | 14.01 | 0.751 4 | 18.56 | 0.563 4 | 20.72 | 0.598 3 | 28.96 |
| TVI | 0.079 0 | 27.45 | 0.008 1 | 47.18 | 0.099 3 | 45.68 | 0.003 6 | 62.85 |
| OSAVI | 0.074 8 | 27.51 | 0.197 4 | 38.77 | 0.279 1 | 40.94 | 0.229 5 | 44.38 |
| NDVIa_b | 0.975 4 | 4.42 | 0.725 0 | 20.88 | 0.768 6 | 18.71 | 0.622 8 | 30.21 |
| CWT(A) | 0.984 5 | 3.56 | 0.767 8 | 18.27 | 0.875 1 | 14.28 | 0.642 3 | 28.61 |
| CWT(B) | 0.978 2 | 4.23 | 0.757 1 | 18.25 | 0.845 8 | 15.65 | 0.555 1 | 30.78 |
| CWT(C) | 0.983 7 | 4.58 | 0.774 9 | 16.78 | 0.860 8 | 14.74 | 0.530 6 | 31.38 |
| CWT(D) | 0.962 6 | 6.94 | 0.656 5 | 22.42 | 0.857 7 | 14.75 | 0.543 7 | 30.95 |
| CWT(E) | 0.972 7 | 5.93 | 0.650 9 | 20.68 | 0.826 3 | 16.75 | 0.544 2 | 31.89 |
| CWT(F) | 0.977 9 | 5.34 | 0.509 2 | 23.61 | 0.809 3 | 17.34 | - | - |
由图表可知,PROSPECT模拟叶片数据集的最高相关区域集中在1~7尺度,650~950 nm之间(图 2(a)),各相关区域是离散的,而武汉叶片实测数据集的最高相关区域则集中在5~7尺度,650~950 nm之间(图 2(b))。两个数据集中最高相关小波系数模型的精度均高于最高相关NDVI模型精度。除开武汉实测叶片数据集中SR705模型与MTCI模型之外,小波系数模型精度均明显高于植被指数模型精度,略高于最高相关NDVI模型或与其持平。
 |
| 图 2 不同数据集叶绿素含量与小波系数的决定系数Fig. 2 Coefficients of Determination Between Wavelet Coefficients and LCC/CCC for Different Data Sets |
冠层尺度下小波系数特征区域的分布情况与叶片尺度相似。连续小波分析中,低尺度的小波能量反映了光谱信号的细节吸收特性,高尺度的小波能量对整个连续光谱曲线进行仿真,而实测数据由于各种环境因素的影响,测得的光谱数据细节信息已经不仅仅是植被所造成的,因此,低尺度的小波能量在反映植被叶绿的能力上有所下降。但高尺度的小波系数仍与叶绿素呈现良好的相关关系。
冠层尺度经验模型中,比较NDVI与SR的叶片尺度,精度均有明显提升,但TVI模型、OSAVI模型精度仍旧较低。叶片尺度中精度较高的MCARI在冠层尺度下精度有所下降。两个数据集中,最高的植被指数经验模型均是SR705,经过相关分析选取最高相关波段的NDVI指数在模拟数据中精度有明显的提升但在实测冠层数据集中,精度并没有明显的提升。
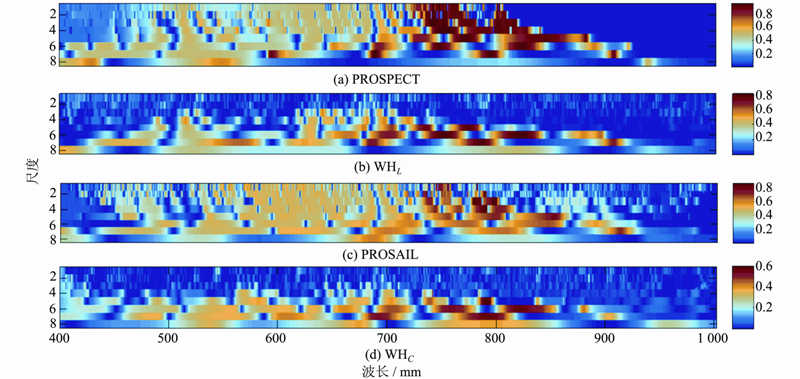
PROSAIL数据集中与叶绿素含量最高相关的小波系数在第3尺度,波长798 nm处,验证模型精度为R2=0.875 1,RMSE=14.28%,实测冠层数据集WHC中最高相关小波系数在第5尺度,波长791 nm处,验证模型精度为R2=0.642 3,RMSE=28.61%,且最高的决定系数均集中在第5尺度,波长791 nm附近,因此,其他区域的小波系数模型相比植被指数模型精度并没有明显的提升。
 |
| 图 3 不同数据集的叶绿素反演模型Fig. 3 R2 and RMSE Between Wavelet Coefficients and LCC/CCC for Different Data Sets |
图 4是各数据集的建模与验证模型,图中从左至右依次为精度最高的植被指数经验模型,最高相关NDVIa_b模型以及最高相关小波系数模型。实心圆表示建模数据,空心圆表示验证数据在4个数据集中,由于各种植被指数的构建都有其特定的反演对象与实用范围,导致各个数据集中植被指数表现不一,相对于植被指数只能利用某些固定波段来进行建模,小波分析则可以捕捉到光谱在一定波长范围内曲线形状的变化,因此基于连续小波分析的叶绿素反演精度均高于基于植被指数的经验模型精度。
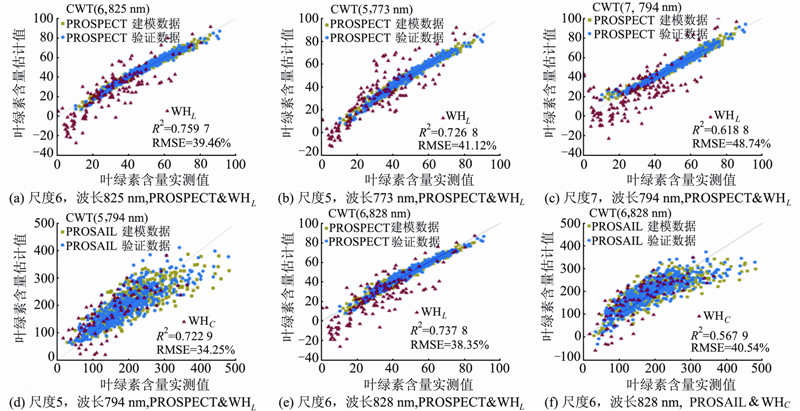 |
| 图 4 不同数据集之间的交叉验证Fig. 4 Cross Validation Between Different Data Sets |
为了验证基于最高相关小波系数模型在不同数据集之间的适应性,我们找到在不同数据集之间相同的小波系数特征区域。叶片尺度的相同区域有4个,分别是:第6尺度:747~751 nm,第5尺度:769~777 nm;第7尺度:793~794 nm;第6尺度:821~829 nm。冠层尺度的相同区域有1个,在第5尺度793~794 nm处。4个数据集之间在最高2%的决定系数中,没有相同的小波系数特征区域,将2%增大到5%时,出现一个相同的小波系数特征区域:第6尺度,828~831 nm。 在叶片尺度数据中,第6尺度,747~751 nm和821~829 nm中,PROSPECT建模数据集最高的决定系数在825 nm处,建立此处的小波系数同叶绿素含量之间的关系模型,并利用PROSPECT验证数据集,以及WHL整体数据集进行交叉验证,图 4(a)为验证结果。图 4(b)和图 4(c)分别为对第5尺度和第7尺度进行交叉验证结果。冠层尺度数据中选取小波系数则为第5尺度794 nm处,利用PROSAIL建模数据集建立模型(图 4(d))。图 4(e)和图 4(f)第6尺度,波长828 nm处两个尺度数据的交叉验证结果。注意到,当实测数据中叶绿素含量较低时(叶片尺度小于10,冠层尺度小于100),利用模拟数据建立的小波系数模型进行反演,会出现估计值为负值的现象,这是需要考虑的问题之一。实验结果表明,相同尺度下,通过模拟数据集建立的小波系数模型能够用于实测数据,适应性相比植被指数模型有一定的提升。 3 结 语
在叶绿素含量不相同时,植被叶片尺度光谱的变化是在一定波段范围内的全局变化,并且会受到诸如含水量、干物质含量、植被叶片结构等诸多因素的影响,冠层尺度下影响光谱的因素则更多,导致叶片尺度与冠层尺度之间小波特征区域有所不同。实测数据由于各种因素的影响,测得的光谱数据细节信息已经不仅仅是叶绿素所造成的,因此,低尺度的小波能量在反映植被叶绿素的能力上有所下降,这导致了模拟数据集与实测数据集小波特征区域的不同。相比传统的植被指数经验模型只能利用其中部分波段,连续小波分析通过模拟不同尺度的小波函数与植被光谱的相似性,能够捕捉到连续光谱范围内植被光谱的变化情况,因此,反演精度上相比较植被指数经验模型有明显的提高。相同尺度下,通过模拟数据集建立的小波系数模型能够用于实测数据,小波通过模拟一定波长范围内光谱反射率与小波函数的相似性,相比较植被指数利用了更多的信息,因此,适应性有一定的提升。
| [1] | Houborg R, Soegaard H, Boegh E. Combining Vegetation Index and Model Inversion Methods for the Extraction of Key Vegetation Biophysical Parameters Using Terra and Aqua MODIS Reflectance Data[J].Remote Sensing of Environment, 2007, 106(1):39-58 |
| [2] | Jacquemoud S, Bacour C, Poilve H, et al. Comparison of Four Radiative Transfer Models to Simulate Plant Canopies Reflectance:Direct and Inverse Mode[J].Remote Sensing of Environment, 2000, 74(3):471-481 |
| [3] | Jacquemoud S, Baret F, Andrieu B, et al. Extraction of Vegetation Biophysical Parameters by Inversion of the PROSPECT+SAIL Models on Sugar Beet Canopy Reflectance Data Application to TM and AVIRIS Sensors[J].Remote Sensing of Environment, 1995, 52(3):163-172 |
| [4] | Cheng T, Rivard B, S A Nchez-Azofeifa G A, et al. Continuous Wavelet Analysis for the Detection of Green Attack Damage due to Mountain Pine Beetle Infestation[J].Remote Sensing of Environment, 2010, 114(4):899-910 |
| [5] | Jesus D, Luis A, Gonzalo G, et al. Estimating Chlorophyll Content of Crops from Hyperspectral Data Using a Normalized Area over Reflectance Curve(NAOC)[J].International Journal of Applied Earth Observation and Geoinformation, 2010, (12) 165-174 |
| [6] | Blackburn G A, Ferwerda J G. Retrieval of Chlorophyll Concentration from Leaf Reflectance Spectra Using Wavelet Analysis[J].Remote Sensing of Environment, 2008, 112(4):1 614-1 632 |
| [7] | Cheng T, Rivard B, Sanchez-Azofeifa A. Spectroscopic Determination of Leaf Water Content Using Continuous Wavelet Analysis[J].Remote Sensing of Environment, 2011, 115(2):659-670 |
| [8] | Blackburn G A. Wavelet Decomposition of Hyperspectral Data:A Novel Approach to Quantifying Pigment Concentrations in Vegetation[J].International Journal of Remote Sensing, 2007, 28(12):2 831-2 855 |
| [9] | Song Kaishan, Zhang Bai, Wang Zongming, et al. Application of Wavelet Transformation in In-situ Measured Hyper Spectral Data for Soybean LAI Estimation[J].Chinese Agricultural Science Bulletin, 2006, 22(9):101-108(宋开山, 张柏, 王宗明, 等. 小波分析在大豆叶绿素含量高光谱反演中的应用[J].中国农学通报, 2006, 22(9):101-108) |
| [10] | Pu R, Gong P. Wavelet Transform Applied to EO-1 Hyperspectral Data for Forest LAI and Crown Closure Mapping[J].Remote Sensing of Environment, 2004, 91:212-224 |
| [11] | Zhang J K, Rivard B, Sánchez-Azofeifa A, et al. Intra and Inter-class Spectral Variability of Tropical Tree Species at La Selva, Costa Rica:Implications for Species Identification Using HYDICE Imagery[J].Remote Sensing of Environment, 2006, 105(2):129-141 |
| [12] | Song Shalei, Li Pingxiang, Gong Wei, et al. PLS Wavelength Selection by Hyperspectral Remote Sensing in Rice[J].Geomatics and Information Science of Wuhan University, 2010, 35(2):219-223(宋沙磊, 李平湘, 龚威, 等. 基于水稻高光谱遥感数据的PLS波长选择研究[J].武汉大学学报·信息科学版, 2010, 35(2):219-223) |
| [13] | Ni Ling, Zhang Jianqing, Yao Wei. SAR Image's Texture Analysis Based on Wavelet[J].Geomatics and Information Science of Wuhan University, 2004, 29(4):367-370(倪玲, 张剑清, 姚巍. 基于小波的SAR影像纹理分析[J].武汉大学学报·信息科学版, 2004, 29(4):367-370) |
| [14] | Luo Min, Zhu Xiaoming, Li Xiaohong, et al. Wavelet-Radial Descriptor Based Algorithm for Image Feature Extraction[J].Geomatics and Information Science of Wuhan University, 2008, 31(1):29-31(罗敏, 朱晓岷, 李小红, 等. 基于径向小波变换的图像特征提取算法[J].武汉大学学报·信息科学版, 2008, 31(1):29-31) |
| [15] | Gitelson A A, Gritz Y, Merzlyak M N. Relationships Between Leaf Chlorophyll Content and Spectral Reflectance and Algorithms for Non-destructive Chlorophyll Assessment in Higher Plant Leaves[J].Journal of Plant Physiology, 2003, 160(3):271-282 |
 2015, Vol. 40
2015, Vol. 40



