文章信息
- 朱丹, 董有福
- ZHU Dan, DONG Youfu
- 利用局部Moran's I指数进行DEM地形简化
- Terrain Simplification from Grid DEMs Based on Local Moran's I Index
- 武汉大学学报·信息科学版, 2015, 40(2): 280-284
- Geomatics and Information Science of Wuhan University, 2015, 40(2): 280-284
- http://dx.doi.org/10.13203/j.whugis20130085
-
文章历史
- 收稿日期:2013-04-28
地形简化算法是构建多尺度DEM数据库的重要方式[1]。国内外学者对DEM地形简化算法进行了大量的研究,Fowler与Little提出通过提取地形骨架线构建初始不规则三角网(triangulation irregular network,TIN),之后加入支持点迭代进行地形细节表达[2];Floriani等提出通过逐级三角形分割达到构建不同细节层次DEM的目的[3];Chen和Guevara提出通过计算目标高程点与周围8个点的平均高程值之差来评估其重要度,并选取重要程度高的点作为候选点重构DEM[4];黄培之提出将等高线几何分析与地形表面流水模拟分析相结合,通过分析地形特征要素的空间关系,从而决定地形特征要素的取舍[5];费立凡等通过全局性递归运算选取反映地形总体结构形态的地形特征点重构DEM,从而实现地形简化[6, 7, 8]。这些地形简化算法部分是根据局域高差变化对高程点进行取舍,执行效率高,但由于小范围内地形变化幅度较小,许多 位于地形骨架线上的特征点被忽略[9, 10];一些顾及全局地形结构特征的算法能够有效地保留地貌特征点,但地形要素提取或迭代处理对计算资源的要求相对较高[11, 12, 13]。本文在对DEM地形空间自相关性特征分析的基础上,提出了一种利用局部Moran’s I指数的DEM简化方案,通过提取一定数量的地貌特征点重构结果DEM,具有较好的DEM地形简化效果。 1 原理与方法 1.1 实验样区与数据
本文选定的实验区为陕北黄土高原韭园沟流域部分区域,总面积约4.3 km2,海拔830~1 200 m,为典型黄土丘陵沟壑地貌类型。基本实验数据采用国家测绘部门生产的1∶10 000(5 m分辨率)DEM。
1.2 基本原理
按照地理学第一定律,空间事物总在不同程度上相互联系与制约,而相近事物之间的影响通常大于较远事物的影响,这种现象被称为空间自相关。对于DEM数据而言,大部分栅格单元的高程值呈现出有序变化,即空间自相关程度较高,而少量栅格单元(如脊线点和沟谷点)的高程值表现出突变特征,即空间自相关程度较低。本文在求算DEM栅格单元空间自相关程度指数的基础上,选取一定数量的地貌特征点进行DEM地形简化。局部Moran’s I指数是度量某一栅格单元与相邻栅格单元空间自相关程度的常用指标,其计算公式如下:
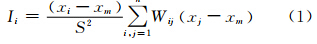

式中,xi、xj分别是栅格单元i、j的高程值;xm是所有i、j位置点高程值的均值;n是所有栅格单元的数目;Wij是研究范围内每一个栅格单元i与j之间的空间相邻权重矩阵。 Moran’s I指数的取值范围在-1 ~+1之间,越接近-1,代表单元间的差异越大或分布越不集中;越接近1,代表单元间的关系越密切,性质越相似(高值聚集或低值聚集);接近0,代表单元间无相关性。
1.3 过程与方法
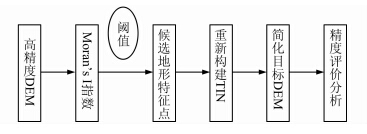
基于空间自相关特征的DEM地形简化方案如图 1所示。首先计算基准DEM栅格单元的局部Moran’s I指数,然后通过设置Moran’s I指数的适当阈值提取不同相关性程度的候选地形特征点,在此基础上,加入地形特征线构建约束不规则三角网(TIN),并进行插值处理,从而得到不同细节层次的简化结果DEM。最后从特征点空间分布、高程统计参数、地形结构特征和基本地形参数等方面与重要点法(very important points,VIP)作对比,进行地形简化效果综合分析。
|
| 图 1 基于局部Moran’s I指数的DEM地形简化方案 Fig. 1 Procedure of Terrain Simplification Based on DEMs Using Local Moran’s I Index |
在计算DEM栅格单元的局部Moran’s I指数时,采用3×3窗口,该窗口是计算局部Moran’s I指数常用的默认窗口大小,计算结果能够反映 DEM数据较大尺度上的空间自相关性;不同窗口大小反映在不同尺度上的地形空间自相关特征将在后续实验中进行深入探讨。
局部Moran’s I指数阈值设定是应用该方法进行地形简化的关键问题,其大小决定了简化结果DEM的细节层次。从图 2中可以看出,当阈值较大时,保留的候选地形特征点较多,能够较详细地反映地形的局部特征;当阈值减小时,仅保留地形骨架线上的特征点,低等级的沟谷和山脊逐渐被忽略。局部Moran’s I指数阈值设定方案与简化结果DEM间的相互关系将进行另外的实验分析,本文选取局部Moran’s I指数阈值为0.9对该地形简化方案的可行性进行验证,此时选定的地形特征点个数为25 711个,占实验区总栅格数的15%。

|
| 图 2 不同Moran’s I指数阈值的特征点分布和DEM简化效果 Fig. 2 DEMs Reconstructed with Different Moran’s I Index Values |
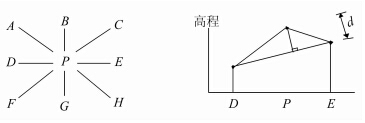
本文从特征点空间分布、高程统计参数和地形结构特征等方面,将VIP法作为对比算法,对利用局部Moran’s I指数重构DEM效果进行综合评价。VIP法是DEM地形简化中的常用方法,如图 3所示,VIP计算方法主要是根据局域范围内的地形起伏状况来选点,即针对规则网格DEM中的每一个点位,计算其高程值与周围8个点的平均高程值之差,根据这个差值评估目标高程点在地表描述中的重要度,若差值较大,意味该中心点与邻域点的高程值变化较大,选取该点作为候选地形特征点用于重构DEM。
|
| 图 3 VIP计算方法示意图 Fig. 3 Calculate Schema of VIP Method |
为了保证地形简化效果的可比性,VIP法用 于重构结果DEM的候选地形特征点数目与局部Moran’s I指数法相同。图 4是两种地形简化方法得到的DEM地形简化效果图。从图 4中可以看出,局部Moran’s I指数法保留的大部分特征点集中分布在山脊线和山谷线上;而VIP法保留的特征点主要位于局域高差较大的沟谷以及坡面上,而对重构地形相对重要的一部分山脊点和沟谷点,由于其局域地形变化幅度不大而被忽略。从重构结果DEM的效果图上看,Moran’s I法能够较好地保持地形骨架特征,而VIP法在坡面和低等级沟谷细节表达上效果较好。

|
| 图 4 候选地形特征点空间分布和重构DEM晕渲图 Fig. 4 Spatial Distribution of the Terrain Feature Points and the Hillshades of Reconstructed DEMs |
中误差(root mean square error,RMSE)是目前通用的DEM质量评价标准。该方法是在实验样区布设一些检验点,记录检验点的实际高程,然后在重构DEM的相应位置上,将DEM模型表示的高程值与实际高程相比较,得到各个检验点的误差。假设检验点的实际高程为zk(k=1,2,…,n),在重构DEM上对应这些点的高程为Zk,n为布设检验点的个数,则重构DEM的中误差为:
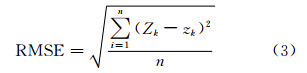
表 1是应用两种地形简化方法得到的结果DEM高程统计参数。与初始DEM相比,高程均值差都在-1 m左右,相对而言,VIP法的高程均值差更小,对于高程中误差RMSE,两种方法统计的结果都较小,并且VIP法相对更低。从以上分析来看,应用这两种方法进行DEM地形简化都能较好地保持高程统计特征,同时Moran’s I法的高程统计参数要略大于VIP法,反映了后者在地形细节表达方面的效果相对更好。
| 统计参数 | 高程均值差 | 高程中误差 | ||
| Moran’s I法 | VIP法 | Moran’s I法 | VIP法 | |
| 统计值 | -1.71 | -0.71 | 2.38 | 1.54 |
等高线回放是DEM生产过程中进行质量检验的主要方法之一,即对重构DEM反生等高线与原始等高线进行对比分析,能够有效地判断DEM对地形结构表达的效果。因此,简化DEM的地形结构线应尽可能与原始DEM中的地形结构线保持一致。
图 5是应用两种方法得到的简化DEM反生等高线与原等高线套合的部分结果。从图 5中可以看出,重构DEM的等高线与原始等高线在整体结构方面保持了较高的一致性,但是在局部细节方面,Moran’s I法等高线回放结果没有VIP法好。如图 5中部分等高线所示,基于Moran’s I法的DEM反生等高线的弯曲程度差异较大,尤其在坡面细节的表现上比较明显,基于VIP法的DEM反生等高线保持了相对较好的匹配效果,与原等高线几乎重合。

|
| 图 5 重构DEM等高线回放对比(灰色为原始 DEM反生等高线;黑色为重构DEM反生等高线) Fig. 5 Overlapped Maps of the Contours Extracted from Reconstructed DEMs |
汇水线和分水线也能够有效地反映地形结构特征。图 6是简化DEM与原始DEM生成的汇水线和分水线套合结果。从图 6中可以看出,与原始DEM生成的汇水线相对照,应用局部Moran’s I指数得到的简化DEM,其汇水线的整体轮廓和结构与原始DEM的汇水线在位置上的套合程度较好,这是因为局部Moran’s I指数保留 了主要汇水线上的地形特征点,但简化DEM忽 略了局部结构细节,导致汇水线出现部分裁弯取直的效果;VIP法简化DEM提取的汇水线位置和形态差异较大,尤其是地形平坦开阔的沟谷区存在一定的错位现象,主要是由于地形起伏变化小,重要栅格单元高程值被舍弃,水流方向发生变化,最终导致水系结构出现差异。另外,分水线和上述汇水线具有类似的特征,局部Moran’s I指数简化DEM提取的分水线与原始分水线在位置和轮廓上的吻合程度较高;通过VIP法简化得到的分水线的形态差别较大,尤其是地形平坦的山谷沟壑处。

|
| 图 6 简化DEM的汇水线和分水线套合对比(白色为原始DEM汇水线和分水线; 黑色为简化DEM汇水线和分水线) Fig. 6 Overlapped Maps of the Channels and Ridges Extracted from Reconstructed DEMs |
本文提出的DEM地形简化是基于空间自相关特征的局域地形简化算法,具有原理明确,易于实现,执行效率高,重构DEM高程精度较优等特点,相对于VIP局域地形简化算法,它能够有效地保留反映地形整体结构的地貌特征点;但是简化结果DEM坡面部分的地形变化点易被忽略,在地形细节方面的刻画与描述效果不及VIP法。
局部Moran’s I指数阈值的设定是保证地形简化达到预期效果的关键,并且只能在一定的阈值范围内才能较好地保留地形骨架特征,因此阈值设定标准有待进一步研究。此外,目前只对黄土丘陵沟壑区进行了实验,并取得了较好的效果,应用该方法对不同地貌类型区DEM进行地形简化的阈值参数、重构效果及适用性还需进行实验分析。
| [1] | Zhou Qiming, Liu Xuejun. Digital Terrain Analysis[M]. Beijing:Science Press, 2006(周启鸣, 刘学军.数字地形分析[M].北京:科学出版社, 2006) |
| [2] | Fowler R J, Little J J. Automated Extraction of Irregular Network Digital Terrain Models[J]. Computer & Graphics, 1979, 13:199-207 |
| [3] | Floriani D, Falcidieno B, Nagy G, et al. A Hierarchical Structure for Surface Approximation[J]. Computer & Graphics, 1984, 8:183-193 |
| [4] | Chen Z T, Guevara J A. Systematic Selection of Very Important Points (VIP) from Digital Terrain Model for Constructing Triangular Irregular Networks[C]. Auto-Carto 8, Baltimore, USA, 1987 |
| [5] | Huang Peizhi. A New Method for Extracting Terrain Feature Lines from Digitized Terrain Data[J]. Geomatics and Information Science of Wuhan University, 2001, 26(3):247-252(黄培之.提取山脊线和山谷线的一种新方法[J].武汉大学学报·信息科学版, 2001, 26(3):247-252) |
| [6] | Fei Lifan, He Jin, Ma Chenyan, et al. Three-dimensional Douglas-Peucker Algorithm and the Study of Its Application to Automated Generalization of DEM[J]. Acta Geodatica et Cartographica Sinica, 2006, 35(3):278-284(费立凡, 何津, 马晨燕, 等.3维Douglas-Peucker算法及其在DEM自动综合中的应用研究[J].测绘学报, 2006, 35(3):278-284) |
| [7] | He Jin, Fei Lifan. Further Study on Three Dimensional Douglas-Peucker Algorithm and Its Application to Generalization of DEM[J]. Geomatics and Information Science of Wuhan University, 2008, 33(2):160-163(何津, 费立凡.再论三维Douglas-Peucker算法及其在DEM综合中的应用[J].武汉大学学报·信息科学版, 2008, 33(2):160-163) |
| [8] | Fei Lifan, He Jin. A Three-dimensional Douglas-Peucher Algorithm and Its Application to Automated Generalization of DEMs[J]. International Journal of Geographical Information Science, 2009, 23(6):703-718 |
| [9] | Cai Xianhua, Zheng Tiandong. A Study of DEM Data Compression and Its Algorithm[J].Bulletin of Surveying and Mapping, 2003(12):16-18(蔡先华, 郑天栋.数字高程模型数据压缩及算法研究[J].测绘通报, 2003(12):16-18) |
| [10] | Wu Fan, Zhu Guorui. Multi-scale Representation and Automatic Generalization of Relief Based on Wavelet Analysis[J]. Geomatics and Information Science of Wuhan University, 2001, 26(2):170-176(吴凡, 祝国瑞.基于小波分析的地貌多尺度表达与自动综合[J].武汉大学学报·信息科学版, 2001, 26(2):170-176) |
| [11] | Wu Yong, Tang Guoan, Yang Xin. Accuracy Analysis of Multi-scale DEM Derived by Wavelet[J]. Bulletin of Surveying and Mapping, 2007(4):38-41(吴勇, 汤国安, 杨昕.小波派生多尺度DEM的精度分析[J].测绘通报, 2007(4):38-41) |
| [12] | Liu Xuejun, Wang Yanfang, Jin Bei. A Upscaling Method of Digital Elevation Model with Point Spread Function[J]. Geomatics and Information Science of Wuhan University, 2009, 34(12):1 458-1 462)刘学军, 王彦芳, 晋蓓.利用点扩散函数进行DEM尺度转换[J].武汉大学学报·信息科学版, 2009, 34(12):1 458-1 462) |
| [13] | Tang Guoan, Zhao Mudan, Cao Han. An Investigation of the Spatial Structure of DEM Errors[J]. Journal of Northwest University (Natural Science Edition), 2000, 30(4):349-352(汤国安, 赵牡丹, 曹菡.DEM地形描述误差空间结构分析[J].西北大学学报(自然科学版), 2000, 30(4):349-352) |
 2015, Vol. 40
2015, Vol. 40



