文章信息
- 孙雅庚, 郭庆胜, 刘远刚, 吕秀琴, 郑春燕
- SUN Yageng, GUO Qingsheng, LIU Yuangang, LV Xiuqin, ZHENG Chunyan
- 顾及格式塔原则的建筑物群移位实数编码遗传算法
- Coded Genetic Algorithm Considering Gestalt Principles to Building Displacement
- 武汉大学学报·信息科学版, 2015, 40(2): 269-273
- Geomatics and Information Science of Wuhan University, 2015, 40(2): 269-273
- http://dx.doi.org/10.13203/j.whugis20130540
-
文章历史
- 收稿日期:2013-09-28
2. 武汉大学测绘遥感信息工程国家重点实验室, 湖北 武汉 430079;
3. 嘉应学院地理科学与旅游学院, 广东 梅州 514015
2. State Key Laboratory of Information Engineering in Surveyings, Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China;
3. School of Geograhical Science and Tourism, Jiaying University, Meizhou 514015, China
地图综合中,由于比例尺的减小或一些综合算子的运用,会产生各种空间冲突,如地图目标间的相互压盖,或者目标间距离太小而无法辨认。空间冲突的解决是地图综合研究的重要内容。解决空间冲突问题的综合算子有多种,如移位、收缩、合并、删除等,其中移位算子是解决空间冲突最重要也是最复杂的算子。针对街区建筑物移位的空间冲突处理,已有很多专家学者进行了相关研究[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]。
移位在本文被视为一个连续性问题,即建筑物在一个给定的移位空间范围内,通过连续的移动获得较好的位置来解决冲突。因此,移位问题的复杂度就取决于地图上建筑物的个数多少和移位范围的大小。从大量的可能解中找到最优解,这是一个启发式搜索的问题。
遗传算法(genetic algorithm,GA)作为一种随机搜索算法,具有很强的全局搜索能力,特别适合求出问题的最优解,用GA求解移位问题是可行的[6],而GA的实数编码方式更适合于连续性问题的求解。但GA本身存在易早熟和陷入局部最优的缺点,为了克服这个不足之处,本文提出了一个对交叉概率和变异概率进行自适应调整的方法,并将其引入实数GA中进行建筑物移位问题的求解。同时,在求解可能解(或候选解)的过程中,充分利用地图感受规律(格式塔原则),试图提高求解的收敛速度,并得到了很好的移位效果。
1 格式塔原则
本文只讨论地图综合过程中因街道符号的加宽所产生的空间冲突问题。通过移位解决空间冲突,移位后的建筑物群还应符合地图感受规律和视觉认识规律,这主要体现在3个方面:①建筑物与街道的邻近相接关系。若有冲突,移位后的建筑物应该继续保持与街道相接的关系,这是一种“完形”性原则;②建筑物群排列方式的保持在移位前后要保持一致,这是一种“连续”性原则。如图 1中,图 1(a)表示正确的移位结果,移位后既保持了“完形”原则,又保持了“连续”性原则;图 1(b)无视建筑物群的直线排列分布特征来移位,破坏了“连续”性原则;图 1(c)则考虑了建筑物群的直线排列特征,但移位后没有满足原图中建筑物与街道的相接,不符合“完形”原则。关于如何识别直线排列建筑物群的空间分布模式不在本文的研究范围之内,文献[11]给出了这方面的研究;③地图目标的位置,当移位量小于视觉可识别距离时,可以认为该目标在视觉上没有移位,但在计算模型中仍然属于“有移位”,这属于地图感受规律,也需要在移位模型中考虑。
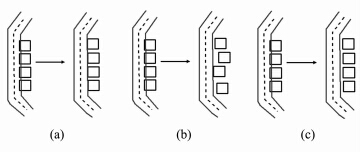
|
| 图 1 呈直线排列建筑物群的3种移位结果 Fig. 1 Three Displacement Results of Alignment Buildings Cluster |
在本文所研究的移位模型中,结合GA的计算特点,分别在评价函数和算法过程中考虑上面所提到的规律。 2 自适应实数编码遗传算法 2.1 编码
编码是将各分区中建筑物的每种移位方案转换成GA种群中的一个个体,每个个体对应一种移位方案。依上文所述,本文采用实数编码构造GA种群的个体。建筑物移位用X方向移位量和Y方向移位量两个变量表示其移位信息,两个变量构成一个基因,所有建筑物的基因组合在一起构成一个个体。
为了计算和限制每个建筑物可能的移位量,需要明确建筑物的移位范围。首先逐个计算出与街道冲突的建筑物为了解决冲突分别 在X和Y方向的移位量;然后从中找出在X和Y方向上的最小值和最大值,分别为ΔXmin、ΔYmin、ΔXmax、ΔYmax,它们就是分区内建筑物的移位范围。
2.2 交叉、变异
交叉算子采用了中间重组方法[12],在第s代,两个个体中进行交叉操作的分量分别为Cvs和Cws,交叉后的对应分量分别为Cvs+1和Cws+1,如式(1)和式(2)所示,其中α1、α2是取值为[0,1]之间的均匀随机分布数。
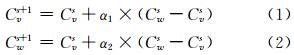
交叉之后的个体以很小的概率发生变异。移位量变异公式见式(3)和式(4):
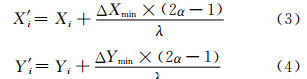
其中,X′ i、 Y′ i为变异后的移位量;Xi、Yi为变异前的移位量;α为[0,1]之间的均匀分布随机数;λ为变异步长,其值越小,变量变异的幅度越大。
2.3 适应度函数
本文中目标函数为:
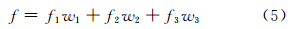
其中,f1表示建筑物与建筑物之间的冲突个数,本文采用缓冲区探测冲突,当两个建筑物之间的最小距离小于给定的最小距离阈值时,则冲突存在;f2表示建筑物与街道之间的冲突个数,当建筑物与街道有重叠或建筑物与街道间的最小距离小于给定阈值时,冲突存在;f3表示所有建筑物的移位量之和,f3越大,移位后的地图相比原地图而言破坏越大,具体计算公式见式(6),本文计算的距离为实际距离(m);w1、w2和w3分别表示相应的权重值。

可见,目标函数是求最小值,而GA中是适应度值越大,个体越容易被选中,所以需要从目标函数中变换出适应度函数。因此,选取目标函数的倒数F=1/f作为适应度函数。
移位要在解决空间冲突的前提下尽量保持地理对象间的空间关系和空间分布规律不变。为了使算法对冲突更敏感,权重w1和w2的值大于w3,利用w3来约束移位量大小,使建筑物群在冲突已解决的情况下尽量少移位。由于主要冲突来自道路符号扩宽后与建筑物之间的冲突,因此建筑物与道路的冲突被认为比建筑物之间的冲突更重要,要优先解决,三个权重关系为w2>w1>w3。其中,w3的设置对移位效果的影响也很大,若w3的值太小,较大的移位量虽然能解决冲突,但对原始地物间的空间关系破坏较大,同时,过大的移位量使与街道相接的建筑物移位后离开街道的距离太大,为了保持格式塔中的“完形”原则,当建筑物被力拉回与街道相接时,破坏了建筑物与其周围其他建筑物间的空间关系;若w3的值过大,虽然移位量变小,但又不利于空间冲突的解决。 2.4 自适应概率调整
GA存在过早收敛的缺点。GA中的交叉概率和变异概率对系统性能有重要影响。交叉概率越高,可以越快收敛到最优解区域,但过高的概率也可能导致过早收敛;交叉概率小,搜索过程缓慢。变异率太大,会使遗传算法变为随机搜索,引起算法不稳定;变异率太小,又不易产生新的个体[12]。本文引入一个度量种群多样性的指标[13],根据种群多样性的变化来自适应地调整交叉概率和变异概率,从一定程度上克服了过早收敛的问题。
通过适应度空间分布的方差来度量种群多样性变化。 设第t代种群个体为x1、x2、 …、xn,适应度值分别为f1、 f2、…、 fn,第t代所有个体的平均适应度值为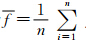 ,第t代个体的适应度方差为
,第t代个体的适应度方差为 ,并记下从第1代到第t代为止最大的适应度方差Dmax,定义指标Δ=Dt/Dmax表示种群的多样性特征。
Δ的取值在[0,1]之间。Δ越大,种群的多样性越高,种群个体间差异较大,比较分散;Δ越小,种群的多样性越低,说明种群各个体趋于一致或者趋于局部最优,过早收敛的可能性较大。因此,算法的交叉概率Pc和变异概率Pm可以随Δ值的变化而变化。当Δ较小时,增大Pc、Pm;当Δ较大时,减小Pc、Pm。
,并记下从第1代到第t代为止最大的适应度方差Dmax,定义指标Δ=Dt/Dmax表示种群的多样性特征。
Δ的取值在[0,1]之间。Δ越大,种群的多样性越高,种群个体间差异较大,比较分散;Δ越小,种群的多样性越低,说明种群各个体趋于一致或者趋于局部最优,过早收敛的可能性较大。因此,算法的交叉概率Pc和变异概率Pm可以随Δ值的变化而变化。当Δ较小时,增大Pc、Pm;当Δ较大时,减小Pc、Pm。

其中,k1、k2为常数,分别为人为设定的Pc、Pm的最大值。Pc和Pm在进化中根据种群多样性指标Δ的变化情况线性地调整自身大小:当种群适应度趋于一致、多样性降低时,增加Pc、Pm,使GA能探索新的区域,克服过早收敛;当种群适应度分散时,降低Pc、Pm,从而在局部区域调整解,增加算法的收敛速度。
但是,当Pc、Pm增大时,最优个体被破坏的概率也变大,为了保护每一代生成的最优解,本文采用精英选择的方式,将每一代中的最优解直接复制到下一代。
2.5 运算效率的提高
GA的运行时间主要与种群大小、迭代次数和适应度函数有关。种群越大,迭代次数越多,适应度函数计算越耗时,GA运行时间就越长。但较大的种群数目可以同时处理更多的解,容易找到全局最优解。因此,为了提高GA的运行效率,可以通过提高适应度函数的计算效率来实现。
对每个多边形及其重心编号,做重心的Voronoi图,则每个多边形在Voronoi图中有一个与其编号对应的区域,如图 2所示。然后判断其他Voronoi多边形或者街道是否与其相接或相交来判断是否相邻,若相邻,则加入其邻近关系中。由于邻近关系是对称关系,即A与B相邻,则B也与A相邻,在存储和查找中都会造成浪费,因此,在寻找邻近关系时,只从区域编码大于自身的区域中查找。计算适应度时,只需判断每个多边形的相邻多边形或街道即可,而无需遍历所有要素,节省算法的运行时间。
|
| 图 2 街区内多边形重心的Voronoi图 Fig. 2 Voronoi Graph of Buildings |
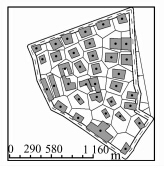
实验图如图 3所示(目标比例尺为1∶5万),图上最小可分辨距离为0.2 mm,交叉率最大值k1设为0.9,变异率最大值k2设为0.1。权重w1、w2、w3的值分别为20 000、30 000、1,权重如此设计是为了充分考虑空间冲突的处理。
实验前,先找出在原始图中与街道相接的建筑物,如图 3、图 4、图 5中灰色填充的建筑物,用GA移位后还需将其拉回,使其仍然保持与街道相接;然后识别出规则排列的建筑物群,在每次迭代中,随机选取其中一个建筑物的移位量作为整组建筑物群的移位量,即将规则排列建筑物群视为一个整体移位。

|
| 图 3 移位前的实验图 Fig. 3 Experimental Map Before Displacement Treatment |

|
| 图 4 估计格式塔原则 的实数GA移位 Fig. 4 Displacement of Real-coded GA Considering Gestalt Principles |

|
| 图 5 普通GA移位 Fig. 5 Displacement of Standard GA |
图 4与图 5是在相同参数条件下顾及格式塔原则的自适应实数编码GA和普通二进制编码GA两种算法移位后的实验图。 可以看到,两种算法对建筑物群的整体空间关系都保持得较好,但在空间冲突的解决方面,自适应实数GA表现更好,移位后已无冲突,而普通二进制GA移位后还剩3个冲突未解决。由于本文移位算法顾及格式塔原则,因此移位后直线规则排列的建筑物群在移位后仍然保持排列模式不变,符合“连续”性原则,原图中与街道相接的建筑物在移位后仍然与街道相接,也符合“完形”性原则;而普通二进制GA在移位中未顾及格式塔原则,移位后的直线排列建筑物出现了明显的偏移,应与街道相接的建筑物最后也与街道相离。
另外,从图 6中可以看出,建筑物A和B的移位距离特别小(灰色为原始建筑物,黑框为移位建筑物),属于人眼无法感知的尺度。这种在算法模型中的微小移位对整体结果无任何影响,可视为视觉上的无移位,因此算法也很好地顾及了地图感受规律3。

|
| 图 6 地图感受规律3的示意图 Fig. 6 Schematic of Map Feeling Rule 3 |
本文利用实数编码的自适应GA进行建筑物群的地图综合移位研究,并在移位中顾及格式塔原则的保护。实验结果显示,在区域密度较低时,移位效果很好。也就是说,当移位空间充足时,只使用移位就能解决空间冲突。但当建筑物密度较大,很多空间冲突无法通过移位有效解决时,需要加入删除、简化或融合等综合算子。另外,随着建筑物个数的增多,算法搜索空间也越来越大,算法完成时间会越来越长,为了解决这个问题,进一步细分地图要素的移位空间,并引入并行计算等方法是非常必要的。
| [1] | Ruas A. A Method for Building Displacement in Automated Map Generalization[J]. International Journal of Geographical Information Science, 1998, 12(8):789-803 |
| [2] | Ai Tinghua.A Displacement of Building Cluster Based on Field Analysis[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(1):89-94 (艾廷华.基于场论分析的建筑物群的移位[J].测绘学报, 2004, 33(1):89-94) |
| [3] | Fei Lifan, He Jin. Displacement Models for Solving Graphic Conflicts Between Streets and Buildings[J]. Geomatics and Information Science of Wuhan University, 2007, 32(6):540-543 (费立凡, 河津.解决街道与建筑物图形冲突的移位模型研究[J]. 武汉大学学报·信息科学版, 2007, 32(6):540-543) |
| [4] | Fei Lifan. A Method of Automated Cartographic Displacement—On the Relationship Between Streets and Buildings[D]. Germany:University of Hannover, 2002 |
| [5] | Ware J M, Jones C B, Thomas N. Automated Map Generalization with Multiple Operators:A Simulated Annealing Approach[J]. International Journal of Geographical Information Science, 2003, 17(8):743-769 |
| [6] | Wilson I D, Ware J M, Ware J A. A Genetic Algorithm Approach to Cartographic Map Generalization[J]. Computers in Industry, 2003, 52:291-304 |
| [7] | Hojholt P. Solving Space Conflicts in Map Generalization:Using a Finite Element Method[J]. Cartography and Geographic Information Science, 2000, 27(1):65-73 |
| [8] | Harrie L E. The Constraint Method for Solving Spatial Conflicts in Cartographic Generalization[J]. Cartography and Geographic Information Science, 1999, 26(1):55-69 |
| [9] | Bader M. Energy Minimization Methods for Feature Displacement in Map Generalization [D]. Switzerland:University of Zurich, 2001 |
| [10] | Bader M, Barrault M, Weibel R. Building Displacement over a Ductile Truss[J]. International Journal of Geographical Information Science, 2005, 19(8/9):915-936 |
| [11] | Li Z, Yan H, Ai T, et al. Automated Building Generalization Based on Urban Morphology and Gestalt Theory [J]. International Journal of Geographical Information Science, 2004, 18(5):513-534 |
| [12] | Wang Xiaoping, Cao Liming. Genetic Algorithm:Theory, Application and Software Implementation[M]. Xi'an:Xi'an Jiaotong University Press Co., Ltd., 2003:18-28(王小平, 曹立明.遗传算法——理论、应用与软件实现[M].西安:西安交通大学出版社, 2003:18-28) |
| [13] | Wang Chengdong, Zhang Youyun.Adaptive Pseudo-Parallel Genetic Algorithm Based on Real Coding[J]. Journal of Xi'an Jiaotong University, 2003, 37(7):7-10(王成栋, 张优云. 基于实数编码的自适应伪并行遗传算法[J]. 西安交通大学学报, 2003, 37(7):7-10) |
 2015, Vol. 40
2015, Vol. 40



