文章信息
- 靳凤攒, 应申, 李霖, 郭仁忠
- JIN Fengzan, YING Shen, LI Lin, GUO Renzhong
- 三维几何体的验证规则及修复方法研究
- Validation Rules and Repairing True 3D Solids
- 武汉大学学报·信息科学版, 2015, 40(2): 258-263
- Geomatics and Information Science of Wuhan University, 2015, 40(2): 258-263
- http://dx.doi.org/10.13203/j.whugis20130527
-
文章历史
- 收稿日期:2013-09-24
2. 深圳市规划和国土资源委员会, 广东 深圳 518034
2. Urban Planning, Land and Resources Commission of Shenzhen Municipality, Shenzhen 518034, China
随着城市的立体开发,已经有越来越多的应用依赖于三维数据,如三维地籍[1, 2]、城市规划[3],但仅仅有三维空间数据并不能满足现实世界的需要,如必须用真三维几何体表达一座建筑,才能保证其内部连通进而计算其体积,才能计算城市建筑物的能量耗费量(如热能)[4],并且相邻的建筑单元之间只能共享面片(墙)而不允许相互空间的渗透[5],这就要求三维数据构成的三维体是封闭的。于是人们开始关注真三维几何体的创建,如三维城市中,用推拉拔高方法来生成三维城市模型体[6, 7, 8]。当前众多基于立面(facade)的城市三维建模仅仅具有三维空间坐标,本质上还是离散的面片,不具有严格的几何和拓扑意义上三维体的概念[9]。要想创建真三维几何体,必须明晰真三维几何体所满足的条件;而当前对如何构建三维几何体,如何确定其有效性或验证规则的研究还很少见。本文首先描述了三维几何体的概念,重点从三维几何体的点、边、面、体四个维度层面探究了三维几何体所要满足的规则,并进一步研究根据这些规则如何去验证和修复三维空间中已存在的三维数据来满足三维几何体。
1 三维几何体概念的相关研究
目前,三维几何体定义主要有3类:① ISO19107和GML中三维几何体的定义[10, 11]:体是三维几何的基础,它是由一系列边界面(壳)来定义的,作为边界的面不允许自邻接且是2流形的(2-manifold)。② 计算机几何学中三维几何体是由点、边、面及其之间的相互关系组成的[11],三维实体的表面边界是一个有向的封闭的二维流形,其拓扑关系通常使用半边数据结构进行表达,每一个边都是由两个不同方向的半边表达的;面是由半边沿着边界循环围成的[12]。③ Oracle中三维体的定义是由一个外部边界面和0个或多个内部边界面组成的,为了区分实体的内部和外部,规定外部边界面的法向总是从体的内部指向外部[13],其定义本质上是基于ISO191072。这些定义都不支持带洞的多面体、奇异的形状等非2流形的形体和对象,而现实世界中的对象很多是这种特殊体[14],因此前述三维体的定义很难满足三维地籍建模的需要[2, 15]。
文献[9, 16]中定义三维几何体的核心规则是:内部连通、封闭、边界面是2流形的。考虑到现实中三维形体的形状(如三维地籍中的实体[15])有较多的非2流形,本文定义的三维几何体是由一系列二维边界面片形成的封闭形体,该形体须保持体内部的三维空间连通性。2流形中具有边或线只使用2次的规则,本定义打破了2流形的简单性:该三维体的边界面可以自邻接,三维体的外部可形成三维洞。在非2流形的三维体中,很难确定点或边的哪侧是三维体的内部,如图 1(a)所示的同一个三维体的奇异点、图 1(b)中的边AB被使用了4次,这种基于点或边自邻接的非2流形在本文的定义中仍是有效的三维体,因为它保持着三维体内的空间连通性。
上述复杂三维体的构建是传统2流形所不能实现的,不仅仅表现在基于点和边的奇异性(图 1)上,更重要的体现在对“洞”的定义和处理上。根据2流形的定义,若三维体是由带洞的面构成,则每个带洞的面在二维平面中都要被处理,通过增加一个虚构的边来使其满足2流形的要求[10, 17]。很明显,这种处理方法无法在数据处理的整个过程中保持几何数据的不变性和一致性,它随时增加了新的边数据。事实上,在现实生活中,有许多不规则形状的三维建筑物自邻接或有穿透洞(图 1(c)、1(d))等,它们仍保持三维空间内部的连通性,而此类非流形的实体也是有效的。本文定义的三维体无2流形的限制,可以极大地满足现实世界中的非流形三维体。

|
| 图 1 非流形的三维几何体 Fig. 1 Non-manifold 3D Solid |
几何定位可定量地描述空间对象,但很难描述空间对象之间的位置关系。拓扑关系可定性地描述空间对象,在相对位置关系方面有很强的稳定性。事实上,拓扑关系是由几何关系产生的,且在一个非几何空间内无法获得拓扑关系[18]。因此,针对三维几何体及其构造,可从几何定位和拓扑关系两个角度来描述三维几何体(S)及其内部构造的点(V)、边(E)、面(F)所需要满足的规则。为便于描述,首先假设在一个三维几何体存在的前提下,该三维几何体内的点、边、面和体的一些基本符号表示: dV/E和dV/F分别表示一个三维几何体内与某个几何点相关联的几何边和几何面的个数; dE/F和dE/V分别表示一个三维几何体内与某个几何边相关联的几何面和几何点的个数; dF/V、dF/E和dF/S分别表示一个三维几何体内与某个几何面相关联的几何点、几何边以及几何体的个数。
2.1 三维几何体中点、边需要满足的规则
规则1
规则2 ∀dV/E≥3,即与三维几何体中任一几何点相关联的几何边的个数至少为3。
规则3 ∀dV/F=dV/E,即与三维几何体中任一几何点相关联的几何面的个数dV/F和与该点相关联的几何边的个数dV/E是相等的。根据规则2,可得dV/F≥3。
规则4 ∀dE/F≥2,即三维几何体内与任一几何边相关联的几何面的个数至少为2。这说明三维几何体中的相邻面都是通过边进行“拼接”关联的,并且支持流形和非2流形的三维体(图 1)。 2.2 三维几何体中面需要满足的规则
规则5 三维几何体中的面片为直面片,即边界线为直线段,面片上的点都必须在同一个平面上,曲面可以被划分成多个直面片 。
规则6 三维几何体中面片的边界必须是封闭的:∀F=(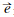 1,
1,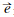 2…,
2…,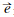 n),有
n),有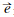 1+
1+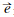 2+…+
2+…+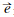 n=
n=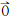 [10, 20],这里假设
[10, 20],这里假设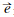 1=(V1,V2),
1=(V1,V2),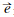 2=(V2,V3),
2=(V2,V3),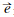 n=(Vn,V1)。
n=(Vn,V1)。
规则7 最大分割原则:设∃F1∩F2≠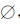 ,则有F1∩F2=E。如图 2所示,FABCD∩FEFGH≠
,则有F1∩F2=E。如图 2所示,FABCD∩FEFGH≠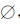 ,则必然存在边MN。同样,∃EAC∩EEG≠
,则必然存在边MN。同样,∃EAC∩EEG≠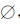 ,有EAC∩EEG=VM。即三维空间中边、面之间都是实交并被分割的。
,有EAC∩EEG=VM。即三维空间中边、面之间都是实交并被分割的。
|
| 图 2 面片和边的最大分割 Fig. 2 Maximal Segmentation of Faces and Edges |
规则8 三维几何体中的面满足dF/V=dF/E,即与三维几何体中任一几何面相关联的几何点的个数dF/V和与该面相关联的几何边的个数dF/E是相等的。
规则9 面片的单向使用原则:根据一定法则(如右手法则)可确定面片的正、负法方向,一个面片的正、负法方向不同时参与一个三维体的构造。因此,一个三维体自邻接时不能共享同一个几何面片。
2.3 三维几何体需要满足的规则
一个三维几何体不仅需要三维几何体构造中的点、边、面满足上述规则,而且从三维几何体的角度还需要满足以下规则。
规则10 三维几何体中点、边、面都是三维几何体构造的一部分,即V,∃E使V∈E;E,∃F使E∈F;F,∃s使F∈s;s,∃S使s∈S,其中s是三维几何体的外壳或边界面[21],S表示三维几何体。
规则11
规则12 三维几何体具有内部连通性,也就是说,体内任意两点间存在一个内部路径,且该路径不与体的边界(几何面或边)相交。如果一个几何体满足封闭性和面的单向使用性原则,那么其必然满足内部连通性。
规则13 ∃S1,S2,如果S1、S2相邻接,那么相邻接的部分只能是点、边或面,且共享它们,而不能产生新的几何元素,否则三维体的几何数据将重组。同时一个三维体可自邻接于内部构造的几何点、边,如图 1(b)中三维体自邻接于一条线。
规则14 ∃S1,S2,如果S1∩S2≠ ,则S1∩S2和S1∪S2仍然是三维几何体,即三维体的交非空时(不包括相互邻接的三维体),它们的交和并仍为三维体。
,则S1∩S2和S1∪S2仍然是三维几何体,即三维体的交非空时(不包括相互邻接的三维体),它们的交和并仍为三维体。
必须注意的是,上述规则是必要的,但不是充分的,并且这些规则也不可能是详尽的,还可能会有另外的一些规则来验证三维体。因此,这些规则并不具有完备性。
3 三维几何体的验证与修复
原则上,三维几何体所具有的规则都可以用来验证体的有效性。但是由于几何数据组织和处理的差别,不能满足上述规则时,需采取相应方法进行修复,只有这样才能更好地利用已有的三维数据去创建三维体。下面就依据上述规则讨论如何验证三维空间中“已假设存在的体”是不是真三维体,当不满足要求时,进行一定的修复。
3.1 三维几何体中点、边、面的验证与修复
1) 依据规则1,如果X1=X2&&Y1=Y2&&Z1=Z2,说明两个点完全重叠,则需要删除其中一个点。
2) 依据规则6,如果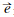 1+
1+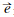 2+…+
2+…+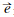 n≠
n≠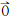 ,则这个面不是封闭的。因为三维几何体中的点都满足点的唯一性原则,又根据规则5,面上的点都在一个平面内,所以只能是构成体的某个面的边界线不封闭。如图 3所示,顶面V1没有闭合到V5处,同时V5已经参与侧面的构造,因此修复时,应将V1归一到V5处,完成对顶面和正面的修复。
,则这个面不是封闭的。因为三维几何体中的点都满足点的唯一性原则,又根据规则5,面上的点都在一个平面内,所以只能是构成体的某个面的边界线不封闭。如图 3所示,顶面V1没有闭合到V5处,同时V5已经参与侧面的构造,因此修复时,应将V1归一到V5处,完成对顶面和正面的修复。

|
| 图 3 不封闭面的修复 Fig. 3 Fixing Faces via Moving the Vertex |
3) 三维构体中通常存在孤立边、悬挂边、孤立面、悬挂面,需要对它们进行相应处理。
对孤立边EIso=(V1,V2),有dV1/E=1,dV2/E=1,即边的两个端点的度都等于1的边。如图 4中边E(V7,V8)。
对悬挂边EHan=(V1,V2),有(dV1/E=1,dV2/E>1)‖(dV1/E>1,dV2/E=1),构成边的两个端点中,一个端点的度为1,另一个大于1。如图 4中边E(V1,V2)。
对孤立面FIso=(E1,E2,…,En),有dE1/F=dE2/F=…=dEn/F=1。如图 4中面F(V3,V4,V5,V6)。
对悬挂面FHan=(E1,E2,…,En),则∃dEi/F>1(i∈(1,2,…,n)),∃dEj/F=1(j∈ 1,2,…,n 且j≠i)。即与度为1的边关联的面片是孤立面或悬挂面;若该面片的其他边的度都为1,则其为孤立面,否则为悬挂面。如图 4中面F(V9,V10,V11,V12)。
依据规则3、8,判断dV/F和dV/E、dF/V和dF/E是否相等,如果不相等,那么在该三维体中肯定存在悬挂边、悬挂面、孤立边或孤立面,需要采用如下的方法进行修复:①计算dV/E和dE/F的值,找出所有的FIso、FHan、LIso、LHan并删除,注意操作顺序:先删除面片,然后删除边。②更新三维体数据,重新计算三维体数据中dV/E和dV/F的值,检查是否依然存在LIso、LHan、FIso、FHan。③如果依然存在FIso、FHan、LIso、LHan,则将其删除,并返回步骤②,否则结束。
以图 4(a)为例:① 计算图 4(a)中所有的dV/E和dE/F值,E(V1,V2)中dV1/E=2,dV2/E=1,属于悬挂边;E(V7,V8)中dV7/E=dV8/E=1属于孤立边,将E(V1,V2)和E(V7,V8)删除。② 重新计算删除边E(V1,V2)和E(V7,V8)后的三维体数据中的dV/E和dE/F的值,所有的dV/E>3,dE/F>2。③ 根据步骤②判断三维体数据中不再存在悬挂边、孤立边等,修复结束。
依据规则2、4:dV/E≤3的点都不满足三维体中点数据的要求,但是这些不符合要求的点是由于边或面不符合要求引起的(如上述悬挂边、悬挂面),在进行处理时,要采用自上而下的原则,即先处理面数据,之后是线数据。
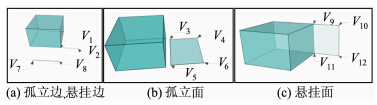
|
| 图 4 孤立边、悬挂边、孤立面、悬挂面 Fig. 4 Isolating Edge and Dangling Edge, Isolating Face and Dangling Face |
4) 依据规则7:三维体中边和面要满足最大分割原则,最大分割后边、面的确定性以及规则9的约束可以有效地避免麦比乌斯(Mbius)曲面及克莱因(Klein)瓶的情形。
5) 依据规则9:一个三维几何体不允许自邻接于面,如果自邻接于面,就应该剔除那个共享面。如图 5中FABCD(又称内部面)应该删除,因为它违反了面的单向性原则。

|
| 图 5 不合规则的内部面片 Fig. 5 Inner Face Contained Within a Solid |
6) 三维中的二维环或洞R[2]的判定依赖于三维体的环境。如图 6(a)中体 S1顶面上的面R只属于S1,所以顶面上的面R不是洞,或者说R也参与三维体的构建并指向体S1的内部;而在图 6(b)中,体S1顶面的面R同时参与体S1和S2的构造,则S2中的R对S1来说就是一个标准的二维洞的概念。

|
| 图 6 二维洞的判定 Fig. 6 Judgement of 2D Ring |
在验证了三维几何体中的点、边、面后,下面进一步对三维几何体进行整体性验证。
1) 依据规则10:如果存在V、E或s不满足规则10中的条件,则说明可能存在孤立边或孤立面,应采用§3.1中的第3个方法修复。
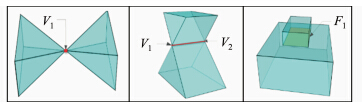
2) 依据规则10、13、14:多个三维体相邻接时应删除重复的几何数据,保证体在拓扑上邻接。如图 7中两个体分别在点、边或面处相邻接,它们共享一个点、边或面。
|
| 图 7 三维体在点、边、面处邻接 Fig. 7 Two Solids Meeting at Vertex,Edge or Face |
3) 欧拉公式(V-E+F=2)说明简单体的顶点数、边数和面数之间的关系;非流形的多面体采用欧拉-庞加莱公式[22]验证:
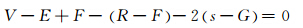
其中,R为二维环;s为壳;G为三维洞。
以图 8为例,说明用欧拉-庞加莱公式验证现实世界中存在的几种常见类型的三维几何体。图 8(a)中边E的个数为24,面F的个数为11,顶点V的个数为16,二维环R的个数为12(11个面加顶面上的一个内部环),壳s的个数为1,三维洞G的个数为0。因此有如下等式:
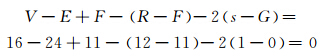
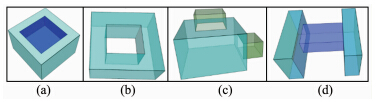
同理,对于图 8(b),E=24,F=10,V=16,R=12,s=1,G=1,有16-24+10- 12-10 -2 1-1 =0;对于图 8(c),E=36,F=16,V=24,R=18,s=1,G=0,有24-36+16- 18-16 -2 1-0 =0;对于图 8(d),E=48,F=20,V=32,R=22,s=1,G=1,有32-48+20- 22-20 -2 1-0 =0。
|
| 图 8 满足欧拉-庞加莱公式的三维体 Fig. 8 Tests of Euler-Poincaré Equation in Several Solids |
二维环R(图 8(a))和穿透洞(三维洞)(图 8(b))在现实对象中很常见(如跨街建筑),因此带洞的三维体是客观的需求。欧拉-庞加莱公式是三维几何体验证的必要非充分条件:如果一个三维对象不满足欧拉-庞加莱公式,则其必不是三维体;但满足欧拉-庞加莱公式并不一定是三维体,如图 4(c)中,E=15,F=7,V=10,R=7,s=1,G=0,有10-15+7- 7-7 -2 1-0 =0,满足欧拉-庞加莱公式,但却不是一个三维体。
3.3 三维几何体的几何化简
三维几何体的几何化简是在保证三维体特征的前提下,减少几何数据的复杂度,简化拓扑表达。如图 9中,FABEF∩FEFCD=EEF,且面FABEF和面FEFCD在同一平面内,那么就需要计算边EEF的dE/F值。
1) 当dE/F=2时,说明EEF由面FABEF和FEFCD共享,且不被其他面占用,则边EEF应该删除(图 9(a))。类似的,如果边EF、EG、GH和HF都被删除掉,则点E、F、G和H也删除,形成边AC、BD(图 9(b))。
2) 当dE/F>2时,说明还有另外一个面(FEFGH)在使用EEF,不能删除。图 9(c)中,EEF∈FABEF,EEF∈FCDEF,EEF∈FEFGH,所以边EEF不能删除,此时图 9(c)中是有2个三维几何体在面FEFGH处相邻接。

|
| 图 9 三维几何体的化简 Fig. 9 Simplification of the Solid’s Geometrics |
由于当前对三维体缺乏明确的定义和约定,无论是初始创建三维拓扑结构,还是事后维护三维拓扑结构,都要面临一些挑战。本文从三维地籍的特殊性出发,给出了一种更满足现实世界对象要求的三维几何体描述。本文认为,拓扑上自邻接于点、线的三维体都是有效的,这样就更有效地支持了现实生活中复杂的三维地籍对象。在此基础上,详细描述了这种三维几何体在几何和拓扑上所需要满足的规则,进而结合实例给出了相应的验证规则和修复方法,从而为构建有效的三维地籍数据并利用这些数据进行三维城市建模和空间分析提供了理论支持。
| [1] | Guo Renzhong, Ying Shen. Three-Dimensional Cadastre Analysis and Data Delivery[J]. China Land Science, 2010(12):45-51(郭仁忠, 应申. 三维地籍形态分析与数据表达[J].中国土地科学, 2010 (12):45-51) |
| [2] | Ying Shen, Li Lin, Guo Renzhong, et al.Design and Development of 3D Cadastral System Prototype Based on the LADM and 3D Topology[C]. The 2nd International Workshop on 3D Cadastres, Delft, The Netherlands, 2011 |
| [3] | Zhou Jingfei. Realize 3D Modeling Method to Large-Scale Buildings in GIS[J]. Geospatial Information, 2011, 9(1):85-88(周靖斐.GIS系统中实现规模化建筑物的三维建模方法[J].地理空间信息, 2011, 9(1):85-88) |
| [4] | Carróin D, Lorenz A, Kolbe T H. Estimation of the Energetic Rehabilitation State of Buildings for the City of Berlin Using a 3D City Model Represented in CityGML[J]. International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, 2010, 38:31-35 |
| [5] | Kolbe T H. Representing and Exchanging 3D City Models with CityGML[M]. Berlin, Heidelberg:Springer, 2009:15-31 |
| [6] | Ying Shen, Li Lin, Guo Renzhong.Building 3D Cadastral System Based on 2D Surveying Plans with SketchUp[J]. Geospatial Information Science, 2011, 14(2):129-136 |
| [7] | Ledoux H, Meijers M.Topologically Consistent 3D City Models Obtained by Extrusion[J]. International Journal of Geographical Information Science, 2011, 25(4):557-574 |
| [8] | Meijers M. Extruding Building Footprints to Create Topologically Consistent 3D City Models[J]. Urban and Regional Data Mangement, 2009, 2 009:39-48 |
| [9] | Guo Renzhong, Ying Shen, Li Lin. Automatic Construction of 3D Valid Solids for 3D Cadastral Objects Based on Facet Sets[J]. Acta Geodaetica et Cartographic Sinica, 2012, 41(4):620-626(郭仁忠, 应申, 李霖.基于面片集合的三维产权体构建[J].测绘学报, 2012, 41(4):620-626) |
| [10] | Kazar B M, Kothuri R, Van Oosterom P, et al.On Valid and Invalid Three-Dimensional Geometries[C]//Advances in 3D GeoInformation Systems. Berlin, Heidelberg:Springer, 2008:19-46 |
| [11] | CGAL, Computational Geometry Algorithms Library[EB/OL].http://www.cgal.org, 2013 |
| [12] | Verbree E, Si H. Validation and Storage of Polyhedra Through Constrained Delaunay Tetrahedralization[M]. Berlin, Heidelberg:Springer, 2008:354-369 |
| [13] | Brugman B A. 3D Topological Structure Management Within a DBMS, Validating a Topological Volume [D]. Delft:Delft University of Technology, 2010 |
| [14] | Gröger G, Plümer L. Topology of Surfaces Modelling Bridges and Tunnels in 3D-GIS[J]. Computer Environment and Urban System, 2011, 35(3):208-216 |
| [15] | Van Oosterom P. Research and Development in 3D Cadastres[J]. Computers, Environment and Urban Systems, 2013, 40:1-6 |
| [16] | Arens C, Stoter J, Van Oosterom P. Modelling 3D Spatial Objects in a Geo-DBMS Using a 3D Primitive [J]. Computers & Geosciences, 2005, 31(2):165-177 |
| [17] | Horna S, Meneveaux D, Damiand G, et al. Consistency Constraints and 3D Building Reconstruction[J]. Computer-Aided Design, 2009, 41(1):13-27 |
| [18] | Kumar, Prasanna N. A Short Note on the Theory of Perspective Topology in GIS[J]. Annals of GIS Ahead-of-Print, 2013, 19(2):123-128 |
| [19] | Van Oosterom P. Axiomatic Definition of Valid 3D Parcels, Potentially in a Space Partition[C]. The 2nd International Workshop on 3D Cadastres, Delft, the Netherlands, 2011 |
| [20] | Van Oosterom P. Validity of Mixed 2D and 3D Cadastral Parcels in the Land Administration Domain Model[C]. The 3rd International Workshop on 3D Cadastres:Developments and Practices, Shenzhen, China, 2012 |
| [21] | Gröger G, Plümer L. How to Achieve Consistency for 3D City Models[J]. Geoinformatica, 2011, 15 (1):137-165 |
| [22] | Wilson P R. Euler Formulas and Geometric Modeling[J]. Computer Graphics and Applications, IEEE, 1985, 5(8):24-36 |
 2015, Vol. 40
2015, Vol. 40



