文章信息
- 黄少滨, 杨欣欣
- HUANG Shaobin, YANG Xinxin
- 基于最小平方和残差的高阶模糊联合聚类算法
- A Minimum Sum-squared Residue for High-order Fuzzy Co-clustering Algorithm
- 武汉大学学报·信息科学版, 2015, 40(2): 238-242
- Geomatics and Information Science of Wuhan University, 2015, 40(2): 238-242
- http://dx.doi.org/10.13203/j.whugis20130094
-
文章历史
- 收稿日期:2013-04-24
近年来,现代信息系统产生了大量包含多种类型数据的数据集,并且不同类型数据之间相互关联[1, 2]。如在论文出版系统中包含4种类型的数据[1, 2],分别是作者、论文、会议和关键词。将这种相互关联的多种类型数据称为高阶异构数据[3, 4]。为了有效挖掘高阶异构数据隐藏的模式,有学者提出了高阶异构数据联合聚类 (简称为高阶联合聚类)方法[3, 4]。已有的高阶联合聚类算法包括基于图划分的方法[3, 5, 6],主要有CBGC[3]和CIHC[6];基于信息论的方法[4, 7],如CIT[4]和AD-HOCC[7];基于k部图学习的方法[8, 9],包括RSN [8]和SKGC[9];基于矩阵分解的方法[1, 2, 10, 11],代表算法有SRC[10]和SS-NMF[11];基于Goodman Kruskal的方法CoStar[12];基于排名的聚类方法,代表算法有NetClus[13]。这些聚类算法都是硬划分方法,一个数据要么“属于”或“不属于”一个聚簇。然而在实际应用中,有些数据同时属于多个聚簇,聚簇结构之间存在重叠的部分,硬划分方法并没有考虑这种聚簇重叠问题。为此,本文提出了一种基于最小平方和残差的高阶模糊联合聚类算法(minimum sum-squared residue for high-order fuzzy co-clustering,MSR-HFCC)。MSR-HFCC算法利用平方和残差衡量不同聚簇数据之间关系的相异度[14, 15],评估聚类质量。为了更好地描述重叠聚簇的聚类结果[16, 17],在平方和残差中引入模糊概念,将聚类问题转化为最小化模糊平方和残差的优化问题。
1 MSR-HFCC算法 1.1 MSR-HFCC算法目标函数
由X1={x11,…,xn11},X2={x12,…,xn22},…,Xm={x1m,…,xnmm}共m种类型数据组成高阶异构数据,ni(1≤i≤m)表示第i种类型数据Xi的数据个数。Xi与Xj的关系矩阵是 D (ij)=(dpq(ij))ni×nj,p行q列元素dpq(ij)表示xpi与xqj之间的关系强度。设Xi(1≤i≤m)划分为Ki个聚簇,残差hpqkikj(ij)是一种衡量关系dpq(ij)与xpi和xqj所在聚簇内所有数据之间的关系相异度的指标[14, 15]。高阶联合聚类的目标是寻找每种类型数据最优的划分,使得不同聚簇内数据之间的关系相异度最低。可见,高阶联合聚类问题可以转化为不同聚簇内的数据之间关系残差hpqkikj(ij)的平方和最小化问题。另外,MSR-HFCC算法利用隶属度描述对象属于某聚簇的程度。其目标函数定义如下:
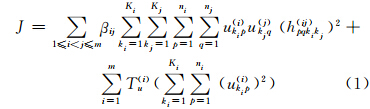
式中,βij为数据{Xi,Xj}之间关系的权值,满足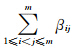 =1;隶属度ukip(i)满足如下限制条件:
=1;隶属度ukip(i)满足如下限制条件:
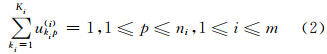
数据项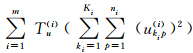 为模糊项;Tu(i)为模糊度参数,用于调节隶属度ukip(i)的模糊程度;关系强度dpq(ij)的残差hpqkikj(ij)有如下两种定义方式[14, 15]:
为模糊项;Tu(i)为模糊度参数,用于调节隶属度ukip(i)的模糊程度;关系强度dpq(ij)的残差hpqkikj(ij)有如下两种定义方式[14, 15]:
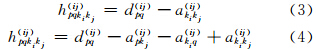
其中,
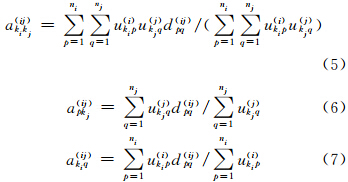
通过拉格朗日乘子法求解ukip(i)的更新规则,构造如下拉格朗日函数:
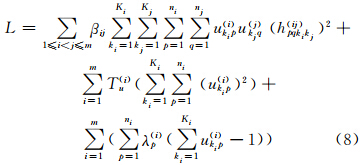
其中,λp(i)为对应限制条件(2)的拉格朗日乘子。由拉格朗日最优解的必要条件,分别求L关于λp(i)和ukip(i)的偏导数,并令其为零,则:
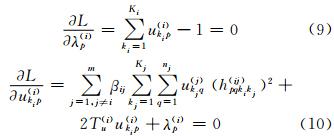
结合式(9)和式(10)可得ukip(i)的更新迭代规则:
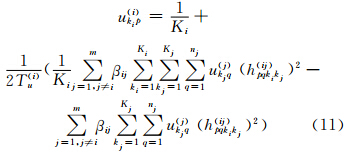
综上所述,根据式(3)、式(4)两种残差计算方式,设计MSR-HFCC算法的两种计算形式MSR-HFCC_H1和MSR-HFCC_H2。其中,MSR-HFCC_H1算法的计算步骤描述如下:

MSR-HFCC_H2与MSR-HFCC_H1的计算步骤类似,不同之处在于MSR-HFCC_H2利用式(5)、式(6)、式(7)和式(4)分别更新 (akikj(ij))τ+1、(apkj(ij))τ+1、(akiq(ij))τ+1和(hpqkikj(ij))τ+1。
根据式(11)计算ukip(i)的时间复杂度为O(niKi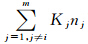 ;根据式(5)、式(6)、式(7)计算akikj(ij)的时间复杂度分别为O(ninj)、O(nj)和O(ni)。高阶异构数据涉及m种类型的数据,MSR-HFCC_H1和MSR-HFCC_H2的时间复杂度均为
;根据式(5)、式(6)、式(7)计算akikj(ij)的时间复杂度分别为O(ninj)、O(nj)和O(ni)。高阶异构数据涉及m种类型的数据,MSR-HFCC_H1和MSR-HFCC_H2的时间复杂度均为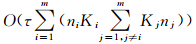 ,τ其中τ为迭代次数。
,τ其中τ为迭代次数。
2 实验分析 2.1 数据集
采用文献[13]的方法,利用Cora论文数据集,由会议、论文和单词组成高阶异构数据集T1和T2,每个类别包含300篇论文;采用文献[12]的方法,利用Corel图像数据集,由图像、单词和图像分割组构建高阶异构数据集I1和I2,每个类别包含100张图像;采用文献[5]的方法,利用IAPR TC-12 Benchmark数据集,由图像、特征和单词构建高阶异构数据集P1,每个类别包含300张图像。论文和图像类别、单词数见表 1。
| 简称 | 数据集 | 单词数 | 类别 |
| T1 | Cora | 2 000 | database,artificial intelligence |
| T2 | Cora | 2 000 | operating systems ,architecture |
| I1 | Corel | 116 | cow,grass,horses |
| I2 | Corel | 114 | tree,bird,sky |
| P1 | IAPR | 1 000 | traveler,animal |
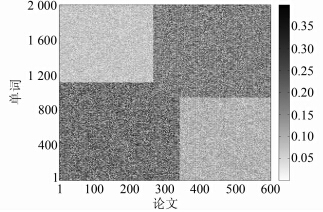
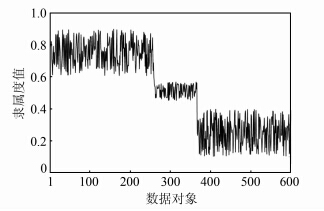
图 1为MSR-HFCC算法在I1数据集上挖掘的聚簇结构可视化结果,可以看出存在明显的 聚簇重叠结构,T1、T2、I2和P1数据集中也具有类似的现象。图 2为P1数据集中图像对于第一个聚簇的隶属度值,260~376之间的图像为聚簇重叠部分,隶属度值接近于0.5。表 2为P1数据集中聚簇重叠部分图像的隶属度示例。这些图像既属于traveler聚簇,又属于animal聚簇,因此难以严格地将数据划分到traveler聚簇或者animal聚簇中。可见,MSR-HFCC_H算法更客观地描述了现实世界数据的聚类结果,能够有效地分析具有聚簇重叠结构的数据。
|
| 图 1 聚簇结构可视化结果 Fig. 1 Results of Visual Cluster Structures |
|
| 图 2 P1数据集图像隶属度值分布 Fig. 2 Distribution of Memberships of Images in P1 Dataset |
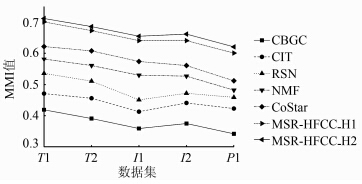
将MSR-HFCC_H1和MSR-HFCC_H2算法与目前已有的5种“硬划分”高阶联合聚类算法进行准确率对比,包括CBGC[3]、CIT[4]、RSN[8]、NMF[11]和CoStar[12]。图 3所示为以上算法聚类结果的正则化互信息(normalized mutual information,NMI)值。首先,MSR-HFCC_H1和MSR-HFCC_H2算法的聚类结果明显优于目前已有的5种“硬划分”高阶联合聚类算法,这一定程度上是由于模糊方法能更有效地描述具有重叠聚簇结构数据的聚类结果。其次,MSR-HFCC_H2算法的聚类结果略优于MSR-HFCC_H1的。其原因在于MSR-HFCC_H2算法在计算残差时不仅考虑了某对数据之间的关系与数据所在聚簇内其他关系的差异,而且考虑了与此对数据相关的其他关系的差异。
|
| 图 3 不同算法聚类结果的NMI值 Fig. 3 NMI Values of Clustering Results |
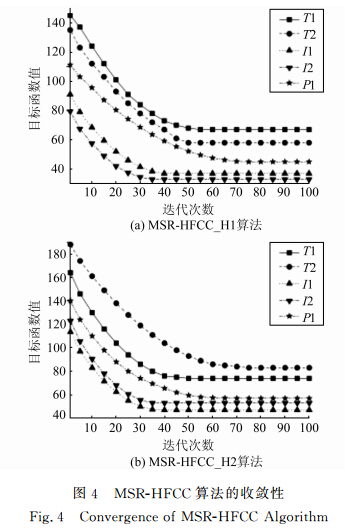
从图 4可以看出,MSR-HFCC_H1和MSR-HFCC_H2算法在5个数据集上迭代40次左右达到收敛状态,具有较好的收敛性。
|
| 图 4 MSR-HFCC算法的收敛性 Fig. 4 Convergence of MSR-HFCC Algorithm |
本文提出了基于最小平方和残差的高阶模糊联合聚类算法MSR-HFCC_H1和MSR-HFCC _H2,该算法能够更有效地描述和分析具有聚簇重叠结构的高阶异构数据,获得更加符合实际的聚类结果。
| [1] | Wang Hua, Nie Feiping, Huang Heng, et al.Nonnegative Matrix Tri-Factorization Based High-Order Co-clustering and Its Fast Implementation[C].The 11th IEEE International Conference on Data Mining, Arlington, USA, 2011 |
| [2] | Wang Hua, Nie Feiping, Ding C.Simultaneous Clustering of Multi-type Relational Data via Symmetric Nonnegative Matrix Tri-factorization[C].The 20th ACM International Conference on Information and Knowledge Management, Glasgow, UK, 2011 |
| [3] | Gao Bin, Liu Tieyan, Zheng Xin, et al.Consistent Bipartite Graph Co-Partitioning for Star-Structured High-Order Heterogeneous Data Co-Clustering[C].The 11th ACM SIGKDD International Conference on Knowledge Discovery in Data Mining, Chicago, USA, 2005 |
| [4] | Liu Tieyan, Ma Weiying.Star-Structured High-Order Heterogenous Data Co-Clustering Based on Consistent Information Theory[C].The 6th IEEE International Conference on Data Mining, Hong Kong, China, 2006 |
| [5] | Gao Bin, Liu Tieyan, Qin Tao, et al.Web Image Clustering by Consistent Utilization of Visual Features and Surrounding Texts[C].The 13th Annual ACM International Conference on Multimedia, Singapore, 2005 |
| [6] | Rege M, Dong Ming, Hua Jing.Graph Theoretical Framework for Simultaneously Integrating Visual and Textual Features for Efficient Web Image Clustering[C].The 17th International Conference on World Wide Web, Beijing, China, 2008 |
| [7] | Greco G, Guzzo A.Co-clustering Multiple Heterogeneous Domains:Linear Combinations and Agreements[J].IEEE Transactions on Knowledge and Data Engineering, 2010, 22(12):1 649-1 663 |
| [8] | Long B, Wu Xiaoyun, Zhang Zhongfei, et al.Unsupervised Learning on K-Partite Graphs[C].The 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Philadelphia, USA, 2006 |
| [9] | Shao Jian, Yin Wentao, Ma Shuai, et al.Topic Discovery of Web Video Using Star-Structured K-Partite Graph[C].The International Conference on Multimedia, Firenze, Italy, 2010 |
| [10] | Long B, Zhang Zhongfei, Wu Xiaoyun, et al.Spectral Clustering for Multi-type Relational Data[C].The 23rd International Conference on Machine Learning, Pittsburgh, PA, 2006 |
| [11] | Chen Yanhua, Wang Lijun, Dong Ming.Non-Negative Matrix Factorization for Semisupervised Heterogeneous Data Co-clustering[J].IEEE Transactions on Knowledge and Data Engineering, 2010, 22(10):1 459-1 474 |
| [12] | Dino I, Robardet C, Pensa R G, et al. Parameter-less Co-clustering for Star-Structured Heterogeneous Data[J]. Data Mining Knowledge Discovery, 2012, 26:217-254 |
| [13] | Sun Yizhou, Yu Yintao, Han Jiawei.Ranking-Based Clustering of Heterogeneous Information Networks with Star Network Schema[C].The 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Paris, France, 2009 |
| [14] | Hartigan J A.Direct Clustering of a Data Matrix[J].Journal American Statistical Association, 1972, 67 (337):123-129 |
| [15] | Cheng Yizong, Church G M.Biclustering of Expression Data[C].The 8th International Conference of Intelligent Systems for Molecular Biology, San Diego, USA, 2000 |
| [16] | Zhong Yexun, Hu Baoqing, Qiao Junjun. Fuzzy Clustering of Multi-factors Evaluated System[J]. Geomatics and Information Science of Wuhan University, 2010, 35(6):752-755(钟业勋, 胡宝清, 乔俊军.多因素评价体系的模糊聚类分析[J].武汉大学学报·信息科学学报, 2010, 35(6):752-755) |
| [17] | Kong Lingqiao, Qin Kun, Long Tengfei. Global SST Data Mining Based on Fuzzy Clustering[J]. Geomatics and Information Science of Wuhan University, 2012, 37(2):215-219(孔令桥, 秦昆, 龙腾飞.利用二阶模糊聚类进行全球海表温度数据挖掘[J].武汉大学学报·信息科学学报, 2012, 37(2):215-219) |
 2015, Vol. 40
2015, Vol. 40



