文章信息
- 喻敏, 王斌, 王文波, 郑雷
- YU Min, WANG Bin, WANG Wenbo, ZHENG Lei
- 联合EMD与核主成分分析的激光陀螺信号消噪
- Laser Gyro Signal De-noising Based on EMD and Kernel Principal Component Analysis
- 武汉大学学报·信息科学版, 2015, 40(2): 233-237
- Geomatics and Information Science of Wuhan University, 2015, 40(2): 233-237
- http://dx.doi.org/10.13203/j.whugis20130078
-
文章历史
- 收稿日期:2013-04-25
2. 卫星海洋环境动力学国家重点实验室, 浙江 杭州 310012
2. State Key Laboratory of Satellite Ocean Environment Dynamics, Hangzhou 310012, China
激光陀螺是新一代的惯性测量元件,与传统的机械陀螺相比具有很多突出的优点,已经在多个领域获得了广泛的应用。激光陀螺输出信号的精度会对惯性导航系统的对准效率造成直接的影响,由于受内部构造及外部环境等不确定因素的影响,陀螺输出信号中往往含有大量的随机噪声,严重影响其使用精度。如何有效减小陀螺随机漂移,提高信号的输出精度,一直是激光陀螺研究的热点和难点[1, 2]。小波变换具有良好的多分辨率分析特性,可对信号在不同频段、不同时刻进行有效分离,因此在陀螺信号的降噪中得到了广泛的应用[2, 3, 4]。但在应用小波变换对陀螺信号去噪时,受到两个方面的限制:① 小波变换需要预先选定小波基和分解的层数。相同条件下选用不同的小波基和分解层数对去噪结果影响很大[5, 6],这给利用小波进行信号去噪带来了很大的不便。② 小波变换本质上属于带通滤波器,更适用于线性、稳态信号的分解,对于激光陀螺类的非线性、非稳态信号,采用小波降噪后的效果也不是特别理想。
为了分析非线性和非稳态信号,Huang等人提出了一种新的时频分解算法——经验模态分解(empirical mode decomposition,EMD)[7]。EMD是一种数据驱动的自适应信号分解方法,可以将复杂信号分解成一组按频率高低排列的内蕴模态函数(intrinsic mode function,IMF)分量。EMD中的基函数和分解层次不需要事先给定[7, 8],而是根据信号特性通过迭代的方式自适应地产生合适的内蕴模态函数和最佳分解层数。EMD方法已经被用于激光陀螺信号的去噪处理中[9, 10, 11, 12, 13, 14, 15],并取得了较好的去噪效果。为了进一步提高EMD对陀螺信号的降噪效果,本文提出了一种联合核主成分分析(Kernel principal component analysis,KPCA)和EMD陀螺信号的去噪方法。根据IMF中的噪声能量分布模型估算每层IMF中所含噪声的能量;再利用噪声能量和核主成分分析去除IMF中的噪声。本文对激光陀螺测试信号进行了降噪实验,并利用交叠式Allan方差和经度、纬度误差对实验结果进行了分析。与经典的小波降噪法相比,本文方法可以更有效地抑制陀螺随机漂移。
1 基于KPCA和EMD的陀螺信号消噪 1.1 陀螺信号IMF的能量构成模型
激光陀螺信号经EMD分解后,原始信号x(k)可被表示为:

其中,K表示内蕴模态函数IMF的个数;第k层imfk的能量ε(imfk)定义为 [16]ε(imfk)=imfk·imf kT。令 f k=imfk,设 f k= g k+ W k,g k表示imfk中所包含的信号成分,W k表示imfk 中的噪声成分,则有:
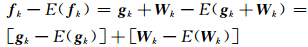
其中,E(·)表示期望。根据零均值高斯分形噪声经EMD分解后的特性可知[16, 17],E( W k)=0。 令
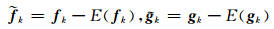
显然,对 f k去噪等价于对 k进行去噪,而
k进行去噪,而  k=
k= 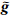 k+ W k,将
k+ W k,将 k、
k、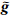 k、 W k的能量分别记为ε(
k、 W k的能量分别记为ε( k)、ε(
k)、ε(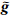 k)和ε( W k),可知,
k)和ε( W k),可知,
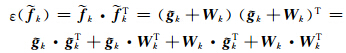
因为信号 g k与噪声 W k无关,所以 ,
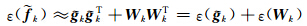
即 k的能量近似等于信号能量ε(
k的能量近似等于信号能量ε( k)与噪声能量ε( W k)之和。对
k)与噪声能量ε( W k)之和。对 k进行去噪时,如果能从
k进行去噪时,如果能从 k中去除能量为ε( W k)的纯噪声,则可认为剩下的部分全部是有用的信号信息,不再含有噪声。但信号
k中去除能量为ε( W k)的纯噪声,则可认为剩下的部分全部是有用的信号信息,不再含有噪声。但信号 k中所含噪声的能量是未知的,通常情况下难以求出
k中所含噪声的能量是未知的,通常情况下难以求出 k中所含噪声的能量ε( W k)的精确值,但通过高斯分形噪声的IMF能量分布模型,可对
k中所含噪声的能量ε( W k)的精确值,但通过高斯分形噪声的IMF能量分布模型,可对 k中噪声的能量ε( W k)进行近似估计。
k中噪声的能量ε( W k)进行近似估计。
1.2 陀螺信号第k层 IMF所含噪声能量的估计
由于陀螺信号中包含大量的有色噪声,因此以高斯分形噪声作为陀螺信号噪声的噪声模型,高斯分形噪声模型可以较好地描述陀螺信号中的有色噪声成分。由文献[16, 17]可知,imfk所含的高斯分形噪声能量ε( W k)和ε( W 1)之间近似满足:

其中,βH按文献[17]所给方法进行计算;
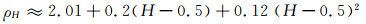
由于含噪信号经EMD分解后,第1层IMF基本由噪声组成[13],因此通常假设ε( W 1)=ε(imf1)。
1.3 利用KPCA对陀螺信号各层IMF去噪时主成分分量的选择
陀螺信号经EMD分解后,估计 imfk中所含噪声的能量ε( W k),本文从噪声能量在信号总能量中所占的比例出发,自适应地确定去噪时所保留的成分分量的取值。令 x = k,则待去噪数据 x = y + W ,x ∈RN,其中, y 为不含噪声的信号数据; W 为信号中所含的噪声。设KPCA去噪中,训练数据集为 x k∈RN,k=1,…,L,其在特征空间F的映射为{Φ( x k)},所用核函数为k( x ,y );映射后,数据{Φ( x k)}的协方差矩阵为 C ,其特征向量为{ V k},则Φ( x )可通过选择前H个合适的主成分分量进行重构:
k,则待去噪数据 x = y + W ,x ∈RN,其中, y 为不含噪声的信号数据; W 为信号中所含的噪声。设KPCA去噪中,训练数据集为 x k∈RN,k=1,…,L,其在特征空间F的映射为{Φ( x k)},所用核函数为k( x ,y );映射后,数据{Φ( x k)}的协方差矩阵为 C ,其特征向量为{ V k},则Φ( x )可通过选择前H个合适的主成分分量进行重构:
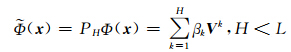
根据KPCA的分解特性可知,Φ( x )中的信号部分主要集中在前若干层的成分分量中,设ΔΦ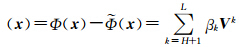 ,则ΔΦ( x )相当于从Φ( x )中删除的噪声。因为{ V k}标准正交,所以,
,则ΔΦ( x )相当于从Φ( x )中删除的噪声。因为{ V k}标准正交,所以,
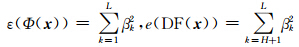
 k在原空间的能量为:
k在原空间的能量为:
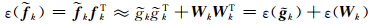
如果选择核函数为多项式核函数,k( x ,y )=(a( x · y )+b)d,并取b=0,a>0,d为正整数,则 k在特征空间的能量为:
k在特征空间的能量为:

因此可以认为,在特征空间中,Φ( k)中信号的能量为E1,而噪声的能量为E2。如果在特征空间中重构Φ(
k)中信号的能量为E1,而噪声的能量为E2。如果在特征空间中重构Φ( k)时,通过选择合适的H,使得删除的噪声ΔΦ(
k)时,通过选择合适的H,使得删除的噪声ΔΦ( k)的能量与Φ(
k)的能量与Φ( k)中所包含的噪声的能量相同,也即在选择H时,使得ε(ΔΦ(
k)中所包含的噪声的能量相同,也即在选择H时,使得ε(ΔΦ( k))=E2,则可认为Φ(
k))=E2,则可认为Φ( k)中的噪声被全部去除,保留下来的主成分分量就是理想的不含噪声的信号。
k)中的噪声被全部去除,保留下来的主成分分量就是理想的不含噪声的信号。
式(2)等价于:

因为 k=
k= k+ W k,因此式(3)等价于:
k+ W k,因此式(3)等价于:

但在选择H 时,很难保证使得式(4)恰好成立,本文中对H 按照以下方法进行取值:如果存在β使式(5)成立,则令H=β,

1) 利用EMD将陀螺信号 x(t)分解为imfk(k=1,2…,N),余项为rN;
2) 令ε(V1)=ε(imf1),对imf1按照SUREShrink阈值方法进行去噪,得到去噪后的值imf′ 1;
3) 取k( x ,y )= a( x · y ) d作为核函数,令 k=imfk-E imfk ,计算imfk中所含噪声的能量ε( W k)(k≥2);
k=imfk-E imfk ,计算imfk中所含噪声的能量ε( W k)(k≥2);
4) 对 k(k≥2)进行KPCA分解,按照式(5)计算在特征空间去噪时应保留的主成分分量的个数H,并通过迭代求其原像
k(k≥2)进行KPCA分解,按照式(5)计算在特征空间去噪时应保留的主成分分量的个数H,并通过迭代求其原像 ′ k;
′ k;
5) imf′ k=  ′ k+E(imfk)即为imfk去噪后的结果,对所有imf′ k进行累加,得到去噪后的陀螺信号
′ k+E(imfk)即为imfk去噪后的结果,对所有imf′ k进行累加,得到去噪后的陀螺信号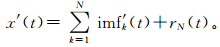 。
。
2 实验分析
本文实验数据来自某次常温(20 ℃)静基座下的激光陀螺漂移测试(标称陀螺漂移为1 °/h),采样间隔为1 s,取x轴的2 000个历元输出信号进行实验分析(y、z轴类似),实验数据如图 1所示。为了比较消噪效果,对陀螺信号分别采用SUREShrink小波阈值法、BayesShrink小波阈值法和本文方法进行去噪。小波阈值去噪中,小波基选用在信号去噪中得到广泛使用的db8小波,分解层数取9,采用硬阈值法去噪。在本文方法去噪中,实验信号经EMD分解后,得到10个IMF分量和一个余项;对各层IMF进行KPCA分解处理时,核函数选k( x ,y )=(a( x · y ))d,取a=2,d=3。

|
| 图 1 激光陀螺原始信号 Fig. 1 Original Signal of Laser Gyro |
激光陀螺漂移信号经SUREShrink小波阈值法、BayesShrink小波阈值法和本文方法去噪后的结果如图 2所示。对比图 2(a)、2(b)和2(c)可以看出,采用本文方法消噪后的信号较小波阈值法消噪后的信号平滑。分别计算原始信号和消噪后信号的均值与方差,结果如表 1所示。可以看出,三种方法消噪后的均值基本相同,但本文方法消噪后的方差更小,表明经本文方法消噪后,陀螺漂移数据中的随机噪声得到了更好的剔除。

|
| 图 2 不同方法去噪结果 Fig. 2 Results of Denoised Signal of Three Methods |
| 原始信号 | SUREShrink 小波 | BayesShrink 小波 | 本文方法 |
| 均值 | 1.922 3 | 1.920 4 | 1.924 1 | 1.917 5 |
| 方差 | 102.974 8 | 2.942 5 | 2.581 6 | 1.199 3 |
为了进一步分析本文方法对陀螺信号的消噪效果,采用交叠式Allan方差对三种方法的消噪结果进行对比分析[18]。设信号的交叠式Allan标准差为σ(τ)(τ=nτ0,τ0为采样间隔),则σ(τ)~τ的双对数曲线可以描述陀螺信号的不同随机误差成分。 用交叠式Allan方差分析法获取原始信号和对三种方法消噪后信号的五项源误差的误差系数,包括量化噪声(Q)、角度随机游走(N)、零偏不稳定性(B)、速率随机游走(K)和速率斜坡(R),结果如表 2所示。三种方法消噪后的经纬度误差[12]见图 3,均方根值(RMS)和最大误差(MAX)如表 3所示。
| Q/μrad | N/(°/h-1/2) | B/(°/h) | K/(°/h3/2) | R/(°/h2) | Q降噪前后比/% | |
| 原始信号 | 6.209 4 | 0.016 5 | 0.317 9 | 2.062 3 | 3.419 2×10-4 | 100 |
| SUREShrink小波 | 0.795 8 | 0.008 3 | 0.184 7 | 0.173 9 | 1.773 2×10-4 | 12.8 |
| BayesShrink 小波 | 0.683 2 | 0.006 4 | 0.130 1 | 0.103 3 | 3.124 7×10-5 | 11.0 |
| 本文方法 | 0.344 6 | 7.882 4×10-4 | 0.089 6 | 0.058 7 | 6.118 3×10-6 | 5.27 |

|
| 图 3 三种方法消噪后的经纬度误差 Fig. 3 Longitude and Latitude Errors After Denoised Signal of Three Methods |
| RMS | MAX | |||
| 经度 | 纬度 | 经度 | 纬度 | |
| SSW | 11.143 4 | 29.585 2 | 21.120 0 | 73.150 0 |
| BSW | 10.114 5 | 26.875 2 | 19.200 0 | 66.500 0 |
| EMD-PCA | 8.079 1 | 21.484 1 | 15.360 0 | 53.200 0 |
从表 2和表 3可以看出,经过三种降噪算法滤波处理后,各项误差系数都有所减小,表明三种方法对陀螺信号都具有一定的消噪作用。与小波阈值法相比,本文方法降噪后信号的各项指标更低,这表明小波消噪后的陀螺信号中仍然含有一定程度的误差成分,而本文方法更进一步地削弱了陀螺信号的各种误差成分。其主要原因是小波阈值消噪方法仅能够去除陀螺信号中白噪声的干扰,但对信号中所含的部分有色噪声难以进行有效去除,限制了小波阈值法的消噪效果。
而EMD-PCA消噪方法通过分形噪声模型估计各层IMF中的噪声能量,可以较准确地估算出IMF中所含的不同噪声的能量总和,因此通过KPCA去除噪声后,可以有效消弱信号中的白噪声成分和有色噪声成分,进一步提高了消噪的效果。从表 2也可以看出,量化噪声是陀螺信号中引入随机误差的主要因素,经SUREShrink小波阈值法、BayesShrink小波阈值法和本文方法降噪后,信号中的量化噪声误差系数分别减小为原来的12.8%、11.00%和5.54%。
3 结 语
本文联合EMD和KPCA提出了一种改进的EMD陀螺信号消噪方法,所提方法中根据陀螺信号各层IMF中所含噪声的能量,自适应地选择IMF经KPCA分解后应保留的主成分分量,从而实现对陀螺信号的消噪。该方法在消噪过程中可根据陀螺信号的自身特性自适应计算模型参数,因此去噪过程仅与陀螺信号的自身特性相关,不需要繁琐的参数和阈值调试。对实测陀螺随机漂移信号进行降噪处理,并通过直接比较法、交叠式Allan方差法和经、纬度误差对不同去噪方法的降噪结果进行比较分析,实验结果表明,与小波消噪方法相比,本文方法的降噪效果有一定程度的提高,可更有效地去除噪声,减少陀螺信号的各项误差成分,提高惯性制导解算的精度。
| [1] | Zhang Chuanbin, Deng Zhenglong. Study on Wavelet Filtering for Signal of Ring Laser Gyro[J]. Acta Electronica Sinica, 2004, 32(1):125-127(张传斌, 邓正隆. 激光陀螺信号的小波滤波方法研究 [J].电子学报, 2004, 32(1):125-127) |
| [2] | Huo Ju, Wang Shijing, Yang Ming. Noise Processing of FOG Signal Based on Wavelet Threshold-Value[J]. Journal of Chinese Inertial Technology, 2008, 16(3):343-347(霍炬, 王石静, 杨明. 基于小波变换阈值法处理光纤陀螺信号噪声[J].中国惯性技术学报, 2008, 16(3):343-347) |
| [3] | Wu Fumei, Yang Yuanxi. GPS/INS Integrated Navigation by Adaptive Filtering Based on Wavelet Threshold Denoising[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(2):124-128(吴富梅, 杨元喜.基于小波阈值消噪自适应滤波的GPS/INS组合导航[J].测绘学报, 2007, 36(2):124-128) |
| [4] | Zhang L, Bao P, Wu X. Multiscale LMMSE-based Image Denoising with Optimal Wavelet Selection[J]. IEEE Transaction on Circuits System Video Technology, 2005, 15(4):469-481 |
| [5] | Zhang Hua, Chen Xiaohong, Yang Haiyan. Optimistic Wavelet Basis Selection in Seismic Signal Noise Elimination[J]. Oil Geophysical Prospecting, 2011, 46(1):70-75(张华, 陈小宏, 杨海燕. 地震信号去噪的最优小波基选取方法[J]. 石油地球物理勘探, 2011, 46(1):70-75) |
| [6] | Flandrin P, Rilling G, Goncalves P. Empirical Mode Decomposition as a Filter Bank[J]. IEEE Signal Processing Letters, 2004, 11(2):112-114 |
| [7] | Xu Xiaogang, Xu Guanlei, Wang Xiaotong, et al. Empirical Mode Decomposition and Its Application[J]. Acta Electronica Sinica, 2009, 37(3):581-585(徐晓刚, 徐冠雷, 王孝通, 等. 经验模式(EMD)分解及其应用[J]. 电子学报, 2009, 37(3):581-585) |
| [8] | Gan Yu, Sui Lifen. De-noising Method for Gyro Signal Based on EMD[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6):745-750(甘雨, 隋立芬. 基于经验模态分解的陀螺信号消噪[J]. 测绘学报, 2011, 40(6):745-750) |
| [9] | Qu Congshan, Yu Hong, Xu Hualong, et al. Random Signal De-noising Based on Empirical Mode Decomposition for Laser Gyro[J]. Infrared and Laser Engineering, 2009, 38(5):859-863(曲从善, 于鸿, 许化龙, 等. 基于经验 模态分解的激光陀螺随机信号消噪[J]. 红外与激光工程, 2009, 38(5):859-863) |
| [10] | Qu Congshan, Lu Tingzhen, Tan Ying. A Modified Empirical Mode Decomposition Method with Applications to Signal De-noising[J]. Acta Automatica Sinica, 2010, 36(1):67-73(曲从善, 路廷镇, 谭营. 一种改进型经验模态分解及其在信号消噪中的应用[J]. 自动化学报, 2010, 36(1):67-73) |
| [11] | Teixeira A R, Tome A M, Stadlthanner K, et al. KPCA Denoising and the Pre-image Problem Revisited[J]. Digital Signal Processing, 2008, 18(4):568-580 |
| [12] | Gan Yu, Sui Lifen, Wang Bing. EMD Threshold De-noising and Its Applications in INS Data Processing[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(4):504-509(甘雨, 隋立芬, 王冰. 经验模态分解阈值消噪方法及其在惯性导航系统数据处理中的应用[J].测绘学报, 2012, 41(4):504-509) |
| [13] | Gan Yu, Sui Lifen, Xiao Guorui, et al. EMD De-noising Theory Considering Static and Dynamic Conditions and Its Application in INS[C].China Statelite Navigation Conference 2013 Provrddinh Proceedings, Wuhan, China, 2013 |
| [14] | Gan Yu.INS Error Processing and Filtering Model Refining for Integrated Navigation Based on Time-frequency Analysis[D]. Zhengzhou:Information Engeering University, 2012(甘雨.基于时频特性分析的INS误差处理及组合导航系统滤波模型精化[D].郑州:信息工程大学, 2012) |
| [15] | Zhang Qiuzhao, Zhang Shubi, Hou Dongyang, et al. FOG Random Sequence Pretreatment Using Empirical Mode Decomposition[J]. Chinese Journal of Sensors and Actuators, 2011, 24(10):1 440-1 444(张秋昭, 张书毕, 候东阳, 等. 基于经验模态分解的光纤陀螺随机序列平稳化处理[J]. 2011, 24(10):1 440-1 444) |
| [16] | Flandrin P, Goncalves P. Empirical Mode Decompositions as Data-driven Wavlet-like Expansions[J]. International Journal of Wavelets Multiresolution and Information Processing, 2004, 2(4):447-496 |
| [17] | Flandrin P, Rilling G, Goncalves P. Empirical Mode Decomposition as a Filter Bank[J]. IEEE Signal Processing Letters, 2004, 11(2):112-114 |
| [18] | Li Xiaoying, Hu Min, Zhang Peng, et al.Applying Overlapping Allan Variance Therry to Better Stochastic Modeling of Microgyro[J]. Journal of Northwestern Polytechnical University, 2007, 25(2):225-229(李晓莹, 胡敏, 张鹏, 等.交叠式Allan方差在微机械陀螺随机误差辨识中的应用 [J].西北工业大学学报, 2007, 25(2):225-229) |
 2015, Vol. 40
2015, Vol. 40


