文章信息
- 李晶, 李冬海, 赵拥军
- LI Jing, LI Donghai, ZHAO Yongjun
- 利用角度和时差的单站外辐射源定位方法
- Single-Observer Passive Coherent Location Estimation Based on DOA and TDOA
- 武汉大学学报·信息科学版, 2015, 40(2): 227-232
- Geomatics and Information Science of Wuhan University, 2015, 40(2): 227-232
- http://dx.doi.org/10.13203/j.whugis20130065
-
文章历史
- 收稿日期:2013-04-22
2. 武汉大学电子信息学院, 湖北 武汉 430079
2. School of Electronic Information, Wuhan University, Wuhan 430079, China
基于外辐射源的无源定位方法又称被动协同定位(passive coherent location,PCL)方法。由于其在航空和电子领域的广泛应用,以及其相比于主动雷达具有体积小、隐蔽性高、低空探测能力等优点[1],近年来成为各研究机构研究的热点。可用于定位的外辐射源包括调频广播 (frequency modulation,FM)[2] 信号、数字电视[1, 3, 4] 信号、手机信号基站WiFi [5]等常见的民用信号。相比于多站系统,单站系统机动性强,不存在时间和数据同步的问题。因此,研究高精度的单站外辐射源定位方法具有重要的意义。
对于固定目标的探测,主要包括接收信号强度(received signal strength,RSS)[6]、信号到达角度(direction of arrival,DOA)[6, 7, 8]和时差(time different of arrival,TDOA)[9]三种主要方法。RSS算法根据信号能量获取目标位置,但信号衰退限制了其精度的提高。DOA方法不可用于单站系统。对于TDOA方法,时差的一种定义为信号从目标到达不同观测站的时间差,文献[10]给出了这类算法的主要求解方法,但此类方法不适用于单站模型;另一种定位为经目标反射的回波与直达波的时间差,文献[11]提出了一种两步估计(two step estimation,TSE)算法,估计结果接近克拉美罗界(Cramer-Rao bound,CRB)。但当TDOA测量误差较大时,TSE不能得到精确的目标位置估计。 文献[12]研究了联合DOA和TDOA对目标辐射源定位的算法,并验证了联合算法的稳定性和定位精度均优于仅一种信息的定位算法。本文联合角度和时差信息,通过外辐射源估计固定目标位置的近似最大似然解。通过构建观测误差的概率密度函数,用牛顿迭代法求解函数的极值点得到目标位置的高精度估计,迭代初值由最小二乘法得到。
1 单站PCL定位模型
本文研究的三维单站外辐射源定位系统如图 1所示。
假设观测站位于坐标原点 X R=[0,0,0]T,目标位置为 X =[x,y,z]T,辐射源位置为 X Trk=[xk,yk,zk]T,辐射源到观测站的距离为dk= 假设观测站到目标的方位角和俯仰角分别为θ和φ,根据目标和观测站位置间的关系,建立角度观测方程:
综合式(1)~式(3),得到系统的观测方程为:
式中,观测量 Θ =[θ,φ,τ1,…,τN]T;观测误差 V =[vθ,vφ,vτ1,…,vτN]T。
2 定位算法
假设观测量的误差是均值为零、方差分别为 σθ2、σφ2、στ12、…、στN2的高斯白噪声,误差的协方差矩阵 PV =diag(σθ2,σφ2,στ12,…,στN2),则其概率密度函数为:
目标位置的最大似然解为:
式(6)等价于:
由于h( X )是非线性方程,X 不能得到解析解。本文采用牛顿迭代法求解 其中, 为了简化等式结构,令R2= 令 牛顿迭代法需要给定初值,否则算法容易陷入局部最优,不能得到正确位置的估计结果。本文采用最小二乘法实现目标位置的粗估计,其结果作为牛顿迭代的初值。
2.2 最小二乘法定位
最小二乘法是最常用的线性参数估计方法[13]。给定向量 b 和矩阵 A ,求解方程 HX = b 。那么,需要对测量方程进行线性化处理。根据模型对R2-rk2进行因式分解,并展开得:
结合式(1),化简式(12)得:
将式(13)和式(1)相加,得:
由式(3)可得 综上所述,目标位置估计分两步实现,首先由式(15)得到最小二乘解,然后通过式(8)迭代得到近似最大似然解。其中,
对式(5)取对数并对 X 求导,得:
因为待估计参数为目标的三维位置坐标,所以系统的CRB是3×3的Fisher信息矩阵(Fisher information matrix,FIM)[13],设为 J。则
那么系统估计误差满足:
其中,
对式(4)的观测量微分得:
其中,H X 、 H X Trk、 H X R分别为h( X )对 X 、 X Trk、 X R的偏导。
其中,
那么可得:
由式(19)可得:;
假设测量误差、站址误差之间互不相关,且均值为零,测量误差协方差矩阵为 P V ,辐射源站址误差协方差矩阵为 P XTrk,观测站站址误差协方差矩阵为 P X R。令 那么目标定位的几何精度因子(geometric dilution of precision,GDOP)为:
为了证明理论分析的正确性,系统仿真实验包含5个外辐射源,辐射源的位置坐标见表 1,辐射源和观测站站址坐标误差均为30 m。
假设目标位于(140,120,10) km,角度的标准差变化范围为 σθ=σφ=10-4~10-2,时差的标准差范围为στ=10-7~10-4。在仿真实验中,每个实验作5 000次蒙特卡洛仿真。
仿真1 TDOA系统与联合DOA和TDOA系统的CRB对比,仿真结果如图 2所示。联合DOA和TDOA的系统在相同时差误差条件下的CRB低于TDOA系统;随着角度误差的增大,联合DOA和TDOA系统的CRB接近TDOA系统,角度误差与时差误差的比值增大时,联合DOA和TDOA系统的CRB偏离TDOA系统。
仿真2 在不同角度误差和时差误差条件下的目标定位结果如图 3所示,可见,本文算法的估计结果在不同的角度误差条件下接近CRB,即使在参数测量误差较大的条件下,也能够实现对目标位置的高精度估计。当时差误差较小时,目标位置估计误差将偏离CRB,且当角度误差比较大时,目标位置估计误差偏离CRB的对应TDOA的误差越大。出现目标位置估计误差偏离CRB的原因是因为观测误差较小时,站址误差的随机性影响了观测误差的随机性。当观测误差较大时,位置误差较大,站址误差对目标位置的估计精度可以忽略,而当观测误差较小时,位置误差较小,站址误差对目标位置的估计精度不可忽略,从而出现偏离CRB的现象。
仿真3
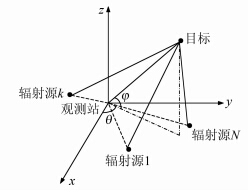
图 1 单站PCL定位系统
Fig. 1 Single-Observer PCL System
 ,目标到观测站的距离为R=
,目标到观测站的距离为R=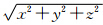 ,辐射源到目标的距离为rk=
,辐射源到目标的距离为rk=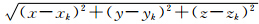 ,信号直达波与经目标反射的回波时间差为τk,其中k=1,…,N,N为辐射源个数。根据模型可建立TDOA观测方程:
,信号直达波与经目标反射的回波时间差为τk,其中k=1,…,N,N为辐射源个数。根据模型可建立TDOA观测方程:


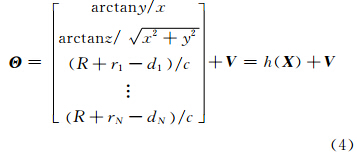
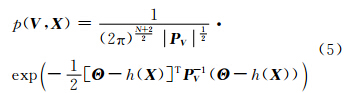

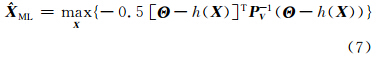
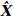 。令F( X )=
。令F( X )= ,则牛顿迭代法求解[7]为:
,则牛顿迭代法求解[7]为:
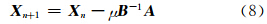
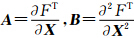 ;μ为迭代步长,且满足0<μ≤1。
;μ为迭代步长,且满足0<μ≤1。
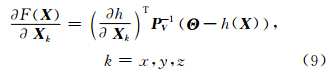
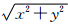 ,对式(4)求导可得:
,对式(4)求导可得:
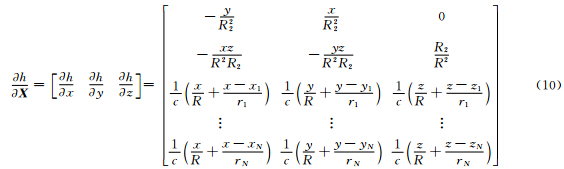
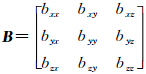 ,其中,
,其中,
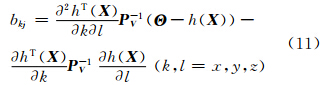
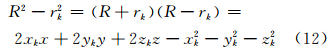
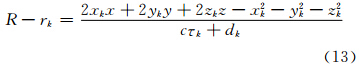

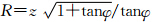 ,并代入式 (14)移项,联合式(2)和式(3)可得到以目标位置为未知参数的线性方程 HX = b ,
且其最小二乘解[7]为:
,并代入式 (14)移项,联合式(2)和式(3)可得到以目标位置为未知参数的线性方程 HX = b ,
且其最小二乘解[7]为:




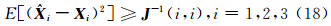
 为估计值
为估计值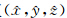 ;
J -1(i,i)为 J 的逆矩阵的第i个对角元素。
;
J -1(i,i)为 J 的逆矩阵的第i个对角元素。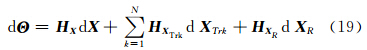

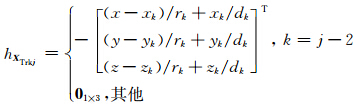



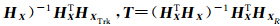 ,则有:
,则有:
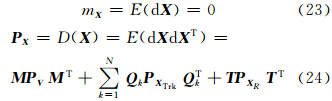
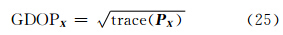
x坐标 y坐标 z坐标
辐射源1
-100
0
1.5
辐射源2
-100
0
2
辐射源3
0
100
1.5
辐射源4
0
-100
2
辐射源5
100
100 2
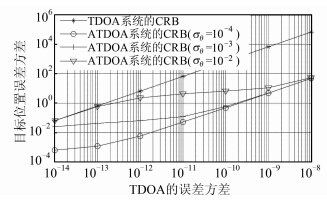
图 2 联合角度和时差定位系统与TDOA定位系统的CRB对比
Fig. 2 CRB of Jointing TDOA and DOA System and TDOA-only System

图 3 在不同角度误差条件下的系统ML解
Fig. 3 Target Position Estimation of ML Method with σθ=10-3and σθ=10-2
|
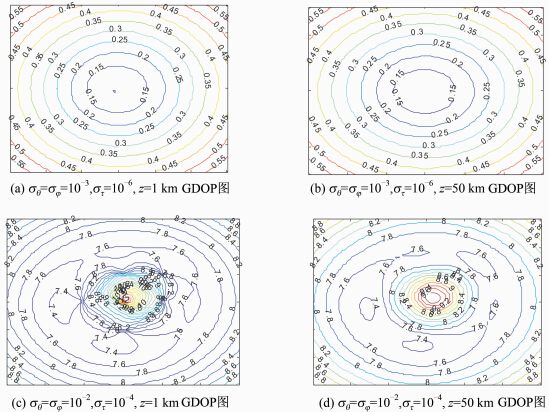
| 图 4 在不同时差误差条件下的GDOP图 Fig. 4 GDOP Figures with Different Time Delay Errors |
本文研究了单站外辐射源对固定目标定位的问题,有效利用多个外辐射源,通过最大似然方法 实现对目标位置的估计。针对系统观测方程非线性的问题,采用牛顿迭代法求解目标位置的最大似然解,迭代初值由最小二乘法得到。通过实验仿真验证了联合角度和时差定位系统的CRB低于相同时差误差条件下的TDOA系统。本文算法可以得到目标的精确估计,误差均方差接近CRB。并通过GDOP图分析了影响定位精度的主要因素包括目标位置、量测误差、辐射源位置和辐射源个数。
| [1] | Alfonso F, Heiner K. Guest Editorial Special Issue on Passive Radar (Part I)[J]. IEEE Aerospace and Electronic Systems Magazine, 2012, 27(10):5 |
| [2] | Belfiori F, Monni S, van Rossum W, et al. Antenna Array Characterisation and Signal Processing for an FM Radio-based Passive Coherent Location Radar System[J]. IET Radar Sonar & Navigation, 2012, 6(8):687-696 |
| [3] | Wang H, Wang J, Zhong L. Mismatched Filter for Analogue TV-based Passive Bistatic Radar[J]. IET Radar Sonar & Navigation, 2011, 5(5):573-581 |
| [4] | Poullin D, Flecheux M. Passive 3D Tracking of Low Altitude Targets Using DVB (SFN Broadcasters)[J]. IEEE Aerospace and Electronic Systems Magazine, 2012, 27(11):36-41 |
| [5] | Falcone P, Colone F, Lombardo P. Potentialities and Challenges of WiFi-Based Passive Radar[J]. IEEE Aerospace and Electronic Systems Magazine, 2012, 27(11):15-26 |
| [6] | Weiss A J. On the Accuracy of a Cellular Location System Based on RSS Measurement[J]. IEEE Trans Veh Technol, 2003, 52(6):1 508-1 518 |
| [7] | Rong Peng, Sichitiu M L. Angle of Arrival Localization for Wireless Sensor Networks[C]. Int Conf Sensor and Ad Hoc Communications and Networks, Virginia, USA, 2008 |
| [8] | Wang Ding, Zhang Li, Wu Ying. Constrained Total Last Squares Algorithm for Passive Location Based on Bearing-only Measurements[J]. Science in China(Series F), 2007, 50(4):576-586 |
| [9] | Guvenc I, Chong C C. A Survey on TOA Based Wireless Localization and NLOS Mitigation Techniques[J]. IEEE Commun Surveys & Tutorials, 2009, 11(3):107-124 |
| [10] | Li Wanchun. Studies on Location and Tracking of Passive Radar[D]. Chengdu:University of Electronic Science and Technology of China, 2009(李万春. 外辐射源定位跟踪技术的研究[D]. 成都:电子科技大学, 2009) |
| [11] | Shen Junyang, Molisch A F, Molish S J. Accurate Passive Location Estimation Using TOA Measurements[J]. IEEE Transactions on Wireless Communications, 2012, 11(6):2 182-2 192 |
| [12] | Norouzi Y, Derakhshani M. Joint Time Difference of Arrival/Angle of Arrival Position Finding in Passive Radar[J]. IET Radar Sonar & Navigation, 2009, 3(2):167-176 |
| [13] | Golub H, Charles F. An Analysis of the Total Least Squares Problem[J]. SIAM J Numer Anal, 1980, 17(6):883-893 |
| [14] | Greco M, Stinco P, Gimi F. Cramer-Rao Bounds an Systems[J]. IEEE Trans Aerospace and Electron, 2011, 47(4):2 934-2 948 |
 2015, Vol. 40
2015, Vol. 40


