文章信息
- 范百兴, 李广云, 李佩臻, 易旺民, 杨再华, 杨振
- FAN Baixing, LI Guangyun, LI Peizhen, YI Wangmin, YANG Zaihua, YANG Zhen
- 利用激光干涉测距三维网的加权秩亏自由网平差
- Adjustment of a Laser Interferometer 3D Rank-defect Free-network
- 武汉大学学报·信息科学版, 2015, 40(2): 222-226
- Geomatics and Information Science of Wuhan University, 2015, 40(2): 222-226
- http://dx.doi.org/10.13203/j.whugis20130115
-
文章历史
- 收稿日期:2013-05-09
2. 河南省基础地理信息中心, 河南 郑州, 45000;
3. 北京卫星环境工程研究所, 北京, 100094
2. Henan Province Basic Geographic Information Center, Zhengzhou 450003, China;
3. Beijing Satellite Environment Engineering Research Institute, Beijing 100094, China
激光跟踪仪属于精密的工业大尺寸测量仪器,其采用单频激光干涉测距原理,可以精确测量空间距离,并采用极坐标原理得到空间点的三维坐标值,在航空航天、精密工程与工业测量、机械制造与安装等领域有着广泛的应用[1]。但激光跟踪仪的测角精度与全站仪相比,却没有显著提高。以徕卡 AT901型激光跟踪仪为例,其IFM(interferometer)测距精度为±0.5 μm/m,其测角精度为±(15 μm +6 μm/m),标称点位精度为±(15 μm +6 μm/m),由此可见,激光跟踪仪在采用极坐标原理进行定位时,测角误差是影响点位误差的主要因素[2]。
基于激光跟踪仪极坐标测量已经很难进一步提高点位精度的现状,本文只采用激光跟踪仪的激光干涉距离观测值组成空间三维测边网进行整网平差,消除激光跟踪仪测角误差的影响。在保证足够距离观测值的前提下,基于激光干涉测距的空间三维网在平差解算时存在数亏问题,但与传统秩亏网相比,激光干涉测距的三维空间网是在激光跟踪仪不整平状态下测量的,不存在水平面基准。本文采用加权秩亏自由网平差模型,很好地解决了激光干涉三维测边网的平差问题,将点位精度提高了约3倍。
1 激光干涉三维测边网基准确定
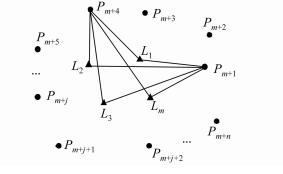
设激光跟踪仪在第 i(i=1,2,…,m)个测站对n个定向点进行了距离观测,同时可以得到n个点的距离值和角度值,如图 1所示。
|
| 图 1 激光跟踪仪空间三维测边网 Fig. 1 Spatial 3D Trilateration Network of Laser Tracker |
设第i个测站对第j个点的距离观测值为Sij,测站坐标为xi,yi,zi ,i=1,…,m,定向点坐标为xj,yj,zj ,j=m+1,…,m+n,则第i个测站对第j个定向点的测量方程为:
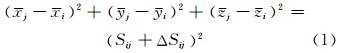
对式(1)求全微分,可得到误差方程为:

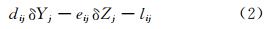
式中,

其中,Xi0,Yi0,Zi0 为测站点的近似坐标; Xj0,Yj0,Zj0 为定向点的近似坐标;Sij0为i、j两点近似坐标计算的斜距值,
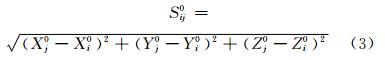
由于角度值不参与平差解算,因此m个测站仅求解测站中心点的三维坐标 Xi0,Yi0,Zi0 ,而不求解测站坐标系的旋转参数 Rx,Ry,Rz 和坐标系尺度因子k,则m个测站依次对n个定向点进行观测时,未知参数的个数为3 m+n ,激光干涉测距所组成的观测方程的个数为m×n,为了使控制网不存在数亏,则需要观测方程个数大于未知参数个数,即满足如下条件:
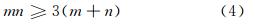
进一步可得:
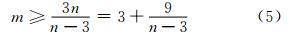
由于m、n均为正整数,因此测站数m≥4,定向点数n≥4,则m、n对应的最小取值如下:m=12、8、6、6、5、5、5、5、4;n=4、5、6、7、8、9、10、11、12。
将式(2)写成矩阵形式为:
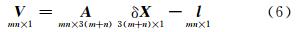
式中,

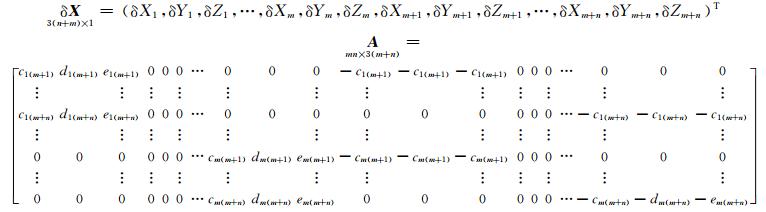
空间三维控制网在进行平差时,为防止控制网系数矩阵出现数亏,需要有足够的起算基准,但该类控制网只有长度而无位置和方位信息,整个控制网的尺度基准根据激光干涉的精密距离观测值确定,因此,系数矩阵 A 为列降秩矩阵,由此导致 N = A T PA 为奇异阵,因此该方程的解不唯一。为了获得唯一解,必须加入新的约束矩阵 G 。附加约束法的秩亏网平差模型如下[3, 4]:

基于激光干涉测距的三维空间网的基准个数d=6,通常,对系数矩阵 G 做如下要求:
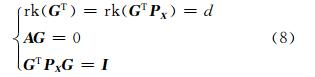
对式(7)按照式(9)进行求解:

按最小二乘原理进行求解,可得:
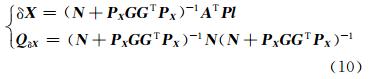
式中,N = A T PA ; P 为观测值权阵。由于各条边的测量可以认为是独立观测,则权阵为对角阵,单位权中误差按式(11)计算:
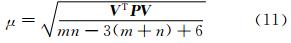
则平差后,未知参数的精度为:
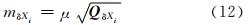
在激光干涉测距三维网中,由于尺度因子已经确定,其所对应的附加矩阵按照式(13)确定:

在激光干涉测距三维网平差中,可以认为各个距离观测值相互独立,观测值的误差主要和测量距离相关,因此需要进行加权平差,本文按照距离先验观测误差±0.5 μm/m确定观测权阵[5]。
3 激光干涉三维测边网概算
在进行秩亏网平差之前,需要求解所有未知参数的近似值,在激光干涉三维测边网中,位置参数分为测站点和定向点两种,按照如下原则进行概算。
在激光跟踪仪测站1坐标系下,激光跟踪仪对 第j个定向点的观测值为 Hz1j,V1j,S1j ,如图 2所示。

|
| 图 2 激光跟踪仪第一测站定位原理 Fig. 2 Polar Coordinate Method of First Laser Tracker Station |
设激光跟踪仪的中心坐标为O(0,0,0),则可以得到第j个定向点在激光跟踪仪测站1坐标系 下的坐标为[6]:

则以 Xj0,Yj0,Zj0 为第j个定向点的近似值。由于定向点坐标的近似值是在测站1坐标系下概算得到的,若第i个测站对第j个定向点的距离观测值为Sij,即可得到如下方程[7]:
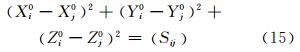
若第i(i >1)个测站对三个以上的定向点进行测量,则该测站点坐标的近似值即可按照式(15)进行测站点坐标的概算,即距离后方交会。
4 附加约束矩阵的中心化和标准化
在激光干涉测距的三维测边网进行秩亏自由网平差时,为满足附加约束矩阵 G T进行标准化的要求,应该首先进行中心化,即把坐标系的原点移到重心点处,然后依此为基准求出三维测边网中每个点的重心坐标,即在 G T矩阵中,应该将近似坐标 xi0,yi0,zi0 改变为重心坐标(xi0-x0,yi0-y0,zi0-z0),从而完成矩阵的中心化[8, 9]。
附加约束矩阵 G T的标准化是在中心化的基础上进行的,根据基准条件可知,G T G 矩阵为一个对角矩阵,为了实现 G 矩阵的标准化,引入辅助矩阵 D :

式中,(xi0,yi0,zi0)即为重心坐标(xi0-x0,yi0- y0,zi0- z0)。 令

将 GT作为秩亏自由网平差的附加约束矩阵,则可以得到:

由此可见,GT矩阵即实现了标准化,并满足式(8)的要求,因此,在激光干涉测距的三维测边网平差中,重心基准不变,其他各个平差值是相对于重心的,所以激光干涉测距的三维测边网平差是以近似值系统为基准的。由于激光干涉测距的三维测边网平差前和平差后基准的形式保持不变,因此,三维测边网属于固定形式的基准,即强基准[10]。
可以证明[3],基于激光干涉测距的秩亏自由网平差后重心坐标等于平差前各点近似坐标的中心坐标,重心点至各点的边长的平方与平差后的方位角乘积之和与平差前和平差后重心点到各点的边长平方和相等。
5 数据解算
为了验证上述模型并测试系统的精度,采用徕卡 AT901-B型激光跟踪仪在某实验室内共布设了L1~L88个测站,测站之间的最大高差约为0.4 m,激光跟踪仪各个测站近似水平[11]。在每个激光跟踪仪测站上对13个定向点进行测量,定向点基本均匀分布在实验场内,定向点之间的最大高差约为1.5 m,其中P1~P8位于地面上,其他点位于墙壁上,点位平面分布如图 3所示。

|
| 图 3 测站点和定向点平面分布图 Fig. 3 Sketch of Station and Orientation Points |
该实验中,观测方程总数为104个,未知参数 个数为63个,基准个数为6个,多余观测个数为47个。采用基于激光干涉测距的秩亏自由网平差模型对三维控制网进行平差解算,平差基准仍旧采用重心基准。平差后,单位权中误差为4.6 μm,均方根误差为7.2 μm,8个测站和13个定向点的平差结果分别如表 1和表 2所示。
| 测站 | X/mm | Y/mm | Z/mm | mX/μm | mY/μm | mXY/μm | mZ/μm | mP/μm |
| 1 | -4 012.571 4 | 616.790 8 | 485.934 | 5.4 | 4.9 | 7.3 | 16.8 | 18.4 |
| 2 | -2 122.129 3 | 2 188.995 2 | 468.5979 | 3.0 | 3.5 | 4.6 | 9.3 | 10.4 |
| 3 | 288.336 6 | -412.545 5 | 420.943 9 | 3.4 | 3.1 | 4.6 | 10.6 | 11.5 |
| 4 | 865.686 6 | -2 406.862 4 | 395.773 1 | 4.5 | 4.9 | 6.7 | 14.8 | 16.2 |
| 5 | -407.509 1 | -243.945 6 | 1 026.473 2 | 2.4 | 2.4 | 3.4 | 6.6 | 7.4 |
| 6 | -2 009.144 6 | 256.478 1 | 1 062.924 7 | 2.9 | 2.8 | 4.0 | 7.1 | 8.2 |
| 7 | 6 122.994 7 | -153.168 8 | 449.104 5 | 2.4 | 4.2 | 4.8 | 10.0 | 11.2 |
| 8 | 4 516.527 2 | -2 401.643 8 | 335.548 3 | 2.7 | 5.1 | 5.8 | 8.2 | 10.0 |
| 测站 | X/mm | Y/mm | Z/mm | mX/μm | mY/μm | mXY/μm | mZ/μm | mP/μm |
| P1 | 2 905.712 0 | -3 246.194 0 | -1 035.153 2 | 3.9 | 8.5 | 9.4 | 13.8 | 16.7 |
| P2 | 4 468.898 2 | -738.757 0 | -1 044.505 9 | 3.3 | 5.3 | 6.2 | 6.3 | 8.9 |
| P3 | 2 283.147 6 | 1 335.689 4 | -989.785 6 | 3.5 | 5.9 | 6.9 | 9.7 | 11.9 |
| P4 | 522.654 2 | 3 148.5701 | -942.736 0 | 4.2 | 6.8 | 8.0 | 13.7 | 15.8 |
| P5 | -1 324.558 4 | 3 592.695 4 | -910.326 3 | 4.2 | 6.8 | 8.0 | 12.8 | 15.1 |
| P6 | -3 766.272 8 | 2 994.268 3 | -877.578 2 | 4.9 | 8.1 | 9.5 | 12.4 | 15.6 |
| P7 | 3 197.078 2 | -619.766 1 | -975.645 0 | 3.1 | 5.3 | 6.1 | 5.6 | 8.3 |
| P8 | 2 431.447 0 | -1 846.769 3 | -973.047 4 | 3.3 | 6.5 | 7.3 | 6.4 | 9.7 |
| P9 | -4 551.276 6 | 3 075.644 8 | 329.445 2 | 3.6 | 5.2 | 6.3 | 26.1 | 26.9 |
| P10 | -5 310.893 6 | 1 831.486 7 | 888.984 5 | 3.2 | 6.5 | 7.2 | 20.1 | 21.4 |
| P11 | -2 649.347 8 | -1 527.199 4 | 693.562 2 | 2.6 | 3.4 | 4.3 | 19.1 | 19.5 |
| P12 | -2 034.486 0 | -1 885.491 9 | 687.770 9 | 2.6 | 3.3 | 4.2 | 19.0 | 19.5 |
| P13 | 585.707 3 | -3 558.274 9 | 503.715 0 | 3.4 | 2.8 | 4.4 | 24.6 | 25.0 |
从表 1和表 2中可以看出,基于激光干涉测距的空间三维网经过秩亏自由网平差后,在12 m×12 m的测量范围内,激光跟踪仪的测站点位误差最大值为18.5 μm,最小值为8.6 μm,点位平均误差为13.6 μm,而定向点的最大点位误差最大值为26.9 μm,最小值为8.3 μm,点位平均误差为16.5 μm,可见,测站点的精度略高于定向点。
从整网的平差情况来看,点位的平面误差mXY的平均值为6.1 μm,垂向误差mZ的平均值为13.0 μm,即点位的平面精度高于垂向精度。此外,由于点 P1~P8布设在稳定的地面上,其垂直于地面的Z向误差明显小于布设在墙壁上的点P9~P13的误差,表明墙壁上的布设点在Z向的稳定性较差。
进一步,将表 2中的测站点和表3中的定向点坐标分量求代数和,分别为2.5×10-12、1×10-4、2×10-4,即点坐标的平差结果满足代数和为零的特点。
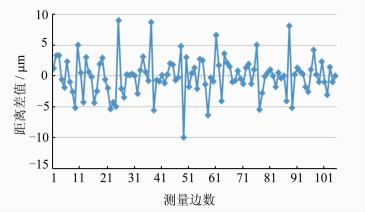
平差后,根据测站点和定向点坐标可以反算得到测站点和定向点的距离,该距离和激光跟踪仪的干涉距离观测值之差可以反映系统的点位平差精度,平差后的解算距离与观测距离差值如图 4所示。
|
| 图 4 平差后解算距离与观测距离差值 Fig. 4 Differential Distance Between Solution Values of Adjusted Point Coordinates and Measurement Values |
从图 4中可以看出,基于激光干涉测距的空间三维网经过秩亏自由网平差后,点坐标反算距离与观测距离差值的最大值为9.0 μm,最小值为-10.0 μm,差值的平均值为-0.07 μm。
6 结 语
采用加权秩亏自由网平差模型很好地解决了基于激光跟踪仪的激光干涉三维测距网的测站点和定向点的平差解算问题,该模型由于消除了激光跟踪仪测角误差的影响,充分利用了激光干涉距离观测值高精度的优势,极大地提高了点位精度。
1) 基于激光干涉测距的空间三维秩亏自由网平差模型,在12 m×12 m测量范围内,将激光跟踪仪的点位精度由87 μm(标称值)提高到了27 μm,大幅度提高了点位精度,可以作为激光跟踪仪、数字摄影测量、经纬仪交会测量等精密大尺寸工业测量的坐标基准。
2) 受实验条件限制,测站点和定向点在垂直方向的图形分布条件较差,尤其是激光跟踪仪测站点之间的垂向最大高差只有0.5 m,导致点位的垂向误差大于平面误差,可以通过改变测站点和定向点在垂直空间内的分布图形,提高点位垂直方向的精度。
3) 影响激光干涉测距三维网点位精度的误差因素主要包括激光跟踪仪的测距误差、球棱镜误差、靶座误差、空间图形分布、实验场地稳定性等,就本次实验条件来看,激光跟踪仪测站点的点位误差小于定向点的点位误差。
4) 根据平差后的测站坐标和定向点坐标,可以反算得到各个测站点到定向点的距离值,其与观测距离差值优于±10.0 μm。
| [1] | Li Guangyun, Li Zongchun. The Principle and Application of Industry Measurement System[M]. Beijing:Surveying and Mapping Press, 2011(李广云, 李宗春. 工业测量系统原理与应用[M].北京:测绘出版社, 2011) |
| [2] | Zhou Weihu. Research on the Precision Theory of Large-Scale Coordinate Measuring Systems[D]. Hefei:Hefei University of Technology, 2000(周维虎.大尺寸空间坐标测量系统精度理论若干问题的研究[D].安徽:合肥工业大学, 2000) |
| [3] | Huang Weibin. The Principle and Application of Modern Adjustment[M]. Beijing:PLA Press, 1992(黄维彬.近代平差理论及其应用[M]. 北京:解放军出版社, 1992) |
| [4] | Song Lijie. The Programming Design of Adjustment[M]. Changsha:National Defense Industry Press, 2009(宋力杰.测量平差程序设计[M].长沙:国防工业出版社, 2009) |
| [5] | Luo Tao, Dong Lan. The Rigorous Adjustment and Its Software Realization of Three Dimensions Control Network Based on Laser Tracker[J]. Journal of Beijing Surveying, 2011(1):1-7(罗涛, 董岚.基于激光跟踪仪三维控制网严密平差与软件实现[J].北京测绘, 2011(1):1-7) |
| [6] | Leica Geosystems.Tracker Programming Interface of emScon 3.5 Programmers[C]. Leica Geosystems AG, Unterentfelden Switzerland, 2010 |
| [7] | Yu Chenghao. Horizontal Precision Estimation of Large-Scale Three-dimensional Control Network[J]. Journal of Surveying and Mapping Science, 2008, 33(2):42-44(于成浩. 大尺寸激光跟踪仪三维控制网平面精度研究[J].测绘科学, 2008, 33(2):42-44) |
| [8] | Shi Yimin. The Characteristics of Defect Free-network Adjustment and the Significance of Robust Datum[J]. Journal of Tongji University, 1991, 19(3):279-286(施一民.论秩亏自由网平差的性质及稳健基准的意义[J].同济大学学报, 1991, 19(3):279-286) |
| [9] | Zhao Chaoying, Huang Guanwen. The General Solution of Defect Free-network Adjustment[J]. Journal of Earth Science and Environmental, 2010, 32(2):215-217(赵超英, 黄观文.秩亏自由网平差及其通解[J].地球科学与环境学报, 2010, 32(2):215-217) |
| [10] | Liu Taosheng, Huang Shengxiang. The Horizontal Coordinate System Transformation Based on Center of Gravity Datum[J]. Journal of Geodetic Surveying and Geodynamics, 2011, 31(2):102-105(刘陶胜, 黄声享. 基于重心基准的平面坐标转换研究[J].大地测量与地球动力学, 2011, 31(2):102-105) |
| [11] | The American Society of Mechanical Engineers. ASME B89.4.19-2006(Performance Evaluation of Laser-Based Spherical Coordinate Measurement Systems)[S]. New York:The American Society of Mechanical Engineers, 2006 |
 2015, Vol. 40
2015, Vol. 40


