文章信息
- 刘炎炎, 叶世榕, 江鹏, 陈昊, 黄志华, 杜仲进
- LIU Yanyan, YE Shirong, JIANG Peng, CHEN Hao, HUANG Zhihua, DU Zhongjin
- 基于北斗三频的短基线单历元模糊度固定
- Instantaneous Ambiguity Resolution of Short Baselines Using BeiDou Triple Frequency Observations
- 武汉大学学报·信息科学版, 2015, 40(2): 209-213
- Geomatics and Information Science of Wuhan University, 2015, 40(2): 209-213
- http://dx.doi.org/10.13203/j.whugis20120200
-
文章历史
- 收稿日期:2013-03-25
2. 中国航天科工集团第九总体设计部, 湖北 武汉 430040;
3. 中国市政工程中南设计研究总院有限公司, 湖北 武汉 430010;
4. 福建省测绘院, 福建 福州 350003
2. The Ninth Department of Overall Design Chinese Aerospace Science and Industry Group, Wuhan 430040, China;
3. Central and Southern China Municipal Engineering Design & Research Institute Co., Ltd., Wuhan 430010, China;
4. Fujian Surveying and Mapping Institute, Fuzhou 350003, China
整周模糊度的快速固定是实现高精度实时定位的关键,是GNSS研究领域的热点问题之一。由于单历元的相位观测方程无法同时求解模糊度参数和位置参数,因此必须引入伪距观测值才能求解。此外,由于短时间内卫星方向的余弦变化很小,观测值是强相关的,导致初始模糊度的解算精度取决于伪距解算精度。而伪距精度有限,导致模糊度的解算精度很差,对应的搜索空间很大,难以搜索到正确的模糊度组[1]。北斗导航定位系统提供了三频的观测值,可以组成波长更长的组合观测值,更有利于模糊度的固定。目前,多频模糊度固定以TCAR和CIR为代表的方法都是采用无几何模型进行模糊度固定的。由于各个卫星的模糊度是各自独立求解的,没有综合利用所有卫星的观测值,因此受多路径等误差干扰严重的卫星模糊度的固定容易出错。Teunissen等[2]对TCAR、CIR、LAMBDA方法进行了比较,指出TCAR 和CIR方法是针对无几何模型设计的,而LAMBDA方法更适合于同时求解位置参数和模糊度参数的有几何模型的模糊度固定。本文基于有几何模型,通过LAMBDA方法逐级固定模糊度。首先在伪距辅助下采用LAMBDA方法固定超宽巷组合模糊度,由于其波长达到4.8 m,可以非常容易固定;然后使用无模糊度的超宽巷相位观测值辅助第一、第二频率宽巷(WL12)和第一、第五频率宽巷(WL15)模糊度的求解,由于超宽巷观测值具有较高的精度,以及WL12、WL15组合观测值的波长为0.8 m左右,通过LAMBDA方法可以非常容易固定WL12、WL15的模糊度;最后使用无模糊度的WL12、WL15代替伪距约束无电离层组合的窄巷模糊度进行求解。
1 模糊度解算制约因素及三频优势 1.1 模糊度固定制约因素
Teunissen[1]指出,快速固定模糊度的关键在于能否将模糊度搜索空间压缩到少数几个备选组合,从而提高搜索成功率,加速模糊度的固定过程。模糊度搜索空间的大小由其浮点解的方差-协方差矩阵决定,可以表示为:

式中,V表示模糊度搜索空间大小;σP表示伪距或无模糊度观测值的精度;n表示观测值历元个数;λ表示相位观测值波长;∝表示正比例关系。
由式(1)可知,要想在有限历元内快速固定模糊度,可以通过提高伪距精度或采用波长更长的组合相位观测值来实现。北斗导航系统提供了三频观测值,可以组成多种长波长的组合观测值,为模糊度的快速固定提供了有利条件。
1.2 北斗三频观测值及其线性组合北斗三频信号特性如表 1所示(北斗官网)。
| 频段 | 频率/Hz | 波长/m |
| B1 | 1 561 098 000 | 0.192 |
| B2 | 1 207 140 000 | 0.248 |
| B5 | 1 268 520 000 | 0.236 |
根据组合观测值定义,可以写出如下三频组合观测值的表达式为[3]:
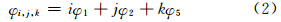
式中,φ1、φ2、φ5是以周为单位的相位观测值;i、j、k表示组合系数。组合观测值对应的频率、波长、模糊度分别为:
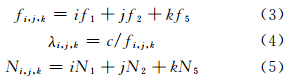
式中,f表示载波频率;λ表示载波波长;c表示真空中的光速;N表示载波模糊度。
假设三个频率相位观测值的噪声均为δ0(cycle),那么组合观测值对应的噪声为:
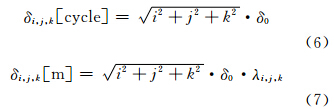
为了能快速求解模糊度,组合观测值应该具有更长的波长、更小的噪声。常用的组合观测值特性如表 2所示。 表 2中,φ0,1,-1由于具有4.8 m的长波长,亦成为超宽巷组合;φ1,-1,0、φ1,0,-1分别称为第一、第二频率宽巷(LW12)和第一、第五频率宽巷(LW15);φ1,1,0、φ1,0,1分别称为第一、第二频率窄巷 (LN12)和第一、第五频率窄巷(LN15)。由于目前接收机载波相位的跟踪精度已经达到0.01 cycle[4],以上三种组合观测值噪声均在cm级,相比其4.8 m、0.84 m、1.02 m的波长,可以忽略其对模糊度固定的影响。
| φi,j,k | 波长/m | 噪声/cycle | 噪声/m |
| φ1,0,0 | 0.19 | δ0 | 0.19δ0 |
| φ0,1,0 | 0.24 | δ0 | 0.24δ0 |
| φ0,0,1 | 0.23 | δ0 | 0.23δ0 |
| φ0,1,-1 | 4.88 | 1.41δ0 | 6.90δ0 |
| φ1,-1,0 | 0.84 | 1.41δ0 | 1.19δ0 |
| φ1,0,-1 | 1.02 | 1.41δ0 | 1.44δ0 |
| φ1,1,0 | 0.10 | 1.41δ0 | 0.15δ0 |
| φ1,0,1 | 0.10 | 1.41δ0 | 0.15δ0 |
卫星钟差和接收机钟差能在双差的过程中完全消除;轨道误差经双差处理后,对短基线(<20 km)的基线影响可以忽略不计。双差对流层延迟误差经过模型改正后也可忽略不计,但是电离层延迟残差的影响却不可忽略,最大可以达到10 cm[5]。因此,对超宽巷观测值 φ0,1,-1以及两个宽巷观测值φ1,-1,0、φ1,0,-1模糊度求解,由于波长较长,可以忽略各种残余误差的影响,而对原始L1、L2、L5的模糊度求解不可忽略电离层的影响。为了充分利用三频观测值,本文融合使用L1、L2频率无电离层组合和L1、L5频率无电离层组合进行基线解算,两个无电离层组合给予相等权比。
本文采用有几何模型进行模糊度解算,同时估计坐标参数和模糊度参数,使用LAMBDA方法逐级进行模糊度固定。使用有几何模型能综合利用所有卫星的伪距或无模糊度相位观测信息,对单一卫星多路径等误差的抗差性更强,可以提高模糊度固定的可靠性[6]。
2.1 固定超宽巷模糊度假设两个接收机h、k同步观测卫星p、q,那么可以得到双差无电离层组合伪距,双差超宽巷观测方程如下:

式中,PC表示无电离层组合伪距观测值;l、m、n分别表示卫星方向余弦;X、Y、Z表示WGS84坐标系下的基线分量;λ表示组合观测值波长;N表示相位整周模糊度参数;ε表示未模型化的各种误差。
假设伪距噪声为0.5 m,由于超宽巷具有4.8 m的长波长,超宽巷模糊度浮点解可以准确求解,甚至直接取整即可达到99%的固定成功率[4]。采用有几何模型,可以得到更可靠的固定成功结果[6]。
2.2 固定宽巷模糊度使用§2.1中模糊度固定的超宽巷观测值代替伪距,约束两个宽巷观测值进行模糊度求解。观测方程如下:
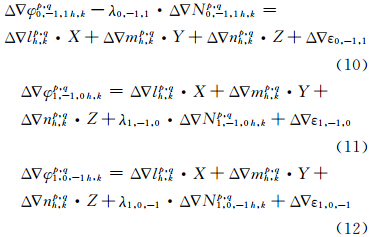
式中,各个符号的含义与式(8)、式(9)相同。
将固定了的模糊度移到观测方程左边,表示与相位观测值合并。超宽巷观测值噪声大约为6 cm,而两个宽巷观测值波长分别长达0.84 m、1.02 m,使用无模糊度的超宽巷观测值可以将宽巷模糊度的搜索空间压缩到少数几种组合,使用LAMBDA方法可以准确搜索出正确的模糊度组。
2.3 固定窄巷模糊度利用模糊度固定的宽巷观测值代替伪距约束无电离层组合相位观测值进行窄巷模糊度求解。为了充分利用三个频率观测值,这里使用L1、L2频率和L1、L5频率的两个无电离层组合进行解算。观测方程如下:

式中,if12、if15分别表示第一、第二频率无电离层组合和第一、第五频率无电离层组合,其余符号与式(8)、式(9)相同。
值得注意的是,由式(15)、式(16)可以看出,经过模糊度分解后,两个无电离层组合LC12、LC15对应一个公共的窄巷模糊度,能充分融合两个无电离层组合观测值进行搜索。同时,在依次固定了LC12、LC15无电离层组合的宽巷、窄巷模糊度后,就可以同时使用这两个无电离层组合进行高精度基线解算。
3 实验验证
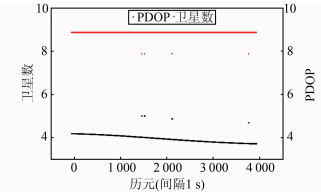
本文采用两台Trimble Net R9多模多频接收机采集了武汉大学到长江水利委员会的一条长13.3 km的基线。卫星截止高度角设为8°,数据采样间隔为1 s,数据长度为1.1 h。图 1给出了两个测站共视卫星的个数以及对应的DOP值。从图 1可以看出,除了少数历元,整个观测时段卫星都有9颗,DOP值在4左右。北斗系统采用CGCS2000坐标框架,GPS采用WGS84框架,两个参考框架之间的差异只有几cm,这对十几km的短基线的影响在mm级以下,可以忽略。使用Bernese软件解算的GPS数据时段整体解作为基线真值,用本文算法解算结果与之比较,进行精度分析。
|
| 图 1 卫星数及其PDOP值 Fig. 1 Satellite Numbers and the PDOP Values |
为了验证LW52超宽巷组合进行模糊度求解具有较高的成功率,对所采集的数据进行逐历元超宽巷解算,图 2、图 3分别给出了LAMBDA方法解算的Ratio值以及基线解算误差时间序列。由图 2可以看出,所有历元的Ratio值都在18以上,88%历元的Ratio值都在50以上,50%历元的Ratio值在100以上,模糊度固定具有很高的可靠性。从图 3可以看出,由于超宽巷观测值噪声较大,基线解的噪声也较大,但是所有历元误差都在2 dm以内,对比超宽巷4.8 m的波长,可以判定所有历元的基线解算结果都是正确的。

|
| 图 2 LW52超宽巷Ratio值 Fig. 2 Ratio of the LW52 Solution |

|
| 图 3 LW52超宽巷基线解算结果 Fig. 3 Position Results of LW52 |
图 4、图 5给出了在超宽巷约束下单历元LW12、LW15联合解算的结果。由图 4可以看出,由于宽巷LW12、LW15的波长分别是0.8 m、1 m,在高精度的超宽巷观测值约束下,宽巷模糊 度解算的可靠性更高,所有历元的Ratio值均在50以上,97%以上历元的Ratio值都在100以上。同时由于宽巷噪声较小,对应基线解的精度也更高,解算误差均在5 cm以内,每个历元的模糊度均得以正确固定。

|
| 图 4 LW12+LW15 解算Ratio值 Fig. 4 Ratio of the LW12+LW15 Solution |

|
| 图 5 LW12+LW15基线解算结果 Fig. 5 Position Results of LW12+LW15 |
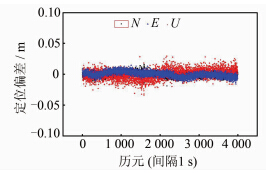
图 6给出了窄巷模糊度LAMBDA解算的Ratio值。由图 6中可以看出,由于窄巷模糊度的波长只有10 cm,Ratio值相比宽巷和超宽巷较小,然而除了其中5个历元的Ratio值在2.5左右,所有历元的Ratio值均在3以上,75%以上历元的Ratio值均在10以上。由图 7可以看出,所有历元基线解算的误差均在5 cm以内,所有历元的窄巷模糊度均可以正确固定。

|
| 图 6 LC12+LC15窄巷模糊度解算Ratio值 Fig. 6 Ratio of the LC12+LC15 Solution |
|
| 图 7 无电离层组合基线解算结果 Fig. 7 Position Results of LC12+LC15 |
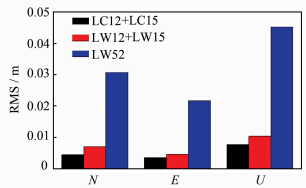
图 8给出了三种解算策略逐历元解算结果的精度统计。由图 8可以看出,超宽巷组合的噪声较大,平面解算精度是3.4 cm,高程精度是5 cm;使用两个宽巷,E、N、U方向的精度都可以达到1 cm;LC组合精度比宽巷提高30%,三个方向均在1 cm以内。
|
| 图 8 三种组合基线解算精度统计 Fig. 8 Position RMS Error of Three Solution Strategies |
使用多频观测值可以组成更多噪声较小、波长较长的组合观测值,更有利于模糊度的固定。本文提出了一种基于有几何模型的逐级模糊度固定方法。首先在伪距辅助下固定超宽巷模糊度,然后用无模糊度的超宽巷约束两个宽巷模糊度求解,最后使用无模糊度的宽巷观测值约束窄巷模糊度求解。采用一条长13 km基线的北斗实测数据表明,基于本文数据的单历元模糊度固定,每一步都可以达到100%的成功率。
| [1] | Teunissen P J G. The Least Squares Ambiguity Decorrelation Adjustment:A Method for Fast GPS Integer Estimation[J]. J Geod, 1995, 70:65-82 |
| [2] | Teunissen P, Joosten P. A Comparison of TCAR, CIR and LAMBDA GNSS Ambiguity Resolution[C]. ION GPS 2002, Portland, Oregon, 2002 |
| [3] | Han S, Rizos C. The Impact of Two Additional Civilian GPS Frequencies on Ambiguity Resolutions Strategies[C]. ION Annual Technical Meeting, Cambridge, MA, 1999 |
| [4] | Montenbruck O, Hauschild A, Steigenberger P, et al. Initial Assessment of the COMPASS/BeiDou-2 Regional Navigation Satellite System[J]. GPS Solutions, 2013, 17(2):211-222 |
| [5] | Feng Y M. GNSS Three Carrier Ambiguity Resolution Using Ionosphere-Reduced Virtual Signals[J]. J Geod, 2008, 82:847-862 |
| [6] | Vollath U, Birnbach S, Landau H. Analysis of Three Carrier Ambiguity Resolution (TCAR) Technique for Precise Relative Positioning in GNSS-2[C]. ION GPS, Toulouse, France, 1998 |
 2015, Vol. 40
2015, Vol. 40



