文章信息
- 朱锋, 张小红
- ZHU Feng, ZHANG Xiaohong
- 滤波降阶和等效性操作的捷联惯导静基座精对准
- Fine Alignment of SINS on Stationary Base Using a Reduced-order Filter and Equivalence Operation
- 武汉大学学报·信息科学版, 2015, 40(2): 204-208
- Geomatics and Information Science of Wuhan University, 2015, 40(2): 204-208
- http://dx.doi.org/10.13203/j.whugis20130461
-
文章历史
- 收稿日期:2013-09-03
捷联惯导初始对准是惯性导航和组合导航的关键技术之一,它为系统提供精准的初始姿态信息,无论在航天航空导航、武器弹药制导,还是在地面车辆、船舰运行,都要求初始对准具有准确性和快速性[1]。对于一般的组合导航系统,在进入正式导航工作状态前,需要进行10~20 min的静基座对准[2],包括粗对准和精对准,以获取精确的初始姿态信息,为加速度计提供高精度的测量方位基准。目前,静基座下的精对准方法研究主要集中在以下几个方面:①对准方法研究[3, 4, 5];②误差模型研究[6, 7, 8, 9, 10, 11];③估计方法研究[1];④可观测性分析[12, 13]。总体来说,静基座下的精对准已相对成熟,对于高精度惯导,通常采用零速条件下的Kalman滤波自对准,对于低精度惯导,由于陀螺漂移和噪声大,不能准确测得地球自转角速度,对于陀螺零偏超过5 o/h的惯导系统,根本不具备自对准能力[14],通常需要GPS提供的速度信息来进行航向角计算。
Kalman滤波降阶可以消去不可估计的状态参数,降低系统阶数,简化估计器。Aranda[15]经过误差预算和协方差分析后,直接去除零偏项,提出了降阶的5参数Kalman滤波模型;Lu[16]同样分析了降阶的5参数Kalman滤波模型,并提出了闭环修正方案,讨论了随机模型参数对滤波的影响;严恭敏[17]对比力精对准模型做了降阶处理,结果表明降阶滤波器和全阶滤波器估计精度相当,并且降低了计算量,消除了不可估计状态对滤波器的不利影响;张开东[18]研究了基于捷联惯导的航空矢量重力测量中的降阶滤波算法。这些方法只是删去了不必要的状态量,达到滤波降阶,以简化模型的目的;而对于静基座精对准模型,未从严密的可观测性分析出发来进行滤波降阶,并且缺乏机械编排和惯导误差模型的等效性问题的研究,使得匹配不等,导致精对准失 败。本文从严密的滤波降阶和等效性操作原理基础上,提出了改进的简化模型,极大地方便了精对准的实现过程。
1 静基座精对准模型及等效性操作
由比力方程经过误差微扰后,可得到φ角的速度误差方程[7]:

在静基座条件下,Vn=0,则有 平台失准角 φ 往往由于定义不清,导致有不同的误差方程[6, 19],本文定义的 φ 角满足以下方程:
式中,Rb n为真实的方向余弦矩阵; 因静基座下,ω enn=0,ω ien为常数,得δ ω inn=δ ω ien+δ ω enn=0,因此有:
静基座条件下,陀螺和比力误差可以按常数估计[13],这样可得到Kalman估计的状态方程:
相应的量测方程为:
式中,V Mech由机械编排得到; V n为观测噪声。
惯导机械编排和误差方程的误差传播具有等效性。机械编排实质为惯导动力学模型的数值积分解,所有的误差内含在数值积分过程中,随着积分的进行,误差逐步累积,但这种误差由最终的导航解(位置、速度、姿态)来反映;而误差方程实质为误差传播的解析表达式,通过解误差微分方程,在误差初值已知的情况下,可以得到位置、速度、姿态误差的解析值,这种误差与包含在机械编排导航解的误差是相等的,这从松组合Kalman的观测方程也可以看出。误差传播的等效性来源于机械编排与误差方程使用同一套动力学模型,若误差方程做了条件约束,相应的在机械编排中也要体现。在静基座对准中,这种操作尤为重要。式(2)是在 V n=0和位置已知的条件下导出的,原始的动力学模型因条件的约束而改变,此时,机械编排中也要做相应的改变来顾及这两个条件。两者的等效性操作体现如表 1所示。
对于表 1中的第三项等效性操作,事实上,δ V n表示的是量测的速度误差,由于真实速度为 零,因而在数值上δ V = V Mech,从速度误差方程中可以看到,有科氏力项 ω ien×δ V n,而在机械编排中,同样使用 ω ien× V Mech作为科氏力项的计算,保持两者等价,而如果用 V n=0代入,将会导致错误。从误差方程中可以看出,δ V n是由自身误差引起的科氏力、平台失准角和加速度计零偏综合影响引起的,而各项对应机械编排中的则是自身更新的 V Mech计算科氏力;平台失准角内含在初始方向余弦矩阵,由姿态更新传递;加速度计零偏内含在速度增量观测值中,由速度更新来传递,两者达到了等效性操作。
基于以上等效性操作分析,可以同时在速度误差方程中和机械编排中去除科氏力项。速度误差方程如下:
此时的δ V n不是真正意义上的速度误差,它吸收了科氏力的影响,同时在机械编排中,也不需要计算科氏力项 ω ien× V Mech。这样可以简化精对准模型,消除因位置不准确带来的 ω ien计算误差对模型的影响。
2 可观测性分析的滤波降阶
以式(6)和式(7)为Kalman滤波方程进行静基座静对准模型的可观测分析。首先计算4阶可观测性矩阵:
式中,O 4为12阶方阵。经初等变化矩阵 N 左乘后得:
由式(10)可得rank O 4 =rank NO 4 =9,O 4秩亏,因此可观测性矩阵 O 12也秩亏,系统不完全可观测,有三个状态量不可观测。
下面分析不可观测状态量的选取,有表达式:
式中, 由于第一行为观测方程等式,而第四行为零,省去这两行,取中间两行得:
式(13)表明,平台失准角 φ 和零偏可以通过观测值一阶导 将n系下的 G和Ω 表达式代入,可得:
通过t1~t6不能解出所有的 φ 、 a n和 ε n,而精对准的目的在于求得平台失准角 φ ,它不能选为不可观测量,因此有两组不可观测量 aN,aE,εE 和 aN,εN,εE ,利用Kalman滤波得到的方差收敛速度来判断状态量的可观测性度[20],最终可选 aN,aE,εE 为不可观测量。这样在误差状态方程中可以去掉这些状态量,改变相应的状态矩阵 F ,达到滤波降阶的目的。
3 改进后的简化模型
基于以上分析,全阶的静基座精对准模型可做如下改进:①由于垂直通道和水平通道的耦合很小,垂直通道的速度误差估计可以去掉[13](认为等于零);②b系下的零偏及过程噪声转换至n系下,消除 R 的影响;③ aN,aE,εE 为不可观测量,去掉这些状态量;④利用等效性操作,去掉科氏力项 ω ien×δ V n的影响。改进后的简化模型为:
相应的量测方程去掉垂直通道速度,同时在机械编排中的垂直速度设为零,不做更新。对于b系下过程噪声可以转换至n系下证明。以陀螺过程噪声 η εb为例,状态方程(6)中的陀螺过程噪声为:
从以上改进步骤可以看出,状态量减小,使得运行速度加快,将b系下的零偏及过程噪声转换至n系下,使得状态矩阵 F和过程噪声矩阵L成为简单的常矩阵,不需要每步更新计算,最后省去了科氏力项的计算。简化模型不仅简化了精对准实现过程,也减少了相应的运算时间。
4 实验测试
本文通过模拟静基座惯导的初始精对准过程来比较三种模型的估计精度和收敛速度,验证简化模型的有效性。仿真条件如下:P =(34°,75°,100 m),三个姿态角均为零,采样率为1 Hz,时间 长度为10 min,陀螺零偏ε=0.01 °/h,陀螺噪声σε=0.001 °/ 图 1清晰地比较了三种模型的精对准效果。7阶模型在不同的失准角条件下都能稳定收敛,并且具有和10阶模型同样的滤波效果及估计精度,表明本文提出的简化模型是正确的。各失准角条件下,7阶模型的收敛时间均在120 s以内,估计精度的绝对值依次为2.7′、9.8′和40.5′,失准角越大,估计精度越差,但仍能保持在1°以内。而对于12阶模型,在小失准角下和降阶模型具有相同的滤波效果,随着失准角增大,收敛时间变长,但收敛以后同样具有相同的估计精度,这是因为简化模型本质上未改变精对准模型的结构,它们都是一种基于零速条件下的Kalman滤波自对准,其估计的极限精度与仪器零偏和位置有关[21]。而对于东向和北向失准角收敛的情况,三种模型基本一致。
精对准结束以后,通过对机械编排输出的姿态矩阵进行失准角改正后输出的姿态角如表 2所示。
由于本文模拟数据设置的姿态角均为0°,因此表 2中的姿态角可以直接表示为估计精度。从表 2可以看出,各种模型的姿态估计精度相当。失准角越大,估计精度越低。因此当失准角收敛后,如120 s处,对机械编排输出的姿态角进行改正,并且重新初始化静对准模型,新的一轮精对准相当于在较小的失准角小启动,这样可以逐级设置,提高估计精度。
不同条件下的仿真实验表明,本文的结果具有普遍性。从本文看,简化模型不仅使得模型大大简化,减轻了计算负担,加快了运行速度,而且保持了原有的快速收敛性和较高的估计精度,是一种优化的静基座精对准方法。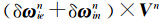 =0,ω enn=0,又因位置已知,不存在误差,因此,δ γ n=0。另外 f n= g n,整理以后,将比力误差表示为零偏和噪声项,即δ f b= a b+ η ab,得:
=0,ω enn=0,又因位置已知,不存在误差,因此,δ γ n=0。另外 f n= g n,整理以后,将比力误差表示为零偏和噪声项,即δ f b= a b+ η ab,得:
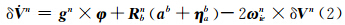

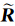 bn为存在平台误差的方向余弦矩阵,两者通过 φ 角相联系,这样得到 φ 角误差模型,其中陀螺误差表示为零偏和噪声项,即
bn为存在平台误差的方向余弦矩阵,两者通过 φ 角相联系,这样得到 φ 角误差模型,其中陀螺误差表示为零偏和噪声项,即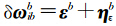 ,得:
,得:
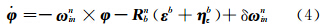
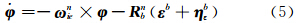


误差方程 机械编排
Vn=0,ωenn=0
位置已知,δγn=0去除科氏力项ωien×δVn姿态、速度误差
不计算ωenn,直接赋零初始位置由真值代入,以后位置不做更新去除科氏力项ωien×VMech姿态、速度更新 
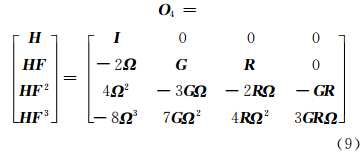



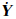 为观测值一阶导,其他类推。将式(11)两边左乘同一个常矩阵,等式右边整理后得:
为观测值一阶导,其他类推。将式(11)两边左乘同一个常矩阵,等式右边整理后得:


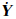 和二阶导
和二阶导 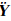 来求解,同时由于 a n= Ra b,ε n= Rε b,表明在误差状态方程(6)中b系下的零偏可以由n系下的等效零偏来替代估计,这样可以消除 R 不准确带来的影响。将式(13)中的第二行两边同乘以-1,零偏由等效零偏来表示,对于等式右边,用 t 来替换,得:
来求解,同时由于 a n= Ra b,ε n= Rε b,表明在误差状态方程(6)中b系下的零偏可以由n系下的等效零偏来替代估计,这样可以消除 R 不准确带来的影响。将式(13)中的第二行两边同乘以-1,零偏由等效零偏来表示,对于等式右边,用 t 来替换,得:


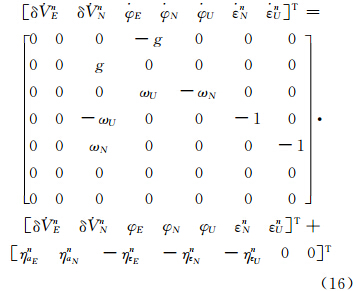

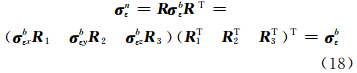
 ,加计零偏a=100 μg,加计噪声σa=10 μg/
,加计零偏a=100 μg,加计噪声σa=10 μg/ 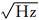 。其中共设了三组失准角:1°、5°和10°。根据状态个数,精对准模型可分为12阶、10 阶和7阶,12阶和10阶模型均未做相应的改进,而7阶模型为改进后的简化模型,使用三种模型对不同失准角状态下的惯导数据实施了精对准。其中天向失准角的滤波收敛结果如图 1所 示。
。其中共设了三组失准角:1°、5°和10°。根据状态个数,精对准模型可分为12阶、10 阶和7阶,12阶和10阶模型均未做相应的改进,而7阶模型为改进后的简化模型,使用三种模型对不同失准角状态下的惯导数据实施了精对准。其中天向失准角的滤波收敛结果如图 1所 示。

图 1 天向失准角的滤波收敛结果
Fig. 1 Filter Convergence of Up Misalignment Angle
失准角1° 失准角5° 失准角10°
航向角 俯仰角 翻滚角 航向角 俯仰角 翻滚角 航向角 俯仰角 翻滚角 7阶
0.045 827
0.014 187
-0.017 084
-0.170 625
0.209 733
-0.232 563
-1.022 61
0.739 549
-0.884 715
10阶
0.047 166
0.014 579
-0.015 390
-0.168 615
0.210 063
-0.230 654
-1.017 84
0.739 037
-0.882 453
12阶
0.047 184
0.014 578
-0.015 387
-0.166 924
0.207 806
-0.232 389
-1.468 77
0.616 231
-0.982 469
| [1] | Qian Weixing. Research on High-Precision Initial Alignment of Strapdown Inertial and Integrated Navigation System[D]. Nanjing:Nanjing University of Aeronautics and Astronautics, 2010(钱伟行. 捷联惯导与组合导航系统高精度初始对准技术研究[D]. 南京:南京航空航天大学, 2010) |
| [2] | Wan Dejun, Fang Jiancheng. Initial Alignment of Inertial Navigation[M]. Nanjing:Southeast University Press, 1998:9-10(万德钧, 房建成. 惯性导航初始对准[M]. 南京:东南大学出版社, 1998:9-10) |
| [3] | Fu Qiangwen, Qin Yongyuan, Zhang Jinhong, et al. Rapid Recursive Least-square Fine Alignment Method for SINS[J]. Journal of Chinese Inertial Technology, 2012, 20(3):278-282(付强文, 秦永元, 张金红, 等. 捷联惯导系统快速最小二乘精对准方法[J]. 中国惯性技术学报, 2012, 20(3):278-282) |
| [4] | Li Yao, Xu Xiaosu, Wu Bingxiang. Gyroscompass Self-alignment of SINS[J]. Journal of Chinese Inertial Technology, 2008, 16(4):386-389(李瑶, 徐晓苏, 吴炳祥. 捷联惯导系统罗经法自对准[J]. 中国惯性技术学报, 2008, 16(4):386-389) |
| [5] | Qin Yongyuan. Inertial Navigation[M].Beijing:Science Press, 2006:361-375(秦永元. 惯性导航[M].北京:科学出版社, 2006:361-375) |
| [6] | Benson D O. A Comparison of Two Approaches to Pure-Inertial and Doppler-Inertial Error Analysis[J]. Aerospace and Electronic Systems, IEEE Transactions on, 1975, 11(4):447-455 |
| [7] | Shin E H. Estimation Techniques for Low-cost Inertial Navigation[D]. Calgary:University of Calgary, 2005 |
| [8] | Scherzinger B, Reid D B. Modified Strapdown Inertial Navigator Error Models[C]. Position Location and Navigation Symposium, Las Vegas, USA, 1994 |
| [9] | Scherzinger B. Inertial Navigator Error Models for Large Heading Uncertainty[C]. Position Location and Navigation Symposium, Atlanta, USA, 1996 |
| [10] | Myeong-Jong Y, Jang-Gyu L, Heung-Won P. Comparison of SDINS In-flight Alignment Using Equivalent Error Models[J]. Aerospace and Electronic Systems, IEEE Transactions on, 1999, 35(3):1 046-1 054 |
| [11] | Godha S. Performance Evaluation of Low Cost MEMS-based IMU Integrated with GPS for Land Vehicle Navigation Application[D]. Calgary:University of Calgary, 2006 |
| [12] | Goshen-Meskin D, Bar-Itzhack I Y. Observability Analysis of Piece-wise Constant Systems with Application to Inertial Navigation[C]. The 29th IEEE Conference on Decision and Control, Hawall, USA, 1990 |
| [13] | Bar-Itzhack I Y, Berman N. Control Theoretic Approach to Inertial Navigation Systems[J]. Journal of Guidance Control Dynamics, 1988, 11(3):237-245 |
| [14] | Groves P D. Principles of GNSS, Inertial, and Multisensor Integrated Navigation Systems[M]. Boston:Artech House, 2008:148-149 |
| [15] | Aranda J, De La Cruz J M, Dormido S, et al. Reduced-order Kalman Filter for Alignment[J]. Cybernetics and Systems:An International Journal, 1994, 25(1):1-16 |
| [16] | Shaolin L, Ling X, Jiabin C. Reduced-order Kalman Filter for RLG SINS Initial Alignment[C]. Control and Decision Conference, Yantai, China, 2008 |
| [17] | Yan Gongmin, Qin Yongyuan. Inertial Alignment Accuracy Analysis and Simulation of Strapdown Inertial Navigation System on a Stationary Base[J]. Computer Simulation, 2006, 23(10):36-40(严恭敏, 秦永元. 捷联惯导系统静基座初始对准精度分析及仿真[J]. 计算机仿真, 2006, 23(10):36-40) |
| [18] | Zhang Kaidong, Wu Meiping, Hu Xiaoping. Reduced Order Filtering Algorithm of Airborne Vector Gravimetry Based on SINS[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(3):204-209(张开东, 吴美平, 胡小平. 基于捷联惯导的航空矢量重力测量的降阶滤波算法[J]. 测绘学报, 2006, 35(3):204-209) |
| [19] | Weinred A, Bar-Itzhack I Y. The Psi-Angle Error Equation in Strapdown Inertial Navigation Systems[J]. Aerospace and Electronic Systems, IEEE Transactions on, 1978, 14(3):539-542 |
| [20] | Jiang C F, De Jun W. A Fast Initial Alignment Method for Strapdown Inertial Navigation System on Stationary Base[J]. Aerospace and Electronic Systems, IEEE Transactions on, 1996, 32(4):1 501-1 504 |
| [21] | Yeon F J, Yu P L. Error Estimation of INS Ground Alignment Through Observability Analysis[J]. Aerospace and Electronic Systems, IEEE Transactions on, 1992, 28(1):92-97 |
 2015, Vol. 40
2015, Vol. 40


