文章信息
- 罗小敏, 蔡昌盛, 朱建军, 潘林, 李施佳
- LUO Xiaomin, CAI Changsheng, ZHU Jianjun, PAN Lin, LI Shijia
- 利用Galileo IOV卫星观测数据的单点定位精度分析
- Accuracy Assessment of Single Point Positioning Based on Observational Data from Galileo IOV Satellites
- 武汉大学学报·信息科学版, 2015, 40(2): 199-203
- Geomatics and Information Science of Wuhan University, 2015, 40(2): 199-203
- http://dx.doi.org/10.13203/j.whugis20130063
-
文章历史
- 收稿日期:2013-04-22
早期Galileo导航与定位方面的研究工作通常是基于模拟数据开展的[1, 2, 3, 4],但模拟数据缺乏一定的真实可靠性。自从Galileo系统的第一颗在轨实验卫星 (GIOVE-A) 于2005年12月成功发射以来,一些学者开始利用实测数据对Galileo的定位性能进行研究[5, 6, 7, 8, 9, 10, 11, 12]。文献[5, 6]基于实时时钟估计系统(real-time clock estimation,RETICLE) 提供的Galileo实时轨道和钟差数据对GPS/Galileo组合定位的性能进行了评估,然而RETICLE系统目前已停止提供Galileo实时产品。文献[7]采用实测的Galileo卫星数据,利用德国慕尼黑工业大学天文和大地测量研究所提供的Galileo卫星精密星历和钟差数据,首次报道了Galileo单系统精密单点定位 (precise point positioning,PPP) 的结果,得出利用GIOVE/IOV观测值的Galileo PPP水平方向精度优于0.45 m,高程方向精度优于0.4 m。由于Galileo系统目前还处于实验阶段,且卫星数量有限,该精度明显低于当前GPS PPP的精度。Galileo系统经过这些年的发展,首次具备了基于4颗IOV卫星的导航定位能力。GPS World第一时间报道了4颗Galileo IOV卫星的定位结果[8, 9, 10, 11, 12],引起了业界普遍关注,然而这些研究工作仅基于少量的IOV卫星观测数据,难以准确地反映当前Galileo星座的定位性能。
本文采用不同全球多卫星导航系统实验网(multi-GNSS experiment,MGEX)跟踪站连续7 d的IOV卫星观测数据和广播星历数据,对单独Galileo和组合GPS/Galileo单点定位(single point positioning,SPP) 进行了精度评估,并与GPS SPP的精度进行了对比分析。
1 MGEX全球监测网
MGEX 由IGS组织在2011年底建立,于2012年2月首次对多GNSS卫星导航信号进行了跟踪并开展试验。MGEX监测站能对GPS、GLONASS、BeiDou、Galileo等多个卫星系统的多频段导航信号进行跟踪和监测,其数据处理中心地壳动力学数据信息系统、德国地图制图和大地测量研究所、德国地学研究中心等机构对卫星的监测信号进行分析和处理后,以RINEX 2.11、3.00、3.01、3.02等格式免费提供给全球用户。目前,全球共有近40个MGEX跟踪站[13, 14]。 截止至本文完成,MGEX跟踪站的近10个测站已提供4颗IOV卫星的广播星历数据,这为开展Galileo导航定位的研究工作提供了有利的条件。
2 Galileo单点定位模型
利用测距码进行伪距测量时,Galileo单点定位的观测方程可表示为:
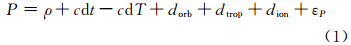
式中,P为Galileo IOV卫星的伪距观测值;ρ为卫星至接收机间的几何距离; c为光速;dt为接收机钟差;dT为卫星钟差;dorb是卫星轨道误差;dtrop是对流层延迟误差;dion是电离层延迟误差;εP是伪距多路径误差及观测噪声。
鉴于Galileo系统采用的NeQuick电离层延迟改正模型属于一种半经验模型[15],本文直接采用双频伪距消电离层组合观测值进行单点定位试算,则观测方程变为:
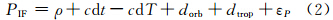
式中,
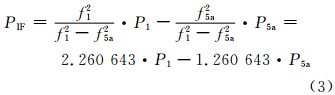
式中,P1、P5a分别为Galileo C1和C5伪距观测值;f1、f5a分别为 Galileo E1和E5a的载波频率。
3 数据处理与结果分析
Galileo单点定位数据处理时,卫星截止高度角设为5°,同时剔除载噪比C/N0<15 dBHz的观测数据。观测方程中,Galileo IOV卫星轨道和卫星钟差的误差通过MGEX跟踪站最新发布的广播星历计算获得。对流层延迟采用Saastamoinen模型改正。另外,顾及卫星钟差相对论改正和地球自转改正。采用最小二乘算法计算测站的三维位置坐标、接收机钟差共4个待估参数。处理结果同IGS-MGEX发布的各测站已知坐标进行比较,计算出位置误差,并转换为测站坐标东(E)、北(N)、上(U)三个方向。
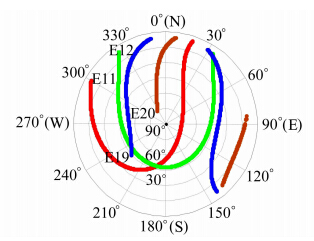
图 1为MGEX跟踪站REUN测站2013-03-21的Galileo IOV卫星的星空图。从图 1可以看出,该站当天能观测到4颗IOV卫星。图 2给出了REUN测站连续7 d采样间隔为30 s的Galileo IOV卫星观测历元数的统计值。图 2表明,各颗IOV卫星7 d平均观测历元数的均值大致相同,分别为1 006、964、957、940。
|
| 图 1 Galileo IOV卫星星空图 (2013-03-21) Fig. 1 Sky Plot of Galileo IOV Satellites(March 21,2013) |

|
| 图 2 Galileo IOV卫星观测历元数(2013-03-21至 2013-03-27) Fig. 2 Numbers of Observation Epochs of Galileo IOV Satellites (March 21,2013-March 27,2013) |
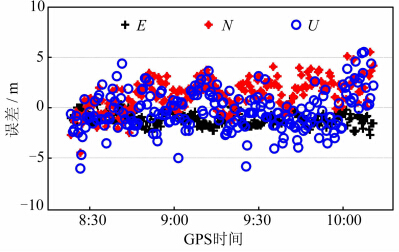
图 3为REUN测站Galileo单点定位单历元最小二乘解的位置误差图,该站在2013-03-21当天的8:23~10:10能同时观测到4颗IOV卫星。从图 3中可以看出,E、N、U三个方向的误差曲线在-6~6 m之间波动,其中U方向的误差曲线波动最大,E方向的误差曲线波动最小。
|
| 图 3 Galileo单点定位位置误差(2013-03-21) Fig. 3 Position Errors of Galileo SPP Solutions(March 21,2013) |
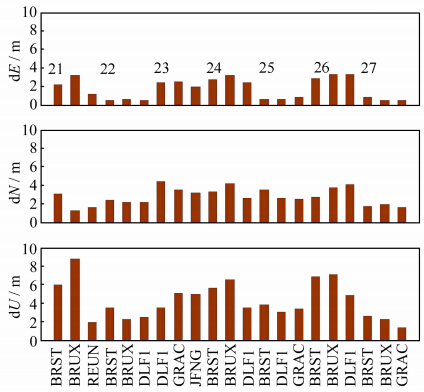
图 4进一步给出了连续7 d不同测站共计21组数据的Galileo单点定位位置误差的RMS (均方根) 统计值。需要说明的是:① 每天任意取3个MGEX跟踪站的观测数据进行试验;② 不同天、不同测站同时观测到4颗IOV卫星的时间区间、时间长短并不一致。从图 4可以看出,整体上,Galileo单点定位水平方向精度优于4.5 m,高程方向精度优于9.0 m。另外,2013年3月21、24及26日这三天的BRUX测站的定位精度较差,经分析,主要是因为这三天该站观测到的4颗IOV卫星的空间几何分布的结构较差,且观测到的时间较短。
|
| 图 4 同测站连续7 d的Galileo单点定位RMS统计(2013-03-21至2013-03-27) Fig. 4 RMS of Galileo SPP Solutions for Different Stations on 7 Consecutive Days(March 21,2013-March 27,2013) |
为了进一步对比分析Galileo SPP的定位性能,本文设计了如下试验方案: ① 基于三维位置精度因子(position dilution of precision,PDOP)最小的4颗GPS卫星单点定位;② 基于全星座GPS卫星单点定位;③ 基于4颗Galileo IOV卫星单点定位;④ 基于4颗GPS卫星+ 4颗Galileo IOV卫星的组合GPS/Galileo单点定位;⑤ 基于全星座GPS+4颗Galileo IOV卫星的组合GPS/Galileo单点定位。
需要说明的是:① 伪距观测值分别来自GPS和Galileo两种不同系统,需要合理地确定这两类观测值的权值。Helmert验后方差分量估计方法被广泛应用于确定不同类观测值的定权,但是该方法要求各类观测值具有足够的多余观测量[16]。目前,Galileo系统仅有4颗IOV卫星,并没有多余观测量。鉴于此,首先设定GPS和Galileo伪距观测值测距误差的标准差,然后利用以卫星高度角为变量的正弦函数模型计算观测值方差的方式定权。本文通过大量的数据试验,给定GPS和Galileo伪距观测值测距误差的标准差都为0.3 m。② 相比于单系统定位,组合GPS/Galileo SPP的待估参数增加了GPS-Galileo系统时间差(GPS-Galileo time offset,GGTO) 参数。
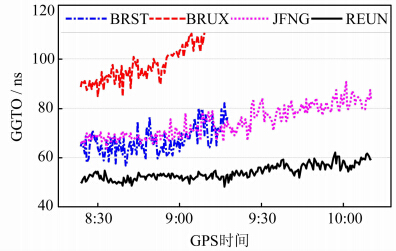
图 5给出了2013年3月21日不同测站的GGTO曲线图,笔者利用最小二乘算法对GGTO参数进行了单历元求解。图 5表明,当天8:23~10:10时间段内,各测站的GGTO存在一定程度的波动,约为20 ns;相比于其他测站,REUN测站的GGTO曲线较平滑,这是因为该站在8:23~10:10时间段有4颗IOV卫星参与解算GGTO,而其他测站仅有1~2颗IOV卫星参与解算。
|
| 图 5 不同测站的GPS-Galileo系统时间差 Fig. 5 GPS-Galileo Time Offset at Different Stations |
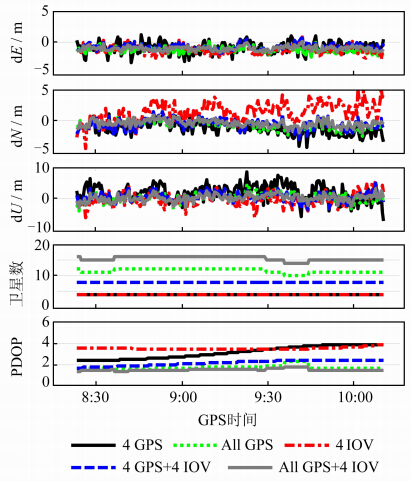
图 6为2013年3月21日REUN测站基于5种不同方案的定位误差图,表 1为5种方案定位结果的统计。从图 6和表 1可以看出,方案①与方案③的定位误差较接近;方案④较方案①、③而言,定位精度有明显提高,RMS(3D)改善率分别有4颗时,增加Galileo卫星后能有效地改善星座的空间几何分布,统计得出方案①、④的PDOP均值分别为3.1、2.1;方案④较方案①而言,PDOP值改善率达32.3%。与方案②对比,方案⑤的定位精度虽有所改善,但改善程度不明显,这说明当GPS卫星数充足时,增加4颗Galileo卫星后对星座的空间几何分布并无明显改善 (见图 6最下面的那个图),其中方案②、⑤的PDOP均值分别为1.7、1.5,PDOP值改善率为11.8%。 为48.3%、33.8%。这是因为当GPS卫星数仅
|
| 图 6 不同方案单点定位的结果(2013-03-21) Fig. 6 Position Results of SPP Solutions for Different Schemes (March 21,2013) |
| 标准差 | RMS | RMS(3D) | |||||
| E | N | U | E | N | U | ||
| 方案① | 0.858 | 0.945 | 2.559 | 1.165 | 1.531 | 3.097 | 3.646 |
| 方案② | 0.432 | 0.636 | 1.474 | 1.225 | 0.959 | 1.514 | 2.171 |
| 方案③ | 0.644 | 1.522 | 1.962 | 1.159 | 1.669 | 1.998 | 2.849 |
| 方案④ | 0.459 | 0.784 | 1.410 | 0.866 | 0.872 | 1.430 | 1.885 |
| 方案⑤ | 0.341 | 0.541 | 1.103 | 1.002 | 0.701 | 1.121 | 1.659 |
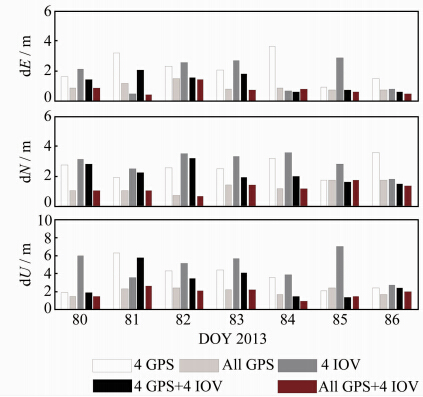
图 7进一步给出了连续7 d BRST测站基于不同方案的定位误差RMS统计值 (因BRST测站2013年3月23日当天无法同时观测到4颗IOV卫星,故选取GRAC测站进行试验)。表 2为图 7中不同方案定位误差的RMS均值统计。由图 7和表 2可知:①当前Galileo的定位性能明显低于基于全星座的GPS定位,其原因是Galileo系统目前仅有4颗IOV卫星,而正常运行的GPS卫星数达31颗。② 整体上分析,相比于GPS单系统,GPS/Galileo组合系统在3个坐标分量上的定位精度均有不同程度的提高。③ 在第81天,增加Galileo卫星的组合系统在N、U方向的定位精度反而有所降低,这主要是受Galileo卫星广播星历精度较低的影响。
|
| 图 7 不同方案连续7天单点定位位置误差的RMS统计(2013-03-21至2013-03-27) Fig. 7 RMS of SPP Position Errors for Different Schemes on 7 Consecutive Days(March 21,2013-March 27,2013) |
| E | N | U | |
| 方案① | 2.180 | 2.575 | 3.543 |
| 方案② | 0.943 | 1.216 | 1.989 |
| 方案③ | 1.737 | 2.909 | 4.832 |
| 方案④ | 1.254 | 2.131 | 2.885 |
| 方案⑤ | 0.795 | 1.155 | 1.776 |
| 方案④相对于方案①的改善率/% | 42.5 | 17.2 | 18.6 |
| 方案⑤相对于方案②的改善率/% | 15.7 | 5.0 | 10.7 |
本文基于MGEX跟踪站不同测站连续7 d的IOV卫星观测数据和广播星历数据,对目前Galileo单点定位的精度进行了评估。结果表明:① 基于4颗IOV卫星的Galileo单点定位的水平方向精度优于4.5 m,高程方向精度优于9.0 m。② 当前Galileo系统的定位性能低于GPS系统,但与仅有4颗GPS卫星的单点定位性能较接近。③ 相比于GPS单系统,GPS/Galileo组合定位在3个坐标分量上的定位精度均有不同程度的提高。随着Galileo卫星数量的增加和系统性能的改善,Galileo定位精度将会得到进一步的提升。
| [1] | Zhao Chunmei, Ou Jikun, Yuan Yunbin. Positioning Accuracy and Reliability of Galileo, Integrated GPS-GALILEO System Based on Single Positioning Model[J]. Chinese Science Bulletin, 2005, 50(12):1 252-1 260 |
| [2] | Shen X, Gao Y. GPS/Galileo PPP, Analyzing the Impacts of Galileo and Modernized GPS on Precise Point Positioning[C]. ION ITM 2006, Monterey, California, USA, 2006 |
| [3] | KjØrsvik N S, Øvstedal O, Gjevestad J G O. Kinematic Precise Point Positioning During Marginal Satellite Availability[C]. 2007 IAG General Assembly, Perugia, Italy, 2007 |
| [4] | Diessongo H T, Schüler T, Junker S. Precise Position Determination Using a Galileo E5 Single-frequency Receiver[J]. GPS Solutions, doi:10.1007/s10291-013-0311-2 |
| [5] | Cao W, Hauschild A, Steigenberger P. Performance Evaluation of Integrated GPS/GIOVE Precise Point Positioning[C]. ION ITM 2010, San Diego, California, USA, 2010 |
| [6] | Hauschild A, Steigenberger P. Combined GPS and Galileo Real-time Clock Estimation with DLR's RETICLE System[C]. ION GNSS, Nashville, USA, 2012 |
| [7] | Langley R B, Banville S, Steigenberger P. First Results:Precise Positioning with Galileo Prototype Satellites[J]. GPS World, 2012, 23(9):45-49 |
| [8] | The System:BeiDou ICD. Galileo-only Positioning[EB/OL]. http://www.gpsworld.com/the-system-beidou-icd-galileo-only-positioning/, 2013 |
| [9] | First Galileo-only Position Fix Performed![EB/OL]. http://www.gpsworld.com/first-galileo-only-position-fix-performed/, 2013 |
| [10] | Septentrio Makes Galileo and Four-Constellation Position Fixes[EB/OL].http://www. gpsworld.com/septentrio-makes-galileo-and-four-constellation-position-fixes/, 2013 |
| [11] | The System:Galileo Autonomous Fix, IndoorNav Standards[EB/OL]. http://www.gpsworld. com/the-system-galileo-logs-first-autonomous-fix/, 2013 |
| [12] | Four Galileo Birds Sighted over Asia[EB/OL]. http://www.gpsworld.com/four-galileo-birds-sighted-over-asia/, 2013 |
| [13] | Weber R. The IGS Multi-Signals Tracking Campaign MGEX—Planning, Status, Perspectives[C]. IGS Workshop 2012, Olstyn, Poland, 2012 |
| [14] | Habrich H, Noll G, Garayt B. Challenges for Data Centers Supporting the Multi-GNSS Experiment[C]. IGS Workshop 2012, Olstyn, Poland, 2012 |
| [15] | Yang Zhe, Song Shuli, Xue Junchen, et al. Accuracy Assessment of Klobuchar Model and NeQuick Model in China[J]. Geomatics and Information Science of Wuhan University, 2012, 37(6):13-18 (杨哲, 宋淑丽, 薛军琛, 等. Klobuchar模型和NeQuick模型在中国地区的精度评估[J]. 武汉大学学报·信息科学版, 2012, 37(6):13-18) |
| [16] | Cui Xizhang, Yu Zongchou, Tao Benzao, et al. Generalized Surveying Adjustment[M]. 2nd ed. Wuhan:Wuhan University Press, 2009 (崔希璋, 於宗俦, 陶本藻, 等. 广义测量平差[M]. 2版. 武汉:武汉大学出版社, 2009) |
 2015, Vol. 40
2015, Vol. 40



