文章信息
- 邓连生, 姜卫平, 李昭, 彭利峰
- DENG Liansheng, JIANG Weiping, LI Zhao, PENG Lifeng
- 电离层高阶项改正对参考框架实现及测站坐标的影响分析
- Analysis of Higher-order Ionospheric Effects on Reference Frame Realization and Coordinate Variations
- 武汉大学学报·信息科学版, 2015, 40(2): 193-198
- Geomatics and Information Science of Wuhan University, 2015, 40(2): 193-198
- http://dx.doi.org/10.13203/j.whugis20130460
-
文章历史
- 收稿日期:2013-09-04
2. 武汉大学卫星导航定位技术研究中心, 湖北 武汉 430079;
3. 卢森堡大学通信技术学院, 卢森堡 L-1359
2. Research Center of GNSS, Wuhan University, Wuhan 430079, China;
3. Faculté des Sciences, de la Technologieet de la Communication, University of Luxembourg, L-1359, Luxembourg
对于GPS信号,由电离层延迟所产生的距离改正在天顶方向最大可达50 m[1],高精度GNSS用户采用双频技术(消电离层组合观测值)来削弱电离层一阶项的影响,剩余的高阶项影响仍然可达2~4 cm[2]。随着GPS技术越来越多地应用于地壳形变监测、板块运动等大地测量高精度研究和应用领域,电离层高阶项延迟的影响备受关注与重视[3,4,5,6]。进行高阶项延迟改正时,需要已知两个条件:信号传播路径上的电子密度以及地磁场强度。应用单层模型假设时,电子密度值可由GPS双频观测值求得,也可由IGS分析中心提供。目前主要用到的地磁模型有两种:国际地磁标准参考场IGRF模型[7,8,9](包括IGRF 11和IGRF 10)和同心倾斜磁偶极子模型[10,11](DIPOLE model)。研究电离层高阶项改正对参考框架和测站坐标影响的大小和变化,分析不同地磁模型下高阶项影响的差异,对于有效控制、改正甚至消除电离层延迟高阶项的影响,从而将GNSS更好地应用于参考框架的建立,实现高精度测量服务,具有重要的实际应用价值和科学意义[12,13,14,15,16,17,18]。
本文首先给出了电离层高阶项改正的基本原理,计算了高阶项延迟对不同GPS观测量的影响;然后利用GAMIT/GLOBK软件和CODE提供的IONEX文件(ftp://cddis.gsfc.nasa.gov/gps/products/ionex)重新解算太阳活动周期高峰年间全球分布的104个IGS基准站观测数据,研究了电离层高阶项改正对参考框架建立和测站坐标变化的影响,并分析了不同地磁模型下影响的差异。 1 电离层高阶项改正原理
GPS卫星发射的电磁波信号穿过电离层时,传播速度会发生变化,不再以光速传播,传播路径也会发生弯曲。其中,路径弯曲对测距结果的影响较小,一般可忽略。考虑载波相位测量原理及GPS信号的双频特征,有如下顾及电离层延迟高阶项的观测方程[10]:
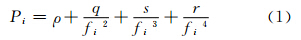
式中,Pi、Li分别为测码伪距和载波相位观测值;fi表示载波频率;ρ为测距码从卫星至接收机的几何距离;电离层项分别为:

其中,B0 表示地磁场强度;Ne为电子密度,即单位体积中所含的电子数,常用“电子数/m2”或“电子数/cm2”来表示; 为GPS信号传播方向的单位向量;η=0.66为形态系数;Nmax= 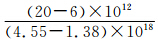 × (TEC-4.55×1018)+20×1012,表示信号传播路径上的最大电子密度。实际计算中,由于地磁场强在单个测站的可视区域中的变化并不显著,因此
× (TEC-4.55×1018)+20×1012,表示信号传播路径上的最大电子密度。实际计算中,由于地磁场强在单个测站的可视区域中的变化并不显著,因此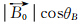 可以提到积分号以外,通过估计某一高度处(本文固定高度设为450 km)的地磁场强值来求得。以上结果可由电磁波在电离层中传播的Appleton-Hartree公式推得。
可以提到积分号以外,通过估计某一高度处(本文固定高度设为450 km)的地磁场强值来求得。以上结果可由电磁波在电离层中传播的Appleton-Hartree公式推得。
由式(1)~式(3)可得顾及电离层延迟高阶项的消电离层组合观测方程:

表 1给出了不同电离层活跃程度下由式(1)~式(5)计算得到的不同观测量的高阶项(二、三阶项)延迟量。其中,TEC值以1016个电子/m2为单位,并将它称为1 TECU;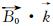 取104 nT,反映在有效电离层高度内估计电子密度沿路径积分时的磁场强度通用值。
取104 nT,反映在有效电离层高度内估计电子密度沿路径积分时的磁场强度通用值。
| TEC值/TECU | |||||
| 1 | 10 | 30 | 50 | 100 | |
| L1伪距高阶项延迟 | 0.23 | 2.31 | 6.93 | 11.54 | 23.08 |
| L2伪距高阶项延迟 | 0.49 | 4.88 | 14.64 | 24.40 | 48.79 |
| L1相位高阶项延迟 | -0.12 | -1.15 | -3.46 | -5.77 | -11.54 |
| L2相位高阶项延迟 | -0.24 | -2.44 | -7.32 | -12.2 | -24.40 |
| LC组合伪距高阶项延迟 | 0.17 | 1.67 | 5.00 | 8.33 | 16.65 |
| LC组合相位高阶项延迟 | 0.08 | 0.83 | 2.50 | 4.16 | 8.33 |
由表 1可知,随着总电子含量的变化,电离层高阶项延迟会有所不同。伪距所受的影响较相位明显,无电离层组合观测值可以在一定程度上削弱高阶项影响。然而,电离层活动剧烈时,其二、三阶项延迟可达cm级,尤其是L2伪距上的延迟量。对于高精度应用,应当顾及电离层高阶项延迟改正。 2 GPS数据处理与分析
地磁场处于相对稳定的水平,电子密度依赖于太阳活动的强度,太阳活动的周期约为11~13 a,故总电子含量也呈现出周期为11 a左右的周期性变化。上一次太阳活动高峰出现在2001年前后,1999~2003年为太阳活动高峰期,在此期间,不但电离层延迟量会加大,而且时而会出现电离层磁暴等异常情况,严重时会影响无线电通信和卫星导航定位系统的正常工作。本文主要对基准站1999~2003年5 a时间内所受的电离层延迟高阶项的影响进行分析,研究电离层活跃期不同地磁模型下高阶项的影响规律,以期对第24个太阳活动高峰期间全球测站变化及参考框架的建立提供参考。
利用GAMIT10.4软件[19]对全球分布的104个IGS基准站在1999~2003年5 a期间的观测数据进行基线解算(解算每周三的观测数据)。数据处理过程中,同时解算卫星轨道、地球定向参数(earth orientation parameter,EOP)、测站坐标,对流层延迟及水平梯度参数。卫星截止高度角设置为10°,并根据验后相位残差对观测值进行重新定权,计算固体潮、海潮、极潮改正,其中海潮负载模型采用FES2004。解算时,充分利用IGS基准站提供的met文件计算静力学延迟初值,使用VMF1投影函数模型[20]和绝对天线相位中心改正模型。为了更加明确地了解不同地磁模型之间的差异所造成的高阶项影响变化的不同,整个数据解算过程分3次进行:无电离层高阶项改正处理(用NO表示)、IGRF11地磁模型下的电离层延迟高阶项改正处理(用IG表示)、DIPOLE地磁场模型下的电离层高阶项改正处理(用ID表示)。参与解算的全球基准站分布及应用于参考框架定义的测站分布如图 1所示,图中标注站名的测站为参考框架定义点。
 |
| 图 1 解算测站及参考框架定义测站分布Fig. 1 Distribution of Processing Sites and Sites in Reference Frame Definition |
本文首先比较统一基准下的NO与IG两组解之间框架转换参数的不同,研究分析电离层延迟高阶项改正对坐标系统间转换参数的影响。对于两组解算获得的单天基线松弛解,基准定义时选取完全相同的IGS核心基准站(如图 1所示),利用GLOBK软件估计HELMERT转换参数,迭代计算后统一基准至ITRF2005框架下,同时获得框架转换参数。在基线处理过程中,由GAMIT解算得到的H文件中的基准站位置关系是一组自洽且具有很好内符合的坐标相对关系,通过同样的参数转换方法并且由同样的基准站提供框架点,统一框架至ITRF框架,因此所得转换参数的不同可以反映出高阶项改正对于参考框架实现的影响。图 2表示NO与IG统一基准时解算得到的框架转换参数作差的结果(NO-IG),图中红色线为单天解结果,黑色线为8周高斯滤波后结果,滤波时以时间间隔加权处理。
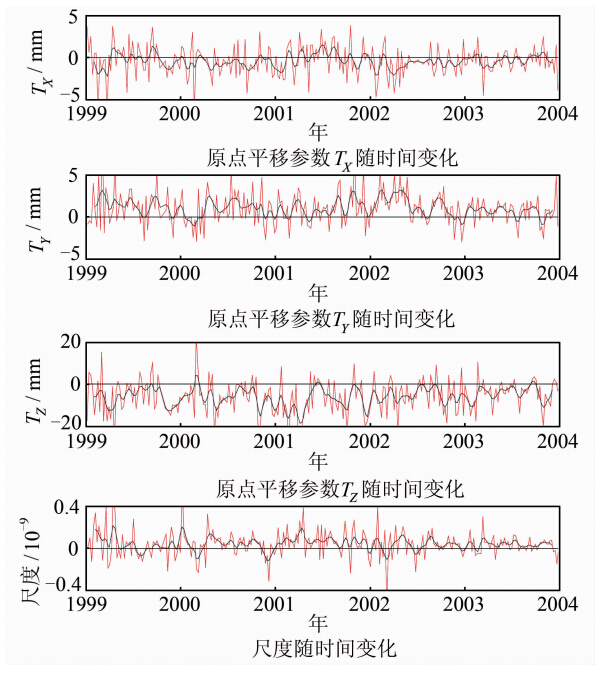 |
| 图 2 高阶项改正引起的基准转换参数变化Fig. 2 Variations of Transformation Parameters After Higher-order Ionospheric Corrections |
由图 2可知,电离层延迟高阶项改正影响了参考框架原点的实现,尤其是Z方向的平移可达20 mm。X、Y方向的平移所受的影响相对较小,基本维持在5 mm以下,X、Y、Z三个方向在观测期间电离层延迟的平均差值分别为0.4 mm、1.0 mm、5.8 mm。尺度所受的影响较小,高阶项改正所导致的尺度差异基本小于0.2×10-9(1.28 mm)。并且各参数改正差值的大小随时间变化与电离层总电子含量变化具有很好的一致性,各参数在1999~2002年间变化剧烈,2002年以后变化趋于平缓。整个观测期间,高阶项改正后,大多数时段X、Z方向的平移参数均增大,而尺度参数和Y方向的平移参数则减小。
在计算电离层延迟二阶项改正时,需要已知穿刺点处的地磁场强。IGRF和DIPOLE两种地磁模型表征地磁场强的方式不同。IGRF是根据全球地磁台站与野外磁测资料、卫星磁测资料综合分析而研制的,通过全球地磁场资料的高斯分析得出了全球地磁场模型,是一个数值模型[7,8,9]。DIPOLE模型是近似模型,用位于地心的一个南北向短磁棒产生的磁场来代表,计算时以赤道附 近的地磁场强(~3.12×10-5 Tesla)为基准,通过计算某点的地磁余纬度,求得该点的地磁场强值[3]。理论上说,IGRF模型比DIPOLE地磁模型更为准确地表征了全球地磁场强的变化,但是DIPLOE地磁模型较易实现,因此早期在研究电离层高阶项对GPS观测的影响时,很多学者利用该模型[3,10,11]。随着计算技术的发展以及IGRF模型的不断精化,IGRF模型逐渐被研究人员所采用[4,13,14,16,17,20]。GAMIT10.4中提供了这两种模型作为备选地磁模型,高精度数据处理软件GIPSY和BERNESE均采用DIPOLE模型来计算电离层高阶项延迟。由于IGRF与DIPOLE实现方式的差异,因此对于同一点处的地磁场强数 值也并不一定完全一致。本文进一步计算了不同地磁模型影响下的高阶项改正,比较分析了不同地磁模型引起的基准转换参数、基准站坐标变化的差异。图 3表示两种地磁模型下的基准转换平移参数Z的变化,图中红色线条表示ID-NO结果,绿色线条表示ID-IG结果,黑色线条为滤波后结果。
 |
| 图 3 地磁模型影响的Z参数变化示意图Fig. 3 Variations of Translation Parameter Z in Different Geomagnetic Model |
对于ID和IG两组松弛解,经HELMERT转换统一基准后,两组对应解之间的参数Z有着约1 cm的变化。从量级上来说,IGRF与DIPOLE两种地磁模型所造成的原点平移Z的变化相当,随时间变化的状态也是一致的,DIPOLE模型下,整个观测期间高阶项改正后大多数时段参数Z也是增加的。
2.2 高阶项改正对测站坐标变化的影响
图 4表示采用DIPOLE模型时全球坐标的整体变化趋势,图中的数值是由1999~2003年的单天基线解通过GLOBK卡尔曼滤波估计得到的最终坐标值。从图 4可看出,从平面方向来说,高纬度测站有着向北偏的趋势,而赤道区域测站则向南移,且赤道附近的偏移值大于其他纬度地区;从高程前后的变化角度分析,北半球大多数测站高程增加,而南半球大多数测站高程则减小;我国境内中纬度IGS站均有向南偏移的现象,且向南偏移的变化相对稳定在正南方向,东西方向则变化较小,这与刘西凤的研究结果也是一致的[21]。
 |
| 图 4 DIPOLE地磁模型下测站坐标变化图Fig. 4 Coordinates’ Difference in DIPOLE Model |
图 5表示ID和IG两组解的全球坐标差异。尽管两种地磁模型影响下基准站坐标变化的趋势特征是相似的,但是两组解的坐标作差后,除U方向差距不大外,平面方向坐标变化趋势与高阶项改正下的趋势有所不同。整体上,北半球的测站有着向北偏移的趋势,而南半球则向南偏移,这表明两种地磁模型的改正量存在差异。使用DIPOLE模型时,在南半球与赤道附近,高阶项(主要是二阶项)改正比IGRF小;在北半球的改正,两种模型是基本相当的。需要指出的是,在东南亚地区、非洲南端和南大西洋地区,两种模型下的高阶项改正的差异很显著。由于ID和IG两组解之间的差异仅仅为地磁模型不同,联合高阶项改正公式,两组解下测站坐标的变化反映了两种地磁模型在不同区域地磁场强的差异。
 |
| 图 5 地磁模型不同引起的测站坐标变化图Fig. 5 Coordinates’ Difference Between IGRF and DIPOLE Model |
电离层延迟高阶项影响分析是进一步提高GNSS高精度服务范围的重要基础。本文确定了高阶项延迟对不同GPS观测的影响量,研究了电离层高阶项改正对参考框架和测站坐标影响的大小和变化,分析了当前常用的两种地磁模型下高阶项影响的差异。
本文的结果表明,不同的地磁模型下,电离层高阶项的影响存在差异,相同地磁模型下,电离层高阶项影响在全球范围内的分布也不均匀。由高阶项改正的基本原理,电离层高阶项延迟影响的大小主要由信号传播路径上的地磁场强以及电子密度(总电子含量)所决定。因此,导致不同影响的原因在于地磁模型以及电子密度值的差异。本文的分析结果可以反映地磁模型的不同以及电子密度值的变化对电离层高阶项分析的影响。电子密度值和地磁场强值在不同区域均有不同的变化,两种外部数据源的空间变化导致了电离层高阶项影响在全球范围内的分布不均匀。相较于电子密度值的年际变化及差异来说,地磁场强处于相对稳定的水平,电离层高阶项延迟影响随时间的变化则更多地反映了电子密度值变化的影响。在同一电子密度值区域,地磁模型的最优表征影响着高阶项延迟量。因此,关于局部区域地磁场和电子密度值的建模对于进一步揭示电离层高阶项延迟的影响差异是必要的。
致谢:感谢美国麻省理工学院(MIT)授权使用GAMIT/GLOBK软件包,以及Elizabeth J.Petrie博士在本文GPS数据处理过程中给予的建议和帮助。
| [1] | Li Zhenghang, Huang Jinsong. GPS Surveying and Data Processing[M]. Wuhan:Wuhan University Press, 2010(李征航, 黄劲松.GPS测量与数据处理[M].武汉:武汉大学出版社, 2010) |
| [2] | Wei Ziqing, Ge Maorong. Mathematical Model of GPS Relative Positioning[M]. Beijing:Survey Press, 1998(魏子卿, 葛茂荣. GPS相对定位的数学模型[M].北京:测绘出版社, 1998) |
| [3] | Bassiri S, Hajj G A. Higher-order Ionospheric Effects on the Global Positioning System Observables and Means of Modeling Them[J]. Geoid, 1993, 18:280-289 |
| [4] | Hernández-Pajares M, Juan J M, Sanz J, et al. Second-order Ionospheric Term in GPS:Implementation and Impact on Geodetic Estimates[J]. J Geophys Res, 2007, 112, B08417, doi:10.1029/2006JB004707 |
| [5] | Palamartchouk K. Apparent Geocenter Oscillations in Global Navigation Satellite Systems Solutions Caused by the Ionospheric Effect of Second Order[J]. J Geophys Res, 2010, 115:B03415, doi:10.1029/2008JB006099 |
| [6] | Li Zhenghang, Chen Kai, Liu Wanke, et al. Ionospheric Delay Model Containing f3 Term[J]. Geomatics and Information Science of Wuhan University, 2007, 32(2):139-143(李征航, 陈锴, 刘万科, 等. 顾及f3项的电离层延迟模型[J].武汉大学学报·信息科学版, 2007, 32(2):139-143) |
| [7] | Huang Xiaoying, Bian Shaofeng. The Research Evolution of International High-resolution Geomagnetic Models[J]. Hydrographic Surveying and Charting, 2010, 30(3):79-82(黄晓颖, 边少锋.国际高精度地磁模型研究进展[J].海洋测绘, 2010, 30(3):79-82) |
| [8] | Chen Bin, Gu Zuowen, Di Chuanzhi, et al. International Geomagnetic Reference Field:the Eleven Generation[J]. Recent Development in World Seismology, 2012, 398(2):20-29(陈斌, 顾左文, 狄传芝, 等. 第11代国际地磁参考场[J].国际地震动态, 2012, 398(2):20-29) |
| [9] | IAGA, Working Group V-MOD. International Geomagnetic Reference Field:the Eleventh Generation[J]. Geophys Res Lett, 2010, 183:1 216-1 230 |
| [10] | Fritsche M, Dietrich R, Knofel C, et al. Impact of Higher-order Ionospheric Terms on GPS Estimates[J].Geophys Res Lett, 2005, 32(23), doi:10.1029/2005GL024342 |
| [11] | Kedar S, Hajj G A, Wilson B D, et al.The Effect of the Second Order GPS Ionospheric Correction on Receiver Positions[J].Geophys Res Lett , 2003, 30(16):1 829, doi:10.1029/2003GL017639 |
| [12] | Steigenberger P, Rothacher M, Dietrich R, et al. Reprocessing of a Global GPS Network[J]. J Geophys Res, 2006, 111:B05402 |
| [13] | Li Zhenghang, Chen Kai, Liu Wanke, et al. Mathematical Unification and Method Expansion of GNSS Ionospheric Delay Model[J]. Geomatics and Information Science of Wuhan University, 2007, 32(8):699-703(李征航, 陈锴, 刘万科, 等. GNSS电离层延迟模型的数学统一与方法扩展[J].武汉大学学报·信息科学版, 2007, 32(8):699-703) |
| [14] | Zheng Lei, Chen Kai, Li Zhenghang, et al. Analysis of Effect of f3 Term and Mapping Function on Ionospheric Delay[J]. Journal of Geodesy and Geodynamics, 2008, 28(5):100-108(郑磊, 陈锴, 李征航, 等. f3项与投影函数对电离层延迟的影响[J].大地测量与地球动力学, 2008, 28(5):100-108) |
| [15] | Zhang Xiaohong, Li Zhenghang, Cai Changsheng. Study on Regional Ionospheric Model Using Dual-frequency GPS Measurements[J]. Geomatics and Information Science of Wuhan University, 2001, 26(2):140-143(张小红, 李征航, 蔡昌盛. 用双频GPS 观测值建立小区域电离层延迟模型研究[J].武汉大学学报·信息科学版, 2001, 26(2):140-143) |
| [16] | Zhang Shuangcheng, Tu Rui, Zhang Qin, et al. The Establishment of Ionospheric Second-order Model and the Analysis of Ionospheric Variation[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40:105-110(张双成, 途锐, 张勤, 等.电离层二阶项模型的构建及其变化规律分析研究[J].测绘学报, 2011, 40:105-110) |
| [17] | Liu Xifeng, Yuan Yunbin, Huo Xingliang, et al. Model Analysis Method (MAM) on the Effect of the Second-order Ionospheric Delay on GPS Positioning Solution[J]. Chinese Science Bull, 2010, 55(12):1 162-1 167(刘西凤, 袁运斌, 霍星亮, 等.电离层二阶项延迟对GPS 定位影响的分析模型与方法[J].科学通报, 2010, 55(12):1 162-1 167) |
| [18] | Jiang Weiping, Zou Xuan, Tang Weiming. A New Kind of Real-time PPP Method for GPS Single-frequency Receiver Using CORS Network[J]. Chinese Journal of Geophysical Research, 2012, 55(5):1 549-1 556(姜卫平, 邹璇, 唐卫明.基于CORS网络的单频GPS实时精密单点定位新方法[J].地球物理学报, 2012, 55(5):1 549-1 556) |
| [19] | King R W, Bock Y. Documentation for the GAMIT Analysis Software Release 10.4 [M]. Cambridge, MA:Mass Inst Technol, 2010 |
| [20] | Petrie E J, King M A, Moore P, et al. Higher-order Ionospheric Effects on the GPS Reference Frame and Velocities[J]. J Geophys Res, 2010, 115:B03417 |
| [21] | Liu Xifeng, Yuan Yunbin. Preliminary Analysis on the Effect of Second-order Ionospheric Delay on GPS Positioning Solution Over the Mid-low Latitude Regions in China[J].Science in China:Sinca Physica, Mechanica & Astronomica, 2010, 40(5):658-662(刘西风, 袁运斌. 我国中低纬地区GPS定位中的电离层二阶项延迟影响分析与研究[J].中国科学:物理学力学天文学, 2010, 40(5):658-662) |
 2015, Vol. 40
2015, Vol. 40


