文章信息
- 姚宜斌, 余琛, 胡羽丰, 刘强
- YAO Yibin, YU Chen, HU Yufeng, LIU Qiang
- 利用非气象参数对流层延迟估计模型加速PPP收敛
- Using Non-meteorological Parameters Tropospheric Delay Estimation Model for Accelerating Convergence of PPP
- 武汉大学学报·信息科学版, 2015, 40(2): 188-192
- Geomatics and Information Science of Wuhan University, 2015, 40(2): 188-192
- http://dx.doi.org/10.13203/j.whugis20130584
-
文章历史
- 收稿日期:2013-10-17
卫星电磁波信号从发射到接收机接收期间,受大气影响必然会产生大气延迟。在GNSS导航定位中,将大气延迟分为两类,即延迟量与信号频率无关的对流层延迟和与频率有关的电离层延迟。电离层延迟可以利用双频观测值组成无电离层组合模型有效消除,所以如何正确估计并改正对流层延迟是高精度GNSS导航定位的重要课题之一。以往对对流层延迟的估计需要借助实测气象参数,这无疑对定位带来了不便。随着观测手段的革新以及观测数据序列的积累,许多学者和机构相继研究出了精度较高且不需借助实测气象参数的全球对流层延迟估计模型。
在导航定位中,一般将信号在对流层传播路径上的斜延迟通过映射函数投影到天顶方向,因此,通常对天顶对流层延迟(zenith tropospheric delay,ZTD)进行建模。Collins和Langley[1]为美国广域增强导航系统的推广应用建立了UNB模型,经过不断发展改进,形成了UNB1-4、UNB3m、UNB.na等系列模型,但这种模型只考虑了ZTD的纬向变化,全球平均偏差3~5 cm。EGNOS模型是欧盟星基广域增强系统采用的天顶对流层延迟改正模型,其精度总体上与采用实测气象参数的Hopfield和Saastamoinen模型相当[2]。李薇等根据美国国家环境预报中心(national centers for environmental prediction,NCEP)再分析资料采用三维空间参数表构建了最新的IGGtrop全球对流层延迟经验模型,精度有明显改善[3]。姚宜斌等人利用GGOS(global geodetic observing system)Atmosphere提供的全球天顶对流层延迟格网数据,使用球谐函数建立全球非气象参数对流层天顶延迟模型(global zenith tropospheric delay,GZTD),其精度与IGGtrop相当,全球平均偏差仅为0.2 cm,但模型所用的参数较IGGtrop模型有大幅度减少[4]。这些模型都是在不需要外部条件的情况下将某一时间段已有的全球范围内的对流层延迟数据利用某种数学模型拟合出的一套高精度的、便于应用的 ZTD估计函数。McGraw通过多组对比试验认为,在向多频多系统导航定位发展过程中,更可靠的对流层延迟模型将有助于改善导航的定位水平[5]。
精密单点定位技术(precise point positioning,PPP)已广泛应用于精密定轨、GPS气象学以及精密授时等领域,并得到了良好的效果[6]。但是在采用无电离层组合观测值的传统PPP解算中,需要经过30 min左右的收敛时间才能达到cm级的定位精度[7]。如何加快收敛时间,已经成为限制PPP发展的关键问题[8]。传统PPP对于对流层延迟的处理是利用标准气象参数的Saastamoinen模型改正干延迟,然后将残余的湿延迟作为待估参数,利用随机游走的方法同坐标参数一起估计。本文将自主研发的GZTD模型应用到PPP中,将GZTD计算出的对流层延迟改正到伪距和相位观测值上,从而不估计对流层延迟参数,从定位精度特别是收敛时间两方面研究非气象参数对流层延迟估计模型在PPP中的应用效果。 1 非气象参数对流层延迟估计模型 1.1 GZTD模型的建立
通过对GGOS提供的全球天顶对流层延迟格网数据的时空分布特性进行分析可知,ZTD存在年周期变化和半年周期变化,且受高度变化的影响,同时还与纬度有关。首先将全球日平均ZTD格网时间序列按式(1)进行拟合:
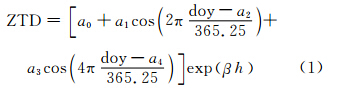
式中,doy为年积日;h为高度;a0、a1、a3分别为在海平面上的ZTD年均值、年周期变化振幅和半年周期变化振幅;a2、a4分别为年周期变化和半年周期变化相位,在GPT模型[9]和GWMT模型[10]中,a2一般取固定值28,但在建立GZTD过程中,将其参数化处理,以提高模型精度;β为将h高度处的ZTD改正到海平面处的改正常数,取经验值-0.000 131 37。
然后估计不同区域位置的差异,采用10阶10次的球谐函数将上述5个参数进行球谐展开,
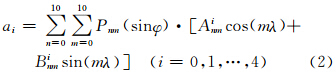
其中,Pnm为勒让德多项式;φ和λ分别为格网点纬度和经度;Anmi和Bnmi为使用最小二乘确定的球谐函数n阶m次系数(共5×121个非零系数)。
使用以上球谐函数展开ZTD变化特征参数建立的全球天顶对流层延迟ZTD模型,不仅建模方法简洁,计算简便,且该模型能有效地反映天顶对流层延迟经向、纬向和高程方向的空间变化特征。 1.2 传统精密单点定位模型
精密单点定位是利用精度较高的精密星历和精密钟差产品,将尽可能多的误差项,如固体潮、天线相位缠绕误差、天线相位中心偏差等利用较为精确的模型进行改正,将对流层湿延迟当作未知参数用随机游走或分段线性的方法进行估计,从而达到cm甚至mm级的定位精度[11]。GPS的观测值包括伪距和相位,基本观测方程可以参照Teunissen和Kleusberg给出的形式[12],天顶干延迟(利用标准气象参数Saastamoinen模型计算)已经事先改正,则观测方程可以写为:
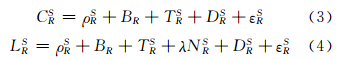
式中,上、下标S、R分别代表卫星、测站编号;LRS和CRS分别为无电离层组合相位和伪距观测值;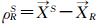 代表卫星与测站之间的几何距离;BR代表接收机钟差;TRS代表信号传播路径上的对流层湿延迟;λ为无电离层组合观测值对应的波长;NRS为无电离层组合整周模糊度,以周为单位;DRS代表天线相位中心偏差、硬件延迟及多路径效应等的影响;εRS代表观测值噪声。以上模型中,相位初始偏差包含在模糊度参数中[13],卫星星历和伪距的双频码偏差DCB已经利用IGS提供的产品事先改正。传统定位模型将天顶对流层延迟作为参数进行估计,其优点是保证了定位结果在高程方向上的精度,得到一个精度较高的天顶对流层延迟产品,避免了引入估计模型而带来的模型误差。
1.3 无大气延迟的精密单点定位模型
代表卫星与测站之间的几何距离;BR代表接收机钟差;TRS代表信号传播路径上的对流层湿延迟;λ为无电离层组合观测值对应的波长;NRS为无电离层组合整周模糊度,以周为单位;DRS代表天线相位中心偏差、硬件延迟及多路径效应等的影响;εRS代表观测值噪声。以上模型中,相位初始偏差包含在模糊度参数中[13],卫星星历和伪距的双频码偏差DCB已经利用IGS提供的产品事先改正。传统定位模型将天顶对流层延迟作为参数进行估计,其优点是保证了定位结果在高程方向上的精度,得到一个精度较高的天顶对流层延迟产品,避免了引入估计模型而带来的模型误差。
1.3 无大气延迟的精密单点定位模型
将GZTD计算出的对流层延迟直接改正到伪距和相位观测值上,可以得到无大气延迟参数的精密单点定位模型:
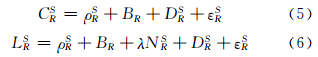
可以看出,无大气延迟参数模型的观测方程待估参数少了一个,当观测卫星数仅有4颗时,也可以保证系数矩阵满秩。这种方法减少了参数个数,对于整周模糊度的分离与固定有较大帮助,有可能会加快精密单点定位的收敛时间。另一方面,如果所应用的非气象参数对流层延迟估计模型具有较高的精度,其定位精度较传统精密单点定位不会有大的损失。
本文采用卡尔曼滤波实现以上模型,在没有发生周跳的情况下,模糊度参数是常数,坐标参数的状态根据测站的运动情况来确定,静态定位中将其当作常数处理。接收机钟差视为白噪声。用于对比分析的传统模型中的湿延迟参数利用随机游走方法进行估计,投影函数选择NMF模型[14]。 2 实验与分析
为了验证非气象参数的对流层延迟估计模型在精密单点定位中的应用效果,选取了全球分布的20个IGS跟踪站(图 1),首先利用TEQC编辑并剔除含有粗差的数据,然后用自主研发的PPP软件Passion计算了2011年全年的数据,得到每个站当天的单天解。从定位精度和收敛时间两个方面对两种模型的计算结果进行了分析。
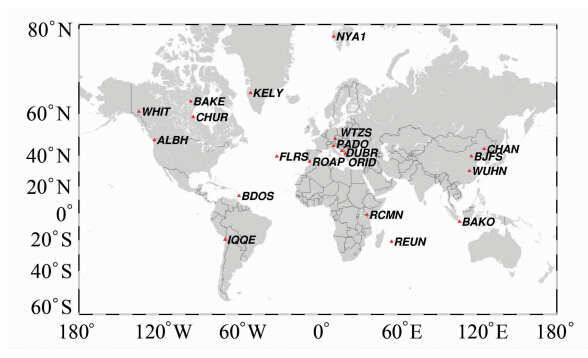 |
| 图 1 IGS站点全球分布图Fig. 1 Worldwide Distribution of IGS Sites |
为了便于对比分析两种方法的精度差异,对于单天定位解,采用MAE指标进行统计,
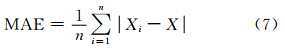
其中,Xi是收敛以后参与计算的第i个历元的定位结果;X是真值(由IGS分析中心提供);n是收敛以后参与计算的历元数。 实际应用中,静态PPP解算的定位精度常用定位偏差 (bias)来评定,
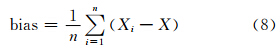
与 MAE不同的是,bias可以正负相互抵消,从而可以通过平滑得到较好的单天解精度。在数量上,bias普遍比MAE要小。
对于收敛时间,本文规定,从开始解算的历元找起,如果某一历元的平面偏差小于10 cm,天顶方向偏差小于15 cm,并且从这一历元往后的连续20个历元的平均偏差也满足此要求,则从定位起始到该历元所需的观测时间即为收敛时间。 2.1 定位精度的对比
由于对流层延迟对天顶方向坐标参数的影响较大,对平面方向坐标参数的影响较小,故传统模型和无大气延迟模型的精度区别主要体现在天顶方向上。图 2显示了利用两种模型计算出的各站平均单天解平面方向的MAE。可以看出,平面MAE都保持在5 cm以内,两种模型平均MAE之差基本都在1 cm以内,没有明显差异。另外,两种模型全年平面定位的平均偏差分别为1.12 cm和1.13 cm,仅差别0.1 mm,这表明利用了非气象参数对流层延迟估计参数后,精密单点定位的平面定位精度基本不变。这一方面是因为对流层延迟本身就对平面方向的定位精度影响较小;另一方面,由于在建立非气象参数对流层估计模型中,所用的数据在全球分布的水平分辨率较高,且分布均匀,故平面精度较高。
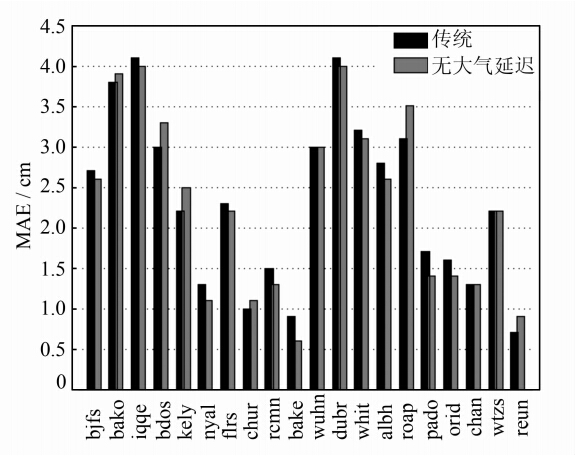 |
| 图 2 平面方向日平均精度对比Fig. 2 Comparison of Day Average Precision in Planar Direction |
图 3显示了利用两种模型计算出的各站平均单天解天顶方向的MAE。可以看出,传统模型的天顶坐标参数精度略优于无大气延迟模型,但两者差距大都保持在1 cm以内,平均差异为0.48 cm。经过统计,两种模型全年天顶方向的平均偏差分别为1.98 cm和2.11 cm,传统模型比无大气延迟模型的定位偏差小1.3 mm,这表明非气象参数对流层估计模型对精密单点定位的天顶方向精度的影响相对较大,但在允许范围以内。同平面方向不同,对流层延迟对天顶方向的影响 较大,并且非气象参数模型建立所用的数据垂直分辨率较低,不能精细表达延迟与高程的关系,故在天顶方向上的精度相对较低。由于实际应用中,精密单点定位在不固定模糊度的情况下,天顶方向的定位偏差约为±2 cm,也在可容许范围之内。随着对流层观测资料垂直分辨率的提高,通过进一步精化GZTD模型,这一影响会逐渐减弱。
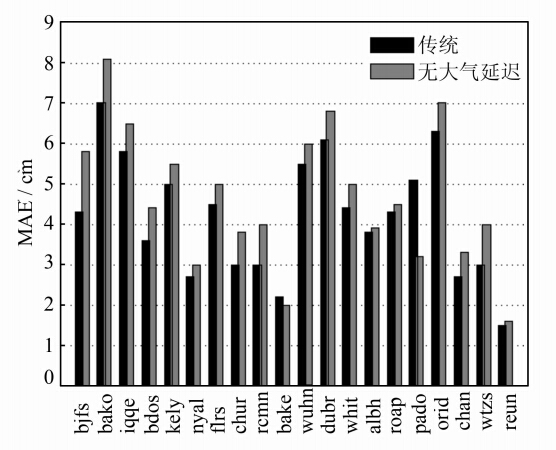 |
| 图 3 天顶方向日平均精度对比Fig. 3 Comparison of Day Average Precision in Zenith Direction |
图 4显示了BAKO等4个IGS站2011年1月15日天顶方向坐标参数收敛时间上的改善情况。横坐标表示定位时间,纵坐标表示定位偏差MAE。可以看出,无大气延迟模型在定位初期的偏差比传统模型要小,特别是首历元,其定位精度一般要比传统模型高一个数量级,从而比传统模型收敛更快,且在收敛以前,偏差的变化相对于传统模型更为平滑,不会出现较大甚至剧烈的波动。随着观测时间加长,特别是在收敛以后,无大气延迟模型与传统模型的定位结果趋于一致。图 4中显示的4个站中较明显的BAKO站,在定位开始时,无大气延迟模型就能很快收敛到cm级,并没有较大幅度的波动,而传统模型则存在40 cm的大波动,减慢了收敛时间。改善程度相对较弱的NYA1站虽然都有一个大的波动,但传统模型的波动幅度接近40 cm,而无大气延迟模型方法的波动幅度仅为20 cm,缩小了近一倍。
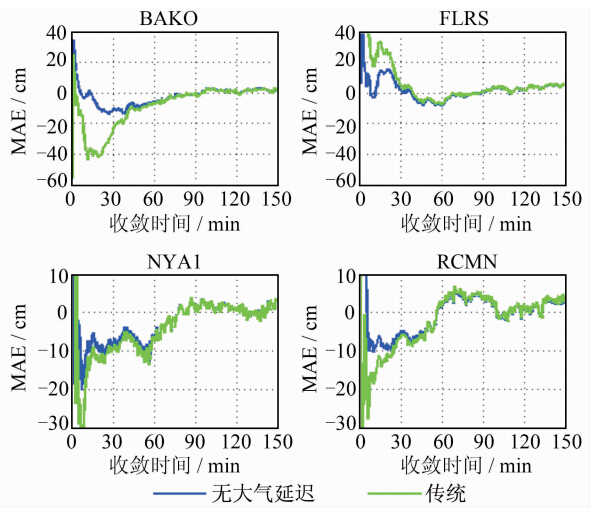 |
| 图 4 第15天部分站不同模型定位收敛情况对比Fig. 4 Comparison of Convergence Time in Different Models on Some Stations at DOY 015 |
图 5显示了各站平均收敛时间的对比,其中无大气延迟模型的收敛时间明显短于传统模型,两者差距最大可达8.5 min。两种模型的平均收敛时间分别为20.55 min和15.875 min,无大气延迟模型比传统模型收敛加快了约23%。非气象参数对流层延迟估计模型十分有效地缩短了精密单点定位解算的收敛时间,而较快的收敛时间对于整周模糊度的固定有很大的帮助。
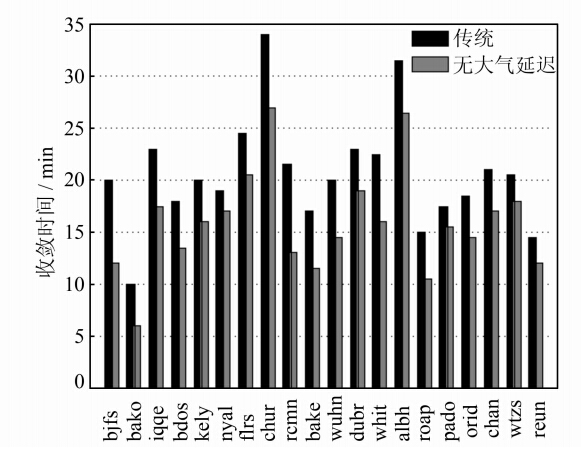 |
| 图 5 各站不同模型的收敛时间对比Fig. 5 Comparison of Convergence Time in Different Models on All Stations |
图 6显示了BJFS站14号卫星和18号卫星模糊度收敛时间的对比。横坐标表示定位时间,纵坐标表示各历元模糊度大小。此处的模糊度均为浮点解,因为模糊度参数会吸收一些未模型化的误差,如硬件延迟等,受其影响,两种方法计算所得的模糊度可能略有差异。在实际观测中,因为存在周跳以及测站视线等原因,模糊度参数会频繁地进行重收敛。无大气延迟模型在收敛期间模糊度参数的变化较平缓,并能很快收敛,表 1统计了图 6所示卫星模糊度收敛期间的标准差,无大气延迟相对于传统模型改善均在50%以上。同天顶方向的坐标参数一样,随着观测时间的增长,两种模型趋于一致。这充分说明无大气延迟模型能使模糊度参数与其他参数更快分离,并很快收敛,对快速固定有着重要意义。
| 传统模型/m | 无大气延迟/m | 改善程度/% | |
| PRN14时段1 | 0.109 | 0.018 | 80 |
| PRN14时段2 | 0.107 | 0.050 | 53 |
| PRN18时段1 | 0.142 | 0.024 | 83 |
| PRN18时段2 | 0.044 | 0.009 | 79 |
 |
| 图 6 BJFS站2颗卫星不同时间段 的模糊度参数收敛情况对比Fig. 6 Comparison of the Ambiguity Convergence in Different Models on Some Stations |
本文主要研究了非气象参数对流层延迟估计模型在精密单点定位中的应用,通过实验分析对比了应用非气象参数对流层延迟估计模型得到的无大气延迟精密单点定位模型和传统精密单点定位模型在精度和收敛时间两方面的异同。
1)无大气延迟模型与传统模型在平面方向的精度相当,在天顶方向上传统模型略优,但其差异很小,且在容许范围之内。总的来说,将非气象参数估计模型应用到精密单点定位中,可以达到预期的精度要求。
2)利用无大气延迟模型显著改善了精密单点定位计算初期的性能,使精密单点定位的收敛时间加快了约23%,在短时间内就能获得良好的定位精度。
3)无大气延迟模型改善了模糊度的收敛及重收敛过程,在发生周跳或有新卫星加入时,能更快地使模糊度参数收敛,加速模糊度的固定。
随着模型的精化和对流层观测资料的不断丰富,尤其是垂直分辨率较高的观测资料的增多,非气象参数对流层延迟估计模型的精度也会不断提高,对精密单点定位的作用也会越来越大。
| [1] | Li W, Yuan Y B, Ou J K, et al. A New Global Zenith Tropospheric Delay Model IGGtrop for GNSS Applications[J]. Chinese Science Bulletin, 2012, 57(17):2 132-2 139 |
| [2] | Qu W J, Zhu W Y, Song S L, et al. Evaluation of the Precision of Three Tropospheric Delay Correction Models[J]. Chinese Astronomy and Astrophysics, 2008, 32(4):429-438 |
| [3] | Li W, Yuan Y B, Ou J K, et al. A New Global Zenith Tropospheric Delay Model IGGtrop for GNSS Applications[J]. Chinese Science Bulletin, 2012, 57(17):2 132-2 139 |
| [4] | Yao Yibin, He Changyong, Zhang Bao, et al. A New Global Zenith Tropospheric Delay Model GZTD[J]. Chinese Journal of Geophysics, 2013, 56(7):2 218-2 227(姚宜斌, 何畅勇, 张豹, 等. 一种新的全球对流层天顶延迟模型 GZTD[J]. 地球物理学报, 2013, 56(7):2 218-2 227) |
| [5] | McGraw G A. Tropospheric Error Modeling for High Integrity Airborne GNSS Navigation[C]. Position Location and Navigation Symposium (PLANS), 2012 IEEE/ION, Myrtle Beach, SC, 2012 |
| [6] | Kouba J. A Possible Detection of the 26 December 2004 Great Sumatra-Andaman Islands Earthquake with Solution Products of the International GNSS Service[J]. Studia Geophysica et Geodaetica, 2005, 49(4):463-483 |
| [7] | Zhang X, Li X X, Guo F. Satellite Clock Estimation at 1 Hz for Realtime Kinematic PPP Applications[J]. GPS Solutions, 2011, 15(4):315-324 |
| [8] | Bisnath S, Gao Y. Current State of Precise Point Positioning and Future Prospects and Limitations[M].Berlin, Heidelberg:Springer, 2008:615-623 |
| [9] | Böhm J, Heinkelmann R, Schuh H. Short Note:A Global Model of Pressure and Temperature for Geodetic Applications[J]. Journal of Geodesy, 2007, 81(10):679-683 |
| [10] | Yao Y B, Zhu S, Yue S Q. A Globally Applicable, Season-specific Model for Estimating the Weighted Mean Temperature of the Atmosphere[J]. Journal of Geodesy, 2012, 86(12):1 125-1 135 |
| [11] | Ye Shirong, Zhang Shuangcheng, Liu Jingnan. Precision Analysis of Precise Point Positioning Based Tropospheric Delay Estimation[J]. Geomatics and Information Sciences of Wuhan University, 2008, 33(8):788-791(叶世榕, 张双成, 刘经南. 精密单点定位方法估计对流层延迟精度分析[J]. 武汉大学学报· 信息科学版, 2008, 33(8):788-791) |
| [12] | Teunissen P J G. GPS for Geodesy[M]. Berlin:Springer, 1998 |
| [13] | Ge M, Gendt G, Rothacher M, et al. Resolution of GPS Carrier-phase Ambiguities in Precise Point Positioning (PPP) with Daily Observations[J]. Journal of Geodesy, 2008, 82(7):389-399 |
| [14] | Niell A E. Global Mapping Functions for the Atmosphere Delay at Radio Wavelengths[J]. Journal of Geophysical Research:Solid Earth (1978-2012), 1996, 101(B1):3 227-3 246 |
 2015, Vol. 40
2015, Vol. 40


