快速检索        
  武汉大学学报·信息科学版  2015, Vol. 40 Issue (2): 176-181

文章信息

许闯, 吴云龙, 罗志才, 刘焱雄, 赵珞成
XU Chuang, WU Yunlong, LUO Zhicai, LIU Yanxiong, ZHAO Luocheng
基于短时间序列重力观测数据的潮汐改正方法
A Tidal Correction Method from a Short-time Series of Gravity Observations
武汉大学学报·信息科学版, 2015, 40(2): 176-181
Geomatics and Information Science of Wuhan University, 2015, 40(2): 176-181
http://dx.doi.org/10.13203/j.whugis20130481

文章历史

收稿日期：2013-09-09
 Abstract              PDF               Figures               Tables
引用本文 0
许闯, 吴云龙, 罗志才, 刘焱雄, 赵珞成. 基于短时间序列重力观测数据的潮汐改正方法[J]. 武汉大学学报·信息科学版, 2015, 40(2): 176-181.
XU Chuang, WU Yunlong, LUO Zhicai, LIU Yanxiong, ZHAO Luocheng. A Tidal Correction Method from a Short-time Series of Gravity Observations[J]. Geomatics and Information Science of Wuhan University, 2015, 40(2): 176-181.
基于短时间序列重力观测数据的潮汐改正方法
许闯1, 吴云龙2 , 罗志才1,3, 刘焱雄4, 赵珞成1    
1. 武汉大学测绘学院, 湖北 武汉 430079;
2. 中国地震局地震研究所(中国地震局地震大地测量重点实验室), 湖北 武汉 430071;
3. 武汉大学地球空间环境与大地测量教育部重点实验室, 湖北 武汉 430079;
4. 国家海洋局第一海洋研究所海洋测绘与工程信息研究中心, 山东 青岛 266061
收稿日期:2013-09-09
基金项目：国家重大科学仪器设备开发专项资助项目(2012YQ10022507);国家自然科学基金资助项目(41374044, 41304018);中国地震局地震科技星火计划项目攻关课题联合资助项目(XH14036).
第一作者:许闯, 博士生, 现主要从事重力反演方面的研究。E-mail:xuchuang526610@163.com
*通讯作者: 吴云龙，博士。E-mail: yunlongwu@gmail.com
摘要：对于没有长期连续潮汐观测站和无精密潮汐模型的地区, 研究高精度潮汐改正方法具有重要意义。给出了基于短时间序列重力观测数据的高精度潮汐改正方法, 并利用全球动力学计划中TIGO Concepcion、Kamioka和Hsinchu三个台站的超导重力观测数据对该方法进行了试验分析。研究结果表明, 利用一天或数天重力观测数据可建立高精度潮汐模型, 其振幅因子和相位延迟解算精度分别优于0.01和0.5°, 潮汐改正精度可以达到μGal量级, 验证了该方法的正确性和有效性。本文方法为无精密潮汐模型区域的潮汐改正提供了新的途径。
关键词： 潮汐     重力观测数据     潮汐改正     短时间序列    
A Tidal Correction Method from a Short-time Series of Gravity Observations
XU Chuang1, WU Yunlong2 , LUO Zhicai1,3, LIU Yanxiong4, ZHAO Luocheng1    
1. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China;
2. Key Laboratory of Earthquake Geodesy, Institute of Seismology, CEA, Wuhan 430071, China;
3. Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, Wuhan University, Wuhan 430079, China;
4. Ocean Geomatics Center, the First Institute of Oceanography, Qingdao 266061, China
Abstract:Areas without standing and continuous tidal data or a precise tidal model require a a precise tidal correction method. High-accuracy tidal correction methods using short-time series of gravity obs- ervations are proposed to address this problem. The superconducting gravity observations of TIGO Concepcion, Kamioka, and Hsinchu stations in Global Geodynamics Project were used in experimental analysis. The results show that:a high-accuracy tidal model can be established by gravity observations over one or several days;the accuracies of factor amplitude and phase delay are better than 0.01 and 0.5 degrees;the accuracy of tidal correction can reach micro gal level, demonstrating the effectiveness of the method. This new approach is suitable for areas without precise tidal models.
Key words: tide     gravity observations     tidal correction     short-time series    

高精度的重力观测数据在大地测量学、地球物理学和地球动力学等领域有着广泛的应用和研究价值。目前，重力测量精度已经达到μGal量级，甚至更高，而潮汐的影响量级可达几十至几百μGal，是精密重力测量中的最主要改正量[1,2,3]。因此，研究精密重力测量的潮汐改正方法具有重要的意义。

现有的潮汐改正方法主要是利用已有的潮汐模型计算测点的潮汐影响值[4,5,6,7,8,9,10,11,12,13]。文献[14]基于理论地球模型、SChwiderski的大洋潮图和我国沿海的局部潮图估算了我国境内的重力潮汐值，精度达到2 μGal。文献[15]利用全球超导重力观测资料验证了合成潮汐参数的实用性，但在海陆交界地区需要更密的格网，内插时也要经过特殊处理。文献[16]的研究结果表明，在近海和岛屿地区进行高精度海岛礁相对重力测量时，必须考虑精确的固体潮和海洋负荷潮改正，从而提高相对重力测量的联测精度。这些精密重力测量的潮汐改正方法均依赖于高精度潮汐模型，文献[17]已经证明，要使潮汐改正的精度达到μGal级，则潮汐模型中潮汐因子的精度应达到0.01，相位延迟为0.5°。但是建立较高精度的潮汐模型一般需要数月或更长时间序列的连续重力潮汐观测数据，对于没有长期连续潮汐观测站和现有潮汐模型精度较低的地区(如海岛和沿海地区等)，这些方法的适用性无法得到保证。因此，利用短时间序列重力观测数据实现高精度潮汐改正已经成为迫切需要解决的问题。

本文给出了基于短时间序列重力观测数据的潮汐改正方法(tidal correction method from short-time series of gravity observations，TCMSSGO)，可以利用一天或数天的重力观测数据实现高精度潮汐改正，并以全球动力学计划(global godynamics poject,GGP)的三个超导重力台站的实际重力观测数据为实例验证了该方法的正确性和有效性。 1 潮汐改正方法

基于短时间序列重力观测数据的潮汐改正方法的基本思路如图 1所示。首先计算短时间序列重力观测数据相对理论固体潮的时间延迟和尺度因子，然后根据尺度因子计算出长时间序列的重力数据，最后采用调和分析方法求出潮汐因子和相位延迟，即可建立潮汐模型，实现潮汐改正。

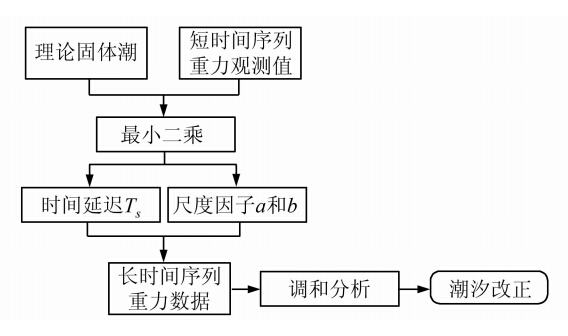图 1 基于短时间序列重力观测数据的潮汐改正方法流程图Fig. 1 Flow Chart for Tidal Modeling from Sort-time Series of Gravity Observations
图选项

以理论固体潮 gthe(t′)为参考(理论固体潮时间长度是任意的)，前后移动短时间序列的整段重力观测数据gobs(t)，使得：

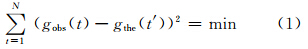
式中，N是重力观测数据的总个数。则移动的时间长度即为时间延迟Ts，根据Ts，将gobs(t)归算到时间历元t′上，即gobs(t′)，并建立其与gthe(t′)的线性关系：

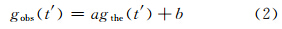
式中，a和b为待求参数，认为是尺度因子。根据最小二乘原理可得到a和b的估值为[18]：

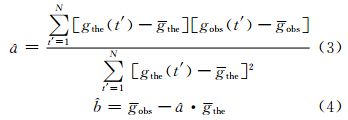
其中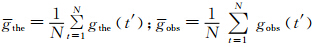，。由理论潮汐gthe(t′)、 和 可以计算出任意时间长度的重力观测数据gfit(t′)：

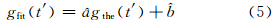
长时间序列重力数据gfit(t′)也可以表示为：

式中，δj和Hj是角频率为ωj分潮波的振幅因子和理论振幅；φj和Δφj是角频率为ωj分潮波的初始相位和相位延迟；d(t′ i)是仪器零漂；ε(t′ i)为数据中的各种观测误差。 采用Venedikov调和分析方法[19,20,21]求出各分潮波的振幅因子δj和相位延迟Δφj，再利用谐波法[22]计算潮汐改正量，最后结合时间延迟 Ts将潮汐改正量归算到短时间序列重力观测数据的时间历元t上，即实现短时间序列重力观测数据的潮汐改正。 2 数值计算与分析 2.1 采用的数据

没有长期连续潮汐观测站和现有的潮汐模型精度较低的地区一般是在海岛或海陆交界，由于这些地区没有实测重力观测数据，本文采用离海岸线最近的几个超导重力台站来验证该方法的有效性。国际大地测量与地球物理联合会的全球地球动力学项目(gobal godynamics poject,GGP)是从1997 年开始实施的，至今已有30多个台站(如图 2所示)，具有丰富的高精度重力观测资料，为验证TCMSSGO的正确性和有效性提供了良好的数据基础。本文计算选取了离海岸线最近的3个台站(图 2中已圈出)，分别为智利TIGO Concepcion、日本Kamioka和台湾Hsinchu台站，它们与海岸线的距离依次为11.83 m、32.52 m和7.82 m，现有潮汐模型的精度较低。

图 2 1997~2010年GGP台站的全球分布图Fig. 2 Global Dstribution of GGP Stations from 1997 to 2010
图选项
2.2 计算结果与分析 2.2.1 模型精度分析

图 3(a)为TIGO Concepcion台站2007年4月28日23:59:00至7月27日23:59:00的理论固体潮；图 3(b)中实线为2007年6月12日23:59:00至6月15日23:59：00三天的重力实测数据，虚线为TCMSSGO计算的长时间序列重力数据；图 3(c)是实际重力观测数据；图 3(d)为计算的长时间序列重力数据与实际观测数据之间的残差，标准差为3.885 6 μGal。

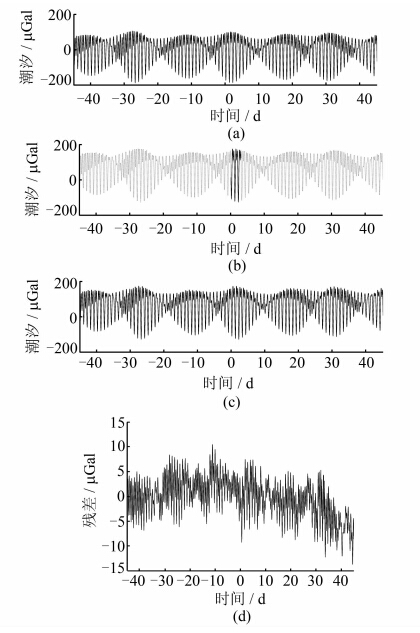图 3 TIGO Concepcion台站数据处理结果Fig. 3 Processing Results of TIGO Concepcion Station
图选项

由图 3(b)可知，在前后推估45 d范围内，计算的长时间序列重力数据精度整体上可以达到μGal量级，并且随着推估时间长度的增加，精度有缓慢降低的趋势。为研究TCMSSGO建立潮 汐模型的精度，利用Venedikov方法对计算的长 时间序列重力观测数据进行调和分析，考虑了M2、S2等11个主要周日和半日分潮波，并将其与真实重力观测数据建立的潮汐模型进行对比，其结果如表 1所示。表 1中,AF为振幅因子；PD为相位延迟(°)；Std为标准差；ΔAF为实际重力观测数据所建的潮汐模型中潮汐因子AF1和计算的长时间序列重力数据所建的潮汐模型中潮汐因子AF2的差值与AF1的比值，即ΔAF= |AF1-AF2 |/ AF1。

从表 1可以看出：①计算的长时间序列重力数据所建潮汐模型的振幅因子AF2的解算精度优于0.005，相位延迟PD2的解算精度优于0.3°(表 1中的加粗字体)，由文献[17]可知，TCMSSGO的潮汐改正精度可以达到μGal量级；②与真实模型差异ΔAF的最大值不超过0.056 51，说明TCMSSGO能够较准确地恢复各分潮波信号；③TCMSSGO建立潮汐模型的振幅因子和相位延迟解算精度均优于实际重力观测数据的建模结果，其原因可能是因为TCMSSGO在计算长时间序列数据之前进行了时间延迟改正，对相位延迟已经有所改善；线性拟合实际上是一次低通滤波过程，可以改善振幅因子解算的精度。

表 1 利用Venedikov方法对计算的长时间序列重力观测数据与真实重力观测数据的调和分析结果对比 Tab. 1 Results of Harmonic Analysis from Long Time Fitting Data and Gravity Observations by Venedikov
分潮波实际重力观测数据计算的长时间序列重力数据 ΔAF
AF1StdPD1/(°)Std/(°)AF2StdPD2/(°)Std/(°)
Q1 1.191 10 0.005 23 2.205 0.239 1.181 28 0.001 89 0.023 0.092 0.008 24
O1 1.192 90 0.000 89 1.680 0.044 1.182 39 0.000 33 0.000 0.016 0.008 81
NO1 1.205 31 0.009 36 1.303 0.453 1.192 06 0.003 49 0.264 0.169 0.010 99
K1 1.187 21 0.000 54 0.921 0.025 1.164 88 0.000 19 0.035 0.010 0.018 80
J1 1.187 85 0.010 19 -2.099 0.588 1.184 67 0.003 81 -0.004 0.216 0.002 67
OO1 1.169 27 0.012 58 0.322 0.626 1.164 13 0.004 72 0.373 0.234 0.004 39
2N2 1.261 95 0.006 30 -2.210 0.286 1.190 63 0.000 69 -0.076 0.033 0.056 51
N2 1.191 08 0.001 11 -2.793 0.054 1.190 25 0.000 12 -0.002 0.006 0.000 69
M2 1.150 57 0.000 20 -2.385 0.010 1.190 39 0.000 02 0.005 0.001 0.034 60
L2 1.165 10 0.005 03 -1.672 0.247 1.191 92 0.000 54 0.002 0.026 0.023 01
S2 1.129 15 0.000 50 -1.353 0.026 1.190 60 0.000 06 0.014 0.003 0.054 42
表选项

图 3(a)中三天的重力观测数据是选择在大潮附近，为探究TCMSSGO建立的潮汐模型与短时间序列重力观测数据的位置(大潮、低潮)关系，将三天的重力观测数据向右移动至低潮，如图 4(a)中的实线部分所示。图 4(a)中虚线部分为TCMSSGO计算的长时间序列重力数据，图 4(b)为计算的长时间序列重力数据与实际重力观测数据的残差，标准差为4.433 7 μGal。

由图 3(b)和图 4(b)可知，短时间序列重力观测数据在小潮比在大潮得到的长时间序列重力数据精度略低(4.433 7 μGal，大于3.885 6 μGal)。表 2为根据小潮附近三天的重力观测数据由TCMSSGO建立的潮汐模型。

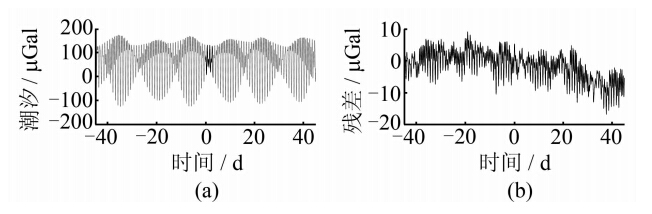图 4 重力观测数据在低潮时候的数据处理结果Fig. 4 Processing Results of Gravity Observations in Low Tide
图选项
表 2 根据小潮附近三天数据计算长时间重力数据的调和分析结果 Tab. 2 Results of Harmonic Analysis from Long Time Fitting Data Based on Neap in Three Days
分潮波计算的长时间序列重力观测数据ΔAF
AF2StdPD2/(°)Std/(°)
Q1 1.171 25 0.001 88 0.054 0.092 0.016 66
O1 1.171 54 0.000 32 0.001 0.016 0.017 90
NO1 1.165 48 0.003 58 0.349 0.175 0.033 04
K1 1.154 19 0.000 19 0.004 0.009 0.027 81
J1 1.172 21 0.004 74 0.043 0.180 0.013 16
OO1 1.180 15 0.004 60 -0.865 0.222 0.009 30
2N2 1.180 36 0.000 75 -0.054 0.037 0.064 65
N2 1.179 36 0.000 12 0.004 0.006 0.009 83
M2 1.179 43 0.000 02 0.007 0.001 0.025 08
L2 1.180 32 0.000 56 0.031 0.027 0.013 06
S2 1.179 73 0.000 06 0.016 0.003 0.044 79
表选项

在表 2中，ΔAF的最大值为2N2分潮波的0.064 65，比表 1中的0.056 51略高，其他各分潮也基本有类似的现象。由表 1和表 2可以看出，与实际重力观测数据建立的潮汐模型相比，观 测数据在大潮位置获取的振幅因子衰减比观测数据在低潮时小，更接近真实潮汐模型。Kamioka和Hsinchu台站的处理结果具有相同的现象，因此建议重力实测数据的采集时间应选择在大潮附近，以便采用TCMSSGO进行潮汐改正。 2.2.2 时间有效性分析

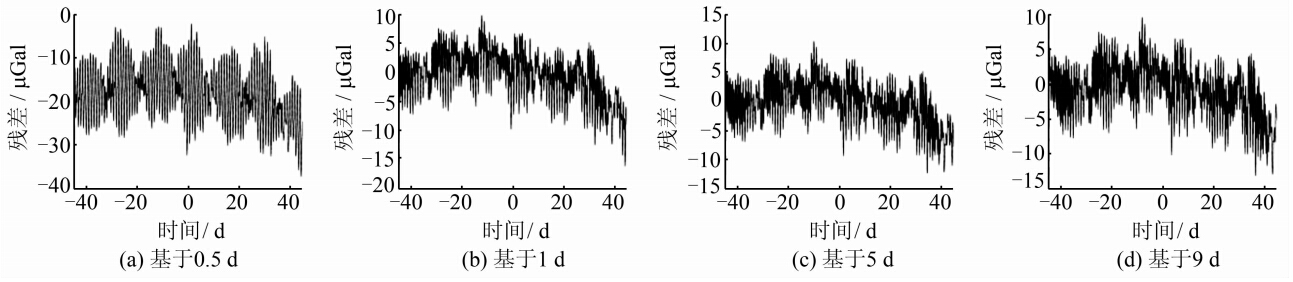
为探究实际观测数据的长度与潮汐模型精度之间的关系，本文分别采用时间长度为0.5 d、1 d、5 d和9 d的实际重力观测数据(起始时间为2007年6月12日23:59:00)，利用TCMSSGO计算出2007年4月28日23:59:00至7月27日23:59:00的重力数据，并与真实重力观测数据比较，其结果如图 5所示。图 5(a) 、5(b)、5(c)和5(d)分别是基于0.5 d、1 d、5 d和9 d实际观测数据的计算结果与实际重力观测数据的残差，标准差分别为5.999 9 μGal、4.015 9 μGal、3.788 5 μGal和3.712 2 μGal。

图 5 不同时间长度观测数据的拟合结果与实际观测数据的残差Fig. 5 Residuals Between Fitting Results and Observations from Gravity Observations in Different Days
图选项

由图 5可知，在前后推估45天范围内，基于0.5 d实际观测数据计算的长时间序列重力数据的精度较差，标准差为5.999 9 μGal，并存在约20 μGal的系统误差；1 d实际观测数据的计算结果精度有所改善，标准差为4.015 9 μGal，5~9 d实际观测数据的计算结果精度在逐渐提高，整体上均可以达到μGal量级。综合分析图 3和图 5可 知，随着观测数据长度的增加，计算的长时间序列 重力数据的精度在缓慢提高，建议采用TCMSSGO进行潮汐改正时，观测数据的时间长度应多于1 d。 2.2.3 空间有效性分析

为验证TCMSSGO的空间有效性，本文选用了Kamioka和Hsinchu台站大潮附近两天的重力观测数据进行处理，建立潮汐模型，并与实际重力观测数据进行对比，其结果如表 3和表 4所示。

表 3 Kamioka台站调和分析结果 Tab. 3 Results of Harmonic Analysis at Kamioka Station
分潮波实际重力观测数据拟合重力数据ΔAF
AF1StdPD1/(°)Std/(°)AF2StdPD2/(°)Std/(°)
Q1 1.196 61 0.005 98 0.941 0.282 1.188 72 0.002 32 0.110 0.111 0.006 59
O1 1.200 30 0.001 11 0.696 0.052 1.188 45 0.000 44 0.010 0.020 0.009 87
NO1 1.158 46 0.018 56 -0.936 0.925 1.194 68 0.007 28 -0.368 0.350 0.031 26
K1 1.180 68 0.000 79 -0.371 0.041 1.169 29 0.000 31 -0.178 0.016 0.009 64
J1 1.159 16 0.012 17 -0.217 0.598 1.190 93 0.004 76 -0.365 0.231 0.027 40
OO1 1.180 34 0.016 61 -2.346 0.797 1.186 16 0.006 45 0.264 0.305 0.004 93
2N2 1.186 21 0.005 93 0.168 0.286 1.196 32 0.000 60 -0.022 0.029 0.008 52
N2 1.186 88 0.001 15 0.189 0.055 1.196 33 0.000 11 0.014 0.005 0.007 96
M2 1.190 11 0.000 24 0.452 0.012 1.196 37 0.000 02 0.009 0.001 0.005 26
L2 1.213 90 0.010 74 -0.239 0.511 1.191 79 0.001 08 -0.075 0.052 0.018 21
S2 1.201 73 0.000 39 -0.008 0.019 1.196 62 0.000 04 0.014 0.002 0.004 25
表选项
表 4 Hsinchu台站调和分析结果 Tab. 4 Results of Harmonic Analysis at Hsinchu Station
分潮波实际重力观测数据拟合重力数据ΔAF
AF1StdPD1/(°)Std/(°)AF2StdPD2/(°)Std/(°)
Q1 1.265 72 0.004 65 -1.720 0.212 1.186 66 0.001 85 -0.001 0.090 0.062 46
O1 1.238 55 0.000 94 -2.287 0.043 1.187 31 0.000 37 0.006 0.018 0.041 37
NO1 1.224 01 0.015 37 -2.544 0.722 1.222 88 0.006 01 0.442 0.280 0.000 92
K1 1.186 71 0.000 54 -2.818 0.027 1.168 92 0.000 22 -0.056 0.011 0.014 99
J1 1.198 10 0.008 90 -3.800 0.527 1.187 18 0.003 54 0.008 0.205 0.009 11
OO1 1.168 68 0.016 27 -2.432 0.816 1.217 71 0.006 47 0.704 0.302 0.041 95
2N2 1.170 61 0.004 90 -0.012 0.240 1.194 67 0.000 22 -0.006 0.011 0.020 55
N2 1.189 93 0.001 11 -3.330 0.053 1.194 52 0.000 05 0.008 0.002 0.003 85
M2 1.160 31 0.000 25 -2.972 0.012 1.194 47 0.000 01 0.005 0.001 0.029 44
L2 1.173 68 0.007 82 -1.570 0.416 1.192 84 0.000 35 -0.012 0.017 0.016 32
S2 1.158 56 0.000 62 -1.310 0.031 1.194 47 0.000 03 0.007 0.001 0.030 99
表选项

由表 3和表 4可知，基于Kamioka台站的重力观测数据，采用TCMSSGO建立的潮汐模型，振幅因子解算的精度优于0.008，相位延迟解算的精度优于0.35°，与真实模型的差异ΔAF 优于0.031 26(表 3中加粗字体)；Hsinchu台站建立的潮汐模型的振幅因子解算的精度优于0.007， 相位延迟解算的精度优于0.35°，ΔAF优于0.062 46(表 4中加粗字体)。因此，Kamioka和Hsinchu台站建立的潮汐模型的精度均可以达到μGal量级，说明TCMSSGO在全球分布的3个不同台站均适用，初步验证了该方法的空间有效性。 3 结 语

本文系统研究了基于短时间序列重力观测数据的潮汐改正方法，并采用三个海陆交界位置的超导重力台站观测数据进行了试验分析和验证。

1) 基于三个不同位置的超导重力台站，利用TCMSSGO建立的潮汐模型的振幅因子解算的精度均优于0.01，相位延迟解算精度优于0.5°，说明TCMSSGO的潮汐改正可以达到μGal量级，验证了该方法的正确性和有效性。

2) 对于同一个观测台站，随着观测数据长度的增加，重力残差在逐渐减小，但为了使TCMSSGO潮汐改正精度达到μGal量级，建议短时间序列重力观测数据的长度不少于1 d。

3) 为尽量减少振幅因子的衰减幅度，应采用大潮附近的短时间序列重力观测数据来计算长时间序列重力数据，构建潮汐模型，实施潮汐改正。

参考文献
[1] Melchior P, Francis O. Tidal Loading in the Caribbean Sea, as Measured Along the Central America and South America Coasts[J]. Wolfgang Torgés Festschrift, Wissenschatf tliche Arbeiten der Fachrichtung Vermessungswesen derUniversitt Hannover, 2001, 241:25-41
[2] Wang Yong, Zhang Weiming, Wang Hubiao, et al. Tide Correction of Absolute Gravity Measurements[J]. Journal of Geodesy and Geodynamics, 2003, 23(2):65-68(王勇, 张为民, 王虎彪, 周旭华. 绝对重力观测的潮汐改正[J]. 大地测量与地球动力学, 2003, 23(2):65-68)
[3] Xu J Q, Sun H P, Yang X F. A Study of Gravity Variations Caused by Polar Motion Using Superconducting Gravimeter Data from the GGP Network[J]. Journal of Geodesy, 2004, 78(3):201-209
[4] Ducarme B, Timofeev V Y, Everaerts M, et al. A Trans-Siberian Tidal Gravity Profile (TSP) for the Validation of the Ocean Tides Loading Corrections[J]. Journal of Geodynamics, 2008, 45(2):73-82
[5] Neumeyer J, del Pino J, Dierks O, et al. Improvement of Ocean Loading Correction on Gravity Data with Additional Tide Gauge Measurements[J]. Journal of Geodynamics, 2005, 40(1):104-111
[6] Zhou X H, Wu B, Zhu Y Z, et al. The Ocean Tidal Displacement Corrections for Earth Crust Movement Network of China[J]. Chinese Astronomy and Astrophysics, 2002, 26(1):81-87
[7] Zhou Jiangcun, Sun Heping. Synthetic Tidal Parameters for Gravity over China and Its Neighbor Area[J]. Acta Seismologica Sinica, 2007, 29(6):618-624(周江存, 孙和平. 中国及邻区重力合成潮汐参数[J]. 地震学报, 2007, 29(6):618-624)
[8] Sun Heping, Xu Houze, Luo Shaocong, et al. Study of the Ocean Models Using Tidal Gravity Observations Obtained with Superconducting Gravimeter[J]. Acta Geodaetica et Cartographica Sinica, 1999, 28(2):115-120(孙和平, 许厚泽, 罗少聪, 等. 用超导重力仪的潮汐观测资料研究海潮模型[J]. 测绘学报, 1999, 28(2):115-120)
[9] Song Xingli, Yu Chen. Gravity Tide Corrections[J]. Chinese Journal of Geophysics, 1988, 31(5):519-526(宋兴黎, 于沉. 重力潮汐改正[J]. 地球物理学报, 1988, 31(5):519-526)
[10] Li Ruihao, Sun Heping, Chen Dongsheng, et al. On the Correction to Observation of Gravity Tides and the Indication of Gravity Anomaly[J]. Acta Seismologica Sinica, 1991, 13(2):259-269(李瑞浩, 孙和平, 陈冬生, 等. 重力潮汐观测资料的改正和异常背景值的显示问题[J]. 地震学报, 1991, 13(2):259-269)
[11] Li Jianguo, Zhang Hongwei, Wang Yingjian, et al.The Adjustment of the Earth Tide in Gravimetric Calculation[J]. Beijing Surveying and Mapping, 2012(5):1-5(李建国, 张宏伟, 王应建, 等. 重力计算中的潮汐改正分析[J]. 北京测绘, 2012(5):1-5)
[12] Zahran K H, Jentzsch G, Seeber G. World-wide Synthetic Tide Parameters for Gravity and Vertical and Horizontal Displacements[J]. Journal of Geodesy, 2005, 79(6/7):293-299
[13] Sun Heping, Xu Houze, Zhou Jiangcun, et al. Latest Observation Results from Superconducting Gravimeter at Station Wuhan and Investigation of the Ocean Tide Models[J]. Chinese Journal of Geophysics, 2005, 48(2):299-307(孙和平, 许厚泽, 周江存, 等. 武汉超导重力仪观测最新结果和海潮模型研究[J]. 地球物理学报, 2005, 48(2):299-307)
[14] Xu Houze.Tide Corrections of Precise Gravity Measurments[J]. Acta Geodaetica et Cartographica Sinica, 1984, 13(2):88-93(许厚泽. 精密重力测量的潮汐改正[J]. 测绘学报, 1984, 13(2):88-93)
[15] Zhou J C, Ducarme B, Sun H P. Validating the Synthetic Tidal Parameters of Gravity with Superconducting Gravimetric Observations[J]. Bull Inf Marées Terrestres, 2007, 143:11 489-11 497
[16] Zhang Hongwei, Zhang Songtang, Xiao Fan, et al.Effect of Tides on Relative Gravity Survey of Ocean Islands[J]. Journal of Geomatics, 2012, 37(1):43-45(张宏伟, 张松堂, 肖凡, 等. 海岛礁相对重力测量的潮汐影响[J]. 测绘信息与工程, 2012, 37(1):43-45)
[17] Cartwright D E, Tayler R J. New Computations of the Tide-generating Potential[J]. Geophys J, 1971, 23:45-74
[18] Chen Xiaodong.Detection and Investigation of the Gravity Pole Tide by Using the Global Superconducting Gravity Observation Technique[D]. Wuhan:Institute of Geodesy and Geophysics, Chinese Academy of Sciences, 2010(陈晓东. 利用全球超导重力观测技术检测和研究重力极潮[D]. 武汉:中国科学院测量与地球物理研究所, 2010)
[19] Chen Xiaodong.Preprocessing and Analytical Results of the Tidal Gravity Observations Recorded with a Superconducting Gravimeter at Jiufeng Station, Wuhan[D]. Wuhan:Institute of Geodesy and Geophysics, Chinese Academy of Sciences, 2003(陈晓东. 武汉九峰台超导重力仪固体潮观测资料的预处理和分析结果[D]. 武汉:中国科学院测量与地球物理研究所, 2003)
[20] Tian Guie, Sun Heping, Chen Xiaodong. Determination of Long Period Gravity Tide Parameter at Wuhan Station[J]. Journal of Geodesy and Geodynamics, 2005, 25(4):99-104(田桂娥, 孙和平, 陈晓东. 武汉重力固体潮长周期潮汐参数的确定[J]. 大地测量与地球动力学, 2005, 25(4):99-104)
[21] Tong Zhanglong.Investgation on Methods and Application for the Harmonic Analysis of Tides[D]. Nanjing:Hohai University, 2007(童章龙. 潮汐调和分析的方法和应用研究[D]. 南京:河海大学, 2007)
[22] Xu Jianqiao, Sun Heping, Luo Shaocong. Determination of the Synthetic Gravity Tides at Wuhan Fundamental Station[J]. Crustal Deformation and Earthquake, 1999, 19(3):26-31(徐建桥, 孙和平, 罗少聪. 武汉基准台重力合成潮信号确定[J]. 地壳形变与地震, 1999, 19(3):26-31)