文章信息
- 杨曦光, 黄海军, 严立文, 刘艳霞, 马立杰
- YANG Xiguang, HUANG Haijun, YAN Liwen, LIU Yanxia, MA Lijie
- 近岸水体表层悬浮泥沙平均粒径遥感反演
- Average Grain Size Inversion of Suspended Sediment in Offshore Waters
- 武汉大学学报·信息科学版, 2015, 40(2): 164-169
- Geomatics and Information Science of Wuhan University, 2015, 40(2): 164-169
- http://dx.doi.org/10.13203/j.whugis20130057
-
文章历史
- 收稿日期:2013-04-19
2. 中国科学院大学, 北京 100049;
3. 中国科学院海洋地质与环境重点实验室, 山东 青岛 266071
2. University of the Chinese Academy of Sciences, Beijing 100049, China;
3. Key Laboratory of Marine Geology and Environment, Institute of Oceanology, Chinese Academy of Sciences, Qingdao 266071, China
悬浮泥沙的粒径大小及分布特征不仅体现了海域水体中颗粒态物质的存在状态,而且悬浮泥沙级配(或粒径组成)和悬沙浓度可以指示水动力及再悬浮作用的过程和强度[1]。常规的海水悬浮物平均粒径数据是通过走航取样、实验室分析获取,大区域的粒径分布特征也是通过调查数据空间插值获取,在调查速度和周期上,都很难满足大面积调查的要求[2],对于水动力作用强烈的地区,很难捕获瞬时海水表层悬浮泥沙的粒径分布特征。遥感技术为快速、定量地获取区域环境参数提供了参考。Rainey 等人[3]利用图像处理技术从机载ATM(airborne thematic mapper)上获取了潮间带地区的沉积物粒径分布特征,结果表明,遥感技术可以应用到更广泛的河口地区调查研究中。Kostadinov 等人[4]结合Mie散射理论,利用查找表的方法,对全球海洋的悬浮物粒径分布特征进行了讨论。Huang等人[5]利用不同类型的遥感数据反演潮间带底质平均粒径,并对多光谱和高光谱遥感数据的反演结果进行了比较分析[5]。Chakraborty等[6]利用声学后向散射数据和神经网络模型反演海底沉积物类型,结果表明,BP神经网络反演的平均粒径与实测结果具有很好的一致性。目前,关于粒径分布特征的研究主要集中在潮间带,而对表层海水的悬浮物粒径分布特征的研究较少。本文尝试利用Mie理论,结合海洋光学原理建立了基于表层海水固有光学参数的悬浮泥沙平均粒径的遥感反演模型。相关研究不仅缩短了调查周期,降低了调查成本,而且避免了大区域平均粒径空间插值带来的不确定性,相关信息可以为深入开展陆海相互作用、海洋生态系统演变以及海洋参与全球碳循环等研究提供数据支持。
1 研究区域及泥沙粒径数据采集方法 1.1 研究区域
黑泥湾位于山东半岛东侧,地处E 122°31′~122°37′,N 36°55′~37°2′。北部隔楮岛半岛与桑沟湾相邻,南部隔镆铘岛与石岛湾相邻,海湾湾口开阔,中部岸线向外突出,将海湾分成南北两部分。黑泥湾水下地形较为平缓,水动力作用单一,湾内基本无河流注入。
1.2 数据采集
数据采集时间为2004年11月,共设置25个站位。海水的样品采集严格按照GB/T13909-92海洋调查规范进行,采用负压抽滤法抽滤,滤膜为0.45 μm的聚酯纤维膜,并按照20%设置校正膜。海水过滤后,用蒸馏水冲洗量筒一次,滤膜洗盐三次。
滤膜放入烘箱,用40 ℃恒温烘干8 h,之后放入干燥皿中,使之恢复常温,用万分之一电子天平称重。称重后,将滤膜再次烘干4 h,放入干燥皿,待常温后再次称重。反复上述步骤,直至每张滤膜前后两次称重误差在0.01 mg之内。
将称重合格的滤膜(含悬浮物)放入预先烘烧称重的坩埚中,先用酒精灯将滤膜燃烧,然后在500 ℃下烘烧1 h,除去有机物质,然后反复烘干、干燥冷却与称重,直至前后两次称重误差在0.01 mg以内[7]。最后,利用Cilas940L型激光粒度仪(测量粒径范围为0.38~2 000 μm)对悬浮泥沙样品粒度进行测试。
2 原理与方法 2.1 平均粒径反演模型
MIE理论中,后向散射效率因子 Qbb可以描述均匀球形颗粒的后向散射特征,其数学表达式为[8]:
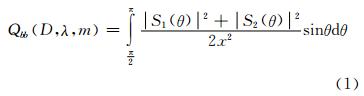
式中,S1(θ)和S2(θ)称为振幅函数,它是球形颗粒直径D、入射光波长λ以及颗粒复折射指数m的函数,其表达式及计算方法可参阅文献[9];x为尺度参数,定义为x=2πD/λ,代表颗粒周长与入射波长的比值;θ为散射角;m=n+in′为颗粒的复折射指数,其实部n表示颗粒的折射,虚部n′表示颗粒的吸收;海水中的悬浮物其复折射指数中实部n介于1.01~1.21之间,有机组分n介于1.02~1.08,而无机组分n介于1.15~1.20之间;虚部n′介于0~0.01之间[10];Qbb描述了单个颗粒对光的散射能力,通过它可以进一步计算颗粒群的后向散射系数[11]。
假设悬浮泥沙颗粒为均质球形粒子,在波长λ处,单位体积内的后向散射系数bbX(λ)可表示为[4]:
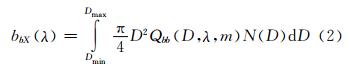
式中,N(D)为悬浮泥沙颗粒尺度分布函数,描述单位体积内直径为D的颗粒的数量,可表示为:
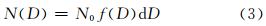
f(D)为粒径分布频率,可通过Cilas940L型激光粒度仪直接测得;N0是参考单位体积颗粒数,可通过悬浮泥沙浓度和密度估算,

式中,CX为悬浮泥沙含量;ρX为沙的密度。
将悬浮泥沙平均粒径D引入到N0的计算中,则式(4)可写成:
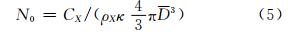
式中,κ为统计意义上的修正系数。将式(5)、式(3)代入式(2),得到含有平均粒径 的悬浮泥沙后向散射系数bbX(λ)的表达式:
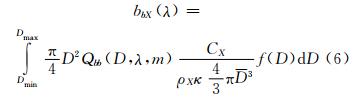
整理得:
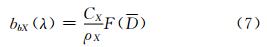
对于实际测量站位,其悬浮泥沙浓度、粒径的分布特征及颗粒物直径的极值是已知的,利用MIE理论,可以计算出每个站位的后向散射效率因子 Qbb及悬浮泥沙的后向散射系数bbX,将计算的Qbb及bbX作为数据样本集,拟合bbX与平均粒径D的函数关系,可以建立基于水体固有光学参数表层悬浮泥沙平均粒径反演模型。结合同步遥感数据,实现利用少量的测量数据反演大区域表层海水悬浮泥沙的平均粒径。
2.2 悬浮泥沙后向散射系数的估算
近岸及河口区等典型二类水体的后向散射特征可以用纯水、叶绿素和悬浮泥沙的含量及其吸收/散射系数的函数来描述[12]:
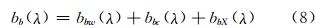
即总后向散射系数bb为纯水后向散射系数(bbw)、浮游植物后向散射系数(bbc)和悬浮泥沙后向散射系数(bbX)之和。因此,悬浮泥沙后向散射系数bbX可表示为:
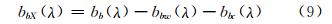
式中,bbw可通过式(10)计算出[13]:

bw(500)为纯水在500 nm的散射系数,其值为0.002 88 m-1。bbc可表示为[14]:
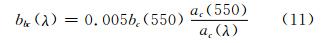
bc(550)=0.12Cc0.63,为550 nm处叶绿素的散射系数;ac(λ)为叶绿素的吸收系数。
因此,在已知总后向散射系数bb的前提下,可以求解出悬浮泥沙的后向散射系数bbX。
QAA(quasi-analytical algorithm)是一种计算水色要素的吸收和后向散射特征的多波段半分析算法。利用QAA算法反演总后向散射系数及叶绿素吸收系数,从而可以推算出悬浮泥沙后向散射系数,再结合平均粒径反演模型,就可以反演出研究海域成像瞬时表层海水悬浮泥沙平均粒径的分布特征。QAA算法描述及本地化参数设置可参阅文献[15]。 3 反演模型及分析 3.1 后向散射效率因子随粒径的变化规律
参考激光粒度仪的测量范围及实际样品两个因素,确定颗粒的大小取值为0.4~100 μm。利用Mie理论计算特定波长处不同颗粒的后向散射特征。
入射光440 nm处,不考虑吸收情况,不同折射指数单球形颗粒后向散射特征如图 1(a)所示。随着颗粒直径的增加,后向散射效率因子 Qbb呈现振荡变大的趋势;复折射指数变化,Qbb随着颗粒粒径变化的规律基本保持不变。对于某一固定大小的颗粒,复折射指数增加,Qbb整体变小。在考虑吸收特征时,单球形颗粒后向散射特征随颗粒粒径变化的规律大致相同 (见图 1(b))。复折射指数实部n不变,直径小于10 μm颗粒的后向散射效率因子Qbb随着虚部n′ 的增大而减小,而直径大于10 μm颗粒的后向散射效率因子增大。通过计算其他波段的后向散射特征,亦发现相似的变化规律。

|
| 图 1 后向散射效率因子随粒径变化特征 Fig. 1 Variation Characteristic of Backscattering Efficient Factor at Different Grain Size |
根据式(2)计算所有站位的悬浮泥沙后向散射系数。参考式(7),利用线性函数、指数函数、幂函数等形式拟合悬浮泥沙后向散射系数和平均粒径的函数 bbX(λ)=F(D)。结果表明,Mie理论计算采样站位的bbX(λ)与对应的平均粒径 的三次方线性关系明显(见图 2)。其线性方程的通用形式为:

|
| 图 2 MIE计算的悬浮泥沙后向散射系数与平均粒径三次方的散点图(中间线为拟合曲线,两侧线为95%置信区间) Fig. 2 Scattering Diagram Between Estimated Suspended Sediment Back Scattering Coefficient and Cubic Average Grain Size |

其中,沙密度取值为2 600 kg/m3。考虑到变量数量级及K的统计特征,本文没有对变量进行单位换算。
按照3∶1的比例将数据分成两部分,其中17个站位用于拟合系数K,剩余8个站位数据用于模型精度验证。拟合得到MODIS几个水色波段(412 nm、443 nm、555 nm、667 nm)悬浮泥沙平均粒径反演模型及精度如表 1所示。
| 波段/nm | 模型 | 决定系数 | 拟合误差/% | 拟合RMSE/m-1 | 检验误差/% | 检验RMSE/m-1 |
| 412 |
bbX(λ)=0.001 1 D3-0.007 3 D3-0.007 3 | 0.931 6 | 16.632 2 | 0.024 2 | 23.680 0 | 0.066 4 |
| 443 |
bbX(λ)=0.009 D3-0.007 D3-0.007 | 0.932 7 | 17.607 5 | 0.018 7 | 25.550 2 | 0.055 1 |
| 555 |
bbX(λ)=0.000 4 D3-0.004 5 D3-0.004 5 | 0.933 8 | 18.953 7 | 0.008 8 | 24.701 8 | 0.024 8 |
| 667 |
bbX(λ)=0.000 2 D3-0.002 7 D3-0.002 7 | 0.933 6 | 20.314 3 | 0.004 8 | 24.533 9 | 0.012 9 |
要获取表层悬浮泥沙平均粒径,不仅需要表层海水中悬浮泥沙的后向散射系数,还需要表层悬浮泥沙的浓度作为辅助数据才能实现悬浮泥沙平均粒径的反演。从MODIS影像上获取遥感反射率与对应站位的悬浮泥沙浓度,建立表层悬浮泥沙反演统计模型。分析发现,MODIS 555 nm遥感反射率与悬浮泥沙浓度的对数线性关系最好,建模样本为17个,剩余8个样本用来检验。建立的模型为:
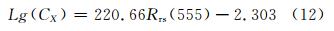
模型决定系数为0.706 6,模型拟合平均误差为6.245 3%,拟合RMSE为0.083 7,模型检验平均误差为14.758 8%,检验样本RMSE为0.231 6。
3.4 反演结果的比较与分析
利用MODIS遥感反射率产品(MODIS-Rrs),结合QAA后向散射系数反演算法,计算对应站位的悬浮泥沙后向散射系数,并与Mie理论模拟结果进行比较,见图 3。从图 3可以看出,两结果之间存在一定的线性关系,通过对比QAA算法推算的悬浮泥沙后向散射系数与Mie理论模拟结果发现,QAA算法估算的悬浮泥沙后向散射系数结果偏高,并且QAA算法计算的结果呈现出在一定区间内聚集的现象。其可能原因是由于MODIS遥感反射率产品大气校正误差、QAA算法中经验参数的不适应以及空间尺度问题引起的。

|
| 图 3 MIE模拟的悬浮泥沙后向散射系数与MODIS QAA计算结果的比较 Fig. 3 Comparison of Calculated the Suspended Sediment Backscattering Coefficient Between MIE Theory and MODIS QAA Algorithm |
利用QAA算法和悬浮泥沙浓度模型,从MODIS影像上获取研究区域的悬浮泥沙后向散射系数和悬浮泥沙浓度,并结合平均粒径反演算法反演研究区表层海水悬浮泥沙平均粒径,其结果如图 4(c)所示。通过对比MODIS反演的悬浮泥沙平均粒径与实测数据,在412 nm处,其平均相对误差为20.096 1%,均方根误差为6.160 3 μm;443 nm处,其平均相对误差为22.387 6%,均方根误差为7.154 8 μm;555 nm处,平均相对误差为23.026 6%,均方根误差为6.233 8 μm;667 nm处,其平均相对误差为44.164 5%,均方根误差为2.899 4 μm。在近岸高悬浮泥沙区域,其结果与实际调查结果相一致,吻合较好。离岸较远的水体,其成分主要以叶绿素及浮游植物碎屑为主,泥沙含量极少,悬浮泥沙不再是水体光学特征的主控因素,水体后向散射系数主要是由于藻类及浮游植物碎屑颗粒引起的,本文模型中悬浮泥沙浓度和密度参数不适用于以藻类和浮游植物碎屑为主的水域。
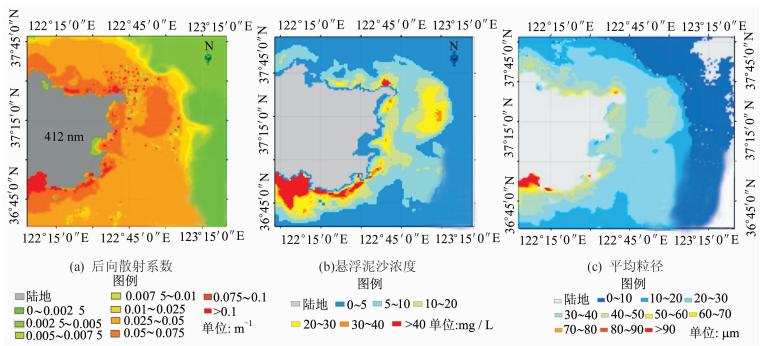
|
| 图 4 反演的悬浮泥沙后向散射系数、悬浮泥沙浓度和平均粒径 Fig. 4 Retrieval of Suspended Sediment Backscattering Coefficient ,Concentration of Suspended Sediment and Average Grain Size |
本文结合Mie理论和海洋光学原理,建立了海水表层悬浮泥沙平均粒径的遥感反演方程。利用Mie理论模拟了直径为D的球形颗粒的后向散射效率因子,讨论了颗粒后向散射效率因子的变化特征 和规律。通过后向散射效率因子推算悬浮泥沙粒子群的后向散射系数,并拟合悬浮泥沙后向散射系数与粒子群平均粒径的函数关系。结果表明,悬浮泥沙后向散射系数与其平均粒径的三次方正相关,线性关系明显,拟合方程决定系数均在0.93以上。 近岸高悬浮泥沙区域的反演结果与实测数据吻合较好,能够反映海水表层悬浮泥沙的平均粒径分布特征,为相关研究提供数据参考。
本研究中,MIE理论计算后向散射系数过程中没有考虑到悬浮物物质组成对其后向散射特征的影响,因此,提高模型精度及其适用范围,以及改进QAA算法,以提高其后向散射系数的估算精度,有待进一步研究。
致谢:感谢武汉大学黄珏同学在海洋光学原理方面提供的帮助以及NASA提供的MODIS数据产品。
| [1] | Li Zhanhai, Chen Shenliang, Zhang Guoan. The Study on Grain-Size Distribution of Suspended Sediment and Resuspension Process on the Chongming East Intertidal and Subtidal Zones in the Changjiang Estuary in China[J]. Acta Oceanologica Sinica, 2008, 30(6):154-163(李占海, 陈沈良, 张国安.长江口崇明东滩水域悬沙粒径组成和再悬浮作用特征[J].海洋学报, 2008, 30(6):154-163) |
| [2] | Liu Zhonghua, Li Yunmei, Lv Heng, et al. Inversion of Suspended Matter Concentration in Lake Chaohu Based on Partial Least-squares Regression[J]. Journal of Lake Sciences, 2011, 23(3):357-365(刘忠华, 李云梅, 吕恒, 等.基于偏最小二乘法的巢湖悬浮物浓度反演[J].湖泊科学, 2011, 23(3):357-365) |
| [3] | Rainey M P, Tyler A, Gilvear D, et al. Mapping Intertidal Estuarine Sediment Grain Size Distributions Through Airborne Remote Sensing[J]. Remote Sensing of Environment, 2003, 86(4):480-490 |
| [4] | Kostadinov T S, Siegel D A, Maritorenas S. Retrieval of the Particle Size Distribution from Satellite Ocean Color Observations[J]. Journal of Geophysical Research:Oceans, 2009, 114(C9):C09015 |
| [5] | Huang Haijun, Liu Yanxia, Wang Bo. Effect of Spatial and Spectral Resolution of Images on Interperting Intertidal Estuarine Sediment Grain Size Distributions[C]. 2010 30th IEEE International Geoscience and Remote Sensing Symposium, Piscataway, 2010 |
| [6] | De Chakraborty B C. Estimation of Mean Grain Size of Seafloor Sediments Using Neural Network[J]. Marine Geophysical Research, 2012, 33(1):45-53 |
| [7] | Fan Hui, Huang Haijun. Remote Sensing Retrieval of Suspended Particulate Matter Concentrations of Surface Waters Near Radial Sand Ridges Area in the South Yellow Sea[J]. Scientia Geographica Sinica, 2011, 31(2):159-165 (樊辉, 黄海军. 南黄海辐射沙洲邻近海域表层悬浮颗粒物浓度遥感反演[J].地理科学, 2011, 31(2):159-165) |
| [8] | Zhou Wen, Cao Wenxi, Li Cai. Modeling Absorption and Scattering Properties of Mineral Particles Suspended in Seawater Based on Mie Theory[J]. Journal of Tropical Oceanography, 2008, 27(1):22-26(周雯, 曹文熙, 李彩.海水中矿物质颗粒吸收和散射特性Mie理论分析[J]. 热带海洋学报, 2008, 27(1):22-26) |
| [9] | Boss E, Twardowski M S, Herring S. Shape of the Particulate Beam Attenuation Spectrum and Its Inversion to Obtain the Shape of the Particulate Size Distribution[J]. Applied Optics, 2001, 40(27):4 885-4 893 |
| [10] | Babin M, Morel A, FournierR-Sicre V, et al. Light Scattering Properties of Marine Particles in Coastal and Open Ocean Waters as Related to the Particle Mass Concentration[J]. Limnology and Oceanography, 2003, 48(2):843-859 |
| [11] | Bricaud A, Morel A. Light Attenuation and Scattering by Phytoplanktonic Cells:A Theoretical Modeling[J]. Applied Optics, 1986, 25(4):571-580 |
| [12] | Smith R C, Baker K S. Optical Properties of the Clearest Natural Waters(200-800 nm)[J]. Applied Optics, 1981, 20(2):177-184 |
| [13] | Sathyendranath S, Prieur L, Morel A. A Three-Component Model of Ocean Colour and Its Application to Remote Sensing of Phytoplankton Pigments in Coastal Waters[J]. International Journal of Remote Sensing, 1989, 10(8):1 373-1 394 |
| [14] | Ahn Y H, Bricaud A, Morel A. Light Backscattering Efficiency and Related Properties of Some Phytoplankters[J]. Deep Sea Research Part A, 1992, 39(11/12):1 835-1 855 |
| [15] | Qing S, Tang J, Cui T, et al. Retrieval of Inherent Optical Properties of the Yellow Sea and East China Sea Using a Quasi-analytical Algorithm[J]. Chinese Journal of Oceanology and Limnology, 2011, 29(1):33-45 |
 2015, Vol. 40
2015, Vol. 40



