文章信息
- 王峰, 尤红建, 傅兴玉
- WANG Feng, YOU Hongjian, FU Xingyu
- 应用于SAR图像配准的自适应SIFT特征均匀分布算法
- Auto-Adaptive Well-Distributed Scale-Invariant Feature for SAR Images Registration
- 武汉大学学报·信息科学版, 2015, 40(2): 159-163
- Geomatics and Information Science of Wuhan University, 2015, 40(2): 159-163
- http://dx.doi.org/10.13203/j.whugis20130064
-
文章历史
- 收稿日期:2013-04-22
2. 中国科学院电子学研究所, 北京 100190;
3. 中国科学院大学, 北京 100049
2. Institute of Electronics, Chinese Academy of Science, Beijing 100190, China;
3. University of Chinese Academy of Science, Beijing 100049, China
遥感影像配准是遥感影像信息融合的重要前提,均匀分布的匹配点能保证图像配准的质量[1, 2]。由几何原理分析,对于配准中常用的线性几何变换模型,要求控制点离散分布,增加控制点的空间差异性,减少邻近控制点之间的影响,保证基于控制点的几何精矫正的精度。SIFT(scale invariant feature transform)是一种广泛使用的自动提取同名点的算法[3],由于SAR图像数据具有成像区域大、噪声干扰以及局部畸变严重等特点,提取的同名点会出现分布不均匀的问题。
为了控制SIFT同名点合理分布,Song等采用非极大值抑制NMS(non-maximal suppression)算法代替原始SIFT算法中的极值点检测策略[1];Lingua等在高斯尺度空间中运用双模板计算兴趣点局部纹理,确定兴趣点的对比度阈值[4];Sedaghat等提出一种UR-SIFT算法,首先确定特征点在尺度空间内的分布,然后通过计算图像内极值点的数目、对比度均值和熵均值自适应控制不同区域中SIFT特征点的数目[2],是一种较好的控制SIFT特征均匀分布的算法。但是UR-SIFT算法是针对成像质量好、噪声干扰小的光学遥感数据设计的,应用于SAR数据处理会提取出大量不稳定特征点,且提取的同名点分布不均匀。
本文针对SAR数据的特点,提出了一种双自适应稳定SIFT算法(double adapted stable SIFT,DAS-SIFT),推导出特征点在尺度空间和图像空间的分布关系,然后提出了一种双阈值最优化策略保证特征点的区分性和稳定性。
1 双自适应稳定SIFT算法 1.1 SIFT算法基本原理
SIFT算法主要分为3个部分[3]:① 尺度空间特征点检测和定位;② 生成特征点描述符;③ 特征匹配。高斯核是建立尺度空间的唯一线性核,通过方差不断增大的高斯函数与图像卷积,可建立图像的尺度空间表达。其表达式为:
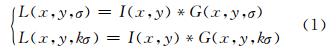
式中,L(x,y,σ)为高斯尺度空间,如图 1所示;I(x,y)为原图像;G(x,y,σ)为标准差为σ的高斯函数;k为尺度变化量;*代表卷积运算。
|
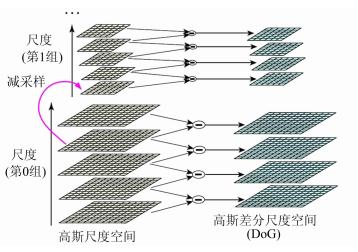
| 图 1 SIFT尺度空间 Fig. 1 SIFT Scale Space |
SIFT算法采用高斯拉普拉斯算子(Laplace of Gaussian,LoG)检测图像中的极值点,并用高斯差分尺度空间(difference of Gaussian,DoG)近似,其表达式为:
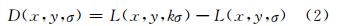
式中,D(x,y,σ)为高斯差分尺度空间。
图像的尺度空间分为若干组,相邻两组之间的图像尺寸相差2倍。每组分为若干层,高斯函数标准差逐层递增,不同组的相同层采用相同的高斯核进行逐级模糊。
对检测到的特征点,统计邻域梯度方向的直方图,确定主方向;旋转邻域到水平方向,统计分块梯度方向的直方图,得到128维描述子。然后利用描述子间的欧氏距离建立匹配对,通过RANSAC(random sample consensus)算法筛选出正确的匹配点。
1.2 尺度空间分布
由于SAR的成像特性,图像上存在大量的乘性噪声,尤其是高斯尺度空间的第一组数据受噪声干扰严重,影响正确匹配点的确定。去除高斯尺度空间的第一组数据,由第二组数据开始建立大尺度高斯尺度空间,可以去除不稳定细小纹理对特征提取的影响[5]。下文中尺度空间的分析都是针对大尺度高斯尺度空间进行的。
尺度空间内合理分布特征点的问题也就是合理分布尺度空间中不同组 (o)和层(l)特征数目(No,l)的问题。假设所有组、层中提取的特征总数是N,则有:
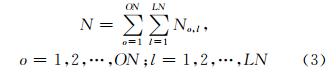
其中,ON是尺度空间组数;LN是每组中包含的层数。
在尺度空间中,每组的第一层是由上一组第一层图像降采样一倍得到的(图 1),所包含的像素数为上一组同层图像所包含像素点数的1/4,在同等模糊程度下,图像提取的特征数目与像素数目成正比,所以不同组之间的待提取特征数目符合式(4):
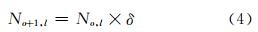
式中,No,l表示第o组l层提取的特征点数;No+1,l表示第o+1组l层待提取的特征点数;δ是相邻组内同层图像可提取特征数目的比例系数,δ=1/4,针对SAR数据高尺度空间乘性噪声干涉较弱的特点,适当增加高尺度空间内提取的特征点数,可以减少噪声影响,保证提取特征的稳定性,因此将比例系数δ调整为1/3。
尺度空间不同层的图像之间是一种逐级模糊、平滑过渡的关系(如式(1)),所以各层中可提取的极值点数目成等比数列关系[2],而下一组的第一层图像是由上一组第一层图像经过LN次高斯模糊得到的,所以有关系式:
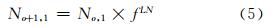
其中,f表示逐级模糊的图像可提取特征点数之间的比例系数。
假设第1组1层图像预分配的特征点数是 N1,1,则由等比数列性质,第o组l层图像分配的特征点数如下:
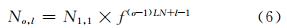
由等比数列求和公式,可知第o组l层中的特征点数目No,l为:
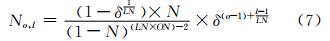
其中,N是尺度空间中待提取的特征点总数。
1.3 图像空间分布
SAR数据噪声干扰、局部畸变严重,提取同名点的难度较大,因此在控制SIFT特征均匀分布的同时,要保证特征点的稳定性和区分性。本文选取图像信息熵作为自适应控制特征点分布的 局部纹理,以保证特征点的区分性,通过双阈值最优化筛选可以在保证提取特征点稳定性的同时,尽量多地提取符合要求的特征点。文献[6]通过理论分析和实验验证,表明特征点匹配的可能性与特征区域的信息熵之间有密切的关系,尽管匹配结果受到特征实际情况的影响,但是正确匹配的概率会随着特征点附近区域信息量的增加而增加。
在信 息论中,信息熵被定义为随机变量的数学期望,它表现了集合中随机事件出现的平均不确定性。图像的信息熵E定义为:
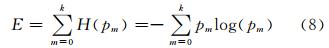
其中,k是图像所包含的灰度级;pm表示整幅图像中灰度为m的像素出现的概率。
在确定尺度(o,l)的图像空间中,将待提取图像数据分割成N×M块区域图像,每块内提取的特征点数的计算式如下:
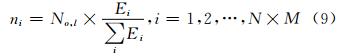
式中,ni是图像空间中第i个图像块中分配的特征点数;No,l是由式(7)得到的尺度空间中第o组l层中分配的特征点数;Ei是图像空间中第i个图像块的图像信息熵。
1.4 双阈值最优化筛选策略
极值点的稳定性取决于极值点处对比度的大小[7],为了保证选取的特征点的稳定性更强,对检测出的极值点使用最优化筛选的方法,按照极值点处对比度从高到低的顺序排序,选取其中对比度最大的ni个极值点作为SIFT特征点;为了保证算 |法的鲁棒性,采用双阈值筛选的方法,设置低阈值为Tcmin,只有对比度大于Tcmin的特征点才作为待选的SIFT特征点,同时设置高阈值Tcmax,计算第 ni+1个特征点的对比度D(
2 SAR数据匹配试验
为了验证算法的有效性,设计了两组试验,分别使用SIFT算法[3]、UR-SIFT算法[2]、大尺度UR-SIFT算法以及本文提出的DAS-SIFT算法,对机载SAR数据、星载SAR数据进行同名点提取试验,从算法效率、匹配正确率、提取正确同名点数、分布质量(distribution quality,DQ)4个方面进行比较分析。
2.1 空间分布质量评价标准
配准图像的鲁棒性和准确度取决于提取同名点的分布质量[8, 9]。文献[8]中对遥感数据尝试用不同数目的同名点配准图像,发现同名点的数目不能决定配准精度,图像配准精度与同名点的分布质量相关。
空间分布质量(DQ)是根据特征点的空间分布和信息熵[9]计算的,计算公式如下:
式中,M和N分别为图像的行数和列数; xi,yi 是第i个特征点的坐标;n是特征点的总数; (x,y)采用式(11)计算:
式中,wi是第i个特征点的权重,以特征点的局部信息熵(式(8))作为权重。
2.2 机载SAR匹配试验
本组试验选取的是2010年四川绵阳两幅机载SAR图像X波段斜距数据,尺寸都是3 000×3 000,分辨率为0.5 m,有明显的亮度差异。图 2分别是SIFT算法、UR-SIFT算法以及DAS-SIFT算法进行匹配试验提取出的同名点情况。可以看出,标准SIFT算法提取出的同名点集中在特征明显的区域;UR-SIFT算法提取的同名点对比SIFT算法提取的同名点对分布更均匀,但是数量有所减少,尤其在噪声干扰较大的区域提取的同名点不足;本文算法无论从同名点数量还是分布均匀度方面,都有明显提升。
图 3是特征点的尺度空间分布情况。标准SIFT算法和UR-SIFT算法的尺度空间包含4组三层数据,而DAS-SIFT算法是在大尺度空间内 进行的,仅包含3组三层数据。SIFT算法包含所有符合极值点条件的特征点,所提取的特征较多;UR-SIFT算法和DAS-SIFT算法的特征总数是一样的,但是不同组和层之间的分布情况不同。
表 1从运行时间、特征数目、匹配点对数、空间分布质量四个方面对比了三种算法。从表 1中可以看出,由于本文算法是在大尺度空间检测特征点,而且使用计算效率较高的图像信息熵作为局部纹理度量标准,运算效率高,耗时最短;采用双阈值最优化筛选策略选取特征点,在保留高区分性特征点的同时,又去除了对比度低的不稳定点,不仅特征点匹配的正确率高,而且可以提取更多的同名点。
为了着重分析信息熵自适应分布和双阈值最优化筛选策略的有效性,这里进行了大尺度UR-SIFT算法对比试验。试验数据是两幅Cosmo卫星获取的四川成都地区包含山区和城市场景的数据,图像尺寸分别为4 540×3 140和4 796×3 658,获取时间分别是2011年7月和2011年5月。相对于山区,城市地区特征明显,容易提取更多的特征点。
图 4是不同算法进行匹配试验提取的同名点情况。从图 4中可以明显看出,标准SIFT算法和UR-SIFT算法提取出的同名点主要集中在特征明显的城市区域,山区场景特征点提取的数量较少,尤其是如图 4(a)、4(b)方框所示区域;大尺度UR-SIFT算法在特征不明显的山区提取的同名点数有所增加,相应的特征分布质量有所提升,如图 4(c)中的方框区域;而本文提出的DAS-SIFT算法不仅在特征明显的城市区域能提取出一定数量、分布均匀的同名点,而且在特征不明显且存在局部畸变的山区,也能提取出数量和分布合理的同名点,如图 4(d)中的方框区域。表 2定量描述了四种算法同名点的提取情况。
针对SAR图像数据匹配过程,提出了一种自适应控制同名点均匀分布的算法。算法可应用于机载和星载SAR数据,即使是对于场景复杂的图像数据,也可以提取出一定数量且分布合理的稳定特征点,而且具有一定的抗噪声干扰和局部畸变影响的能力。与原始的SIFT算法相比,本文算法可能会减少一些匹配点 对的数目,但是在计算效率、分布质量等方面得到了有效的改善。
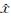 )|ni+1,如果|D(
)|ni+1,如果|D(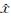 )|ni+1>Tcmax,则保存第ni+1个特征点,继续计算,直到|D(
)|ni+1>Tcmax,则保存第ni+1个特征点,继续计算,直到|D(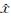 )|ni+l
)|ni+l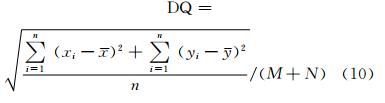


图 2 不同算法提取同名点试验
Fig. 2 Matches Extracted Experiments
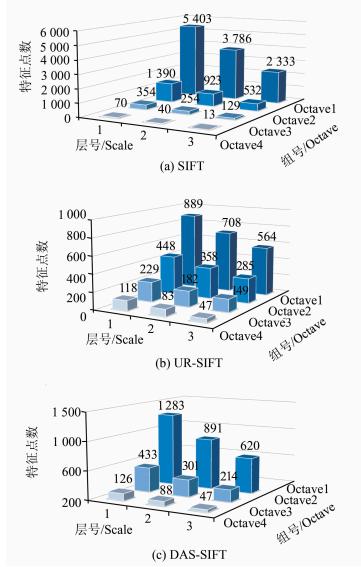
图 3 不同算法尺度空间内特征分布情况
Fig. 3 Features Distributions in Scale Space
方法 SIFT UR-SIFT DAS-SIFT
运行时间/s
62.75
23.30
15.60
待匹配影像对的左图特征数/个
15 527
4 060
4 011
待匹配影像对的右图特征数/个
24 041
4 062
4 003
匹配点/特征点
715/839
547/575
826/845
DQ
0.191
0.197
0.205

图 4 不同算法提取同名点试验
Fig. 4 Matches Extracted Experiments
方法 SIFT UR-SIFT 大尺度UR-SIFT DAS-SIFT
运行时间/s
67.92
33.41
19.86
18.70
待匹配影像对的左图特征数/个
11 456
4 082
3 731
4 032
待匹配影像对的右图特征数/个
33 382
4 092
3 869
4 053
匹配点/特征点
33/142
55/100
81/141
109/142
DQ
0.171
0.189
0.206
0.212
| [1] | Sedaghat A, Mokhtarzade M. Uniform Robust Scale-Invariant Feature Matching for Optical Remote Sensing Images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(11):4 516-4 527 |
| [2] | Song R, Szymanski J. Well-distributed SIFT Features[J]. Electronics Letters, 2009, 45(6):308-310 |
| [3] | Lowe D G. Distinctive Image Features from Scale-invariant Keypoints[J]. International Journal of Computer Vision, 2004, 60(2):91-110 |
| [4] | Lingua A, Marenchino D, Nex F. Performance Analysis of the SIFT Operator for Automatic Feature Extraction and Matching in Photogrammetric Applications[J]. Sensors, 2009, 9(5):3 745-3 766 |
| [5] | Wang Shanhu, You Hongjian, Fu Kun.BFSIFT:A Novel Method to Find Feature Matches for SAR Image Registration[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(4):649-653 |
| [6] | Zhu Qing, Wu Bo, Wan Neng.An Interest Piont Detect Method to Stereo Images with Good Repeatability and Information Content[J]. Acta Electronica Sinica, 2006, 34(2):205-209(朱庆, 吴波, 万能.具有良好重复率与信息量的立体影像点特征提取方法[J].电子学报, 2006, 34(2):205-209) |
| [7] | You Zhai, Luan Zeng.A SIFT Matching Algorithm Based on Adaptive Contrast Threshold[C]. Consumer Electronics, Communications and Networks (CECNet), Xianning, China, 2011 |
| [8] | Zhu Qing, Wu Bo, Wan Neng. Seed Point Selection Method for Triangle Constrained Image Matching Propagation[J]. IEEE Geoscience and Remote Sensing Letters, 2006, 3(2):207-211 |
| [9] | Zhang Ye, Guo Yan, Gu Yanfeng. Robust Feature Matching and Selection Method for Multi Sensor Image Registration[C]. International Geoscience and Remote Sensing Symposium (IGARSS), Cape Town, South Africa, 2009 |
 2015, Vol. 40
2015, Vol. 40


