文章信息
- 孙晗伟, 曾涛, 杨健, 李文梅
- SUN Hanwei, ZENG Tao, YANG Jian, LI Wenmei
- SAR残余相位误差对森林高度反演影响的全链路模拟与分析
- Simulation and Analysis of SAR Residual Phase Error on Forest Height Inversion
- 武汉大学学报·信息科学版, 2015, 40(2): 153-158
- Geomatics and Information Science of Wuhan University, 2015, 40(2): 153-158
- http://dx.doi.org/10.13203/j.whugis20130052
-
文章历史
- 收稿日期:2013-04-16
2. 北京理工大学信息与电子学院, 北京 100081;
3. 中国林业科学研究院资源信息研究所, 北京 100091
2. School of Information and Electronics, Beijing Institute of Technology, Beijing 100081, China;
3. Institute of Forest Resources Information Technique, Chinese Academy of Forestry, Beijing 100091, China
利用合成孔径雷达(synthetic aperture radar,SAR)遥感手段进行森林调查和制图已成为一种有效的途径。森林资源的定量反演建立在掌握地理学和生物学规律的基础上,是根据SAR观测信息和森林微波散射模型求解或推算描述森林生物学应用参数的过程。反演的困难在于应用参数往往不是反映遥感数据特征的主导因子,只与遥感信息弱相关[1]。因此,遥感过程每个环节引入的误差、不稳定等因素都会对定量反演精度造成影响,导致反演结果具有不确定性[2]。SAR 系统不确定性因素对传统SAR应用(以图像辐射性能为主要对象)的影响已得到了大量的研究和分析[3]。但是,林业遥感应用不仅对图像的辐射精度有要求,更对图像的相位精度(特别是干涉精度、极化精度)有较高要求,而目前从森林参数反演精度出发对各类不确定性因素的定量分析仍较为欠缺。
目前,分析SAR系统的不确定性因素对反演精度影响的方法主要有基于实测数据和基于模拟数据两种。实测数据中存在各种不确定性因素,从影像出发难以解耦,因此分析结果可能耦合各类不确定性因素的影响,而且数据来源有限,难以获取误差量的确切值。而通过数据模拟可解决这一问题。一方面,在模拟过程中,便于将各种不确定性因素解耦,可以分别进行模拟,也可以联合模拟,有利于对不确定性因素单独或联合分析;另一方面,采用模拟的手段可以获取大量的可变参数的遥感数据,可弥补实测数据的不足,有利于建立不确定性因素与反演精度之间较完整的定量化关系。其中,文献[4, 5]采用PolSARprosim[6]模拟的方式分别分析了通道不平衡对极化干涉性能和森林高度估计的影响,以及极化串扰和通道不平衡对极化相干最优的影响。
但是,基于模拟数据的分析结果其可靠性建立在模拟模型的准确度之上。PolSARprosim是典型的SAR林业遥感模拟软件,采用SAR图像直接模拟的方式,且点扩展函数为二维高斯函数,获取的模拟数据较为理想。而SAR系统的各项不确定性因素属于遥感数据的获取阶段,其影响首先作用于SAR回波信号,在信号处理过程中,这些因素的影响可能被纠正或放大,并传递至SAR图像中。在理想的SAR图像中加入不确定性因素的影响,与不确定性因素的作用阶段不符,分析结果很可能受模拟数据精度的影响。
本文首先建立了极化SAR三维森林场景遥感数据的全链路模拟模型,采用了基于方位时域的SAR回波信号模拟方法,考虑了各类不确定性因素对回波信号的作用,在作用源头对不确定性因素进行了描述,与实际遥感系统的工作过程一致;然后基于E-SAR样地数据及实测数据对模拟模型进行了验证;最后以全链路模拟模型为基础,以森林高度反演这一典型林业应用为对象,定量分析了运动补偿残余相位误差这一典型的SAR系统不确定性因素对反演精度的影响程度。
1 全链路模拟模型
本文讨论的极化SAR三维森林场景遥感数据的全链路模拟包括三个步骤。首先,综合考虑地形、林木分布、林木大小以及单木生长结构,建立林分的几何模型;其次,根据三维森林冠层内各个散射介电粒子的大小、指向角、雷达的频率以及电磁波入射和出射方向,并采用合适的散射模型计算每个散射介电粒子的多极化后向散射系数;然后建立极化SAR信号模型,充分考虑SAR系统的各类不确定性因素,包括运动特性、天线特性、接收机特性、极化特性等,模拟生成极化SAR回波数据,并通过成像聚焦获取三维森林场景极化SAR图像。
1.1 树木几何模型
本文采用整体几何结构模型构造单木三维结构[7]。该方法提供从树根到树叶的任意路径,通过树木分叉的数目、分叉的角度、树枝长度、半径变化和各种扰动来构造模型,从整体结构出发用若干参数对树木造型进行控制。树木关键参数(胸径、冠层厚度、枝叶大小等)的计算均通过生物学公式或经验值获取,在一定程度上保持了所构造树木的生物特性,同时采用递归迭代的计算方法保证了计算机处理的高效性。树木建模效果如图 1所示。树木生长位置在林分尺度内采用蒙特卡罗随机获得,相邻树木之间保持合理的间距。
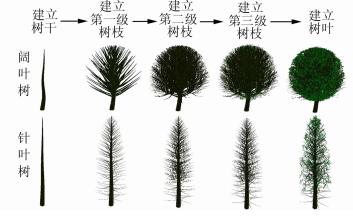
|
| 图 1 树木建模过程及效果示意图 Fig. 1 Tree Modeling Process and Effect |
与可见光、近红外相比,微波波段的穿透性较强,与森林发生电磁作用时,能够穿透树冠与枝干、地表面发生作用,形成多种散射机理[6, 8],如图 2所示。

|
| 图 2 森林微波散射机理示意图 Fig. 2 Microwave Scattering Mechanism of Forest |
图 2中,1表示地表的面散射,用Sg表示;2表示树体(干、枝、叶)的直接散射,用St表示;3表示地表散射波作用于树体后返回雷达的二次散射(double bounce),用Sgt表示;4表示树体散射波作用于地表后返回雷达的二次散射,用Stg表示;5表示地表散射波被树体散射后又与地表发生作用后返回雷达的多次散射,用Sgtg表示。
不同的散射介电粒子根据几何尺寸的大小选择不同的单粒子散射模型[8]。对于粗大枝干,采用有限长介电圆柱体(finite dielectric cylinder)模型计算单体散射[8];对于细小枝干和针叶片,采用GRG近似(generalized rayleigh-Gans approximation)的针状体模型计算单体散射[8];对于阔叶片,采用GRG近似的圆盘体模型计算单体散射[8]。 1.3 极化SAR信号模型
由SAR工作原理可知,一个脉冲的回波信号可表示为考虑一定微波散射特性、具有幅度衰减和时间延迟的发射信号[9]:
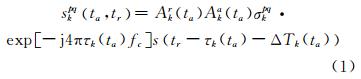
式中,pq分别为h极化或v极化;skpq(ta,tr)为第k个散射粒子的回波信号;ta表示方位向慢时间;tr表示距离向快时间;Akr(ta)为考虑了包括距离衰减、天线方向加权、系统损耗等因素的雷达方程因子;σkpq为散射粒子的极化散射系数;τk(ta)为散射粒子距离延迟;fc为发射信号载频;s(t)为发射信号形式;Aka(ta)表示大气衰减因子;ΔTk(ta)为大气附加延迟。
根据森林微波散射模型,森林场景可看成是大量散射介电粒子组成的,整个森林场景的回波信号就是各个散射介电粒子回波信号的相干叠加:
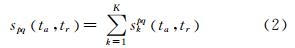
其中,K为森林场景的散射粒子个数。
结合极化串扰模型、极化通道不平衡模型、极化偏转模型、接收机热噪声模型,最终全极化 SAR三维森林场景遥感回波信号可以写成如下的矩阵形式:
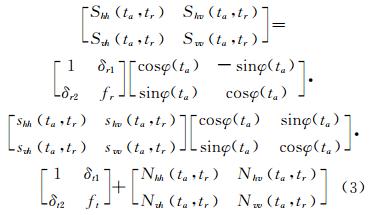
式中,δt1、δt2表示发射过程极化串扰;δr1、δr2表示接收过程极化串扰;ft、fr分别表示发射和接收通道的极化不平衡;φ ta 为不同方位脉冲时刻的极化偏转角;Npq为不同极化通道的热噪声。式(3)可以较完整地描述极化 SAR回波信号,实现了SAR遥感系统的全链路模拟。
2 模型验证
本文采用DLR(德国宇航中心)E-SAR系统获取的森林样地观测数据作为比较对象,根据E-SAR系统参数和实测样地参数,采用本文的模拟模型生成极化SAR森林干涉图像对,利用相位-幅度联合反演法[10]分别基于模拟数据和实测数据反演树木高度,对比反演结果。
2.1 E-SAR实测数据及参数
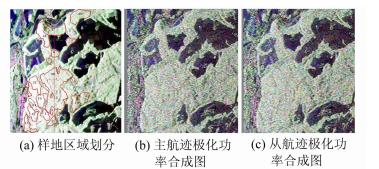
实测数据为E-SAR系统于2003年10月11日通过重轨飞行获取的极化干涉SAR影像数据(如图 3所示),试验区位于德国南部城市Traunstein附近,地表实测数据覆盖123 hm2的20个样地,树种以针叶松(云杉、冷杉)为主。E-SAR系统参数如表 1所示。
|
| 图 3 样地区域划分及E-SAR样地极化干涉SAR影像对 Fig. 3 E-SAR Pauli Image and Plots Dipartition |
| 参数 | 取值 | 参数 | 取值 |
| 飞行高度 | 3 024 m | 入射角 | 50° |
| 飞行速度 | 98.9 m/s | 脉冲重复频率 | 400 Hz |
| 信号带宽 | 100 MHz | 采样率 | 110 MHz |
| 分辨率 | 1.5 m×3 m | 波段 | L(1.3 GHz) |
| 水平基线 | 4.35 m | 垂直基线 | 0.067 m |
| 极化串扰度 | -30 dB | 极化通道不一致性 | 幅度±1 dB,相位±10° |
样地平均树高30 m。模拟参数采用E-SAR系统参数,样地面积为4 hm2,密度为162株/hm2。根据样地参数,按照§1.1的模型获取林分分布和单株树木几何结构,根据E-SAR系统参数按照§1.2和§1.3的模型分别计算样地林分的微波散射和主从阵元极化SAR回波信号,并采用CS(chirp scaling)成像算法进行距离向和方位向聚焦处理,最终得到主从阵元模拟图像。
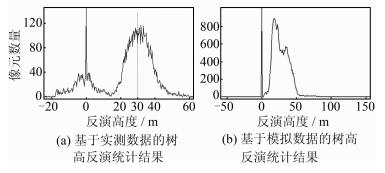
分别基于实测影像和模拟影像提取森林高度,得到如图 4所示的统计结果。可以看到,实测数据的高度反演结果主要分布在30 m附近,平均树高为27.3 m,0附近出现了一些分布,可能是由于存在杂草、灌木等低矮植被引起的,使平均高度统计结果有所降低,而利用模拟数据反演的平均高度为30.7 m,与样地测量结果一致。另外,从高度统计结果可以看到,模拟数据和实测数据的反演结果均存在负值和超过50 m的反演结果,这些值超出了合理的范围,可能为传感器不确定性因素引起的。这说明模拟数据和实测数据的特征具有较强的一致性,全链路模拟模型的有效性得到了验证。
|
| 图 4 基于实测数据和模拟数据的树高反演统计结果 Fig. 4 Forest Height Inversion Results |
利用全链路模拟模型,针对SAR运动补偿后的残余相位误差这一典型的SAR系统不确定性因素,定量分析其对森林高度反演精度的影响程度。模拟基于E-SAR的系统参数,样地为4 hm2的阔叶林,其中120 m×120 m范围内为林地区域,其他区域为草地;林分密度为300株/hm2,共376株,平均树高10 m。林木分布及理想情况下的模拟和反演结果如图 5所示。

|
| 图 5 模拟样地及理想情况下模拟和反演的结果 Fig. 5 Simulation and Inversion Results Under Ideal Condition |
将SAR平台的航迹变化分解为理想航迹和误差航迹,实际的航迹为二者的叠加合成,因此造成的雷达到目标的斜距误差可以写成理想斜距和误差斜距相叠加的形式:
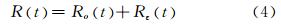
式中,Ro t 表示理想航迹产生的斜距变化;Rε t 表示误差航迹产生的斜距变化。假设运动补偿后恒定的位置误差、恒定的速度误差和恒定的加速度误差均被补偿,仅残余正弦形式的误差,则雷达到目标的残余斜距误差可以表示为:
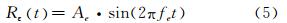
其中,Ae、fe分别为残余斜距误差的幅度和频率。多普勒相位误差为:
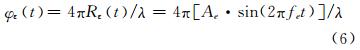
设置残余相位误差分别为π/2、π/4、π/8和π/16,残余误差的正弦调制频率分别为0.5 Hz(低频)、3 Hz(中频)和10 Hz(高频)。采用本文的极化SAR三维森林场景全链路模型获得模拟样地在不同误差参数下的干涉SAR图像对,并进行森林高度反演,模拟影像及反演结果如图 6所示。可以看到,与理想情况下的反演结果相比(图 5),当高频抖动时,即使在相位误差为π/16的情况下,森林高度反演图中仍能体现出残余相位误差的影响;当低频抖动时,这一影响在相位误差为π/8时基本消失。
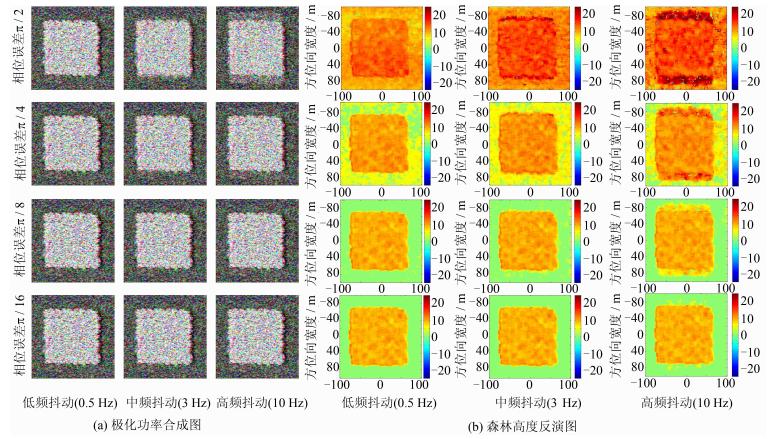
|
| 图 6 存在残余相位误差时全链路模拟和森林高度反演结果 Fig. 6 Simulation and Inversion Results with Residual Phase Errors |
针对残余相位误差对森林高度反演精度的影响程度进行RMSE测量。先给出森林高度反演RMSE的计算方法,如式(7)所示:
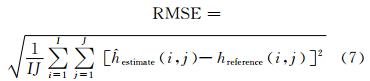
式中, estimate为基于含有不确定性因素的模拟数据反演得到的高度估计;hreference为基于理想的模拟数据反演得到的高度估计;I、J分别表示SAR影像中选定的林分区域二维像元数。
estimate为基于含有不确定性因素的模拟数据反演得到的高度估计;hreference为基于理想的模拟数据反演得到的高度估计;I、J分别表示SAR影像中选定的林分区域二维像元数。
将§3.2得到的森林高度反演的RMSE测量结果与相位误差的关系曲线如图 7所示。可以得出,若使森林高度反演的RMSE测量结果优于1 m,则在低频抖动(0.5 Hz)情况下,应控制残余相位误差在0.45 rad以下;在中频抖动(3 Hz)情况下,应控制残余相位误差在0.36 rad以下;在高频抖动(10 Hz)情况下,应控制残余相位误差在0.23 rad以下。本文是在典型抖动的频率下给出了上述分析结果,当抖动频率进一步增大时,对残余相位误差的控制精度应进一步提高。

|
| 图 7 运动补偿残余相位误差-RMSE关系曲线 Fig. 7 Curves of Residual Phase Errors and RMSE |
本文建立了极化SAR三维森林场景遥感数据的全链路模拟模型,考虑了各类不确定性因素对回波信号的作用,并基于E-SAR实测样地参数及数据验证了模型的有效性。为了满足反演精度的需求,需将残余相位误差控制在较小范围内(本文参数条件下小于0.23 rad)。与传统SAR聚焦的控制需求(π/4)相比,森林高度反演应用对雷达系统和信号处理的精度提出了更高的要求。
需要说明的是,本文的模拟和分析结果是在指定的参数和处理算法下以森林高度反演这一典型应用得到的。不同参数、算法等条件下,不确定性因素的敏感性并不相同,因此需具体问题具体分析。本文的主要工作和成果为SAR林业遥感不确定性问题的研究提供了一个有效途径,可以为SAR林业遥感系统设计、指标控制提供参考,并可辅助实验系统进行性能评价。
| [1] | Li Xiaowen.Retrospect Prospect and Innovation in Quantitative Remote Sensing[J]. Journal of Henan University, 2005, 35(4):49-56(李小文. 定量遥感的发展与创新[J].河南大学学报, 2005, 35(4):49-56) |
| [2] | Ge Yong.Aircraft Synthetic Aperture Radar Uncertainty Analysis—Theory, System and Application[D].Beijing:Institute of Geographic Sciences and Natural Resources Research, Chinese Academy of Sciences, 2001(葛咏.机载合成孔径雷达(SAR)不确定性分析——理论、系统及应用[D]. 北京:中国科学院地理科学与资源研究所, 2011) |
| [3] | De Macedo K A C, Scheiber R, Moreira A. An Autofocus Approach for Residual Motion Errors with Application to Airborne Repeat-Pass SAR Interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(10):3 151-3 162 |
| [4] | Zhang Lintao, Hong Jun, Ming Feng. Study on the Impact of Polarimetric Error on Optimal Coherence Phase of PolInSAR[J]. Journal of Electronics & Information Technology, 2011, 33(2):412-417(张林涛, 洪峻, 明峰. PolInSAR极化误差对最优相干相位的影响研究[J]. 电子与信息学报, 2011, 33(2):412-417) |
| [5] | Chen Jiehong, Zhang Hong, Wang Chao. Channel Imbalance of Polarization Interference Performance and Effect of Forest Height Estimation[C]. Advanced SAR for Earth Observation, Beijing, China, 2011(陈皆红, 张红, 王超. 通道不平衡对极化干涉性能和森林高度估计影响的研究[C].成像雷达对地观测高级学术研讨会, 北京, 2011) |
| [6] | Williams M L. The Theory for a Forward SAR Model:Implementation, Applications and Challenges[C]. EUSAR, Dresden, Germany, 2006 |
| [7] | Weber J, Penn J. Creation and Rendering of Realistic Trees[C]. International Conference on Computer Graphics and Interactive Techniques, New York, USA, 1995 |
| [8] | Sun Guoqing, Ranson K J. A Three-Dimensional Radar Backscatter Model of Forest Canopies[J]. IEEE Transactions on Geoscience and Remote Sensing, 1995, 33(2):372-382 |
| [9] | Zhang Shunsheng.Study on Natural Scene Simulation of SAR[D]. Beijing:Beijing Institute of Technology, 2007(张顺生. 合成孔径雷达自然场景回波仿真技术研究[D]. 北京:北京理工大学, 2007) |
| [10] | Cloude S R. Polarization Coherence Tomography[J]. Radio Science, 2006, 41(4):RS4017.1-RS4017.27 |
 2015, Vol. 40
2015, Vol. 40


