文章信息
- 郑顺义, 王晓南, 马电
- ZHENG Shunyi, WANG Xiaonan, MA Dian
- 一种便捷式小型物体三维重建方法
- A Convenient 3D Reconstruction Method of Small Objects
- 武汉大学学报·信息科学版, 2015, 40(2): 147-152
- Geomatics and Information Science of Wuhan University, 2015, 40(2): 147-152
- http://dx.doi.org/10.13203/j.whugis20130515
-
文章历史
- 收稿日期:2013-09-22
物体的数字化三维重建是 增强现实、三维测量、逆向工程等技术中的重要组成部分,它把现实世界中的感兴趣目标转换为数字三维模型,用于虚拟展示、形状分析、3D打印等目的。个人电脑、数码相机和智能手机的普及,CPU和GPU计算性能的提升,网络社交的兴起等要素结合起来,使得个人手拍影像,并能建立三维模型,进行自娱自乐并发布的时代到来了,这样的预测或期待越来越接近现实,越来越被更多的人所关注[1]。
多视匹配[2]是从二维影像到三维模型的基本方法,在计算机视觉和摄影测量领域已有大量成熟可靠的匹配算法[3, 4, 5]。然而此类方法对物体的纹理特性和反射折射特性十分敏感,它只适用于纹理丰富且具有朗伯特均匀漫反射表面的物体,这大大限制了此类方法的适用范围。
另一种由二维影像建立三维模型的方法是基于轮廓线的方法,Baumgart[6]最早提出了此类方法的思想;Laurentini[7]首先实现了此类方法并提出了视外壳(visual hull)的概念;Matusik[8]、Sinha[9]和Yemez[10]分别使用不同的影像采集系统实现了此类方法,但它们都需要经过繁琐的标定和精密的控制,带有很强的实验室性质;Lazebnik[11]和Furukawa[12]在Sinha的研究基础上总结出支撑轮廓线的脊线(rim)的概念,但精确定位脊线需要用到影像匹配,这在适用性意义上是一种退化;曹煜[13]利用两块平面反射镜来实现单张影像获取五个视角的虚像,是一种便捷的方法,但五个视角不足以实现较高精度的三维重建,文中也没有给出拍摄多张影像如何进行姿态恢复的方法;Liang等[14]使用视角相近的影像来确定轮廓交叉点,但这种方法不适用于影像数量少、视角分散的情况;Díaz-Más[15]、Haro[16]等研究了如何在影像的轮廓线存在误差(或错误)的情况下保证重建的正确性,但他们没有考虑如何直接在影像上降低轮廓线的误差。由于用体素来表示三维模型会在精度上依赖于体素的分辨率,因此Xia等[17]提出了一种内插轮廓线的方法,但其使用的轮廓线图像仍然是二值图像,轮廓边缘的锯齿现象并没有得到改善。基于视频流和轮廓线的三维重建也用于模式识别[9, 18],但这一领域对模型精度的要求较低,重建的模型不适用于虚拟展示等目的。
手机是日常生活最常用的工具,本文研究了如何从手拍影像建立三维模型,重点解决的关键问题有:①通过对背景的设计,稳定可靠地获取每张影像的内外方位元素;②在复杂背景下,方便快捷地提取物体的轮廓线;③以较低的计算成本快速生成三维模型,最终实现一种方便快捷、稳定可靠的三维重建方法,为个人手拍、建立三维模型并网络发布提供一种新的途径。
1 便捷式小型物体三维重建方法
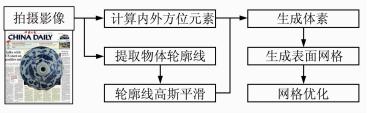
本文使用手机摄像头(或其他便携式设备)按自由方位采集影像,无需精密的人工标定物或机械转台,但要求在物体下面放置一张纹理丰富且符合朗伯特反射的材料(如报纸),物体和背景材料保持相对静止。本文方法的流程图见图 1。
|
| 图 1 本文方法流程图 Fig. 1 Flow Chart of Our Method |
以随意性选择的环境为背景,往往由于纹理匮乏、镜面反射等原因无法获取稳定可靠的同名点,在特意选择纹理丰富的背景下,用SIFT特征匹配可以获得大量稳定的同名点,影像的内外方位元素可以使用从运动到结构(structure from motion,SFM)的方法获取[19, 20, 21]。匹配同名点之后,使用具有鲁棒性的随机抽样一致性算法(random sample consensus,RANSAC)确定影像两两之间的关系(核线关系、单应关系或者不重叠),存在核线关系的构成立体像对。然后根据立体像对之间的公共点将所有立体像对连接构成自由网。最后利用光束法平差(bundle adjustment)做整体优化[22, 23]。本文所使用的相机模型如下(由于手机的自动对焦功能,每张影像具有独立的内方位元素):
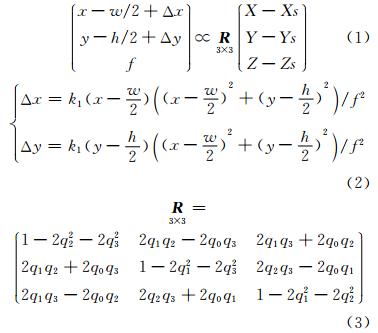
式(1)~式(3)中,∝代表齐次等于(正比于);(x,y)代表影像上以左下角为原点、以像素为单位的像点坐标; w代表影像宽;h代表影像高;影像中心(w/2,h/2)为像主点;f代表以像素为单位的主距;(Δx,Δy)代表像点畸变;k1代表归一化的径向畸变参数;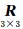 代表旋转矩阵; X,Y,Z 代表对应的物方坐标;(Xs,Ys,Zs)代表影像的摄影中心在物方坐标系中的坐标;(q0,q1,q2,q3)代表单位四元数,用来表示旋转。在以上参数中,像主点固定,需要解算的内方位元素有f和k1,外方位元素有(Xs,Ys,Zs)和(q0,q1,q2,q3)。
代表旋转矩阵; X,Y,Z 代表对应的物方坐标;(Xs,Ys,Zs)代表影像的摄影中心在物方坐标系中的坐标;(q0,q1,q2,q3)代表单位四元数,用来表示旋转。在以上参数中,像主点固定,需要解算的内方位元素有f和k1,外方位元素有(Xs,Ys,Zs)和(q0,q1,q2,q3)。
以上方法可以稳定可靠地获取影像参数,避免了采用专门设计的标定板或其他实验装置,大大增加了该三维重建方法的灵活性。
1.2 提取轮廓线及高斯平滑
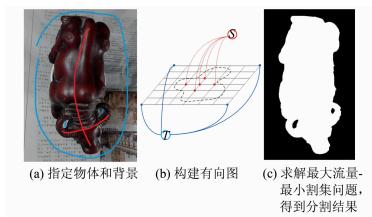
全自动提取轮廓线的方法一般要求背景色调单一,这与§1.1要求使用纹理丰富的材料作为背景是矛盾的,而全手工勾勒轮廓线的工作量大,十分耗时。考虑到物体的轮廓线是两边色调差异较大的分界线,故使用图割法[24, 25]来半自动分离影像中的物体和背景,Schmidt[26]为平面图割提供了一种快速实现。如图 2所示,首先人工在影像指定物体和背景,然后构建有向图,最后求解网络最大流量-最小割集问题,得到物体和背景的分割结果,如果分割有不合理的地方,则增加人工指定物体或者背景(如图 2(a)中的牛角处增加指定背景),直到认为分割结果合理为止。
|
| 图 2 基于图割法的背景分割 Fig. 2 Background Segmentation via Graph Cuts |
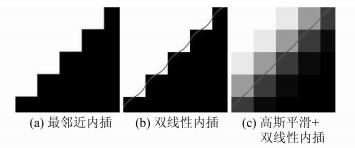
在完成背景分割之后,得到一幅二值图像,灰度值255代表物体,灰度值0代表背景(图 2(c)),而灰度值等于128的等值线称为轮廓线。如果使用最邻近内插(图 3(a)),则轮廓线含有明显的“锯齿”效应,使用双线性内插(图 3(b)),则轮廓线呈“波浪”线状,起伏有0.2像素。为了削弱这种现象,本文对二值图像先进行一次高斯平滑(图 3(c)),然后使用双线性内插,更加符合实际形状。可见, 自动、快速、稳定的轮廓提取方法大大缓解了影像数增加所带来的轮廓线提取的工作量。
|
| 图 3 灰度值为128的等值线(轮廓线) Fig. 3 Contour Line with Grey Value Equals 128 (silhouette) |
给定三维空间内的一个立方体,将其均匀地分割为N×N×N份(本文中N=512),其中每一个最小单元的立方体称为一个体素(voxel),假设物体位于立方体内部,则所有与物体表面“相交”的体素的集合称为该物体的体素模型。Martin[27]最早使用体积分割(volume segment)的方法来重建三维形状,然后发展为基于体素和八叉树的方法[28],以及基于体素和交叉点的方法[29],这两种方 法的时间复杂度均为O(M×N2),其中M是影像的数量。但两种方法都存在冗余计算,其中八叉树方法的冗余计算量在一倍以上(考虑一个有效的ON节点,其父节点的8个子节点中平均有4个为ON节点,其余为冗余计算)。本文通过引入两种技术来降低生成体素模型的计算成本。
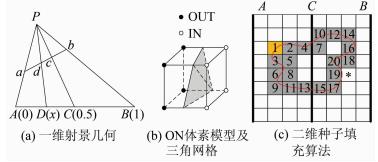
1) 基于交比(cross ratio)不变量的像点坐标快速计算。交比是射影几何中的不变量,在消除影像的畸变之后,空间直线与其在影像上的投影直线存在射影变换关系,如图 4(a)中共线的四点满足式(4)和式(5):
|
| 图 4 生成体素模型的原理示意图 Fig. 4 Diagram of the Principle of Generating Voxel Model |
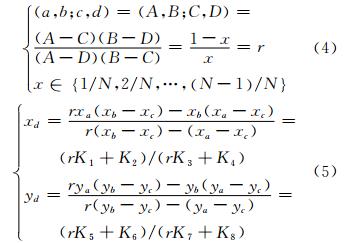
其中,r代表交比,已知一条直线上三个点的坐标值后,可以根据式(5)计算该直线上任意点的像点坐标;K1~K8为该直线的系数。由于体素的顶点位于规则格网点上,沿x方向的每一条直线的起点、终点和中点与直线上其他点组成的四点的交比r可以事先计算好,利用式(5)计算像点坐标比利用式(1)的计算量小一半以上。
2) 基于三维种子填充(flood fill)技术的体素模型快速提取。考虑三维空间内的任意一点(X,Y,Z),如果它在任何一张高斯平滑后(图 3(c))的分割影像 i上的像点(xi,yi)处的灰度值Gi(xi,yi) 小于给定的阈值(128),则它位于物体外部(OUT),否则位于物体内部(IN)。
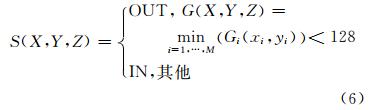
对于一个体素,若8个顶点中既存在OUT属性的顶点,又存在IN属性的顶点,则该体素与物体表面“相交”,称为ON体素,如图 4(b)所示。这种判断方法并不严密,如图 4(c)中标记“*”的格子,这种误差与体素的分辨率有关,当使用八叉树方法时,由于上层体素分辨率低,容易产生误差并会向下层传递,使用本文种子填充方法则不存在误差传递的问题。对于体素的12条边,若某条边的两个顶点分别具有OUT属性和IN属性,则该边与物体表面“相交”,称为交叉边(图 4(b)中水平的四条边)。根据以上定义,有如下推论: ① 与ON体素的一条交叉边相邻的3个体素也是ON体素; ② ON体素的18-邻域(26-邻域减去8个顶点相邻的)的体素中必有ON体素。
综上所述,基于三维种子填充算法的流程如下:
1) 建立一张N×N×N×1 bit的属性表(记录体素是否已被填充),一个待遍历的体素队列和一个ON体素链表。
2) 沿一条直线搜索到第一个ON体素,修改属性表为已填充,并把它加入到队列。
3) 从队列中取出一个体素,加入到链表,并遍历与其交叉边相邻的体素(必为ON体素),如果属性表为未填充,则修改为已填充,并加入到队列,重复这一步骤直至队列为空,此时链表中的体素就是所有ON体素的集合。
图 4(c)展示了一个二维的种子填充过程,其中的数字为填充顺序,ABC列对应于图 4(a)中的ABC点,标记“*”的格子是由于体素的分辨率不足导致的误差。相对于八叉树算法,三维种子填充算法的优点是不存在冗余计算,缺点是当场景中存在两个以上的物体时,由于两个物体之间是不连通的,将只能得到一个物体,八叉树算法则不受连通性影响。三维种子填充算法的时间复杂度是 O(M×N2),属性表的空间复杂度是O(N3),队列的空间复杂度是O(N),链表的空间复杂度是O(N2)。
1.4 生成网格及优化
从体素到网格,Lorensen[30]提出了移动立方体(marching cubes,MC)方法,根据体素8个顶点属性值的不同可以分为256种情况,考虑到立方体的对称性,Lorensen将其归结为15种情况,对于每一种情况,手动指定一种构建三角网格的方法,记录为查找表(图 4(b)是其中一种情况)。由于15种情况中的7种存在多义性问题,Chernyaev[31]将其扩展成了33种情况,并提供了一个增强的查找表。
本文使用MC算法由体素模型生成三角网模型,无论是在曲率较大的区域,还是在相对平坦区域,三角形的大小和数量都是均匀的,而我们希望得到的模型是在曲率较大的区域,三角形具有较小的面积和较多的数量,在相对平坦的区域,三角形具有较大的面积和较少的数量,因此本文进一步对三角网模型进行简化[32]。
2 实验结果与分析
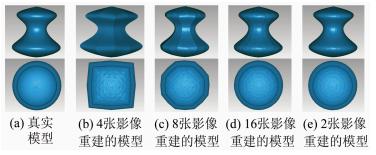
为了验证基于轮廓线的三维重建方法所能达到的理论精度,以及不同视角照片的数量与模型精度的关系,设计如下模拟实验。使用3ds max软件设计一个哑铃状的模型(图 5(a)),既含有凸面,又含有马鞍面,模型尺寸为1 000 mm×1 000 mm×1 100 mm。设计虚拟相机的尺寸为2 000像素×2 000像素,主距为4 000像素,拍摄距离为5 000 mm,绕物体轴线旋转一周模拟拍摄32张影像,分别使用其中的4、8、16、32张影像做基于轮廓线的三维重建,得到的模型如图 5所示。各个模型与真实模型的误差如表 1所示,最大误差是指模型上一点到真实模型上最近点的距离的最大值,平均误差是指所有误差的几何平均数,相对精度是指平均误差与模型尺寸(1 000 mm)的比值,相邻行精度的倍数关系反映了影像数量增 加一倍对模型精度的影响。从表 1中数据可以看出,模型的精度随着影像数量的增加而提高,但模型精度提高的速度渐缓,如最后一行影像数增加到原来的2倍,精度只增加到原来的1.6倍,因此适当地选择影像数量可以均衡模型的质量和工作量。
|
| 图 5 三维模型的正视图和俯视图 Fig. 5 Front View and Top View of 3D Models |
| 影像数/张 | 最大误差/mm | 平均误差/mm | 相对精度 | 相邻行精度倍数关系 |
| 4 | 90.18 | 25.10 | 1/40 | - |
| 8 | 33.97 | 4.57 | 1/219 | 5.5 |
| 16 | 9.19 | 1.20 | 1/833 | 3.8 |
| 32 | 3.18 | 0.75 | 1/1 333 | 1.6 |
为了验证本文方法的有效性,将一个陶瓷材质的水牛实物放在一张摊开的报纸上,用手机(华为T8833)从各个不同的角度拍摄32张影像(图 6(a)),影像尺寸为2 048像素×1 228像素,拍摄距离为300~600 mm,使用SFM方法计算出内外方位元素,由于自动对焦,影像的主距为1 990~2 100像素,影像的位置和姿态如图 6(b)所示。为了便于比较,用结构光扫描仪对水牛实物进行扫描,获取一个精度为0.03 mm的模型作为参考模型(图 7(a)),参考模型的尺寸为90 mm×46 mm×48 mm。

|
| 图 6 多视影像和其拍摄时的位置与姿态 Fig. 6 Multi-view Images and Their Shooting Position and Orientation |
|
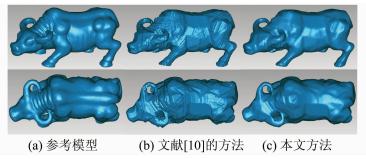
| 图 7 三种方法重建的水牛模型的正视图和俯视图 Fig. 7 Front View and Top View of Buffalo Models Reconstructed by Three Methods |
在每张影像上用§1.2的方法提取出轮廓线,然后分别用文献[10]的方法和本文§1.3、§1.4的方法生成模型,如图 7(b)、7(c)所示。可以看出,在物体的凸面、马鞍面部分(腿部、头部等)有较为接近参考模型的形状,而物体的凹面部分(尾巴等)没有反映出真实形状。另外,本文方法生成的模型更光滑,这是受轮廓线高斯平滑和三维模型简化的影响。由于扫描仪的坐标系和SFM的坐标系比例尺不一致,故使用绝对定向将后者统一到扫描仪的坐标系中,这样可以将扫描模型作为真值进行比较,结果见表 2,其中相对精度指平均误差相对于模型尺寸(90 mm)的比值。从表 2可以看出,本文方法与现有同类方法的精度相当,效率有所提高。方法的效率可以反映其计算量的大小,在手机、平板电脑等便携式计算终端逐渐普及的今天,将三维重建方法做到便携式设备中是未来发展的方向,而计算量越小,意味着便携式设备可以工作更长的时间。
真实物体实验的结果并没有达到模拟实验中同等数量影像(32张)的相对精度,这是由于真实物体的形状复杂,一方面存在“凹面”等不能够被基于轮廓线的方法所重建的区域;另一方面,影像的姿态分布较为分散,而模拟实验中的影像是分布在一个圆环上的,因此同等数量的影像(32张)其效果是不同的。另外,真实影像的背景复杂,在提取轮廓线时也会存在一定的误差。
本文提出了一种基于轮廓线的便捷式小型物体三维重建方法,该方法不受时间、场景、光照、材质和辅助设备的限制,仅需少量人工干预就可快 速生成三维模型,用于三维展示等目的。针对展示的目的和方便快捷的要求,本文重点解决了方便快速地获取方位元素、自动提取轮廓线、快速体素算法等问题,与现有的同类方法相比,计算量更少,更适合在便携式设备中实现。本文方法及同类方法的缺点是不能对物体的“凹面”部分进行重建,但其恢复物体三维模型的轮廓与影像相一致,足以满足普通个人的视觉需要。本文方法仅考虑了物体整体的外轮廓线信息,是物体与背景 的交界,然而物体本身也可能存在自遮挡现象,自遮挡会产生断裂线,是物体一部分与另一部分的交界,断裂线也是一种与物体材质无关的特征,今后将进一步研究融合轮廓线和断裂线信息的三维重建方法。
| [1] | Xu Gang. 3D Modeling from 2D Images[M]. Zheng Shunyi. Wuhan:Wuhan University Press, 2006(徐刚. 由2维影像建立3维模型[M]. 郑顺义. 武汉:武汉大学出版社, 2006) |
| [2] | Seitz S M, Curless B, Diebel J, et al. A Comparison and Evaluation of Multi-view Stereo Reconstruction Algorithms[C].Computer Vision and Pattern Recognition, 2006 IEEE Computer Society Conference on, New York, USA, 2006 |
| [3] | Hirschmuller H. Stereo Processing by Semiglobal Matching and Mutual Information[J]. Pattern Analysis and Machine Intelligence, IEEE Transactions on, 2008, 30(2):328-341 |
| [4] | Furukawa Y, Ponce J. Accurate, Dense, and Robust Multiview Stereopsis[J]. Pattern Analysis and Machine Intelligence, IEEE Transactions on, 2010, 32(8):1 362-1 376 |
| [5] | Sakai S, Ito K, Aoki T, et al. An Efficient Image Matching Method for Multi-view Stereo[M]. Berlin, Heidelberg:Springer, 2013:283-296 |
| [6] | Baumgart B G. Geometric Modeling for Computer Vision[R]. Technical Report AIM 2249, Dept of Computer Science, Stanford Univ, 1974 |
| [7] | Laurentini A. The Visual Hull Concept for Silhouette-based Image Understanding[J]. Pattern Analysis and Machine Intelligence, IEEE Transactions on, 1994, 16(2):150-162 |
| [8] | Matusik W, Pfister H, Ngan A, et al. Image-based 3D Photography Using Opacity Hulls[J]. ACM Transactions on Graphics (TOG), 2002, 21(3):427-437 |
| [9] | Sinha S N, Pollefeys M. Visual-hull Reconstruction from Uncalibrated and Unsynchronized Video Streams[C]. 3D Data Processing, Visualization and Transmission, The 2nd International Symposium on, IEEE, Thessaloniki, Greece, 2004 |
| [10] | Yemez Y, Schmitt F. 3D Reconstruction of Real Objects with High Resolution Shape and Texture[J]. Image and Vision Computing, 2004, 22(13):1 137-1 153 |
| [11] | Lazebnik S, Furukawa Y, Ponce J. Projective Visual Hulls[J]. International Journal of Computer Vision, 2007, 74(2):137-165 |
| [12] | Furukawa Y, Ponce J. Carved Visual Hulls for Image-based Modeling[J]. International Journal of Computer Vision, 2009, 81(1):53-67 |
| [13] | Cao Yu, Chen Xiuhong. 3D Reconstruction Method Based on Image Silhouette[J]. Computer Engineering and Applications, 2012, 48(6):205-208(曹煜, 陈秀宏. 基于图像轮廓的三维重建方法[J]. 计算机工程与应用, 2012, 48(6):205-208) |
| [14] | Liang C, Wong K Y K. 3D Reconstruction Using Silhouettes from Unordered Viewpoints[J]. Image and Vision Computing, 2010, 28(4):579-589 |
| [15] | DÍaz-Más L, Muoz-Salinas R, Madrid-Cuevas F J, et al. Shape from Silhouette Using Dempster-Shafer Theory[J]. Pattern Recognition, 2010, 43(6):2 119-2 131 |
| [16] | Haro G. Shape from Silhouette Consensus[J]. Pattern Recognition, 2012, 45(9):3 231-3 244 |
| [17] | Xia D, Li D, Li Q, et al. A Novel Approach for Computing Exact Visual Hull from Silhouettes[J]. Optik-International Journal for Light and Electron Optics, 2011, 122(24):2 220-2 226 |
| [18] | Muoz-Salinas R, Yeguas-Bolivar E, DÍaz-Más L, et al. Shape from Pairwise Silhouettes for Plan-view Map Generation[J]. Image and Vision Computing, 2012, 30(2):122-133 |
| [19] | Wallach H, óconnell D N. The Kinetic Depth Effect[J]. Journal of Experimental Psychology, 1953, 45(4):205-217 |
| [20] | Ullman S. The Interpretation of Structure from Motion[J]. Proceedings of the Royal Society of London:Series B, Biological Sciences, 1979, 203(1 153):405-426 |
| [21] | Snavely N, Seitz S M, Szeliski R. Skeletal Graphs for Efficient Structure from Motion[C]. CVPR, Anchorage, AK, USA, 2008 |
| [22] | Triggs B, McLauchlan P F, Hartley R I, et al. Bundle Adjustment—A Modern Synthesis[M]. Berlin, Heidelberg:Springer, 2000:298-372 |
| [23] | Lourakis M I A, Argyros A A. SBA:A Software Package for Generic Sparse Bundle Adjustment[J]. ACM Transactions on Mathematical Software (TOMS), 2009, 36(1):1-30 |
| [24] | Boykov Y Y, Jolly M P. Interactive Graph Cuts for Optimal Boundary & Region Segmentation of Objects in ND Images[C]. Computer Vision, the 8th IEEE International Conference on, Vancouver, Canada, 2001 |
| [25] | Farin D, Pfeffer M, Effelsberg W. Corridor Scissors:A Semiautomatic Segmentation Tool Employing Minimum-cost Circular Paths[C]. Image Processing, 2004 International Conference on, Paris, France, 2004 |
| [26] | Schmidt F R, Toppe E, Cremers D. Efficient Planar Graph Cuts with Applications in Computer Vision[C]. Computer Vision and Pattern Recognition, IEEE Conference on, Miami, FL, USA, 2009 |
| [27] | Martin W N, Aggarwal J K. Volumetric Descriptions of Objects from Multiple Views[J]. Pattern Analysis and Machine Intelligence, IEEE Transactions on, 1983, 5(2):150-158 |
| [28] | Szeliski R. Rapid Octree Construction from Image Sequences[J]. CVGIP:Image Understanding, 1993, 58(1):23-32 |
| [29] | Tarini M, Callieri M, Montani C, et al. Marching Intersections:An Efficient Approach to Shape-from-Silhouette[C].VMV, Erlangen, Germany, 2002 |
| [30] | Lorensen W E, Cline H E. Marching Cubes:A High Resolution 3D Surface Construction Algorithm[J]. ACM Siggraph Computer Graphics, 1987, 21(4):163-169 |
| [31] | Chernyaev E V. Marching Cubes 33:Construction of Topologically Correct Isosurfaces[R]. Institute for High Energy Physics, Report CN/95-17, Moscow, Russia, 1995 |
| [32] | Cignoni P, Montani C, Scopigno R. A Comparison of Mesh Simplification Algorithms[J]. Computers & Graphics, 1998, 22(1):37-54 |
 2015, Vol. 40
2015, Vol. 40




