文章信息
- 郑肇葆, 潘励, 郑宏
- ZHENG Zhaobao, PAN Li, ZHENG Hong
- 中智逻辑图像分割方法的研究与分析
- Research and Analysis of Neutrosophic Logic Image Segmentation (NLIS) Method
- 武汉大学学报·信息科学版, 2015, 40(2): 143-146
- Geomatics and Information Science of Wuhan University, 2015, 40(2): 143-146
- http://dx.doi.org/10.13203/j.whugis20130586
-
文章历史
- 收稿日期:2013-10-22
2. 武汉大学电子信息学院, 湖北 武汉 430079
2. School of Electronic Information, Wuhan University, Wuhan 430079, China
图像分割是图像处理中最基础的问题,图像分割的质量直接影响到后续的图像分类、图像解译以及模式识别等工作。如何提高图像分割的质量,已经引起有关方面的注意。在客观世界中,不同类别的影像之间可能存在一定的重叠,采用“一刀切”的办法不一定能将图像上的两个类别划分清楚。在实际情况中,难以确定图像上的一个目标属于某个类别,而不是其他类别的成员,由此引出模糊聚类的概念[1]。笔者曾应用模糊逻辑进行了图像分割的尝试,取得了一定的效果[2]。在近十多年中,不少学者针对模糊逻辑的不足作了进一步扩充,提出了中智逻辑(neutrosophic logic,NL)方法[3, 4]。中智逻辑不仅是研究模糊逻辑中一个目标属于类别A的模糊想法是“真”还是“假”的问题,而且还研究在“真”与“假”之间存在一个连续的中立区,在中立区中,目标的归属应为类别A还是B,这是个似是而非的问题。由此可见,中智逻辑考虑到的情况更接近客观真实的情况。为此,本文介绍了应用中智逻辑进行图像分割(NL image segmentation,NLIS)的原理方法和实验结果。
1 中智逻辑图像分割的原理和方法 1.1 中智逻辑的基本概念[3]
中智逻辑讨论的是中智集中的问题,假定在空间 X中存在一个中智集A,中智集A由三个子集“真”(truth)(隶属度函数TA(x))、“不确定”(indeterminacy)(隶属度函数IA(x))和“假”(falsity)(隶属度函数FA(x))组成。TA(x)、IA(x)、FA(x)是]-0,1+[的标准或非标准子集[3, 4]。即

其中,-0=0-ε,1+=1+ε,“0”和“1”表示标准部分;“ε”表示非标准部分。[0, 1]就是正常情况下的闭区间表示,式(1)即为非标准分析中的表示形式。由于这一特点,在中智逻辑分析的问题中,对TA(x)、IA(x)和FA(x)三者之和的值没有限制,即
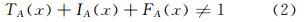
在图像分割问题中,如何将一个目标属于某一个类别为“真”、“假”或“不确定”的程度定量地表示出来,是至关重要的问题。
1.2 中智逻辑图像分割的数学模型
图像分割的目的是使具有相似特征性质的像元聚集在一起,使聚类内部的连通性、紧致性达到最大,而类间的连通性或紧致性达到最小[1]。根据这一要求,使用聚类区域中特征的均值和区域中像元的特征值来定义中智集的{真,不确定性,假}。
假定将一幅图像G划分为三个聚类区域G1、G2、G3,每 一个聚类区域的特征均值分别为Center1、Center2、Center3。在某个区域中,像元(i,j)属于该区域为“真”的程度由式(3)定义:
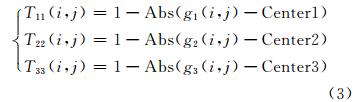
式中,T11(i,j)表示第一聚类区域中像元(i,j)属于第一区域为“真”的程度;T22(i,j)和T33(i,j)类似;g1(i,j)表示第一聚类区域中像元(i,j)的特征值(即灰度或分形维或能量);g2(i,j)、g3(i,j)类似; Center1、Center2、Center3分别为三个区域的特征均值;Abs()表示取计算结果的绝对值。
式(3)中,对于第一个公式,当g1(i,j)=Center1时,T11(i,j)=1。这个结果表明,在第一聚类区域中,像元(i,j)的特征值与该区域特征均值相等时,该像元属于第一聚类为“真”的值最大等于1。这个结果与把相同或相似性质的像元聚集在一起的要求是一致的。因此,用式(3)计算的结果作为中智集中“真”的程度度量是合理的。
“假”的定义如下:

中智集中不确定性的度量是这样考虑的:在区域1中,某像元(i,j)的不确定性是在这样的情况下发生的,即当某像元(i,j)的T11(i,j) 值较小时,表示该像元属于区域1为“真”的可能性很小,那么它属于区域2或区域3的可能性较大,在这样的情况下,把区域1中像元属于区域2或区域3为“真”的程度定义为区域1中像元的不确定性。即
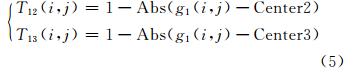
从式(5)可以看出,如果 T12(i,j)>T13(i,j),表明区域1中像元(i,j)的特征值接近区域2的特征均值Center2,该像元应离开区域1进入区域2中;否则,区域1中像元(i,j)应进入区域3中。由此,区域1中像元(i,j)的不确定性I11(i,j)由两部分组成:

类似地,区域2、区域3中像元(i,j)的不确定性为:

式(7)、式(8)中的符号与前面的定义相似。
式(3)~式(8)便是中智集中{T(i,j),I(i,j),F(i,j)}定量计算的数学模型。
1.3 中智逻辑法图像分割的主要过程
1) 将一幅图像初步划分为三个区域,利用图像的分形维特征值[5]构建直方图,根据直方图将图像划分成三个像元数近似相等的初始分割区域。
2) 利用式(3)分别计算出各区域中每个像 元(i,j)的“真”,即T11(i,j)、T22(i,j)、T33(i,j)。
3) 利用式(4)分别计算出各区域中每个像元(i,j)的“假”,即F11(i,j)、F22(i,j)、F33(i,j)。
4) 利用式(5)~式(8)分别计算出各区域中每个像元(i,j)的“不确定性”,即I11(i,j)、I22(i,j)、I33(i,j)。
5) 确定各区域中由于Tkk(i,j)值(k=1,2,3)较小(即为“真”的程度偏低)要离开各自区域的阈值。根据在模糊逻辑图像分割中的经验,采用隶属度值小于等于0.45作为离开各自区域的阈值[2]。在中智逻辑中,Tkk(i,j)的最大、最小值很少达到1和0,为此,采用更切合实际的阈值计算方法。

式中,Th1表示区域1像元离开本区域的阈值;t11min表示区域1中T11(i,j)的最小值;t11max表示区域1中T11(i,j)的最大值;其他符号Th2、Th3、 t22max、t33max、t22min、t33min亦有类似的意义。
有了阈值Th1、Th2、Th3,就明确了哪些像元应离开相应的区域,可是究竟应当归并到哪个区域不明确。
6) 不确定性Ikk(i,j)的计算。以第1区域为例,由式(6)I11(i,j)=(T12(i,j),T13(i,j)),其中T12(i,j)说明区域1中的像元划归区域2为“真”的程度,T13(i,j)为区域1中的像元划归区域3为“真”的程度,根据两个数值的大小,就可以决定应归并的区域。若T12(i,j)>T13(i,j),则区域1中的像元应归并到区域2,否则归并到区域3。其他两个区域仿照上述情况执行。
7) 经过以上6个过程,三个初步划分区域中的像元进行了一次重新组合,将这一过程称之为完成一次演化的过程。对三个区域,用它们的特征值分别计算各自的标准差σ。
8) 转入过程2),开始新一轮的演化计算,直至三个区域的标准差值σ趋向稳定或达到规定的演化次数为止。
2 对中智逻辑图像分割的分析与思考
从NLIS的原理方法介绍中可以看到,该方法的特点是对中智集中的“真”、“不确定性”、“假”三个要素给出可以定量表示它们的数学模型,特别是“不确定性”数学模型,它给出一个像元(i,j)属于其他区域为“真”的程度,程度的大小为准备离开所在区域的像元指出了归并的方向,加快了分割演化的进程。表 1为 NLIS中演化过程的部分数据,其中,Iter为演化迭代次数;Center为聚类区域像元特征的均值;σ为聚类区域像元特征的标准差;N表示区域中非零像元的个数。
| Iter | Center1 | σ1 | N1 | Center2 | σ2 | N2 | Center3 | σ3 | N3 |
| 0 | 1.447 7 | 6.812 9 | 4 186 | 1.562 4 | 1.905 6 | 2 319 | 1.643 2 | 3.550 1 | 1 958 |
| 3 | 1.460 0 | 6.532 2 | 4 668 | 1.592 9 | 7.600 8 | 2 365 | 1.621 0 | 2.637 4 | 1 430 |
| 5 | 1.460 0 | 6.532 2 | 4 668 | 1.599 2 | 7.138 3 | 2 923 | 1.617 8 | 1.644 3 | 872 |
| 7 | 1.460 0 | 6.532 2 | 4 668 | 1.601 6 | 6.796 6 | 3 301 | 1.616 6 | 0.579 | 494 |
| 9 | 1.460 0 | 6.532 2 | 4 668 | 1.602 9 | 6.490 4 | 3 640 | 1.616 7 | 0.168 | 155 |
| 11 | 1.460 0 | 6.532 2 | 4 668 | 1.603 3 | 6.407 0 | 3 740 | 1.616 6 | 0.058 | 55 |
| 13 | 1.460 0 | 6.532 2 | 4 668 | 1.603 5 | 6.372 9 | 3 782 | 1.616 6 | 0.019 | 13 |
| 15 | 1.460 0 | 6.532 2 | 4 668 | 1.603 5 | 6.364 8 | 3 792 | 1.616 7 | 0.001 | 3 |
从表 1中数据可有以下结论。
1) 只需15次演化迭代就完成中智逻辑图像分割的演化计算,三个区域的标准差 σ1、σ2、σ3 逐渐减小,且趋向稳定。这种情况与模糊逻辑图像分割(fuzzy logic image segmentation,FLIS)[2]相比,迭代次数减小一半(FLIS需要迭代35次)。
2) 从表 1中每个区域的非零像元数量 N1、N2、N3在演化迭代过程中的变化可以看出,第3个区域的N3越来越小,到第15次迭代后,第3个区域只剩下3个像元,即N3=3。 这是因为随着演化过程的进展,第2、3区域的特征均值越来越接近,对于Iter=15而言,Center2=1.603 5,Center3=1.616 7。这样的趋势说明,通过中智逻辑图像分割演化,将初始的三个划分区域变成了两个区域,给分割后图像的后处理带来了方便。
3) 从研究中认识到,利用中智逻辑解决具体问题时,确定中智集中“真”、“不确定性”、“假”的数学模型至关重要,不合理的数学模型不能给出正确的结果。目前有关中智逻辑的应用文章不少,但是给出定量数学模型的很少。如尝试将文献[6]中解决去图像噪声的中智集定量模型用于图像分割就行不通。
3 实验与分析
为了验证本文提出的用于图像分割的中智集中“真”、“不确定性”、“假”的数学模型表示的正确性,本文使用了已有的图像分割方法采用的三幅航空影像(100像素×100像素),如图 1所示,便于对比分析[2]。同时,本文对每个像元的分形维、能量和灰度值同时使用作为像元的综合特征也进行了NLIS实验,有关使用综合特征的细节参见文献[7]。为了作出定量评价,在Photoshop环境下,分别在三幅图像分割区域的边界上量测60~70个点的(i,j)值作为理论值,以便与实际分割的量测值进行比较,给出分割质量。

|
| 图 1 三幅原始图像 Fig. 1 Three Original Images |
由实验结果得到以下结论:
1) 中智逻辑图像分割(NLIS)的精度优于模糊逻辑图像分割(FLIS)的精度。从表 1中可见,NLIS法的精度高于FLIS法,特别是利用综合特征时。
2) 使用综合特征时,NLIS方法的分割精度明显高于使用单特征的分割精度。从表 2中数据的对比完全证明了这一点。从单特征图 2(a)、2(b)、2(c)与综合特征图 2(d)、2(e)、2(f)的对比可以看出,使用综合特征分割(对照图 1)图像的完整性优于单特征的。
| NLIS | FLIS | |||
| 单特征 | 综合特征 | 单特征 | 综合特征 | |
| 图1(a)53点 | 1.04 | 0.90 | 1.21 | 1.09 |
| 图1(b)68点 | 0.85 | 0.79 | 0.80 | 0.80 |
| 图1(c)63点 | 0.98 | 0.85 | 1.13 | 0.96 |

|
| 图 2 三幅航空影像NLIS的结果图 Fig. 2 NLIS Figure Results of Three Aerial Images |
从以上两点可以证明,本文提出的用于图像分割的中智集中三个要素“真”、“不确定性”、“假”的数学模型是正确的,新图像分割方法是有效的。
| [1] | Kashan A H, Rezaee B, Karimiyan S. An Efficient Approach for Unsupervised Fuzzy Clustering Based] Grouping Evolution Strategies[J]. Pattern Recognition, 2013, 46:1 240-1 254 |
| [2] | Zheng Zhaobao, Pan Li, Zheng Hong.Image Segmentation Based on Fuzzy Logic Methods[J]. Geomatics and Information Science of Wuhan University, 2014, 39(4):397-400(郑肇葆, 潘励, 郑宏.应用模糊逻辑图像分割方法的分析与研究[J]. 武汉大学学报·信息科学版, 2014, 39(4):397-400) |
| [3] | Smarandache F. Neutrosophic Set—A Generalization of the Intuitionistic Fuzzy Set[C]. 2006 IEEE International Conference on Granular Computing, Atlanta, USA, 2006 |
| [4] | Smarandache F. Neutrosophic Logic—A Generalization of the Intuitionistic Fuzzy Logic[C]. The 3rd Conference of the Eurpean Society for Fuzzy Logic and Technology, Zittan, Germany, 2013 |
| [5] | Zheng Zhaobao, Huang Guilan.Using Least Square Method for Texture Classification of Aerial Image and Analysing Some Relative Problems[J]. Acta Geodaetica et Cartographica Sinica, 1996, 25(2):21-26(郑肇葆, 黄桂兰.航空影像纹理分类的最小二乘法和问题的分析[J].测绘学报, 1996, 25(2):21-26) |
| [6] | Cheng H D, Guo Y H. A New Neutrosophic Approach to Image Thresholding[J]. New Math and Nat Computation, 2008, 4(3):291-308 |
| [7] | Zheng Zhaobao.Application of Biogeography-Based Optimigation to Image Segmentation [J]. Geomatics and Information Science of Wuhan University, 2011, 36(8):932-935(郑肇葆. 生物地理学优化(BBO)在图像分割中的应用[J]. 武汉大学学报·信息科学版, 2011, 36(8):932-935) |
 2015, Vol. 40
2015, Vol. 40


